基于煤岩割理正交各向异性性质的低渗透煤层压力数值模拟研究

王保辉, 闫相祯

(1.潍坊学院 建筑工程学院, 山东 潍坊 261061；2.河南大学 环境与规划学院， 河南 开封 475004；2.中国石油大学(华东) 储运与土木工程学院, 山东 青岛 266555)

0 引言

煤层是一种由割理和基岩煤块组成的双重孔隙介质，面割理与端割理的存在造成煤岩割理渗透率正交各向异性，严重影响煤层气抽放效果[1-3].近年来，随着煤层气开发深度和规模的加大，煤岩渗透率正交各向异性性质日益引发关注.2012年CHEN等[4]针对煤层渗透率正交各向异性对四分支和羽状井优化设计的影响开展研究，分析了四分支和羽状井的最优布井方位；同年黄学满[5]通过对煤结构异性对瓦斯渗透特性影响开展实验研究，分析了平行层理方向和垂直层理方向上的瓦斯渗透特性差异；2014年任飞等[6]通过试验对比分析了鄂尔多斯盆地老坑口矿井煤岩在增压过程和降压过程中不同割理方向煤岩应力敏感性差异；2017赵宇等[7]采用自主研发的煤岩三轴吸附解吸渗流试验系统开展煤体在不同围压和瓦斯压力下，吸附气体后煤样的面割理、端割理、垂直层理方向上的渗透率，对比分析煤体渗透率各向异性差异.

煤层气排采实质上是煤储层压力的传播过程[8].开展排采初期储层压降传播规律的研究对于煤层气开采和煤矿瓦斯治理具有重要的现实意义.近年来，众多学者对煤层压降传播规律的研究已经取得了一些成果，例如：2014年葛静涛等[9]采用古典隐式差分法求解煤层气平面径向一维渗流方程式，给出储层压力随排采时间的变化规律；2015年吕志强[10]对国内某地煤层气开采工程进行流固耦合数值模拟分析，分析瓦斯渗流过程孔隙流体压力变化规律；2016年张涛和王龙军[11]建立弹性多孔介质单相可压缩气体不稳定渗流的基本微分方程模型，得出了渗流过程中的压力分布关系式.以上这些学者的研究均丰富和发展了煤层气渗流理论,为本文工作的开展提供了参考和借鉴.然而上述研究并未考虑煤岩渗透率正交各向异性性质，而考虑耦合作用下煤岩割理渗透率正交各向异性性质对煤层压力和解吸半径影响的研究较为少见.

鉴于此，笔者基于煤岩割理正交各向异性物理性质，根据达西渗流定律、质量守恒定律和多孔介质弹性理论，建立了基于煤岩割理正交各向异性性质的煤层气水固三相耦合渗流模型，利用此模型分析了煤层气排采过程中压力和解吸半径分布规律，讨论割理参数对煤层压力的影响规律.

1 低渗透煤层气水固三相耦合模型的建立

1.1 煤岩应力场本构方程

假设煤层为各向同性材料且发生弹性小变形，由孔隙弹性力学可知固体相位移方程为：

(1)

1.2 煤层气水固三相耦合渗流场方程

1)煤层气、水两相渗流的连续性方程

假设煤储层中气、水两相流体在割理系统中的流动遵循Darcy渗流，并考虑渗流过程中重力、毛管力的影响，且煤储层内气、水的运移过程是等温的，则由质量守恒原理可得煤岩割理系统中渗流连续性方程为：

气相连续性方程：

(2)

水相连续性方程：

(3)

固相连续性方程：

(4)

式中：Sw、Sg分别为水、气相的饱和度；φ为裂隙的孔隙度；qm为质量源，kg/m3·s；qg、qw分别为井点所在网格单位体积储层的产气量和产水量，kg/m3·s.

2)煤层气水固三相耦合渗流方程

在三维空间、各向异性介质、考虑重力的影响下，Darcy定律推广形式为：

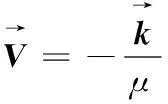
(5)

由于煤岩中面割理和端割理一般以相互垂直的两组出现，则在新坐标系下的渗透张量则变成为：

(6)

式中:Kf为流体沿着面割理方向的渗透率，μm2；Kb为流体沿着端割理方向的渗透率，μm2；Kz为流体沿着坐标轴z方向的渗透率，μm2.

将式(5)、式(6)分别代入式(2)并根据式(4)经过化简整理可得煤层气渗流方程为：

(7)

同理可得水相渗流方程：

(8)

其中

式(7)和式(8)即为煤层气水固三相耦合渗流方程.

3)辅助方程

① 毛管压力方程

Pc=Pg-Pw.

(9)

② 渗透率方程[12]

(10)

以上方程构成了考虑煤岩变形及割理正交各向异性性质的煤层气水固三相流固耦合数学模型，方程组封闭，加上边界和初始条件即可求定解.

2 实例分析及讨论

2.1 煤层气开采过程中压力分布

基于上述模型，对沁水盆地煤层井气排采过程中煤层压力开展数值模拟.根据沁水盆地煤层特点选取100 m×200 m×70 m区域作为计算分析对象，在单井控制范围外均为定压和定饱和度边界.煤层气、水渗流的数值模拟基本参数见表1，数值模拟结果见图1—图3.

表1 煤储层模拟参数Tab.1 Parameter values of coal seam

图1为耦合与非耦合条件下煤层压力分布曲线，可以看出，相同的排采制度，非耦合条件下的压力下降范围较耦合条件下压力降低范围要大.这是由于随着煤层中孔隙压力不断降低，煤岩受到进一步的压缩，孔隙体积进一步减小，最终导致渗透率降低的缘故.而非耦合模型中是将渗透率视为常数来处理的，没有考虑多孔介质变形对煤层气藏物性参数的影响，因此压力降低范围偏大.另外，煤层经排水采气30 d后在井底附近形成压降漏斗，由于煤岩割理渗透率的正交各向异性性质，压降漏斗成椭圆形，漏斗的椭圆度随着割理渗透率正交各向异性系数的增加而增加.当井眼附近压降漏斗区域内的压力降到临界解吸压力以下，煤层气开始解吸，随着煤层中的压力降落漏斗不断扩大和加深，煤层解吸半径逐渐增大，解吸量逐渐增加.图2和图3为在一定排采制度下，煤层解吸半径随排采时间的分布曲线.由图可知，在一定的排采制度下，随着煤岩割理渗透率正交各向异性系数的增大，煤层面割理方向解吸半径呈非线性增长，而煤层端割理方向解吸半径逐渐减小；面割理方向最大解吸半径达69 m，端割理方向最大解吸半径达40 m.

图1 耦合与非耦合时煤层压力分布Fig. 1 Pressure distribution of the coupling model and non-coupling mode

图2 面割理方向解吸半径分布Fig. 2 The desorption radius distribution along the face cleat direction

图3 端割理方向解吸半径分布Fig. 3 The desorption radius distribution along the butt cleat direction

2.2 割理参数对煤层压力影响

为了研究煤岩割理参数对煤层压力的影响规律，利用本文模型对煤岩割理参数进行敏感性分析，结果见图4～图9.

图4和图5为割理渗透率正交各向异性系数对煤层压力分布影响曲线.可以看出，煤岩割理渗透率正交各向异性对煤层压力分布有重要影响.煤层水平距离60 ～140 m范围内，随着煤岩割理渗透率正交各向异性系数的增大，沿面割理方向煤层压力逐渐增大；煤层水平距离0 ～60 m和140 ～200 m范围内，沿面割理方向煤层压力逐渐减小.由图5可知，随着煤岩割理渗透率正交各向异性系数的增大，沿端割理方向煤层压力逐渐增加.

图4 渗透率正交各向异性系数与煤层面割理方向压力分布曲线Fig. 4 The pressure distribution along the face cleat direction

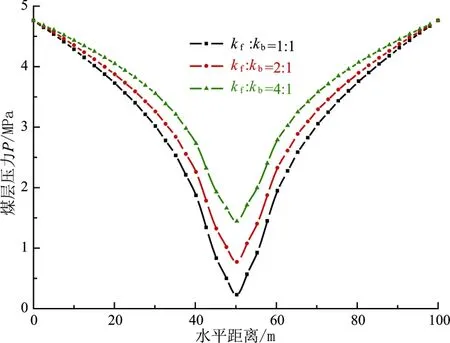
图5 渗透率正交各向异性系数与煤层端割理方向压力分布曲线Fig. 5 The pressure distribution along the butt cleat direction

图6和图7为割理密度对煤层压力分布影响曲线.从理论上讲，割理越发育越有利于渗透性的提高，割理是煤层中的主要裂隙系统，是渗透性预测的重要参数.可以看出，割理密度对渗透率的影响较大，割理密度越高，煤层渗透性越好.在定流量开采的条件下，割理密度越大，井眼附近压力恢复快，反之压力来不及恢复，压降漏斗大.

图6 割理密度与煤层面割理方向压力关系曲线Fig. 6 Curve of the cleat density and the pressure along the face cleat direction

图8和图9为割理宽度对煤层压力分布影响曲线，由图8可知，煤岩割理宽度对煤层压力分布有重要影响.在定流量开采和端割理宽度不变的条件下，沿煤层水平距离80 ～120 m范围内，面割理宽度越大，沿面割理方向压力降低越小；沿煤层水平距离0 ～80 m和120 ～200 m范围内，割理宽度越大，沿面割理方向压力降低越大.由图9可知，面割理宽度越大，煤层压力沿端割理方向越小.

图7 割理密度与煤层端割理方向压力关系曲线Fig. 7 Curve of the cleat density and the pressure along the butt cleat direction

图8 面割理宽度与煤层面割理压力方向关系曲线Fig. 8 Curve of the face cleat width and the pressure along the face cleat direction

图9 端割理宽度与煤层端割理方向压力关系曲线Fig. 9 Curve of the butt cleat width and the pressure along the butt cleat direction

3 结论

基于煤岩变形介质及割理正交各向异性性质，建立了反映煤层气、水两相渗流的流固耦合数学模型.利用该模型对沁水盆地煤层气井排采过程中煤层压力、解吸半径及割理参数对煤层压力的影响规律进行分析. 计算结果表明，非耦合模型比耦合模型的解吸面积要大；随着煤岩割理渗透率正交各向异性系数的增大，煤层面割理方向解吸半径逐渐增大，而煤层端割理方向解吸半径逐渐减小；沿面割理方向，随着割理渗透率正交各向异性系数和割理宽度的增加，煤层压力先增大后减小；沿端割理方向，煤层压力随着渗透率正交各向异性系数、割理密度和割理宽度的增大而增大.