热力交互作用下冻土路基融化沉降分析

房建宏，徐安花，姚晓亮，张 泽

(1.青海省交通科学研究院，青海 西宁 810008；2.中国科学院西北生态环境资源研究院 冻土工程国家重点实验室，甘肃 兰州 730000)

0 引言

20世纪80年代以来，我国在多年冻土区开展了广泛密集的工程建设，例如青藏公路、铁路、400 kV直流输变电线路和中俄输油管线等.随着这类冻土区重大工程建设的持续开展，一系列工程病害也随之出现，如冻土路基的沉陷、路面裂缝、塔基沉陷等.由于工程扰动所引起的多年冻土的持续退化是其主要诱因[1].冻土的持续退化会导致多年冻土的不断融化.对青藏公路和铁路的监测结果显示，冻土路基的大多病害主要来源于多年冻土层的融化[2, 3].伴随着冻土融化后孔隙水的不断排出，地基的固结沉降也随之发展.因此，在冻土地基的稳定性分析中融化沉降仍然是需要考虑的主要因素.针对冻土的融化沉降过程，研究者主要采用融化固结理论来描述其发展规律.MORGENSTERN和NIXON[4]、FORIERO和LADANYI[5]基于一维融化固结理论和融化边界经验公式得到了一维融化固结理论.这类理论能够描述简单热学和力学条件下冻土的融化固结行为，但对边界条件复杂的工程问题其适用性有限.SYKES等[6]基于BIOT小变形固结理论和热传导方程得到了适用于三维复杂边界条件的融化固结理论.在此基础上，QI等[7]使用显热熔法进一步完善了三维小变形理论.考虑到小变形理论在计算高含冰量土体融化时所产生过大误差，YAO等[8]使用基于现时构形的欧拉描述方法建立了三维大变形融化固结理论，并通过试验验证了其适用性.以上理论仅针对常温边界的情况，无法处理周期温度边界条件下的融化固结问题.QI等[9]针对具体工程问题，提出“等效固结时间”的概念，并研究了多年冻土路基的融化沉降规律.该方法仍然是对周期温度边界影响的一种近似.在具体计算时需要首先根据温度场的计算确定“等效固结时间”，极大地降低了计算效率，不利于高效工程计算.基于这样的考虑，WANG等[10]提出了一种能够直接考虑周期温度边界影响的数值模拟方法，并通过实测数据验证了其正确性.

本文将在大变形融化固结理论的基础上，建立适用于多构筑物共同作用下的冻土地基融化沉降数值模拟平台.通过分析不同路基间距条件下，公路和铁路路基对下覆土层热学和变形场的综合影响，为多年冻土地区构筑物密集修筑地区的施工选线以及病害防治提供合理化建议和技术支持.

1 控制方程及精度控制

冻土的融化固结计算实质是典型的热、力学和流体耦合计算[11]，即：在整个计算区域进行热学计算，同时在融化区域进行固结计算.在进行热学计算时，考虑到冻土的冰-水相变潜热对其比热容的影响，需要使用考虑冰水相变的热传导方程：

(1)

其中：T为温度，℃；hv为体积热源，W/m3；c为考虑冰水相变的比热容，J/kg·℃；λ为考虑冰水相变的导热系数，W/m·℃；r为介质密度，kg/m3；t为时间，s.

通过式(1)的热学计算可以得到计算区域的热学状态，根据热学状态在已融化区域使用固结理论来描述土骨架与流体的力学行为.这里对已融土体的应力应变关系采用线弹性模型进行描述，即：

(2)

介质中流体的流动使用达西定律来描述：

qi=-k(p/ρwgi-xj)′i,

职业礼仪是一个行业最基本的道德要求，是人们在交往的过程中表现的一种行为，包括仪表、仪态、着装礼仪、接待礼仪等，不同的场合礼仪要求也不同，礼仪就是一面镜子，能找出自己的美与丑，它蕴含着丰富的文化底蕴，是社会进步的体现，个人职场礼仪和职业形象的展现也是职场中竞争的关键元素。

(3)

其中：qi为流体的流速，m/s；k为介质渗透系数，m/s；ρw为流体密度，kg/m3；gi为重力加速度，m/s2.

流体质量守恒方程可以写为：

(4)

其中，qv为体积流源，1/s;ev为体积应变.

式(2)中杨氏模量(E)，可以用压缩模量Es进一步表示为：

(5)

考虑大变形的影响，式(2)中总应力率修正为：

(6)

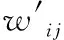
(7)

其中：Lc为计算网格单元的平均长度，m；cfl和cth分别为流体和热学计算的扩散系数，m2/s.在满足式(7)的基础上，流体和热学计算步长的选择应保证每个计算循环后其实际热学和流体计算时间相同，即：

dtth=Ndtfl,

(8)

式(8)表明在融化固结耦合计算中，每一次循环计算包括一次热学计算(式(1))，和N次流体计算(式(2)—(6)).

基于以上融化固结理论，本文所建立的多路基结构相互作用融化沉降数值模拟平台是在FLAC数值软件的基础上，基于热学、流体和力学计算模块进行二次开发所建立的.如前所述，冻土的融化沉降问题其实质是在实时变化的融化区域内进行固结计算，而现有的商用软件无法实现计算区域的实时变化.因而，本文所开发的数值平台是通过控制热学、流体和力学的计算流程，来实现在实时变化的融化区域内进行流体和力学(固结)计算.具体计算流程如下：

(1)首先使用式(1)进行一个时步(dtth)的热学场计算.

(2)根据温度场计算结果判断融化区域(温度高于0 ℃的区域)，并调用流体和力学计算模块(式(2)—(4))在融化区域进行N个时步(dtfl)的固结计算.

步骤(1)和步骤(2)的计算循环进行，直到达到目标计算时间.

2 工程算例

选取青藏高原唐古拉北坡某典型路基断面为研究对象.为了便于表述，取天然地表为原点，向下为正.层岩性分布如表1所示.路基几何模型如图1所示.公路路基高度为3 m,铁路路基高度为5 m，边坡坡度为1∶1.5，天然土层厚度为30 m.其中，公路路基为不采取任何保温措施的填土路基，铁路路基为采用主动降温功能的开放块碎石夹层路基，夹层厚度1.5 m.铁路路基顶端碎石道砟层厚0.4 m.为了研究铁路和公路相邻距离对下覆土层力学和变形场的影响，其坡脚之间的间距h采用三种不同的距离(5 m、 10 m和20 m).计算所需热学、力学参数如表2所示.其中热学参数根据《冻土物理学》得到[13].路基填土、粉质黏土、黏土和强风化泥岩的压缩模量根据朱元林等[14]中的相关参数获取.各土层的渗透系数根据QI等[7]和YAO等[11]获取.对于土体的排水条件，由于公路路面为透水性极低的沥青材料，因而设为不透水边界.公路路基边坡和天然地表为自由排水边界.由于铁路路基底面为孔隙较大的块碎石夹层，因而铁路路基底面也为自由排水边界.本文仅考虑路基在自重情况下的固结变形，土体重力作为体力施加于土体.

表1 路基断面地层岩性分布Tab. 1 Soil strata distribution

注：少冰冻土：i<10%；多冰冻土i:10%～20%；饱冰冻土i:30%～50%；含土冰层i>50%,i为体积含水量.

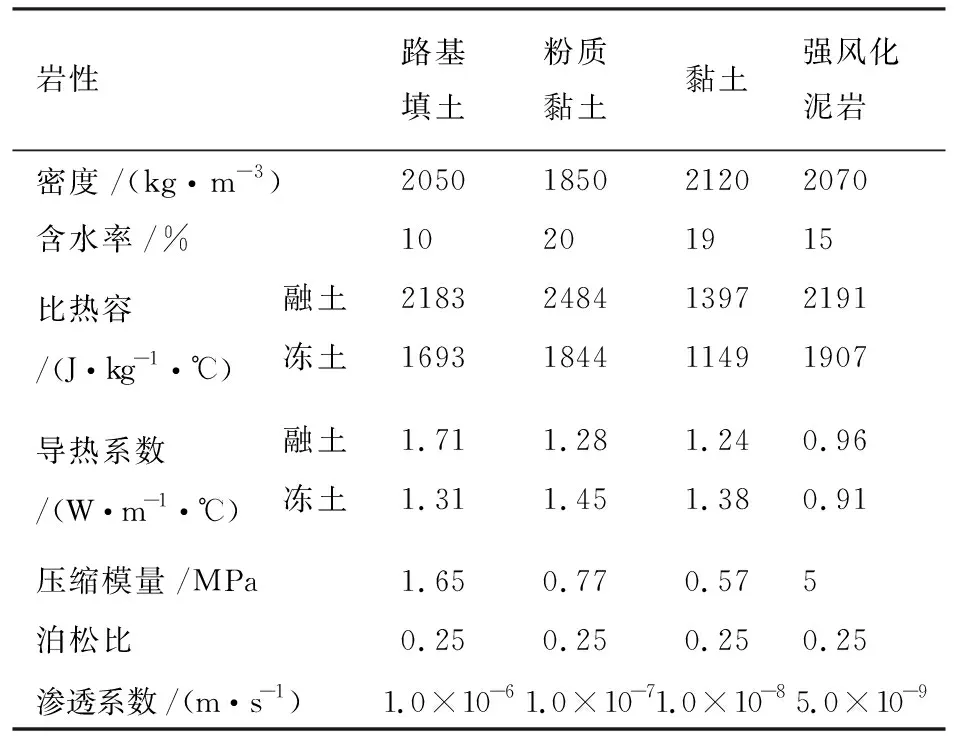
表2 各岩层热学力学参数Tab. 2 Thermal and mechanical parameters of soil strata

对于公路路基的温度边界，根据现场监测资料路基表面、路基边坡和天然地表温度均遵循正弦变化规律，即：

(9)

其中：T0为年平均温度，l为温度振幅，np为初始相位(本文中的算例取p/2)，a为地表温度年增温率(0.02 ℃/年).对于铁路路基边界温度，据赖远明等[15]的研究结果，铁路路基底面温度状况主要受控于具有降温效果的块碎石夹层.由于块碎石夹层中产生的强迫对流的影响，其底面处的温度处于-0.2 ℃附近基本保持不变，因此铁路路基底面设为-0.2 ℃恒定温度边界，其水平方向作用范围与路基顶面范围相同.公路路基不同边界处的温度振幅和平均温度如表3所示.天然土层的初始温度如图2所示.路基填土的初始温度取为5 ℃.模型(图1)下边界热流条件根据图2获取，具体为0.02 ℃/m.

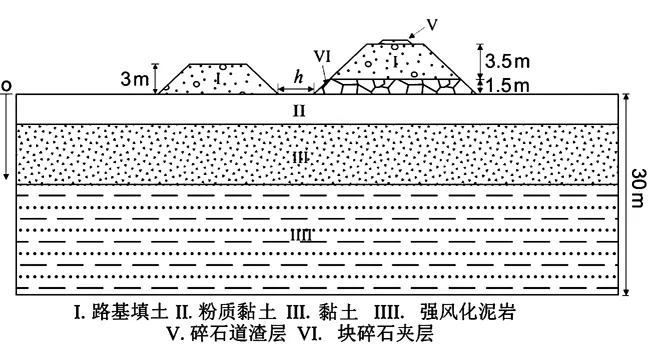
图1 公路和铁路路基模型示意图Fig. 1 Highway and railway embankment model sketch map

位置温度振幅 / ℃公路铁路年均温度 / ℃公路铁路路基表面13.1812.114.452.11路基边坡11.5211.752.241.75天然地表3.69-0.17

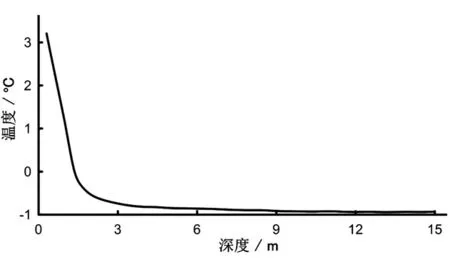
图2 天然土层初始温度Fig. 2 Natural soil initial temperature

3 结果与讨论

3.1 融化深度

图3为不同相邻间距条件下路基下多年冻土融化深度随时间的发展情况.从图中可以看出公路路基中心位置处融化深度最大，边坡次之,天然地表最浅.铁路下方融化深度分布规律与公路相反，即：边坡处最深而路基中心位置处最浅.这是由于两种路基不同的热学边界条件造成的.对于公路路基，由于其沥青路面相对于裸露的边坡具有较高的吸热性，因而公路路基中心位置下方融化深度发展较快，其融化盘呈现为下凹型；对于铁路路基，由于路基底面块碎石夹层主动降温的作用使得该处温度常年处于-0.2 ℃，因而路基中心位置处融化深度不会随时间产生明显变化.受边坡温度边界的影响，铁路路基边坡范围内的融化深度则随时间持续发展，从而形成铁路路基下方上凸型的融化盘.

随着时间的推移，公路和铁路路基下方融化盘持续扩大.在两种路基融化盘持续扩大的同时，公路路基右侧和铁路路基左侧的融化盘也呈现出从逐渐接近到相互重合的发展趋势(图3a和3b).对比不同路基间距融化盘的发展规律可以发现，两种路基融化盘重合的时间正比于路基的间距.对于间距5 m的情况，从图3a可以看出两种路基的融化盘在20年时基本重合；当间距增加到10 m时两种路基的融化盘在30年左右重合(图3b)，而对于间距20 m的情况,到第50年时两种路基的融化盘已经非常接近但并未重合(图3c).对比相同时间点不同间距融化盘的范围(以20年间距5和20 m为例(图3a和3c))还可以发现，两种路基融化盘重合后,其范围大于两种路基融化盘尚未重合的情况.这表明，两种相邻的路基结构之间会产生叠加放大的热学影响，即：融化盘重合后会加快融化深度的发展速度，这将进一步影响到路基在长期运营过程中其沉降变形的稳定性.

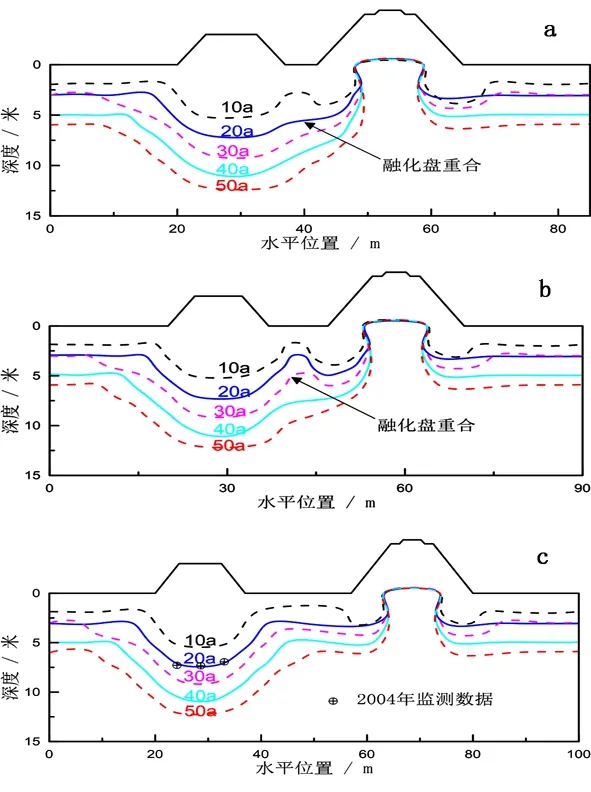
图3 不同间距冻土路基融化深度a.间距5 m; b.间距10 m; c. 间距20 m Fig. 3 Thaw depth of permafrost embankment at different horizontal space

3.2 沉降变形

图4为公路和铁路路基左右路肩和路基中心位置处沉降变形随时间的发展变化曲线.对于公路路基，从图4a—4c可以看出，公路路基中心处沉降发展较快而路肩位置较慢；与之相反，铁路路基路肩位置处沉降变形发展快于路基中心位置沉降.从3.1节可知，两种路基顶面不同位置处沉降的不同发展趋势主要取决于路基下方融化深度的发展趋势(图3).对比两种路基左右路肩处的沉降曲线(图4)可以发现，两个位置处的沉降在路基运营的最初阶段是基本重合的，当运营时间大于某一时间点时,公路路基右路肩处和铁路路基左路肩处的沉降开始加速发展.

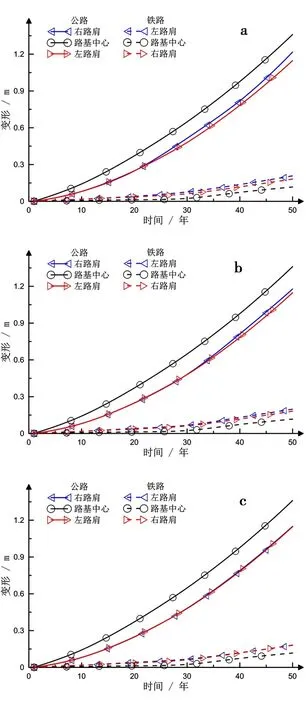
图4 不同间距冻土路基路面变形随时间发展关系曲线a.间距5 m; b.间距10 m; c. 间距20 m Fig. 4 Development curves of pavement deformation with time at different horizontal space

这一时间点与两个路基下方融化盘的重合时间一致(图3).以路基间距5 m的情况为例(图3a和4a)，在20年之前，两个路基下方的融化盘逐渐接近但并未重合.两个路基下方融化盘对应于各自路基中心位置是对称的，因而左右路肩沉降变形发展保持一致.20年后，随着两个路基下方融化盘重合后融化深度的加速发展，公路路基右路肩处和铁路路基左路肩处的沉降也随之快速发展.通过对不同时间和路基间距情况下路基沉降变形等值线图进一步直观地看出融化盘重合对沉降变形的影响.从图5可以看出，对于间距5 m的情况，在20年融化盘刚开始重合时(图3a)，两个路基的沉降变形等值线相对于各自路基中心位置是基本对称的(图5a).随着时间持续发展，融化深度持续扩大(图3a)，融化盘重合后对沉降变形的造成的影响持续增大.从第50年的沉降变形等值线分布情况可以看出(图5b)，两个路基的直线均出现了严重的不对称，且均倾向于两个路基间的中点方向；路基间距10 m的情况(图6)，路基沉降等值线的分布也呈现出相同的发展规律.对于间距较远的情况(20 m)(图7)，在运营的50年内，由于其融化盘没有产生交互影响，因而两个路基的沉降等值线均对称于各自路基中心位置(图7a和b).这表明随着相邻间距的增加，两种路基间的热学和力学场的相互叠加影响将逐渐减弱.

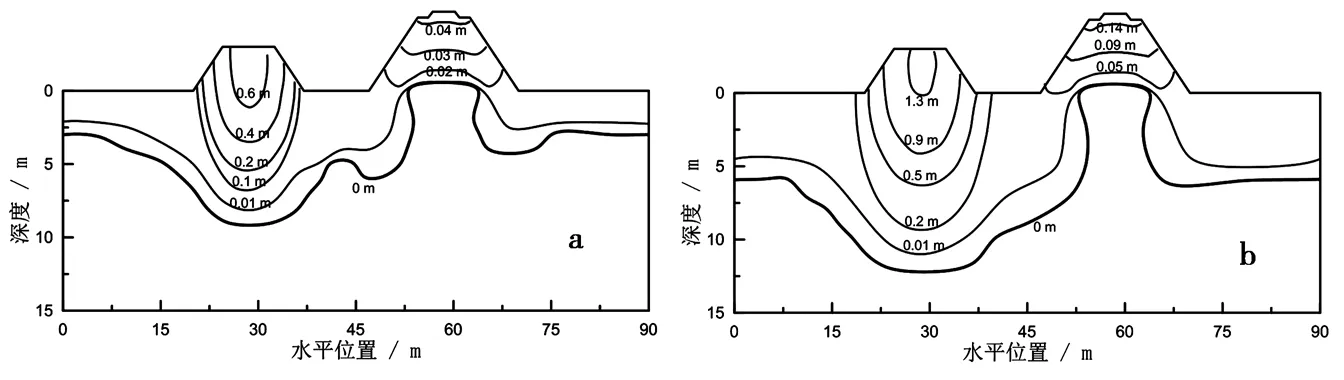
图6 间距10 m路基沉降变形等值线图(a. 20年， b. 50年 )Fig. 6 Settlement deformation contour lines for 10 m horizontal space

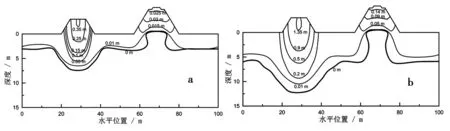
图7 间距20 m路基沉降变形等值线图(a. 20年， b. 50年 )Fig. 7 Settlement deformation contour lines for 20 m horizontal space

以上结果为不同间距条件下，两种路基融化深度、路面沉降以及沉降等值线随时间的发展变化的计算结果.下面将进一步结合路基融化深度和路面沉降的实测结果验证本文计算结果的正确性.从图4c可以看到，2004年不受铁路影响的公路路基融化深度的监测结果与第20年的计算结果基本一致.因此，可以将2004年以后的路面中心位置的沉降监测结果和20年以后的计算结果进行比较.图8为公路路面中心位置处3年左右的实测和计算沉降结果.从图中可以看到，实测和监测结果的发展趋势基本一致，即：随着时间的发展，路基融化沉降总体上呈线性发展趋势.实测结果略大于计算结果，这是由于本文的计算仅考虑了土体自重造成的沉降变形.而在实际工程中由于公路车辆荷载的影响，路基下覆融化土体还会发生额外的附加变形，因而计算结果略低于监测结果.总体来看，使用本文提出的融化固结数值计算方法,能够较为准确的预测和描述冻土路基的融化沉降发展规律，可以作为分析计算冻土区多构筑物热力交互影响的有效工具.

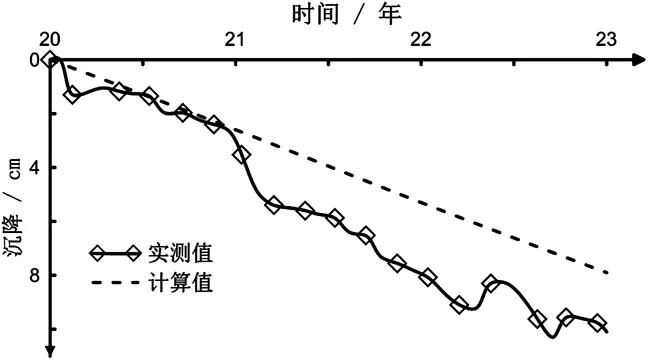
图8 公路路基中心位置处沉降Fig. 8 The settlement at center of highway embankment

上述分析表明，冻土路基长期融化沉降的稳定性取决于其热学状况.对于相邻修建的不同路基结构，过近的间距将引起不同路基结构下方热学状态的放大叠加影响，从而加速路基融化沉降的发展，进一步降低其稳定性.在采取适当措施保证冻土路基热学稳定性的基础上，不同构筑间还需保证足够的安全距离.对于本文研究的算例，建议设计运营时间为50年条件下不同路基结构间最小间距为20 m.

4 结论

本文基于大变形融化固结理论,建立了多构筑物共同作用的融化沉降数值模拟平台，在此基础上研究不同相邻间距条件下铁路和公路路基间热学和力学场的相互影响，得到以下结论：

1)铁路和公路路基下覆冻土层融化盘的重合时间正比于两种路基的相邻间距.当两种路基相邻距离过近时，路基融化盘的重合会加剧融化深度的发展，这将进一步加剧路基长期沉降的发展.

2)路基沉降的发展取决于其下覆冻土层融化盘的发展.对于相邻间距较近的情况，随着时间的推移，铁路和公路路基路肩位置处的沉降不对称性均持续发展.这主要是路基下方融化盘的不对称发展引起的.

3)对应于路肩位置处的沉降，路基下方变形场的不对称性也随着相邻间距的增大而逐渐降低.这表明随着路基相邻间距的增加，两种路基结构间的热学和力学场的相互叠加影响将逐渐减弱.对于本文的算例，建议设计运营时间为50年的路基结构其相邻间距应大于20 m.