多纤芯弹性光网络中虚拟网络映射模型及算法

宋俊辉, 谢 华, 高海龙

(1.信阳师范学院 计算机与信息技术学院, 河南 信阳 464000;2.信阳职业技术学院 检验学院, 河南 信阳 464000;3.中国人民解放军68128部队, 甘肃 武威 733200)

0 引言

随着大数据、云计算等新型业务的快速发展，导致现有光网络架构难以满足网络业务多样、动态和突发等需求.网络虚拟化应运而生，它可以灵活地为连接请求分配带宽，无需对传统网络架构进行很大改动就能获得较高的频谱利用率，满足用户的多样化需求.通过逻辑隔离的多个虚拟网络共享底层物理网络资源，可实现网络资源的弹性管理，加快网络新技术的开发与部署，有效地增加资源利用率[1,2].

近年来已经有越来越多的研究关注于弹性光网络的虚拟化，并对其进行了深入研究.网络虚拟化的难点在于如何设计高效的虚拟结点、链路的映射及频谱分配方案以达到某种预期的目的[3].为解决虚拟网络节点映射问题，文献[4]提出了一种整数线性规划模型和一种基于业务矩阵的映射算法以得到最优的方案.文献[5]研究了网络虚拟化环境下的跨域虚拟网络映射，分别提出了基于OWL及SWRL的资源匹配算法和基于遗传算法的虚拟网络划分算法.文献[6]根据虚拟网络带宽需求将物理网络抽象为多个分层辅助图，应用最短路径算法在分层辅助图上进行虚链路，提高链路映射效率，但是未考虑物理承载节点特性和链路负载对映射的影响.文献[7]建立了两个整数线性规划模型，并提出了基于贪心策略的虚拟网络映射算法，以减少最小化网络的最大占用频隙号.文献[8]利用节点介数中心性，将实时感知的网络状态作为选路因子，采用K最短路算法进行映射虚链路.由于该算法并未考虑链路频谱使用状态的影响而导致部分物理链路承载过重.

已有相关文献旨在最小化网络的能耗或网络最大占用频隙号等目标，然而频谱也是弹性光网络中的一种重要资源，因此本文研究了最小化网络中的占用资源数及最小化最大占用频隙号为目标的虚拟网络映射问题，建立了一个混合规划模型，并提出了一种有效的全局优化算法以得到最优的虚拟结点映射、虚拟链路映射及选路方案.

1 问题描述与建模

1.1 网络与业务描述

无向图G=(V,E)表示一个物理弹性光网络，其中V={v1,v2,…,vNv}表示物理弹性光网络中的结点集合，N是物理网络中结点的个数.对于每个物理结点vi(vi∈V),都有h(vi)个虚拟机.E={Lij|vi,vj∈V}表示物理网络中链路的集合，Lij是结点vi和结点vj之间的链路，NE是链路的条数.F={f1,f2,…,fNf}是一系列可用频隙，Nf是每个链路上可用频隙的个数，假设每个频隙具有相同的带宽Cfs.

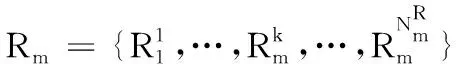
1.2 问题建模

本研究旨在为确定最优的节点映射、链路映射及频谱分配方案，以使得为所有业务请求分配频谱后所占用总的频隙最少.为此建立一个带有约束的全局优化模型，下面给出研究问题的数学模型.

目标函数：为所有业务请求分配频谱后所占用的频谱数最少且最大占用频隙号最小.目标函数可以表示为

(1)

虚拟结点映射满足的约束条件：(1)所有的虚拟节点必须映射到一个物理结点上；(2)同一个虚拟网中的虚拟结点不能映射到同一个物理结点上；(3)映射到同一个物理结点上的虚拟结点数不大于该物理结点上的虚拟机的数量.因此有：

研究手段：以错误分析理论为指导在整个学年的口译课上，对老师当堂布置的口译任务中学生出现的错误进行记录，同时对整个学年当中，学生课后口译录音作业中所出现的错误也进行了记录，最后分类、归纳、整理。

(2)

(3)

(4)

频谱分配满足约束条件：(a)业务请求只能占用联通原结点和宿结点所有通路中的一条路径；(b)业务在所占路径中的不同链路上具有相同的的起始频隙号；(c)一个业务请求必须占用若干个连续的频隙；(d)任意两个业务所占用的频谱无重叠.

(5)

(6)

(7)

(8)

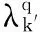
2 全局优化遗传算法

遗传算法在工程技术领域等实际应用问题中得到了广泛的应用，尤其是解决NP组合优化问题中更是表现出了其优良的性能[9].因此，本文设计了一种新的全局优化遗传算法来求解本文提出的最大化服务质量的可分任务调度模型.

2.1 编码与解码

采用首次适应策略(First Fit, FF)进行频谱分配，因此只需要对虚拟节点映射和选路进行编码.

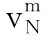
(9)

(10)

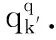
2.2 交叉与变异算子

交叉操作是遗传算法的主要进化手段，通过两两染色体基因交叉互换，繁殖两个新的子代个体，并将父代好的基因遗传至子代个体，产生的子代个体可能会优于父代个体.交叉操作保持了遗传算法种群个体的多样性和全局搜索能力.本文采用两点交叉方式生成新个体：随机生成两个整数j1和j2满足2≤j1≤j2≤N′(对选路个体进行交叉时2≤j1≤j2≤NR′)作为交叉点，将两个父代个体交叉点之间的基因进行交换，生成两个后代个体.

变异算子通过一定概率的基因变异，可以在一定程度上提高多样性，强化了算法搜索到最优解的能力.本文采用单点变异方式生成新个体：随机生成一个整数j1满足2≤j3≤N′(对选路个体进行交叉时2≤j3≤NR′)作为变异点，将个体在该点的基因位取反，产生新的后代个体.

2.3 不可行解可行化

由于物理结点vi(∀vi∈V)只有h(vi)个虚拟机，因此只能有不超过h(vi)个虚拟结点映射到物理结点vi上，然而在交叉变异过程中,会使得某些结点上映射的虚拟结点数超过其所拥有的虚拟机的数量,导致该虚拟结点映射个体成为一个不可行解，因此本文设计了一个可以将虚拟结点映射的不可行解进行可行化的可行化算子，如算法1所示.

算法1：不可行解可行化

输入：结点映射个体x;

输出：新的结点映射个体x′;

x′=x;

fori=1 toNvdo

Cap(1,i)=h(vi);

end

forj=1 toN′ do

c(j)是xj在个体x出现的次数，即映射到结点vxj上虚拟结点的个数；

diffCap(1,j)=h(vxj)-c(j);

end

forj=1 toN′ do

ifdiffCap(1,j)<0 do

η是diffCap中最大值所在的位置；

end

end

2.4 适应度函数

适应度函数是一个衡量个体好坏的标准，本文所建立的优化模型中的目标函数是最小化最大占用频隙号.因此本文采用的适应度函数为式(11)所示.

f=ρ+δ×ω,

(11)

其中δ是一个布尔型变量，当且仅当结点映射个体x和行路个体y组合形成一个解(x,y)是问题的可行解时δ=0，否则δ=1.ω是一个常数(该常数只要大于1即可，本文取ω=100).

3 实验与分析

3.1 参数设置

在仿真实验中，采用两种网络拓扑：网络拓扑1是包含13个节点和21个链路的NSFNET(如图1所示)， 网络拓扑2是包含20和节点和32个链路的ARPANET(如图2所示)， 链路上的数据表示网络节点间的距离.

图1 NFSNET拓扑Fig. 1 Topology of NFSNET

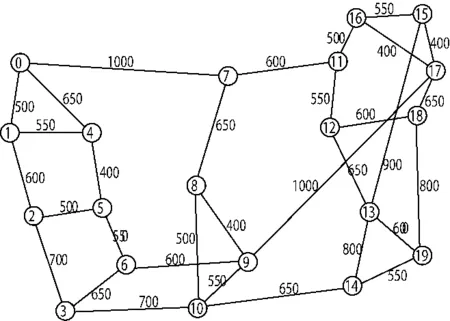
图2 ARPANET拓扑Fig. 2 Topology of ARPANET

仿真实验中假定每个频隙(Frequency Slots, FSs)为12.5 GHz，4种调制格式BPSK，QPSK，8QAM和16QAM的传输距离分别设置为9600、4800、2400和1200 km[10,11].物理网络中的每个物理结点上有10～20个虚拟机，当一个虚拟结点映射到物理结点上时需要占用该物理结点上的一个虚拟机.每一个虚拟网中有3～7个虚拟结点， 每两个虚拟结点之间有业务请求的概率是0.5.遗传算法中参数设置如下：种群规模Psize=100，交叉概率Pc=0.85，变异概率Pm=0.15，精英保留个数E=5，终止条件为进化代数Gmax=5000.

3.2 实验结果

为了验证算法的有效性，本文提出的算法(用GA表示)和文献[12]提出的算法(用LL表示)在不同的情况下进行对比.在本文设计的算法中，首先对业务按照某种策略排序，根据不同的排序策略可以产生不同的算法.本文采用三种常用的排序策略，即MSF(Most Subcarrier First, MSF)、LPF(Longest Path First, LPF)、EMkPSF(Extended Most K Path Subcarrier First, EMkPSF)，与本文提出的遗传算法结合可以得到三种算法，即GA-MSF、GA-LPF、GA-EMkPSF.图3和图4分别给出了α=0，β=1时在NSFNET和ARPANET中的实验结果；图5和图6分别给出了α=0.5，β=0.5时在NSFNET和ARPANET中的实验结果.图7和图8分别给出了α=1，β=0时在NSFNET和ARPANET中的实验结果.

图3 NSFNET中对比图(α=0，β=1)Fig. 3 Compared in NSFNET(α=0，β=1)

图4 ARPANET中对比图(α=0，β=1)Fig. 4 Compared in ARPANET(α=0，β=1)

3.3 实验结果分析

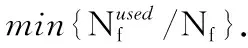
图5 NSFNET中对比图(α=0.5，β=0.5)Fig. 5 Compared in NSFNET(α=0.5，β=0.5)

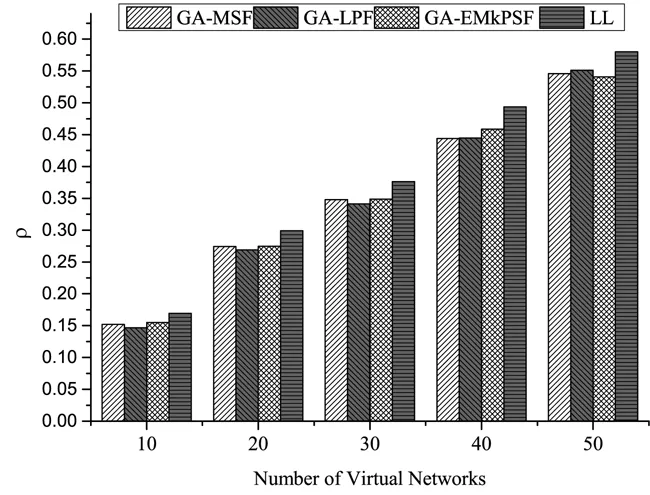
图6 ARPANET中对比图(α=0.5，β=0.5)Fig. 6 Compared in ARPANET(α=0.5，β=0.5)

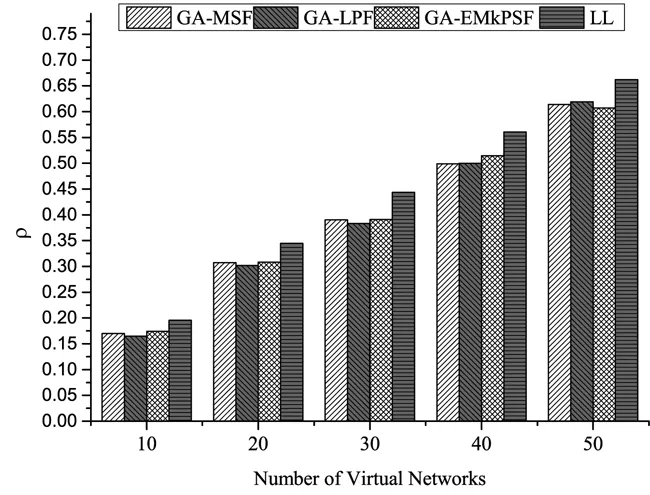
图7 NSFNET中对比图(α=1，β=0)Fig. 7 Compared in NSFNET(α=1，β=0)

图8 ARPANET中对比图(α=1，β=0)Fig. 8 Compared in ARPANET(α=1，β=0)

4 结论

本文针对虚拟弹性光网络中虚拟结点的映射及选路、频谱分配等问题进行了研究，建立了一个最小化占用频谱数及最小化最大占用频隙号为目标的全局约束优化模型.为有效地求解该约束优化模型，设计了全局优化算法.通过在不同的网络拓扑中进行仿真实验，实验结果表明：本文设计的算法可以有效降低网络中占用的频隙数和最大频隙号.但是算法的复杂度较大，因此在后续的研究中我们将降低计算复杂度，以快速地确定最优的虚拟节点映射及选路、频谱分配方案.