阻尼谐振子在非对易空间中的Wigner函数
2018-08-09王亚辉任亚杰
王亚辉,任亚杰
( 陕西理工大学 物理与电信工程学院,陕西 汉中 723001 )
0 引言
Wigner函数在描述量子计算、核物理、量子光学等方面有非常重要的作用[1],它是一个很好的半经典近似.1975年,Moyal从量子力学的内部逻辑出发,发现Wigner函数和已有的量子化方法(Schrodinger、Feymen路径积分量子化)是等价的,它的基本方程是Moyal星本征值方程.此刻Wigner函数才引起人们更大的关注,在这种逻辑完整而且独立的量子化方法中,不需要选定一个特定的表象空间.在这种MOYAl量子化方法提出不久,超弦理论的工作者提出了弦尺度下的非对易几何的概念[2].超弦/M理论中出现的非交换几何,使得人们不仅能运用非交换几何的概念和定理来有效地分析对偶性、BPS态以及D-膜动力学等,而且引起了人们对整个物理学理论基础的理解及更深刻的认识变革.文献[3-6]对谐振子的量子力学问题进行了研究,文献[7-9]研究了非对易空间的量子力学模型,文献[10-14]研究了非对易空间物理模型的Wigner 函数,人们对Wigner 函数在非对易空间的应用引起了极大的关注.这种非对易量子效应可以与Moyal的量子化方法表述为相同的形式.
在经典力学中,一个粒子的运动状态,用它在每一时刻的坐标和动量,即相空间中的一个点来描述,在量子力学中,由于波动-粒子两象性,一个体系的量子态,如选用一个连续表象,则量子态表示成一个波函数(复),其包含了体系的全部信息[15].用量子力学的思维来处理经典物理模型.本文利用Wigner函数的基本性质和空间变量的对易关系中包含的坐标-坐标的非对易性, 用量子力学来处理阻尼系统,得到了阻尼谐振子在非对易空间中的Wigner函数.
1 量子系统的Wigner函数
1.1 对易空间中Wigner函数
在对易空间中,定态 Schrodinger方程常被写成Hψn(x)=Enψn(x),那么Wigner函数的标准形式就可写为[4]
(1)
由文献[5]可知:
H*Wn=Wn*H=EnWn.
(2)
在二维情况下, *被定义为[5]
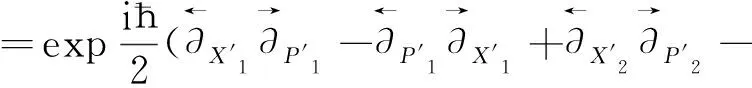
(3)
1.2 非对易空间中Wigner函数
由文献[5]可知,在非对易空间中,当*在二维情况下被重新定义为:
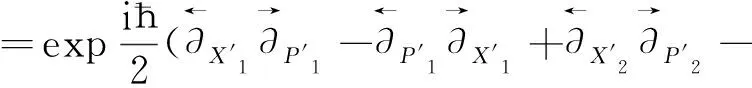
(4)
时,式(2)依然成立,变为
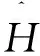
(5)
2 二维阻尼谐振子的Wigner函数
2.1 阻尼谐振子的量子力学处理
设二维阻尼谐振子的运动方程为:
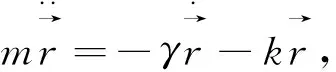
(6)
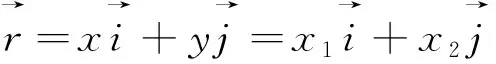
取广义坐标X1=x1eγt/2m,X2=x2eγt/2m,由文献[3,6]可得广义动量为:
(7)
可以证明广义坐标和广义动量的对易关系为:
[X1,P1]=iħ,[X2,P2]=iħ,
故系统的Hamiltonian算符为:
P1X1+X2P2+P2X2)+
(8)
令
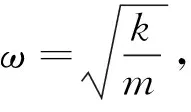
式(8)化简为
(9)
将式(9)代入方程H*Wn=Wn*H=EnWn可得:
H*W=W*H=EW.
(10)
2.2 对易空间中二维阻尼谐振子的Wigner函数
将式(3)、(9)代入式(10)得:
(11)
(12)
由式(11)等于式(12)得:
(13)
(14)
再令:
(15)
将式(15)代入式(13)得:
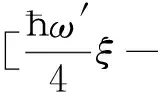
E1]W1(ξ)=0.
(16)
化简式(16)得:
(17)
定义
(18)
式(17)化简为
(19)
其中L(ξ)表示拉盖尔多项式 ,
(20)
所得Wigner函数为:
W1(ξ)=W1(X′1,P′1)=
(21)
同理计算式(14)可得:
(22)

Wn,m=W1(ξ)W2(η)=
(23)
2.3 非对易空间中二维阻尼谐振子的Wigner函数
(24)
其中:
(25)
(26)
*被重新定义,将式(4)和式(25)代入式(5),考虑到θ是个小量,忽略θ2及更高次项可得:
(27)
(28)
由式(27)等于式(28)得:
E1}W1=0.
(29)
令:
(30)
其中
将式(30)代入式(29)得:

E1]W1(ξ′)=0.
(31)
利用与式(17)-(21)相似过程得Wigner函数为:
(32)
同理计算式 (26)可得:
(33)
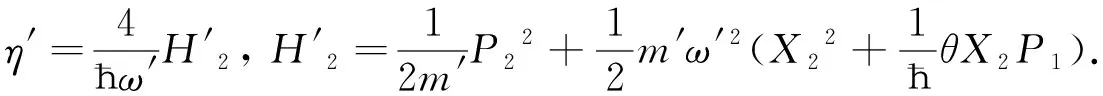
所以对易空间中二维阻尼谐振子的Wigner函数为:
W1(ξ′)W2(η′)=
(34)
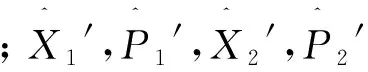
3 结论
Wigner函数是相空间中的准分布函数,是一个实函数且满足边缘条件,在现代量子测量中具有重要的意义.文章简单介绍和讨论了哈密顿函数在对易空间和非对易空间Wigner函数的性质,得到的非对易空间中阻尼谐振子的Wigner函数形式与对易空间一致.并且与利用原始定义积分得到的结果完全一致.阻尼谐振子是许多复杂模型的基础,可用来讨论许多的实际问题,为进一步研究物理模型在非对易空间和非对易相空间的Wigner函数奠定了基础.更重要的是提供了一种用量子力学方法来处理经典物理问题的方式.
