绝对值方程的非单调光滑算法
2018-08-09董丽
董 丽
(信阳师范学院 数学与统计学院, 河南 信阳 464000)
0 引言
考虑绝对值方程(AVE):
Ax+B|x|=b,
(1)
其中:A∈Rn×n,B∈Rn×n,B≠0,b∈Rn,|x|表示对x的各个分量取绝对值.绝对值方程(1)由Rohn提出[1].许多优化问题,比如线性互补问题、线性规划问题、凸二次规划问题等,都可以转化成绝对值方程(1)进行求解[2].因此,绝对值方程(1)具有重要的研究意义.
目前,求解绝对值方程的算法主要针对如下形式的绝对值方程:
Ax-|x|=b.
(2)
文献[3]给出了一个求解AVE(2)的Levenberg-Marquard方法,讨论了算法的收敛性质.文献[4]给出了求解AVE(2)的一个松弛非线性PHSS型迭代方法,证明了算法的收敛性.文献[5]给出了求解AVE(2)的一个混合算法,在适当条件下证明了算法有限步终止.光滑牛顿法是近年来求解优化问题的一类新方法[6,7].最近,文献[8]提出了一个求解AVE(1)的光滑牛顿法,在假设条件矩阵A最小的奇异值严格大于矩阵B最大的奇异值下,证明了算法具有全局和局部二次收敛性质.
本文给出了一个求解AVE(1)的非单调光滑算法,在文献[8]假设条件下证明了算法具有全局和局部二次收敛性质.与文献[8]中的光滑算法相比,本文算法采用一种新的非单调线性搜索技术,其包含文献[8]所采用的单调线性搜索以及文献[9,10]所研究的非单调线性搜索.
1 算法设计
对任意的(μ,x)∈R1+n,定义H:R1+n→R1+n如下:
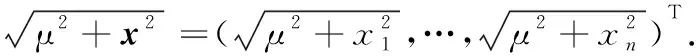
(i)H(μ,x)=0当且仅当x为(1)的解.
(ii)H(μ,x)在R1+n{(0,0)}上连续可微,其雅克比矩阵为
这里
(iii)H在R1+n上强半光滑.
为建立算法,本文采用文献[8]中的假设条件.
假设1 矩阵A最小的奇异值严格大于矩阵B最大的奇异值.
在假设1下,下面结论成立,其证明见文献[8]中的推论2.3.
引理1 如果假设1成立,则对任意的b∈Rn,绝对值方程(1)唯一可解.
为简单,记z=(μ,x)∈R1+n,并定义价值函数f(z)=‖H(z)‖2.下面给出算法.
算法(A)(一个非单调光滑算法)
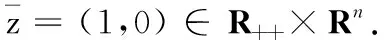
(C1) 对任意的k≥0有ξk≥1;
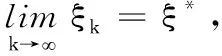
令k=0.
步骤1 若‖H(zk)‖=0,则停止迭代.否则,计算
(3)
步骤2 通过求解方程组
(4)
得搜索方向Δzk=(Δμk,Δxk)∈R×Rn.
步骤3 令αk为1,λ,λ2,…中使得下式成立的最大值
f(zk+αkΔzk)≤[1-2σ(1-γ)αk]Λk.
(5)
步骤4 令zk+1=zk+αkΔzk.令
(6)
令k=k+1.转步骤1.
注在步骤0中,需要选取数列{ξk}⊂R++满足条件(C1)和(C2).事实上,有很多数列满足上述要求,比如
(i)ξk=ξ,其中ξ≥1为常数;
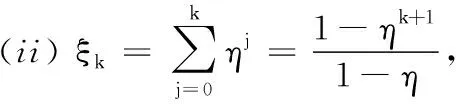
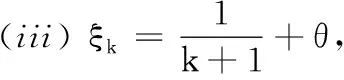
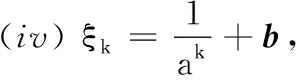
•如果选取ξk=1,则对任意的k≥0有Λk=f(zk).在这种情况下,步骤3即为传统的单调线性搜索[8].
•如果选取ξk=ξ,其中ξ≥1为常数,则步骤3即为文献[9]所讨论的非单调线性搜索.
•文献[10]提出了一种非单调线搜索准则,其定义如下:令ξ0=1,选取ηmin和ηmax使得0≤ηmin<ηmax<1,并选取ηk∈[ηmin,ηmax].然后,令
ξk+1=ηkξk+1,
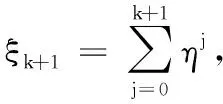
为证明算法(A)有好的定义,需要如下两个引理,其中引理2的证明见文献[8]中的定理3.2.
引理2 如果假设1成立,则对任意的μ>0有H′(z)可逆.
引理3 假设{Λk}和{zk}由算法(A)产生,则下列结论成立:
(i){Λk}单调下降有下界,因此收敛.

(iii)对任意的k≥0有f(zk)≤Λk.
证明由步骤3和步骤4可知
(7)
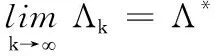
(8)
在不等式(8)两边同时取极限可得
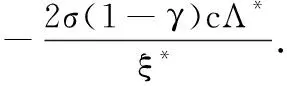
进而再由Λ*>0可知
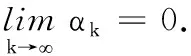
f(zk+1)=ξk+1Λk+1-(ξk+1-1)Λk≤
ξk+1Λk+1-(ξk+1-1)Λk+1=Λk+1,
其中不等式利用了结论(i)以及ξk≥1.注意到Λ0=f(z0).因此,结论(iii)成立.证毕.
定理1 如果假设1成立,则算法(A)有好的定义,并产生无穷点列{zk=(μk,xk)}.此外,对任意的k≥0都有μk>0.
证明假设对于某个k有μk>0,比如k=0.由引理2可知矩阵H′(zk)非奇异,故步骤2在第k次迭代有好的定义.对任意的α∈(0,1],定义
Fk(α)=f(zk+αΔzk)-f(zk)-αf′(zk)Δzk.
(9)
因为f在任意的z∈R++×Rn处连续可微,故由式(9)可知Fk(α)=o(α).由ωk的定义可知
ωk≤γmin{1,f(zk)}=
γmin{1,‖H(zk)‖2}≤γ‖H(zk)‖.
(10)
因此,由式(4),(9)和(10)可知,对任意的α∈(0,1]有
f(zk+αΔzk)=f(zk)+αf′(zk)Δzk+Fk(α)=
f(zk)+2αHT(zk)H′(zk)Δzk+o(α)=
(1-2α)f(zk)+2α‖H(zk)‖ωk+o(α)≤
(1-2α)f(zk)+2αγf(zk)+o(α)≤
[1-2(1-γ)α]f(zk)+o(α).
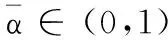
f(zk+αΔzk)≤[1-2σ(1-γ)α]f(zk)≤
[1-2σ(1-γ)α]Λk.
这里第2个不等式利用了引理3(iii).因此,步骤3在第k次迭代时有好的定义,并产生步长αk∈(0,1].由式(4)可知Δμk=-μk+ωk,故
μk+1=μk+αkΔμk=(1-αk)μk+αkωk>0.
(11)
因此,由μ0>0以及上面的证明过程可知算法(A)有好的定义,并产生无穷点列{zk=(μk,xk)}.此外,对任意的k≥0都有μk>0.证毕.
2 算法收敛性分析
本节分析算法(A)的收敛性质.为此,需要如下引理.
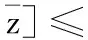
引理4 设{zk=(μk,xk)}为算法(A)产生的迭代点列,则对任意的k≥0有μk≥ωk和μk≥μk+1.
证明由步骤0和式(3)可知μ0≥γ≥ω0,并且{ωk}单调下降.假设对于某个k有μk≥ωk.由式(11)可知
μk+1≥(1-αk)ωk+αkωk=ωk≥ωk+1,
故由数学归纳法可知对任意的k≥0有μk≥ωk.进一步,由式(11)可知,对任意的k≥0,有μk+1≤(1-αk)μk+αkμk=μk.证毕.
定理2 如果假设1成立,则算法(A)产生的迭代点列{zk=(μk,xk)}有如下两个性质:
(i){zk}有界;
(ii){zk}的任意聚点z*=(μ*,x*)都满足方程H(z)=0.
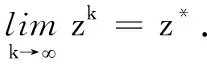
下面假设ω*>0.因为{ωk}单调下降,故由引理4可知
μk≥ωk≥ω*>0.
(12)
此外,由引理3可得
(13)
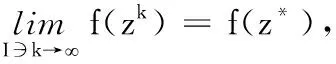
由式(12)和式(13)可知
Λ*≥f(z*)≥(μ*)2≥(ω*)2>0.
因此
(14)
因为μ*≥ω*>0,故f(z)在z*处连续可微.此外,由引理2可知H′(zk)可逆,故由式(4)可知{Δzk}k∈I收敛,记

利用式(10),在不等式(14)两边同时取极限可得
-2σ(1-γ)f(z*)≤2HT(z*)H′(z*)Δz*=
2[-f(z*)+‖H(z*)‖ω*]≤
2[-f(z*)+‖H(z*)‖ω*]≤
-2(1-γ)f(z*).
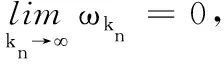
由式(6)可知
令kn→,则有
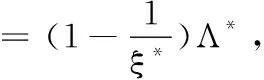
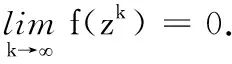
设z*为{zk}的任意聚点,则由文献[8]中的引理4.3可知,所有的V∈∂H(z*)都是非奇异的.利用这个结论,类似于文献[11]中定理5.3的证明过程,我们可以得到算法(A)的局部收敛性质.
定理3 设{zk}为算法(A)产生的迭代点列,并且z*为{zk}的任意聚点,则{zk}收敛到z*.此外,当k充分大时有‖zk+1-z*‖=O(‖zk-z*‖2).
3 数值试验
为检验算法(A)的实际计算效果,本节用MATLAB R2012b编程,在Intel(R) Core(TM) i7-790 CPU 3.60 GHz, 8.00 GB内存, Windows XP操作系统的电脑上做数值试验.利用算法(A)去求解AVE(2).在测试过程中,初始点选为x0=rand(n,1),参数选为μ0=10-2,σ=0.2,λ=0.8,γ=10-3,ξk=1/2k+10,终止准则为‖Axk-|x|-b‖≤10-8.
问题1 选取A∈Rn×n,其对角线上的元素为500,而非对角线上的元素在区间[1,2]上任意选取.然后令b=(A-I)e,这里I为单位矩阵,e=(1,…,1)T.易知,问题1有精确解x=(1,…,1)T.首先我们利用算法(A)求解1次问题1,图1显示了算法(A)的收敛性,其中横轴为迭代次数k,纵轴为lg(‖Axk-|xk|-b‖).然后,利用算法(A)求解10次问题1.数值结果列于表1,其中MIT表示求解10次问题1所需迭代次数的最小值,AIT表示求解10次问题1所需迭代次数的平均值,ACPU表示求解10次问题1所需的CUP时间(单位:s),AV表示求解10次问题1的‖Axk-|xk|-b‖的平均值.
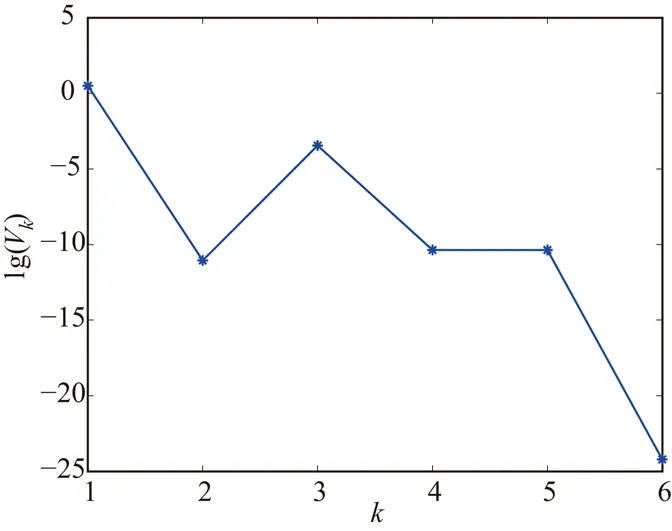
图1 算法(A)求解1次问题1(n=1000)时的收敛性Fig. 1 Convergence of algorithm (A) for solving one problem 1 (n=1000)

nMITAITACPU/sAV 100066.00.384.1827E-011200066.02.451.5341E-010300066.06.843.6166E-010400066.014.486.0066E-010500066.026.158.3216E-010
问题2 选取A∈Rn×n,其中
aii=4n,ai,i+1=ai+1,i=n,aij=0.5,i=1,2,…,n.
然后令b=(A-I)e.易知,问题2有精确解x=(1,…,1)T.同样利用算法(A)求解10次问题2.数值结果列于表2.

表2 算法(A)求解问题2的结果Tab. 2 Numerical results of algorithm (A) for problem 2
