分析初中数学中两种常见的知识类型

吴应浩

（成都石室中学初中学校青龙校区，四州 成都）

在当前教学工作的开展中，更加注重数学实际问题与生活、生产以及经营问题进行有效的结合，更加重视学生多种能力的提升。为了切实践行素质教育工作内涵，文本将针对初中数学中两种常见的知识类型进行详细分析。

一、方案设计知识类型

针对方案设计型的知识问题，便是给予学生一个实际的情境，并给出学生若干问题，引导学生针对具体的问题给出一个最佳解决问题。方案解决类知识主要考查的是学生的问题处理能力以及问题解决的能力。需要教师积极结合数学知识，提升学生的阅读理解能力和信息处理能力、文字概括能力等多种能力，以便于切实增强学生解决问题的能力。

1.设计测量方案问题

针对设计测量的方案问题，所考察的知识层面也相对较为广泛，主要的内容会涉及不能直接测量的小山高度、水塘的宽度以及园的直径等多种问题，并且题型会涉及多种开放题型。例如，如图1，某高为为12.6米的教学楼ED前有一棵大树AB，在某一时刻测量得大树AB、教学楼ED在太阳的投影下的投影长度分别是BC=2.4米，DF=7.2米，求大树AB的高度。

此类知识便是针对实际测量方案类问题进行考查，主要考查的内容主要是三角形相似的证明问题，考查了学生的划归思想以及关联思想的运用，是典型的运用几何思想开展设计测量方案的主要案例。

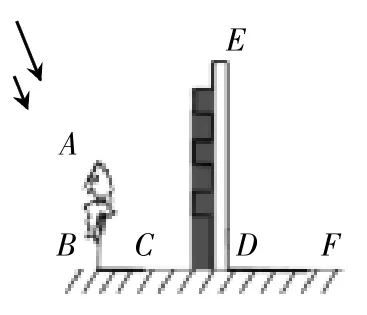
图1

2.最佳设计方案问题

最佳设计方案的相关问题，往往会涉及选出最短路线、运费最少等多种形式。针对最佳设计方案的问题，看似是一种相对开放的问题，实际是与初中知识教学的不等式、函数以及几何内容密不可分的教学内容。

例如，老师为了引导学生积极地参与文体活动，所以准备在本班的班费中拿出200元购买运动设备。已知羽毛球与棒球的单价比例为2∶3，单价之和是80，求羽毛球与棒球的单价分别是多少？若要买羽毛球与棒球的总数一共是36个，并且羽毛球的数量多于25个，会有几种购买方案？

切实地将生活实际与数学知识进行紧密的联系，让学生切实结合自身的阅历以及生活经验去感知与考虑问题，学会引导学生利用数学知识构建出题目中的不等量关系。在头脑中构建出思维模式，并通过解模针对实际的数学问题进行求解作答。切实利用最佳设计方案，增强学生的数学理解能力以及数学运用能力。

二、动态几何知识类型

动态几何知识类型主要是突出了几何问题的动态化，其主要考查的思想便是数形结合的思想以及几何动态的思想，实际地考查了学生的函数知识以及几何知识的内容。针对动态问题，主要是通过数学图形，表达某一图形的动态变化，揭示了在动态图形中动态与静止之间的关系。所以在针对动态几何问题解题时，应该更加注重几何元素运用的方向以及途径，针对具体问题进行具体的分析。

1.建立函数方程或不等式模型求解方法

针对建立函数方程或不等式模型求解方法来说，主要是结合数学知识的实际特点，将变量和不变量有机转化，构建成特殊而关系以及特殊值的形式，通过函数方程模型进行解答。

例如，如图 2，在梯形 ABCD 中，AD∥BC，AD=2，BC=4，点 M是AD的中点。

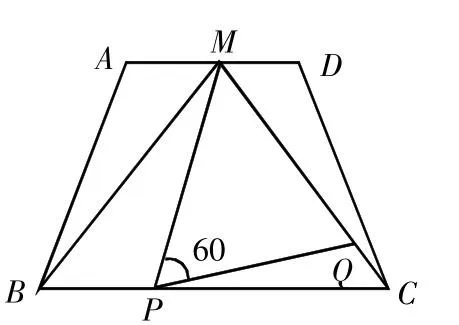
图2

（1）求证梯形ABCD是等腰梯形。

（2）动点P、Q分别是在线段BC和MC上运动，∠MPQ=60°保持不变，设PC=x，MQ=y，求y与x之间的函数关系。

（3）在（2）中，当 y取最小值时，判断△PQC的形状，并说出理由。

针对此类动态几何问题，来说，其中（2）与（3）明确涉及函数方程与不等式模型求解的内涵，尤其是针对（3）来说，问题条件回归到了动点静止的问题中，通过第二问的函数可以求出当x对称轴的值y有最小值，便可以通过给定的条件PC=2来求△PQC的形状问题。

2.数形结合与转换的数学思想

针对数形结合与转换的数学思想来说，主要应该找出几何图像中数形结合的内容，并通过已经给出的数学条件构建出一个动态化的数学途径，并利用动态转化的形式，进行问题解决。

例如，如图3，抛物线y=x2与直线相交于点O、A两点，点P沿着抛物线从点A出发，按横坐标大于点A的横坐标方向运动，PS∥x轴，交直线OA于点 S，PQ⊥x轴，垂足为 Q，R，当 P的横坐标为2时。

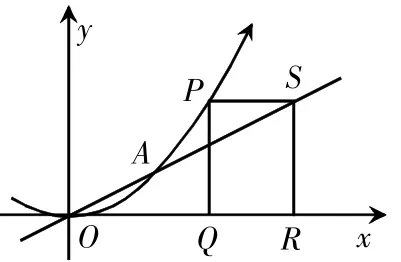
图3

（1）求S点的坐标，通过原点，且平分矩形PQRS的直线解析式。

（2）当矩形PQRS为正方形时，求点P的坐标。

此题便是切实要求学生利用数形结合的形式，在坐标中，动态化的针对矩形PQRS进行探究，需要学生针对坐标构建出一个动态化的思维建模，并针对实际情况以及图形的特点，针对图形内容进行解答。

总而言之，初中数学常见的两种知识类型便是动态几何问题以及方案设计问题。通过这两种类型的知识内容，切实拓展了学生的动态化思维、锻炼了学生的逻辑思维能力，有利于增强学生的数学思维水平。教师应该详细针对初中初学知识的两种类型进行详细的分析，切实促进学生的全面发展，促进数学教学的工作开展。