运用平方差公式进行计算过程中存在的问题及应对策略
2018-08-08金培苗
金培苗
(灌云县九年制实验学校,江苏 灌云)
平方差公式是苏科版七年级数学下册第9章第4节第二课时所学习的内容,学生对于平方差公式都能说上来:(a+b)(a-b)=a2-b2,但是在运用过程中,总会出现各式各样的错误。下面我就针对存在的问题和大家谈谈应对策略。
一、练习中的错误举例
错误类型 1:(x+3)(x-3)=(x-3)2(x-3)(x-3)=x2-32
错误原因剖析:平方差公式的结构特点没有掌握,与完全平方公式的特点弄混了。
错误类型 2:(-2+x)(2+x)=(-2)2-x2=4-x2(-3+x)(x+3)=(-3)2-x2
错误原因剖析:没有掌握好平方差公式的特点,后面的结果前后两部分弄颠倒了。
错误类型 3:(2x-3y)(2x+3y)=2x2-3y2
错误原因剖析:没有掌握好平方差公式的特点,套用公式时丢掉了括号。
错误类型 4:(2a-3b+c)(2a+3b+c)=(2a-3b)2-c2=4a2-12ab+9b2-c2
错误原因剖析:没有掌握好平方差公式的特点,没有弄清哪些是相等的量、哪些是互为相反数的量。
二、应对策略
1.弄清公式特点和条件
平方差公式左边前后括号里的多项式的项数相同,其中在前后括号里有一部分项是相等的,另外一部分则是互为相反数的。公式右边有两部分,前部分是相等量的平方,后部分是互为相反数的量的项的平方,中间用“—”号连接。如下图:
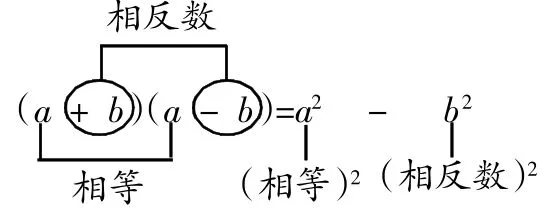
使用平方差公式进行计算必须满足如下几个条件:
(1)前后括号内的项数要相同;
(2)前后括号内要有相等的项,前面括号内余下的项和后面括号余下的项是互为相反数关系。
2.教会学生套用公式
在解题的时候一定要认真审题,找到前后括号内相等的项和互为相反数的项,然后根据上面的公式进行计算。
例 1 计算:(1)(2a-3b)(2a+3b) (2)(3x-y)(-y-3x)
解析:在(1)中第一个括号内2a和第二个括号内的2a是相等的项,第一个括号内-3b和第二个括号内3b是互为相反数的项,所以根据公式可得:(2a)2-(3b)2,然后再依据积的乘方公式进行计算即可。在(2)中第一个括号内-y和第二个括号内的-y是相等的项,第一个括号内3x和第二个括号内-3x是互为相反数的项,所以根据公式可得:(-y)2-(3x)2,然后再依据积的乘方公式进行计算即可。
解题过程如下:

对于复杂的题目也是一样的操作方式,例如:
例 2 计算:(1)(2a+3b+c)(2a+3b-c)
(2)(3x-y-4z)(4z-y+3x)
解析:在(1)中第一个括号内2a,+3b和第二个括号内的2a,+3b是相等的项,第一个括号内+c和第二个括号内-c是互为相反数的项,所以根据公式可得:(2a+3b)2-(c)2,然后再依据相关公式进行计算即可。在(2)中第一个括号内3x,-y和第二个括号内的3x,-y是相等的项,第一个括号内-4z和第一个括号内4z是互为相反数的项,所以根据公式可得:(3x-y)2-(4z)2,然后再依据相关公式进行计算即可。
解题过程如下:
(1)(2a+3b+c)(2a+3b-c)
解:原式=(2a+3b)2-(c)2
=(2a)2+2·2a·3b+(3b)2-c2
=4a2+12ab+9b2-c2
(2)(3x-y-4z)(4z-y+3x)
解:原式=(3x-y)2-(4z)2
=(3x)2-2·3x·y+(y)2-16z2
=9x2-6xy+y2-16z2
注意:在套用公式的过程中要注意,我们找到相等的项,将它们连同它们的符号直接填入前面的括号里然后把它们的和加平方;至于互为相反数的项,我们只选择前一个括号余下的项,要连同本身的符号直接填入后面的括号里,然后加平方(也可以选择后面括号里除去与前面括号里相等的项余下的项,也要连同其符号一起填入后面的括号里,然后加平方)。
例 3 计算(2a-3b+5c-4d)(4d-3b-5c+2a)
解析:此题前后括号内的项数都是4,而且前后括号内有相等的项,然后前后括号内剩下的项是互为相反数,可以套用平方差公式计算。在第一个括号内2a,-3b和第二个括号内的2a,-3b是相等的项,第一个括号内+5c,-4d和第二个括号内-5c,4d是互为相反数的项,所以根据公式可得:(2a-3b)2-(5c-4d)2,然后再依据相关公式进行计算即可。解题过程如下:
解:(2a-3b+5c-4d)(4d-3b-5c+2a)
=(2a-3b)2-(5c-4d)2
=(4a2-12ab+9b2)-(25c2-40cd+16d2)
=4a2-12ab+9b2-25c2+40cd-16d2
从上述几个例子可以看出,运用平方差公式进行计算,可以使计算过程变得简便。但要强调的是,用平方差公式进行计算,前提是所给的题目的特点要符合平方差公式的特点和条件,如果不符合,则不可乱用,否则会弄巧成拙。因此,只有弄清公式的结构特点,然后再套用上面所给定的公式完成计算,才能达到简便、准确、高效、快捷的效果。
