考虑通行能力折减的可变车道优化

蔡建荣，黄汝晴，黄中祥



考虑通行能力折减的可变车道优化

蔡建荣1，黄汝晴2，黄中祥1

(1. 长沙理工大学 交通运输工程学院，湖南 长沙，410114；2. 中南大学 交通运输工程学院，湖南 长沙，410075)

为有效缓解因潮汐现象所导致的交通拥堵和道路资源闲置并存的问题，在考虑车道数对路段单向通行能力影响的基础上研究可变车道优化设置方法。该方法在确保可变车道实施过程中轻交通流方向正常通行的前提下，基于非均衡经济学理论的价格−数量调节，以系统总出行时间最小为目标构建可变车道优化的混合整数双层规划模型，并采用粒子群优化算法对模型进行求解，以算例的形式验证模型和算法的有效性。研究结果表明：从系统层面优化可变车道设置能够充分利用轻交通流方向闲置的道路资源来提高重交通流方向路段的容量，从而改变其行程时间函数，进而调节流量在路网上的分布并均衡各路段的饱和度；使道路网络结构更好地匹配出行需求，在道路资源一定的情况下有效地降低系统总出行时间。

交通工程；潮汐现象；可变车道；双层规划；粒子群优化算法

随着经济社会的迅猛发展，城市中心区居住用地趋于饱和，越来越多的城市居民选择在中心区上班，在郊区生活[1]。职住不平衡导致城市交通的潮汐特性十分明显，在高峰期间，道路某一方向的流量大于容量，而另一方向的车道未得到充分利用[2]，这实质上是居民出行市场中供求失衡的时空表现形式之一，也是价格(旅行时间)不能完全调节供求关系实现瓦尔拉斯均衡的体现[3]。根据国内外实践经验，调整道路时空资源，实施可变车道是解决潮汐交通现象的有效措施[4−6]，也是非均衡经济学理论中数量调节在交通管理方面的典型应用。通过将轻交通流方向的道路资源调节给重交通流方向，不仅能减缓重交通流方向的交通压力，而且可避免不必要的道路建设，节省资源，并有助于提高整个交通系统的运行效率[7]。WOLSHON等[8]对可变车道设置能够解决的问题进行了分析，指出在规划可变车道时应着重对各种设计方案的费用、优缺点以及整个交通系统的长远效益进行综合考虑。WALECZEK等[9]研究了可变车道系统对交通流和道路安全的影响，认为可变车道系统是一种实用、安全的智能交通管理工具。LAURENCE等[10]通过对不同地点不同情况下设置的可变车道交通特性进行分析，论证了可变车道的通行能力与正常车道的通行能力相近，而不是通常所认为的只有正常车道通行能力的一半。DEY等[11]从基础设施利用率、安全、经济发展的角度对华盛顿州的可变车道设置方案进行了评估。BEDE等[12]指出可变车道能够在现有道路基础上很好地应对主要拥挤方向的交通量动态变化，车流密度是可变车道调节的重要参考依据，并基于一个被分割成多个单元的路网构建了可变车道系统模型。陈坚等[13]通过对成都市蜀西路交通特性进行分析，提出了适用于潮汐车流路段的可变车道具体设置方案。张卫华 等[14]采用熵值法对城市道路通行效率进行了评估，并结合通行能力模型提出了可变车道实施效果评价模型及相关计算方法。韩璧磷等[15]以最小延误费用为目标构建了可变车道数调整模型，并指出当方向分布系数大于等于2/3时，可变车道的设置能有效降低系统总延误费用。张鹏等[16]采用可变车道和信号配时联合优化方法，通过合理调节路段阻抗及交通分布，从而使路网容量达到最大。史峰等[17]探讨了可变车道设置方案的优化要点，分析了交通组织者和出行者之间的主从博弈关系。高自友等[18−19]以路网总阻抗最小为目标构建了可变车道优化双层规划模型，但该模型将双向路段更改为单向路段的决策，忽略了新交通组织设计的成本，破坏了整个系统的连通性和有效性。上述关于可变车道的研究均假定路段通行能力与车道数成绝对正比关系，但事实上，随着车道数的增加，平均每车道通行能力的增加是边际递减的，在可变车道优化中，车道数对通行能力的影响不能忽视[20]。为此，本文作者以维持可变车道实施过程中轻交通流方向的正常通行为基本前提[21]，考虑车道数对路段通行能力的折减影响，基于非均衡经济学理论的价格−数量调节[22]，从系统优化的角度采用双层规划方法对可变车道优化设置方案进行研究，以期在确保整个交通系统有效性的同时，缓解交通拥堵和道路资源闲置并存的问题。

1 车道数对路段通行能力折减分析

路段单向通行能力随车道数的增加而增加，但随着车道数增加，车辆换道机会也相应增大，车辆之间的相互干扰增大，路段实际通行能力的增加随着车道数的增加而边际递减[23]。根据杨小宝等[24]的研究成果，设2条车道路段的平均车道通行能力为2，换道频率为2(2=−0.224)，则条车道路段的平均车道通行能力c为

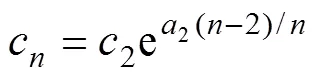
由此可以得到不同车道数(≥2)的平均车道通行能力，如表1所示。

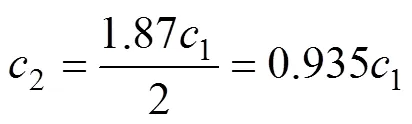
取单位冲激序列为

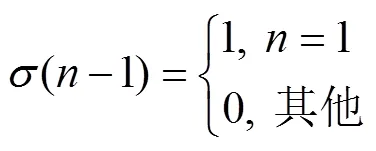
单位阶跃序列为

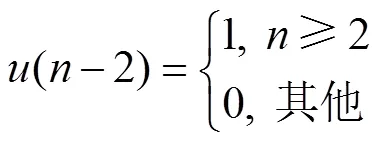
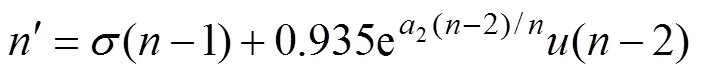
表1 平均车道通行能力

表2 平均车道利用系数

2 可变车道优化双层规划模型

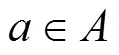
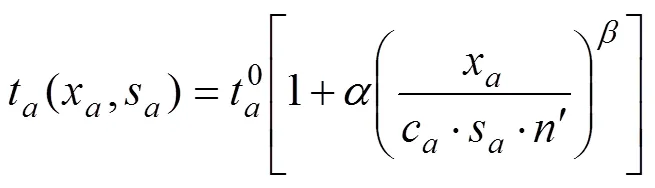
假设所有出行用户具有选择最小出行费用路径的倾向，通过价格调节作用，最终出行用户的路径选择行为符合Wardrop第一原理，路网达到用户均衡状态。交通管理部门针对可变车道系统，通过数量调节作用能够优化道路资源的分配，使道路网络结构更好地匹配城市居民出行需求。基于非均衡经济学理论的价 格−数量调节，以整个路网的总出行时间最小为目标，构建可变车道优化的混合整数双层规划模型如下。

上层规划：

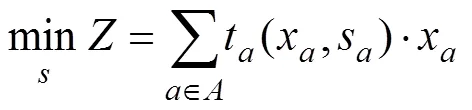
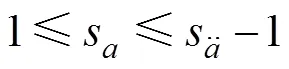
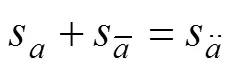
下层规划：

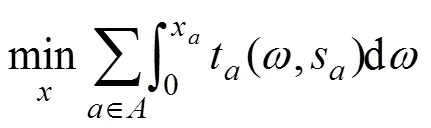
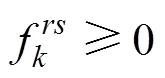
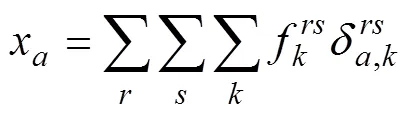
3 模型求解算法

模型(6)~(12)是一个非线性混合整数双层规划问题，求解困难，智能优化算法是解决该类问题的较好方法。粒子群优化算法是一种并行算法，从随机解出发，通过迭代来寻找最优解，具有实现容易、精度高、收敛快等优点[26−27]。本文采用该算法来求解可变车道优化模型，算法步骤如下。

Step 2：计算适应度。针对每个可行粒子求解下层用户均衡交通分配模型，再根据路段流量求解上层目标函数值，即为该粒子的适应度。

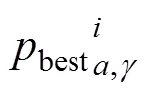
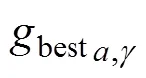
4 算例分析

图1 测试路网

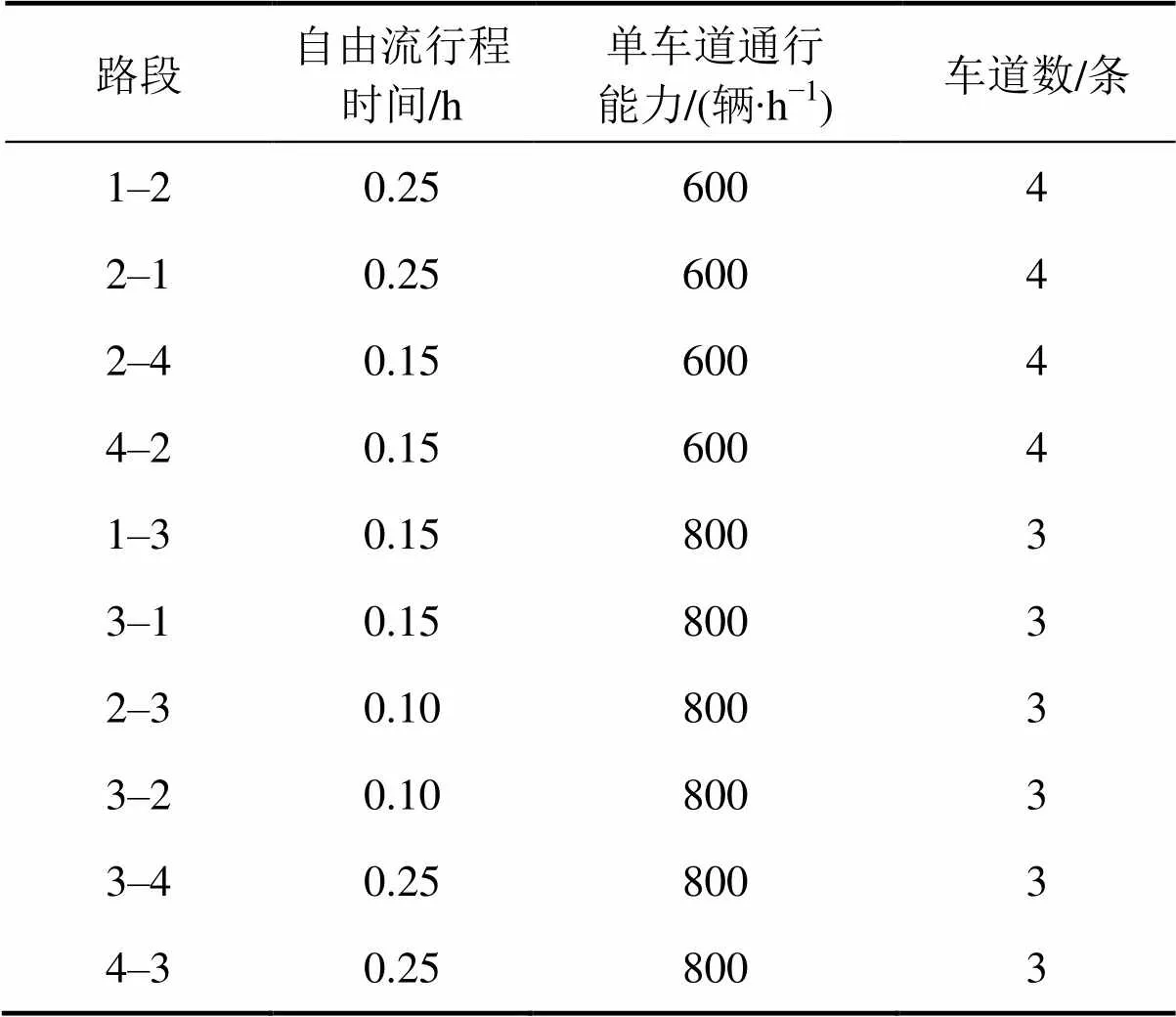
表3 路段特性参数

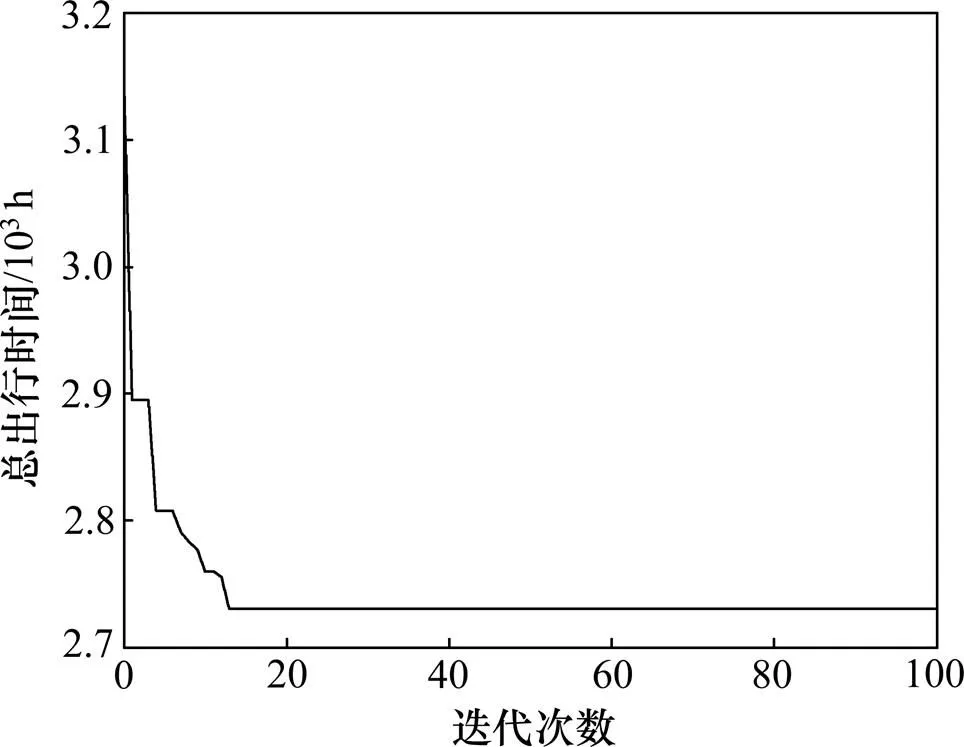
图2 系统总出行时间随迭代次数的变化

可变车道优化设置前后各路段的车道数、容量、流量、饱和度以及行程时间等特征值对比如表4所示。

从表4可以发现：可变车道优化设置之前，路段1–2，2–4，1–3及3–4的饱和度均超过1，表明路段十分拥堵；路段2–1，4–2，3–1及4–3的饱和度均小于等于0.3，表明路段流量较少，道路资源没有得到充分利用。双向路段潮汐现象明显，交通拥堵和道路资源闲置并存的问题突出。可变车道优化设置之后，轻交通流方向路段的车道数有所减少，路段容量相应减少，而重交通流方向路段的车道数有所增加，路段容量也相应增加，行程时间则相应减少。各路段的饱和度均介于0.55~0.85之间，路段既不过度拥堵，也没有道路资源闲置造成资源浪费。这说明可变车道优化方案能充分利用轻交通流方向闲置的道路资源来提高重交通流方向路段的容量，进而调节流量在路网上的分布，降低重交通流方向路段的行程时间并均衡各路段的饱和度，有效缓解因潮汐现象所导致的交通拥堵和道路资源闲置并存的问题。

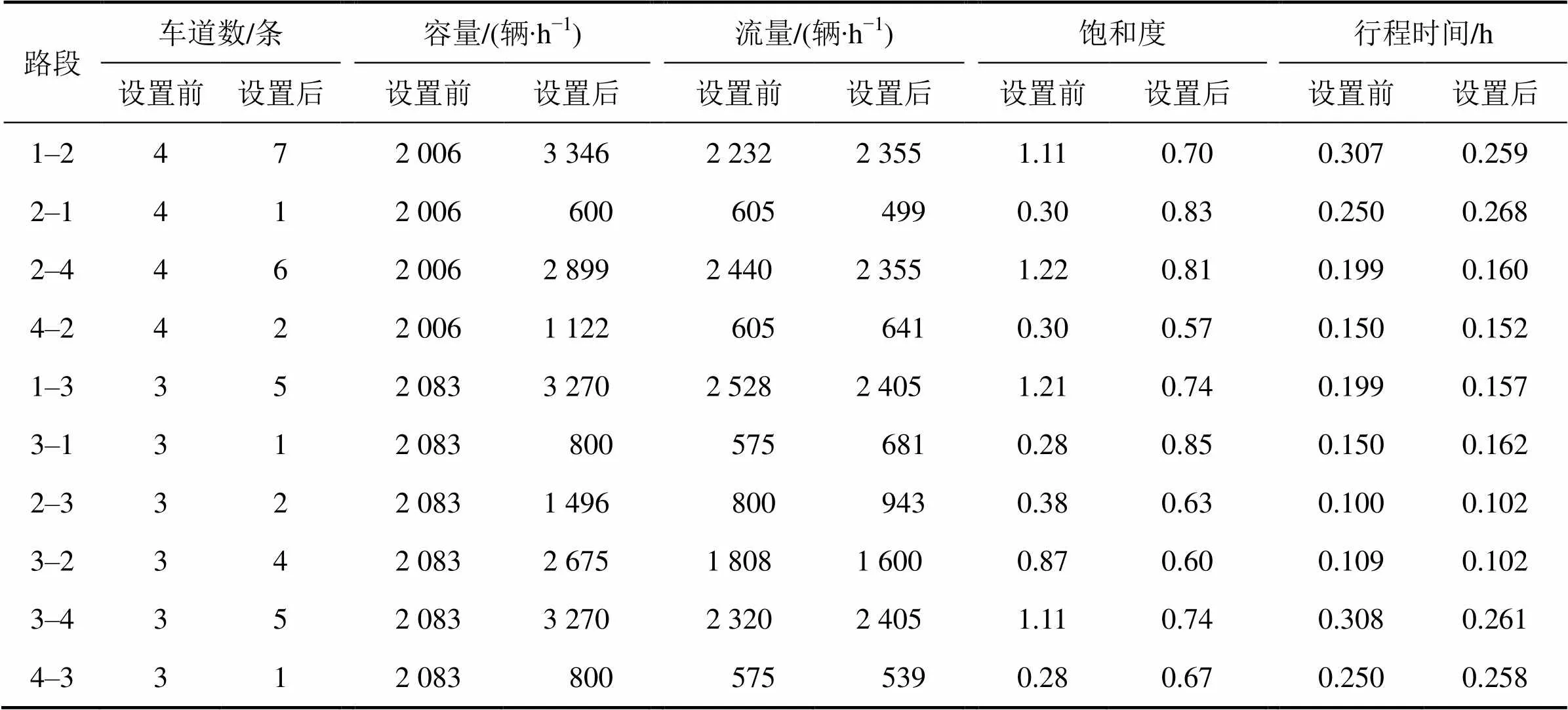
表4 路段特征值对比

算例结果也表明：虽然各路段流量随着车道数的调整发生变化，但路段流量不一定随着车道数的增加而增加，随着车道数的减少而减少，其原因在于用户的最短路择路特性。对OD对(1,4)而言，虽然路段1–3增加了2条车道，但路段1–2增加了3条车道，其所在路径的拥挤效应更低，分担了路段1–3所在路径的部分流量，最终导致路段1–3的车道数增加但流量有所下降。对于OD对(4,1)，虽然路段3–1减少了2条车道，但路段2–1减少了3条车道，其所在路径的拥挤效应更高，所以，路段2–1所在路径的部分流量转移到路段3–1所在路径，最终导致路段3–1的车道数减少但流量有所上升。

从OD对之间的均衡出行时间来看，虽然需求量较小的OD对(4,1)之间的出行时间由0.400 h上升到0.420 h，(2,3)之间的出行时间由0.100 h上升到 0.102 h，但需求量较大的OD对(1,4)之间的出行时间由0.506 h下降到0.419 h，(3,2)之间的出行时间也由0.109 h下降到0.102 h。这说明可变车道优化能够调用更多的道路资源给需求量较大的OD对之间的出行用户使用，使道路网络结构更好地匹配出行需求。

从OD对之间的总出行时间来看，虽然需求量较小的OD对(4,1)之间的总出行时间由472.000 h上升到495.600 h，(2,3)之间的总出行时间由80.000 h上升到81.600 h，但需求量较大的OD对(1,4)之间的出行时间由2 408.600 h下降到1 994.400 h，(3,2)之间的出行时间也由174.400 h下降到163.200 h。需求量较小的OD对之间的总出行时间增加幅度较小，需求量较大的OD对之间的总出行时间减少幅度较大，最终表现为系统总出行时间由3 135.000 h下降到2 735.000 h，降幅达12.76%，说明可变车道优化对降低系统总出行时间的效果明显。

5 结论

1) 从系统连通性层面出发，在轻交通流方向至少保留1条车道的前提下开展可变车道优化，从而保障了可变车道轻交通流方向路段的正常通行。

2) 考虑车辆换道对通行能力的影响，给出了平均车道利用系数计算公式。基于非均衡经济学理论的价格−数量调节，以系统总出行时间最小为目标构建了可变车道优化的混合整数双层规划模型，并采用粒子群优化算法对模型进行求解，验证了粒子群优化算法在该问题上的有效性和优越性。

3) 可变车道优化设置能调节交通流量在路网上的分布，均衡各路段的饱和度，降低重交通流方向路段的行程时间，但路段流量不一定呈现出随着车道数增加而增加，随着车道数减少而减少的规律。

4) 可变车道优化能够使道路网络结构更好地匹配城市居民出行需求，在道路资源一定的情况下有效地降低系统总出行时间，缓解因潮汐现象所导致的交通拥堵和道路资源闲置并存的问题。

[1] 荆敏. 市域轨道交通规划设计关键指标和主要运输组织模式研究[D]. 北京: 北京交通大学交通运输学院, 2016: 1. JING Min. Research on planning and designing key indicators and main transportation organization modes for regional rail transit[D]. Beijing: Beijing Jiaotong University. College of Transportation, 2016: 1.

[2] 王波. 上海轨道交通早高峰客流拥挤与居民通勤关系分析[J]. 城市轨道交通研究, 2016, 19(7): 75–78. WANG Bo. Relationship between the rush hour passenger flow congestion and residents commuting in Shanghai rail transit system[J]. Urban Mass Transit, 2016, 19(7): 75–78.

[3] 黄中祥, 蔡建荣, 吴立烜. 城市居民出行市场非均衡调控机制[J]. 长安大学学报(自然科学版), 2016, 36(6): 105–110. HUANG Zhongxiang, CAI Jianrong, WU Lixuan. Disequilibrium adjustment mechanism for urban resident travel markets[J]. Journal of Chang’an University(Natural Science Edition), 2016, 36(6): 105–110.

[4] SHEU J B, RITCHIE S. Stochastic modeling and real-time prediction of vehicular lane-changing behavior[J]. Transportation Research: Part B, 2001, 35(7): 695–716.

[5] WONG C K, WONG S C. Lane-based optimization of signal timings for isolated junctions[J]. Transportation Research Part B: Methodological, 2003, 37(1): 63–84.

[6] 马莹莹, 曾令宇, 陈纲梅, 等. 可变车道行驶方向的动态控制方法研究[J]. 控制理论与应用, 2016, 33(11): 1457–1462. MA Yingying, ZENG Lingyu, CHEN Gangmei, et al. Study on dynamic traffic control for reversible lanes[J]. Control Theory and Applications, 2016, 33(11): 1457–1462.

[7] JIANG Yinghong, BAO Lixia. Study on setting of variable lanes near intersection between one-way and two-way traffic[J]. Journal of Shanghai Jiaotong University, 2011, 45(10): 1562–1566.

[8] WOLSHON B, LAMBERT L. Reversible lane systems: synthesis of practice[J]. Journal of Transportation Engineering, 2006, 132(12): 933–944.

[9] WALECZEK H, GEISTEFELDT J, CINDRIC-MIDDENDORF D, et al. Traffic flow at a freeway work zone with reversible median lane[J]. Transportation Research Procedia, 2016, 15(6): 257–266.

[10] LAURENCE L, BRIAN W. Characterization and comparison of traffic flow on reversible roadways[J]. Journal of Advanced Transportation, 2010, 44(2): 113–122.

[11] DEY S, MA J, ADEN Y. Reversible lane operation for arterial roadways: The Washington, DC, USA Experience[J]. Institute of Transportation Engineers Journal, 2011, 81(5): 26–35.

[12] BEDE Z, PÉTER T. Optimal control with the dynamic change of the structure of the road network[J]. Transport, 2014, 29(1): 36–42.

[13] 陈坚, 霍娅敏. 典型潮汐车流路段可变车道设置方案研究[J]. 重庆交通大学学报(自然科学版), 2008, 27(6): 1127–1130. CHEN Jian, HUO Yamin. Study on setting design of variable lane on typical tide traffic road[J]. Journal of Chongqing Jiaotong University(Natural Science), 2008, 27(6): 1127–1130.

[14] 张卫华, 韩高峰, 颜冉, 等.城市道路路段可变车道设置效果评价方法[J]. 重庆交通大学学报(自然科学版), 2014, 33(4): 128–133. ZHANG Weihua, HAN Gaofeng, YAN Ran, et al. Evaluation on effect of setting variable lane in urban road section[J]. Journal of Chongqing Jiaotong University(Natural Sciences), 2014, 33(4): 128–133.

[15] 韩璧磷, 宋瑞, 何世伟.基于最小延误费用的可变车道数调整模型[J]. 道路交通与安全, 2009, 9(3): 1–5. HAN Bilin, SONG Rui, HE Shiwei. Variable lanes number adjustment model based on the smallest delay cost[J]. Road Traffic and Safety, 2009, 9(3): 1–5.

[16] 张鹏, 李文权, 常玉林. 可变车道的城市路网备用容量模型[J]. 西南交通大学学报, 2010, 45(2): 255–260. ZHANG Peng, LI Wenquan, CHANG Yulin. Reserve capacity model for urban road network with variable lanes[J]. Journal of Southwest Jiaotong University, 2010, 45(2): 255–260.

[17] 史峰, 苏焕银, 王雄.适用于路网潮汐流的可变车道设置方法研究[J]. 交通运输系统工程与信息, 2015, 15(4): 57–62. SHI Feng, SU Huanyin, WANG Xiong. Design of reversible lanes with tidal flow on road network[J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(4): 57–62.

[18] 高自友, 张好智, 孙会君.城市交通网络设计问题中双层规划模型、方法及应用[J]. 交通运输系统工程与信息, 2004, 4(1): 35–44. GAO Ziyou, ZHANG Haozhi, SUN Huijun. Bi-level programming models, approaches and applications in urban transportation network design problems[J]. Journal of Transportation Systems Engineering and Information Technology, 2004, 4(1): 35–44.

[19] 张好智, 高自友.可变车道的道路交通网络设计优化方法[J]. 中国管理科学, 2007, 15(2): 86–91. ZHANG Haozhi, GAO Ziyou. Optimization approach for traffic road network design problem[J]. Chinese Journal of Management Science, 2007, 15(2): 86–91.

[20] 杨小宝, 张宁, 关羽. 基于行为分析的道路通行能力中车道数因素研究[J]. 土木工程学报, 2009, 42(10): 104–110. YANG Xiaobao, ZHANG Ning, GUAN Yu. Behavior based analysis of the relationship between expressway capacity and number of lanes[J]. China Civil Engineering Journal, 2009, 42(10): 104–110.

[21] HOOSE H J. Planning effective reversible lane control[J]. Traffic Quarterly, 1963, 17(3): 408–413.

[22] HUANG Z X, HE G G. Disequilibrium transportation planning view[C]// WANG K C P, XIAO G P, JI J L. Proceedings of the 2nd International Conference on Transportation and Traffic Studies. Beijing: ASCE, 2000: 305–310.

[23] 徐慧智, 程国柱, 裴玉龙. 车道变换行为对道路通行能力影响的研究[J]. 中国科技论文, 2010, 5(10): 749–753. XU Huizhi, CHENG Guozhu, PEI Yulong. Study on effect of lane-changing behavioral characteristic to capacity[J]. Science Online, 2010, 5(10): 749–753.

[24] 杨小宝, 张宁. 道路通行能力中车道数因素的数学分析[J]. 武汉理工大学学报(交通科学与工程版), 2008, 32(4): 603–606. YANG Xiaobao, ZHANG Ning. Mathematical analysis of effects of lanes’ number on expressway capacity[J]. Journal of Wuhan University of Technology(Transportation Science & Engineering), 2008, 32(4): 603–606.

[25] 王炜, 过秀成. 交通工程学[M]. 南京: 东南大学出版社, 2009: 156. WANG Wei, GUO Xiucheng. Traffic engineering[M]. Nanjing: Southeast University Press, 2009: 156.

[26] 卢昌康, 冯刚, 王国海. 基于粒子群优化算法和Uniform LBP特征的分块跟踪[J]. 计算机工程与应用, 2016, 52(1): 200–205. LU Changkang, FENG Gang, WANG Guohai. Particle swarm optimization and uniform LBP-based algorithm for fragment tracking[J]. Computer Engineering and Applications, 2016, 52(1): 200–205.

[27] 程磊生, 吴志健, 彭虎, 等. 基于RDD的分布式粒子群优化算法[J]. 小型微型计算机系统, 2016, 37(11): 2542–2546. CHENG Leisheng, WU Zhijian, PENG Hu, et al. Distributed particle swarm optimization algorithm based on resilient distributed datasets[J]. Journal of Chinese Computer Systems, 2016, 37(11): 2542–2546.

Optimization of variable lane considering reduction of capacity

CAI Jianrong1, HUANG Ruqing2, HUANG Zhongxiang1

(1. School of Traffic and Transportation Engineering, Changsha University of Science & Technology, Changsha 410114, China;2. School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China)

In order to effectively alleviate the coexistence between traffic congestion and road resource idle caused by the tidal phenomenon, the variable lane optimization setting method was studied considering the influence of lane number on road unidirectional capacity. In this method, on the premise that the normal passage of the light traffic flow direction was ensured during the variable lane implementation process, the mixed integer bi-level programming model for variable lane optimization was established based on the price-quantity regulation of disequilibrium economic theory with the minimum total travel time of the system as the goal. Besides, the particle swarm optimization algorithm was used to solve the model, while the validity of the model and algorithm was verified by numerical examples. The results show that optimizing the variable lane setting from the system level can make full use of the idle road resources in the light traffic flow direction to improve the road capacity in the heavy traffic flow direction, which changes the travel time function, and then adjusts the redistribution of traffic flow on the road network and balances the saturation of each road, making the road network structure better match travel demands, and reducing the total travel time of the system economically and effectively in the case of specified road resources.

traffic engineering; tidal phenomenon; variable lane; bi-level programming; particle swarm optimization algorithm

10.11817/j.issn.1672-7207.2018.07.034

U491.2

A

1672−7207(2018)07−1838−07

2017−09−10；

2017−11−22

国家自然科学基金重点资助项目(51338002) (Project(51338002) supported by the Key Program of the National Natural Science Foundation of China)

黄中祥，教授，博士生导师，从事交通运输规划与管理研究；E-mail: mehzx@126.com

(编辑 陈灿华)