SVR响应面与进化多目标优化在结构设计中的应用

田昆，胡晓兵，赵清祥，徐营利



SVR响应面与进化多目标优化在结构设计中的应用

田昆，胡晓兵，赵清祥，徐营利

(四川大学 制造科学与工程学院，四川 成都，610065)

针对复杂结构优化设计中常出现的低效率、低精度问题，提出支持向量回归机(SVR)响应面与进化多目标优化算法相耦合的优化系统。基于结构风险最小化推导SVR响应面建立原理，采用具有异点预测值可对比特色的正交旋转组合设计作为样本点选取法，以获得最优试验区。基于NSGA-Ⅱ范式原理建立区间偏好进化优化算法并构建优化系统框架。以45 t门机主梁为研究对象，指定5个几何参数为设计变量，对最大位移、应力进行约束，以轻量化及首阶固有频率为双目标，利用所构建的优化系统进行优化求解。研究结果表明：主梁总质量减少15.9%，首阶固有频率减少9.2%。通过不同响应面模型的效果对比、灵敏度分析及优化方案检验，验证出优化系统的高效可行性。

支持向量回归机响应面；进化多目标优化算法；正交旋转组合设计；优化系统

在结构优化设计领域中，采取样本点、建立代理模型(响应面)、组建分析方法(优化算法)是三大关键环节。在对复杂的实际工程问题进行优化设计时常遇到以下阻碍：1) 试验设计样本点发生改变，常引起预测值方差发生改变，导致不同点间的预测值无法对比，难以得到最优试验区。2) 高度非线性问题对代理模型的拟合条件要求苛刻。3) 优化算法的选取或建立呈现多样化，从众多Pareto最优解集选取满意解的过程复杂且结果精度难以保证。针对实际工程问题，建立一种基于试验设计、响应面模型、进化优化算法相耦合的高效优化系统具有积极意义。近年来，一些国内外学者将工程优化技术应用到众多研究方向，ZHONG等[1]将Kriging响应面应用于跨声速翼型阻力系数模型的构建，得到了较好的非线性拟合效果，但响应值不可避免地存在陷入震荡或局部最优的可能。GOUDARZI等[2]采用支持向量机模型很好地解决了非线性定量结构拟合问题。QIAN等[3]通过对进化算法经典问题的深入分析，得出进化优化方法在可变方案问题中实施的高效性，对优化系统算法的建立具有一定参考价值。SUN等[4]将试验设计、响应面法、遗传算法结合，应用于自适应翼设计中，得到了满足条件的基线翼型板，建立了优化系统基本框架，但试验设计采点模块仍存在异点预测值无法对比的缺陷。本文作者着重建立SVR响应面与进化多目标优化算法相耦合的高效优化系统。从实际工程问题出发，首先推导出SVR响应面建立原理；其次，基于异点预测值可比性，采用正交旋转组合设计作为实验设计方法；再次，建立区间偏好进化优化算法并制定优化系统流程；最后，以门机主梁为研究对象，指定设计变量、约束条件及目标函数并基于组建的优化系统进行求解，通过不同响应面效果对比、灵敏度分析及优化方案验证，得出优化系统的高效可行性。

1 SVR响应面的提出

1.1 SVR响应面建立原理

(a) 带；(b) (x, y)损失值

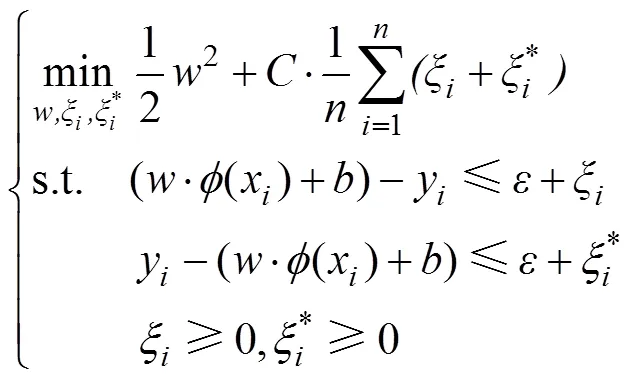
由Karush-Kuhn-Tucker(KKT)条件得：

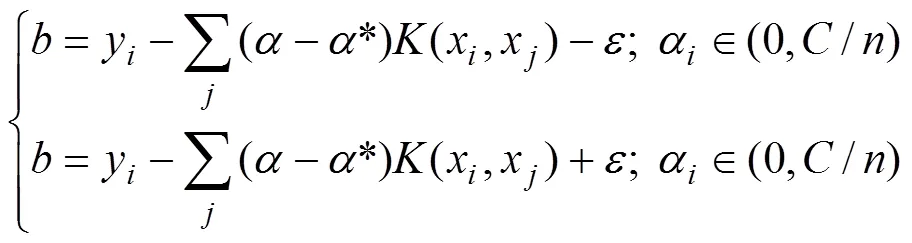
故决策函数可表达为

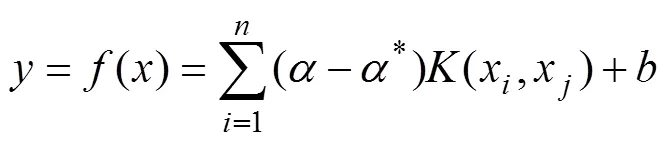
由此表明支持向量回归机的结构风险最小化较传统意义的经验风险最小化[8]有更精确的预测能力。

1.2 基于最优试验区的试验设计

选取试验点是构造响应面的前提，选取原则直接影响拟合精度。基于正交设计原理的D优化设计(D-optimal design)、中心复合实验设计(CCD)在流场翼型优化、加工中心多目标优化[9−10]等多领域范围的模型拟合上取得了较好效果。然而，若改变预测点，则这些方法下的预测值方差亦会改变，导致不同点间的预测值无法对比，难以得到最优试验区。

表1 二次回归正交旋转组合设计参数表

2 进化多目标优化求解

2.1 NSGA-Ⅱ范式基本问题

基于决策变量、目标函数、约束条件选择Pareto最优解集是多目标优化问题的核心。Pareto最优解集包含多个最优解，如何寻求一种方法可同时获取多个Pareto最优解以提高求解效率是近来多目标优化方法研究的热点。将多个候选解组成的种群嵌入到各代之间以实现全局搜索是进化优化方法的优势所在[12]，NSGA-Ⅱ[13]具有基于分层的迅速非被占优排序、紧促距离下同序值进化个体的对比、精英保留等突出特色，是一种优秀的进化多目标优化方法。

NSGA-Ⅱ执行流程大致分为三步：首先，随机性构造一初始种群，同时将其作为第一代父代种群；其次，经选择及交叉变异后产生一过渡种群，将其与当前种群进行组合并进行组合后的进化个体排序；最后，依序从组合后种群中选取进化个体作为下一代种群，当种群规模达到时为止。

不难证明，应用NSGA-Ⅱ可找出分布均匀、拟合性及延伸性好的Pareto最优解集。然而，现实中太多优化解可能造成用户选择疲劳及工效降低，如何基于NSGA-Ⅱ范式基本原理寻求改进的进化优化方法很有必要。

2.2 区间偏好进化优化及算法

区间偏好进化优化方法旨在将个人偏好融入进化多目标优化过程，以期在提高工效的基础上获取性能更优的最优解[14]。该方法优势在于：基于NSGA-Ⅱ范式基本原理进行大的种群进化以增强搜索性能；将相似度策略用于评价种群进化个体的相关指标，避免用户疲劳；通过区间衡量各指标的偏好，基于求解优化精确区间偏好；基于同一序值进化体的不同满意度诱使种群向偏好区进化。

方法执行路线描述为：1) 获取用户对不同指标的偏好；2) 用户对基于K-均值聚类法获取的进化种群分类中心进行评价[15]，并通过计算机算得进化种群个体的指标值；3) 基于已有的分类中心评价值，对其他种群个体的指标值进行估算；4) 精确化偏好区间并对种群个体排序，诱使种群向偏好区域搜索。

依据方法特点及执行路线组建算法，如图2所示，具体步骤为：

1) 获取种群进化的相关参数进而生成原始种群；

2) 针对指标项指定用户偏好区；

3) 基于K-均值聚类法分离种群；

4) 进行进化解码并通过计算机获取个体指标，进而组成进化体的区间矢量；

5) 精确偏好区间，基于NSGA-Ⅱ范式进行遗传以获得下一代种群；

6) 算法若达到要求条件则输出优化结果，否则，判断偏好是否改变，若改变则转向步骤2)，若无变化则转向步骤3)。

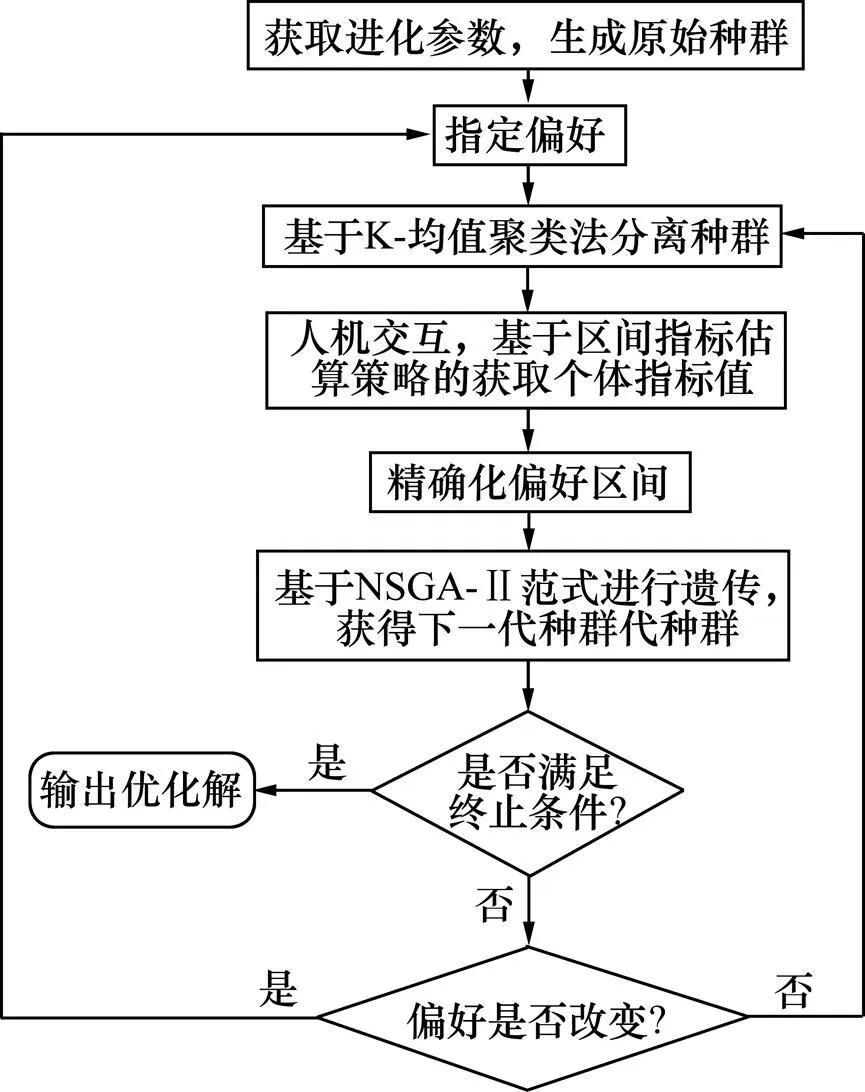
图2 进化优化算法流程图

2.3 SVR响应面耦合进化优化的流程

采用正交旋转试验设计获取样本点，基于SVR响应面理论建立数学模型，得到耦合进化优化算法的优化系统流程，如图3所示。

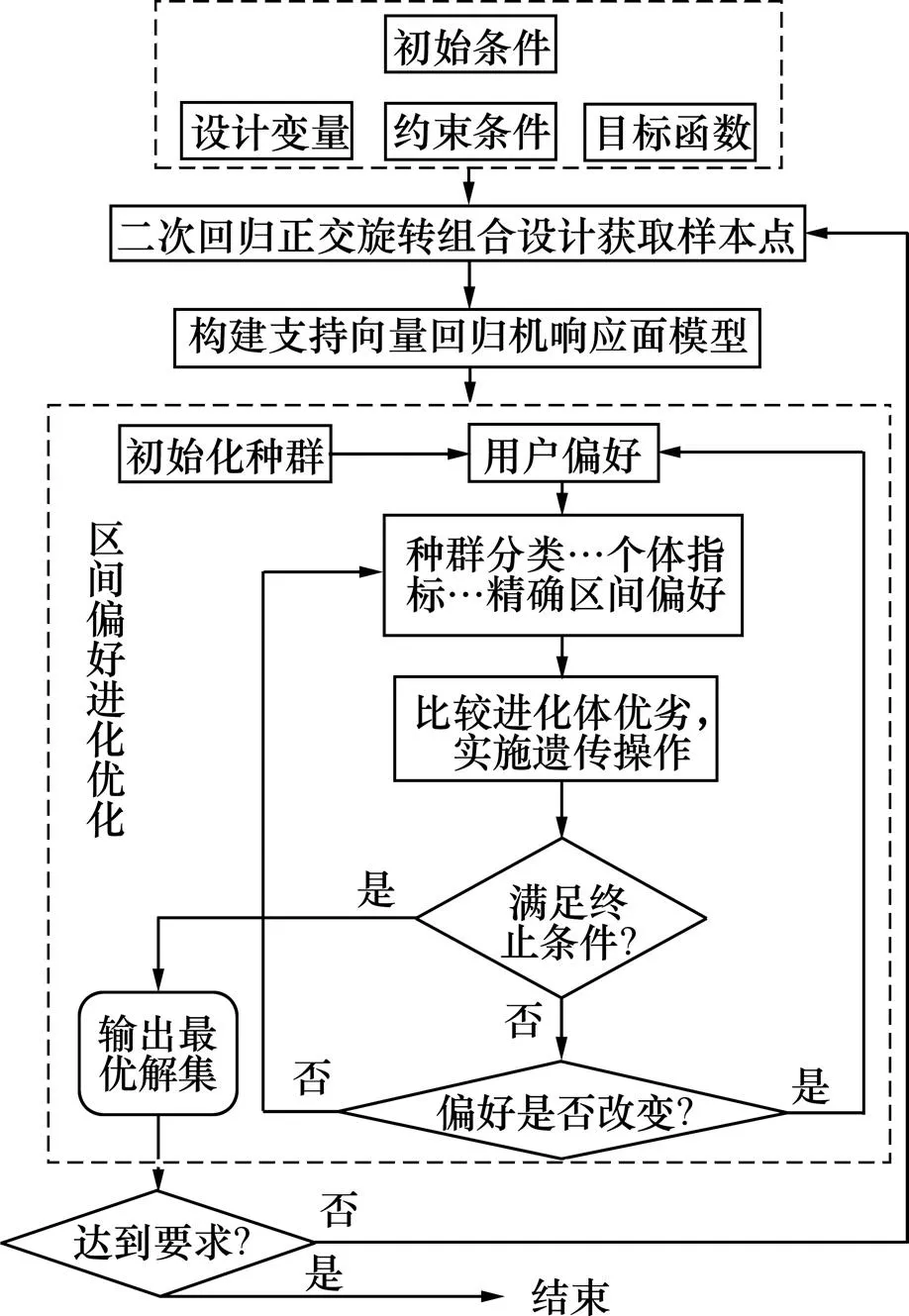
图3 优化系统流程图

3 算例：门机主梁多目标优化

3.1 门机主梁优化模型建立

图4所示为45 t门机整体CAD模型及主梁截面示意图，门机相关参数见表2(其中门机主梁参数1为总高度，2和3分别为主梁内、外腹板厚度，4和5分别为上、下翼缘板厚度)。

(a) 门机模型；(b) 主梁截面图

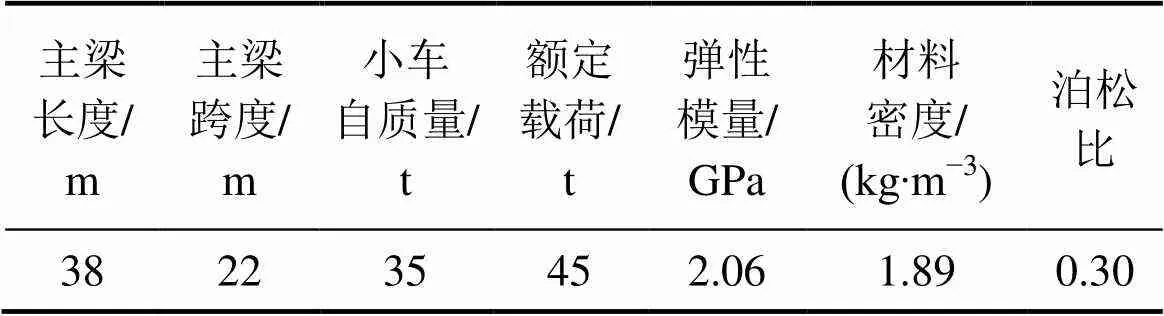
表2 门机主要参数

门机主梁多目标优化设计首先指定目标函数，将主梁轻量化及首阶固有频率远离震源频率作为双优化目标，确定目标函数为

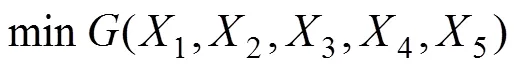
主梁是门机结构的主要承载部位，在对主梁的质量及首阶频率优化时，会造成挠度、应力发生变化。为保证优化效果，引入约束条件：

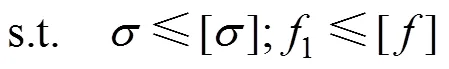
3.2 SVR响应面模型的建立

通过试验设计选取样本点是建立响应面模型的前提，基于二次回归正交旋转组合设计，门机主梁优化设计中含有5个设计变量(5因素)，由表1选用5因素对应之下的各参数值，依据相应编码表进行59次试验，如表4所示。

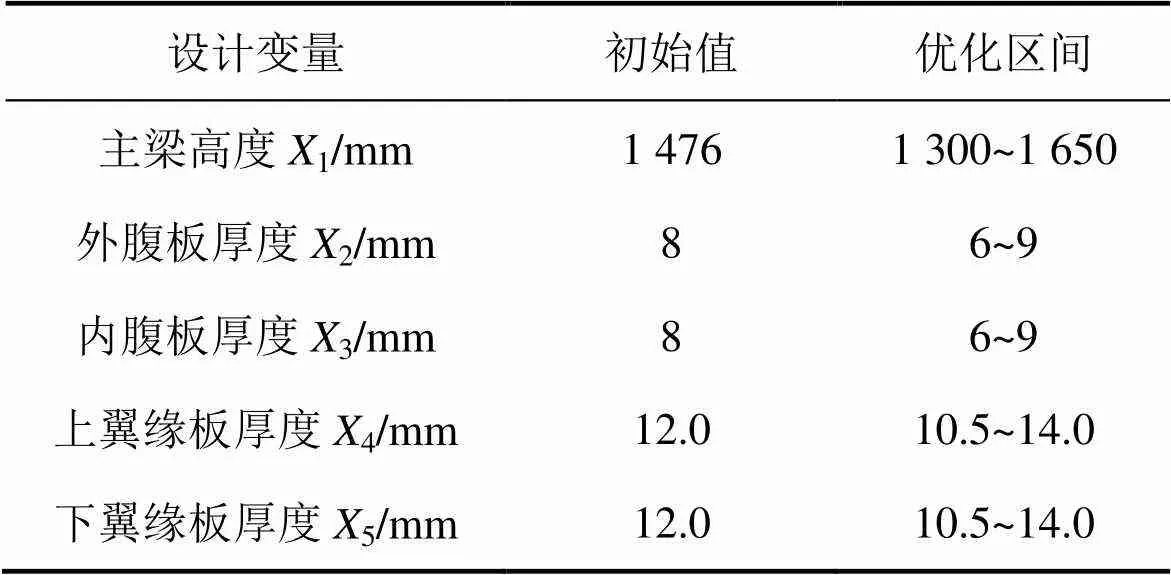
表3 主梁设计变量取值范围

基于已选设计点，采用支持向量机的方法实现对各输出量的响应面拟合，建立SVR响应面。如图5所示，分别为设计变量对质量、首阶固有频率、最大等效应力、最大位移的响应。为加强可比性，将基于二次回归正交旋转组合设计建立的SVR响应面与采用中心复合试验设计(CCD)建立的多项式响应面、Kriging响应面相对比(如表5所示)，通过响应时间、均方根误差及确定性系数等参数的分析(其中拟合精度与确定性系数、均方根误差成正相关)，可得出SVR响应面具有效率高、拟合精度高等突出优势。

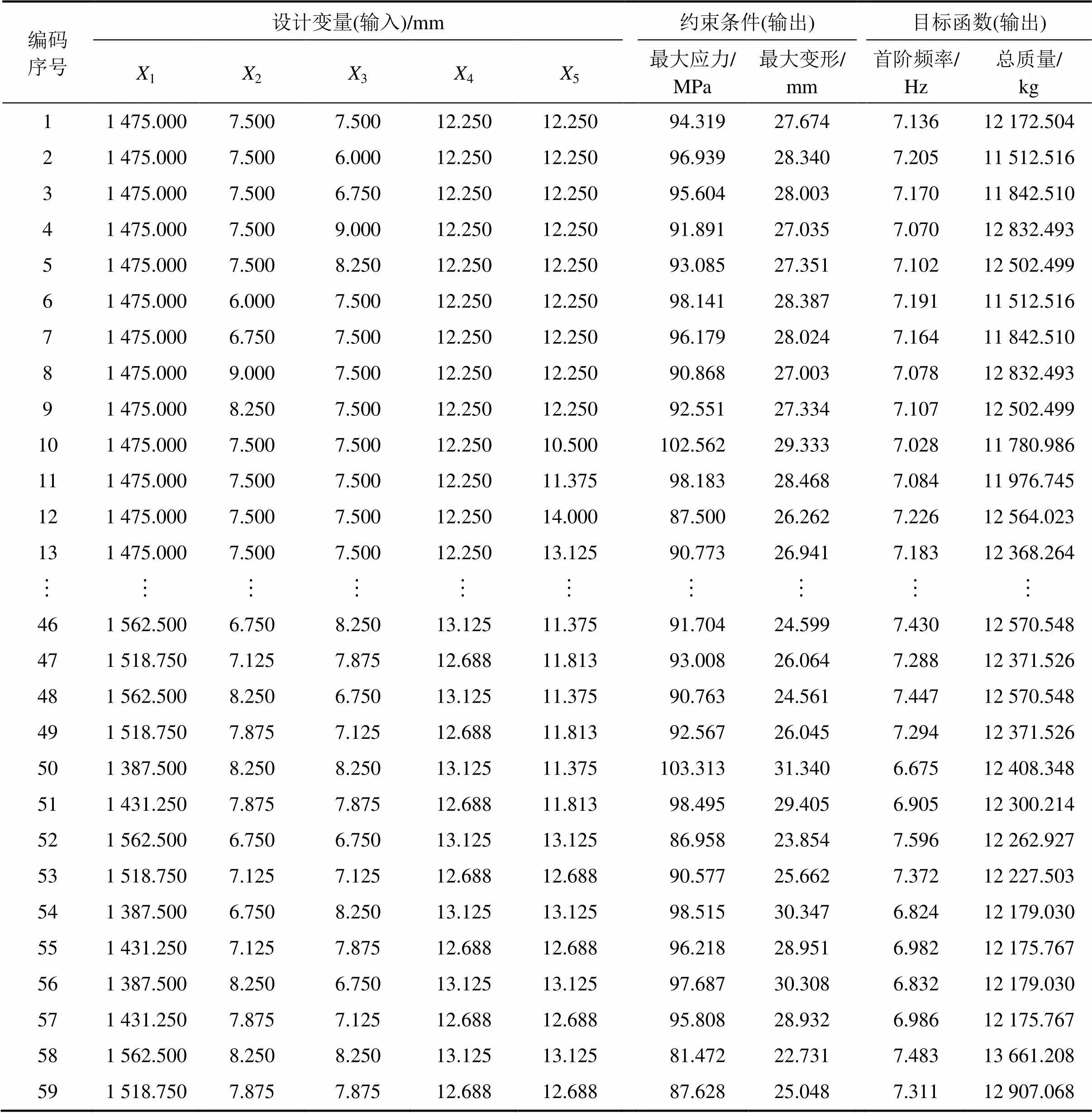
表4 二次回归正交旋转组合设计试验

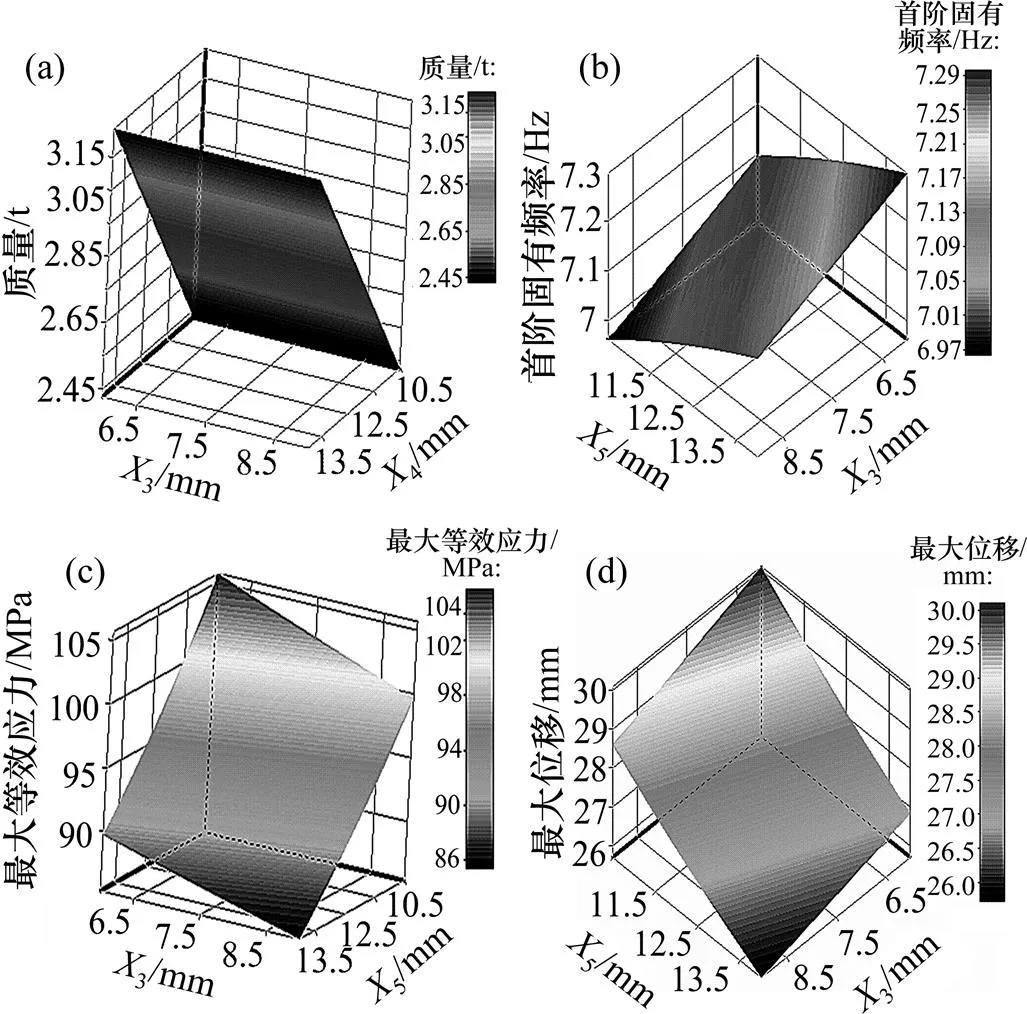
(a) 质量响应面；(b) 频率响应面；(c) 应力响应面；(d) 位移响应面

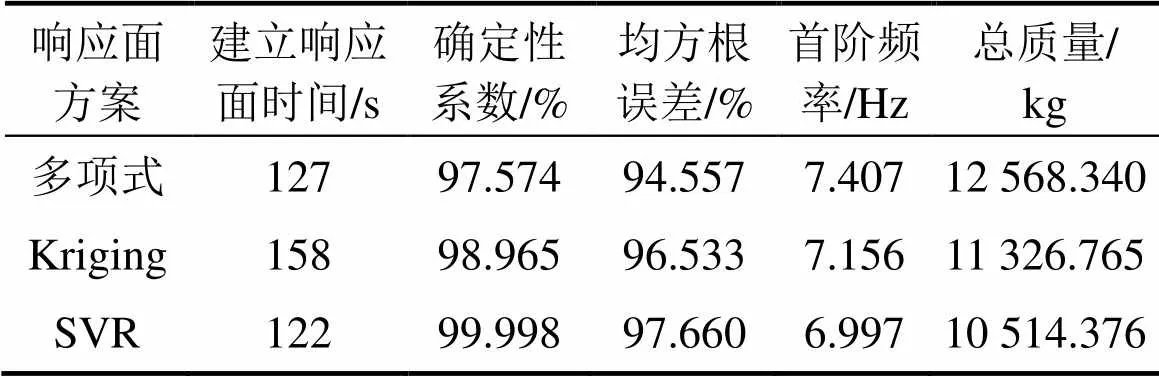
表5 不同响应面拟合精度及优化结果

3.3 灵敏度分析

在门机主梁优化过程中，为体现设计变量与各输出量间的相关性，需要进行灵敏度分析。采用灵敏度分析可找出结构响应敏感参数及可忽略的不显著元素，对减少设计变量、提高优化效率有积极意义。输出量灵敏度分析结果如图6所示。若设计变量位于正半轴，则表征响应区与设计变量成正相关，反之成负相关，矩形高度表示设计变量对响应的影响程度。在频率区中，首阶固有频率随设计变量1，5和4的增大(减小)而增大(减小)，随3和2的增大(减小)而减小(增大)，影响程度依据矩形高度依次降低。其他分析与此类似。

图6 输出量灵敏度分析结果

3.4 优化及验证

通过SVR响应面模型与进化优化算法构成的优化系统对门机主梁进行优化求解，选取轻量化为主导偏好得到优化方案见表6。分析优化结果可知：方案1最佳，与门机主梁初始质量12 503.5 kg、首阶固有频率7.705 Hz相比，经进化多目标优化后，在满足各约束条件的前提下，总质量减少15.9%，首阶固有频率减少9.2%，主梁整体达到最优。

为验证优化系统的高精度性，基于优化方案1建立主梁CAD模型，通过ANSYS软件进行有限元分析，得到主梁等效应力云图及位移云图，如图7所示。从图7可见：主梁最大应力为107.24 MPa，最大位移为30.406 mm，对比方案1中相应结果可知误差均在0.025以内。

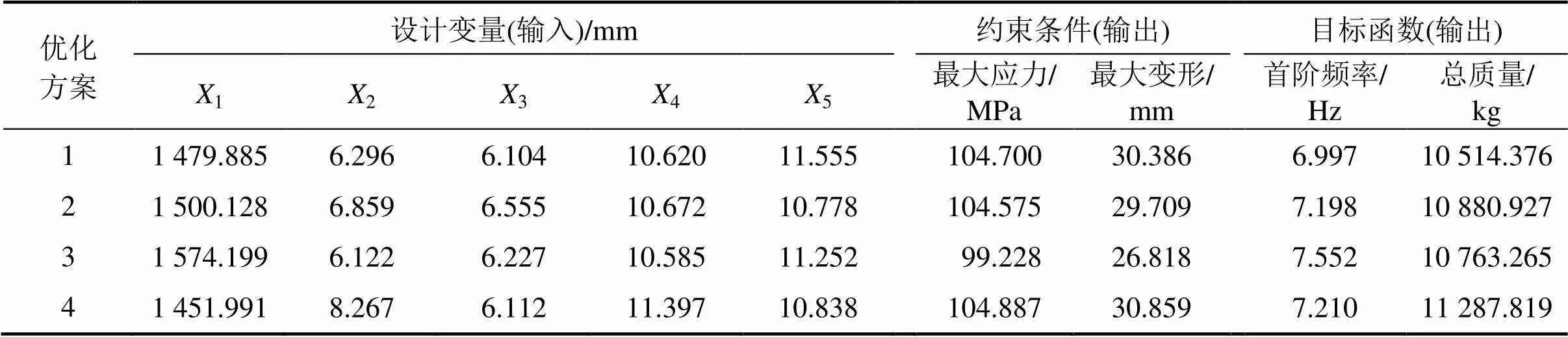
表6 主梁优化解集

(a) 等效应力验证云图；(b) 位移验证云图

4 结论

1) 基于结构风险最小化原理推导了SVR响应面构造理论，采用二次回归正交旋转组合设计试验很好解决了异点预测值的对比问题，可获得高质量样本点。为组建高效代理模型提供了理论依据。

2) 基于NSGA-Ⅱ范式，建立了区间偏好进化多目标优化算法，与正交旋转组合试验设计、SVR响应面理论相耦合，建立了结构优化系统框架。

3) 将优化系统应用于门机主梁的多目标优化设计中，建立了主梁SVR响应面模型，经多方法对比及灵敏度分析，体现了优化系统的高效性。采用区间偏好进化优化算法对响应面模型进行优化求解，得到主梁总质量减少15.9%、首阶固有频率减少9.2%的最优方案，并采用有限元法验证了优化系统的高精度性。

[1] ZHONG Xiaoping, DING Jifeng, LI Weiji, et al. Robust airfoil optimization with multi-objective estimation of distribution algorithm[J]. Chinese Journal of Aeronautics, 2008, 21(4): 289−295.

[2] GOUDARZI N, ARABCHAMJANGALI M, AMIN A H. Calculation of hildebrand solubility parameters of some polymers using QSPR methods based on LS−SVM technique and theoretical molecular descriptors[J]. Chinese Journal of Polymer Science, 2014, 32(5): 587−594.

[3] QIAN Chao, YU Yang, ZHOU Zhihua. Variable solution structure can be helpful in evolutionary optimization[J]. Science China (Information Sciences), 2015, 58(11): 1−17.

[4] SUN Rujie, CHEN Guoping, ZHOU Chen, et al. Multidisciplinary design optimization of adaptive wing leading edge[J]. Science China Technological Sciences, 2013, 56(7): 1790−1797.

[5] 唐应时, 朱彪, 朱位宇, 等. 基于响应面方法的转向梯形优化设计[J]. 中南大学学报(自然科学版), 2012, 43(7): 2601−2606. TANG Yingshi, ZHU Biao, ZHU Weiyu, et al. Optimization of ackerman steering linkage based on RSM[J]. Journal of Central South University(Science and Technology), 2012, 43(7): 2601−2606.

[6] 白鹏, 张喜斌, 张斌. 支持向量机理论及工程应用实例[M]. 西安: 西安电子科技大学出版社, 2008: 13−15. BAI Peng, ZHANG Xibin, ZHANG Bin. Support vector machine theory and engineering application examples[M]. Xi’an: Xidian University Press, 2008: 13−15.

[7] 邓乃扬, 田英杰. 支持向量机: 理论、算法与拓展[M]. 北京: 科学出版社, 2009: 77−80. DENG Naiyang, TIAN Yingjie. Support vector machine: theory, algorithm and extension[M]. Beijing: Science Press, 2009: 77−80.

[8] 熊盛武, 刘宏兵, 陈琼, 等. 多目标粒度支持向量机理论及其应用[M]. 北京: 科学出版社, 2014: 203−206. XIONG Shengwu, LIU Hongbing, CHEN Qiong, et al. Multi-objective particle size support vector machine theory and its application[M]. Beijing: Science Press, 2014: 203−206.

[9] 李沛峰, 张彬乾, 陈迎春. 基于响应面和遗传算法的翼型优化设计方法研究[J]. 西北工业大学学报, 2012, 30(3): 395−401. LI Peifeng, ZHANG Binqian, CHEN Yingchun. Optimization of airfoil design based on response surface and genetic algorithm[J]. Journal of Northwestern Polytechnical University, 2012, 30(3): 395−401.

[10] 姜衡, 管贻生, 邱志成, 等. 基于响应面法的立式加工中心动静态多目标优化[J]. 机械工程学报, 2011, 47(11): 125−133. JIANG Heng, GUAN Yisheng, QIU Zhicheng, et al. Dynamic and static multi-objective optimization of a vertical machining center based on response surface method[J]. Journal of Mechanical Engineering, 2011, 47(11): 125−133.

[11] 杨德. 试验设计与分析[M]. 北京: 中国农业出版社, 2002: 234−246. YANG De. Experimental design and analysis[M]. Beijing: China Agriculture Press, 2002: 234−246.

[12] BUI L T, DEB K, ABBASS H A, et al. Interleaving guidance in evolutionary multi-objective optimization[J]. Journal of Computer Science and Technology, 2008, 23(1): 44−63.

[13] HUANG Renfang, LUO Xianwu, JI Bin, et al. Multi-objective optimization of a mixed-flow pump impeller using modified NSGA−II algorithm[J]. Science China Technological Sciences, 2015, 58(12): 2122−2130.

[14] DEB K, KSALAN M. Guest editorial: special issue on preference-based multiobjective evolutionary algorithms[J]. IEEE Transactions on Evolutionary Computation, 2010, 14(5): 669−670.

[15] LU Zhimao, LIU Chen, MASSINANKE S, et al. Clustering method based on data division and partition[J]. Journal of Central South University, 2014, 21(1): 213−222

Application of SVR response surface coupling evolutionary multi-objective optimization algorithm to structural optimization

TIAN Kun, HU Xiaobing, ZHAO Qingxiang, XU Yingli

(School of Manufacturing Science and Engineering, Sichuan University, Chengdu 610065, China)

Aiming at the low efficiency and low precision in complex structure optimization design, an optimization system with support vector regression(SVR) response surface coupled with evolutionary multi-objective optimization algorithm was proposed. Based on structural risk minimization, the principle of SVR response surface was deduced. Orthogonal rotation combination design with contrasting predictive value was used to select sampling points to obtain the optimal experimental area. Based on the principle of NSGA-Ⅱ paradigm, the evolutionary optimization algorithm of interval preference was established and the optimization system framework was constructed. Taking the main girder of 45 t gantry crane as the research object, five geometrical parameters were adopted as design variables, and the maximum displacement and stress were constrained. The results show that by using the optimized system, the total mass of main girder and the first-order natural frequency are decreased by 15.9% and 9.2%, respectively. The high efficiency and feasibility of the optimization system are proved by the comparison of the results of different response surface models, the sensitivity analysis and the optimization scheme validation.

support vector regression response surface; evolutionary multi-objective optimization algorithm; orthogonal rotation combination design; optimization system

10.11817/j.issn.1672-7207.2018.07.011

TH213

A

1672−7207(2018)07−1650−07

2017−07−16；

2017−09−12

四川省科技计划项目(2015GZ0014，2016GZ0169，2017GZ0146) (Projects(2015GZ0014, 2016GZ0169, 2017GZ0146) supported by the Science and Technology Program of Sichuan Province)

胡晓兵，博士，教授，从事CAD/CAPP/CAM、数字化车间、自动化控制、企业信息化研究；E-mail: huxb@scu.edu.cn

(编辑 杨幼平)