地面堆载引起下卧盾构隧道剪切错台变形计算研究

魏纲，俞国骅，洪文强



地面堆载引起下卧盾构隧道剪切错台变形计算研究

魏纲1，俞国骅2，洪文强3

(1. 浙江大学 城市学院土木工程系，浙江 杭州，310015；2. 安徽理工大学 土木建筑学院，安徽 淮南，232001；3. 浙江大学 岩土工程研究所，浙江 杭州，310058)

采用Boussinesq公式求解得到地面堆载工况下隧道轴线处的土体附加应力；基于剪切错台模型，运用最小势能原理计算得到下卧地铁盾构隧道的纵向位移以及相邻盾构衬砌环之间的错台量和环间剪切力。通过算例分析，研究堆载面荷载、堆载偏移距离、隧道上部覆土厚度以及堆载尺寸和对隧道纵向位移的影响。研究结果表明：越大，盾构隧道的沉降量就越大，但隧道沉降影响范围并没有增大；随着增大，隧道沉降量越来越小且沉降量减小的速率加快，隧道的水平位移则先增大后减小；随着增加，隧道最大沉降减小，同时隧道沉降影响范围加大；的改变对隧道竖向位移影响非常小，的改变对隧道沉降量及范围的影响较大；隧道的竖向位移要明显大于隧道的水平位移。

地面堆载；盾构隧道；剪切错台；隧道纵向位移

建设城市轨道交通是缓解城市交通压力的有效途径。但随着城市运营地铁的增多，临近工程建设活动对既有地铁盾构隧道的不利影响也越来越显著。例如盾构隧道上方有地面堆载时，原有受力平衡会被打破，引起盾构隧道应力重分布[1]，产生过大的横向或者纵向变形，导致管片开裂、接缝张开、螺栓失效等现 象[2]，对地铁安全产生影响。因此，研究上部地面堆载对临近既有盾构隧道的影响具有重要意义。国内外关于地面堆载对既有盾构隧道影响的研究方法可归纳为现场实测法[2−5]、理论计算法[6−8]、数值分析法[9−10]和室内模型试验法[11−12]等。在理论计算研究方面，李春良等[6]基于弹性地基梁理论建立了地面荷载作用下的盾构隧道结构纵向内力计算模型，得到盾构隧道在地面荷载作用下的附加沉降变形和内力；姜启元等[7]对盾构隧道因地面堆载引起的隧道纵向变形进行了力学分析，利用弹性地基梁理论求得隧道断面受力；侯芳[8]将软土盾构隧道简化为无限长弹性地基梁，推导了均布荷载作用下无限长地基梁解析解的表达式。以上方法均基于弹性地基梁法，将盾构隧道简化为均质弹性梁，未考虑隧道环间的“接头效应”，无法计算管片错台量，与实际情况有所出入。因此需进行进一步研究。本文作者利用王如路[13]提出的“剪切错台模型”，将盾构隧道等效为1个由剪切弹簧连接的弹性地基短梁，运用最小势能原理计算地面堆载引起下卧盾构隧道的纵向变形，以及相邻隧道环之间的错台量和环间剪切力，评估盾构隧道在运营期间的结构安全性和抗渗性。

1 地面堆载引起的隧道附加应力计算

首先建立地面堆载力学计算模型。如图1所示，临近地铁隧道有一矩形地面堆载，荷载为，长为，宽为。以地面堆载中心为原点，取平行隧道方向为轴，垂直盾构隧道方向为轴。盾构隧道轴线处埋深为，隧道上部覆土厚，隧道外径为，堆载中心离隧道轴线的水平距离为。

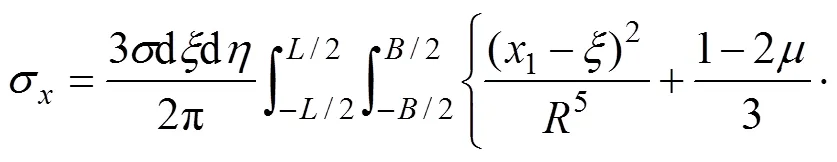
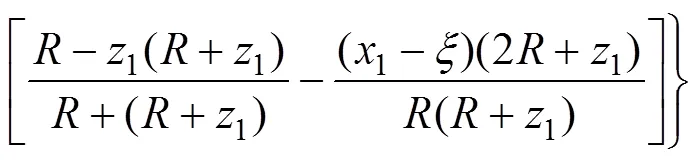
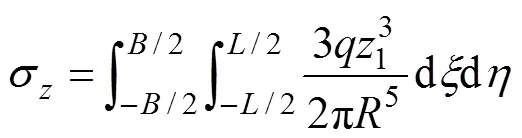
(a)平面图；(b) 横截面图

图1 计算模型平面图和横截面图

Fig. 1 Span and cross-section view of calculation model

2 基于最小势能原理计算隧道纵向变形

2.1 盾构隧道与土体相互作用分析

在分析盾构隧道与土体相互作用时，假定：将盾构隧道衬砌环视为由剪切弹簧连接的弹性地基短梁，地面堆载导致隧道以环间剪切错台的方式进行变形，见图2。梁发云等[14−15]验证了该模型的合理性。

图2 盾构隧道环间错台变形示意图

2.2 运用能量变分法计算隧道纵向位移

2.2.1 盾构隧道的总势能

刘晓强等[16]基于最小势能原理将能量变分法应用于隧道开挖引起的地下管线响应，该方法求解简便，容易达到要求精度。本文将这种能量变分法运用到计算地面堆载引起临近盾构隧道纵向位移的问题中。

任取盾构隧道一环进行分析，编号为，其所受到的水平荷载F为

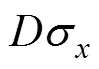
同理可得到盾构隧道的竖向荷载F为

2.2.2 假设隧道衬砌环的位移函数

能量变分解法原理，是假定合适的位移函数来表示盾构隧道受地面堆载影响的基本变形形状。本文假设隧道位移函数[16]如下，并按傅里叶级数展开。隧道的水平位移函数为

隧道的竖向位移函数为

2.2.3 变分控制方程

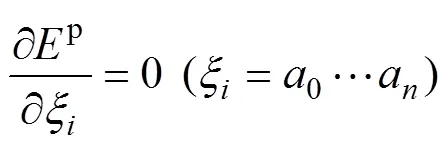
对式(8)求解，可得隧道水平位移控制方程为

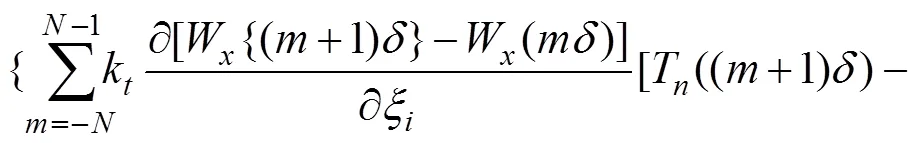
同理，可得隧道竖向位移的控制方程为

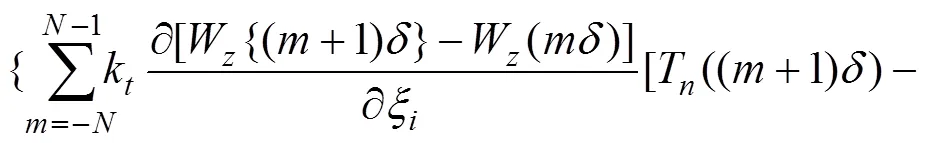
将式(10)表达为矩阵形式：

式中：[t]为隧道环间刚度矩阵，

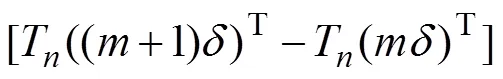
[s]为土体刚度矩阵，

由式(11)计算可得到待定系数矩阵，再代入假设的隧道位移函数()即式(6)和 (7)，可以得到地面堆载作用引起的盾构隧道纵向位移。

相邻盾构管片之间的位移差值即为错台量∆，其中隧道的水平错台量为

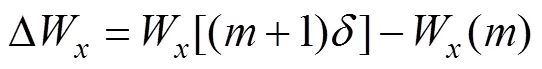
隧道的竖向错台量为

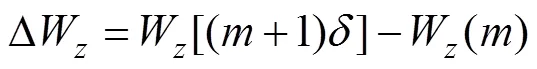
相邻盾构管片环之间的水平剪切力为

隧道的竖向剪切力为

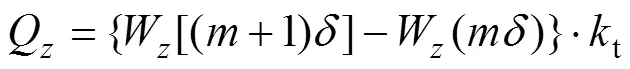
取10阶的刚度矩阵[p]和[t]即可满足计算精度，以上算法通过Matlab编程进行数值计算。

3 工程案例分析

选取戴宏伟等[9]提出的临近隧道的地面堆载工程作算例分析。分别采用本文方法、有限差分法[9]以及弹性地基梁法[19]计算得到盾构隧道纵向位移曲线，并进行对比，以验证本文方法的正确性。

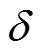
图3所示为该算例工况采用3种方法计算得到的纵向隧道竖向位移曲线，图3中竖向位移负值代表沉降，正值代表隆起，以下同。从图3可知：本文方法与有限差分法[9]计算得到的隧道沉降量在数值和趋势上都较吻合，最大沉降量分别为25.1 mm和25.2 mm，已超过相关管理条例[20]规定的地铁结构最终绝对位移限值20 mm。弹性地基梁法[19]在(−80，−55) m和(55，80) m 2个区间内与其他2个方法的计算数值都较为吻合，但在(−30，30) m区间内沉降量迅速增加，最大沉降量达到31.8 mm。

本文方法相对于其他2种方法，还能够计算得到相邻盾构环之间的错台量和环间剪切力，见图4和图5。图4所示为本文方法计算得到的管片竖向错台量。从图4可知：在隧道沉降曲线反弯点处的管片错台量最大，达到0.5 mm。参考上海盾构隧道错台等级划分标准[21]，该错台量的评价等级为Ⅱ级，没有超过4 mm的控制标准，但隧道结构的安全性和抗渗性均有所降低，应该加强监测；在隧道沉降量最大点处的管片错台量接近0 mm，表明隧道沉降量最大点附近相邻盾构环之间几乎不发生错台变形。

图5所示为本文方法计算得到的隧道竖向环间剪力。从图5可知：盾构隧道环间剪力值的变化规律与管片错台量的变化规律一致，隧道沉降量最大值处的环间剪力接近0 kN；在隧道沉降曲线反弯点处的剪力最大，为200 kN。本工程中相邻隧道环之间用17颗M30螺栓连接，其剪切强度极限为665.36 kN，计算得到的最大剪力没有超过该极限值。

1—有限差分法；2—本文方法；3—弹性地基梁法。

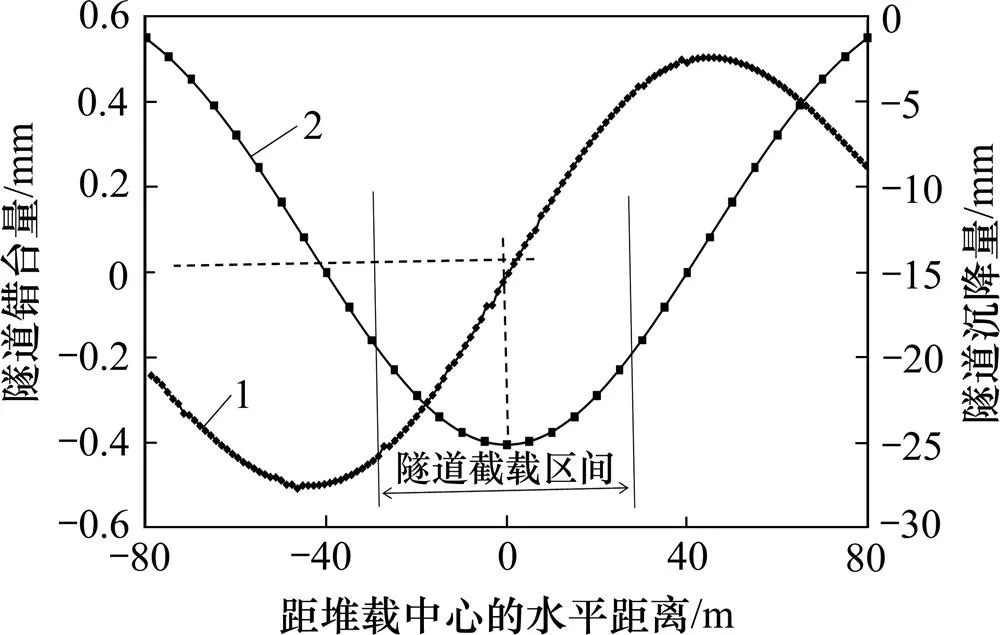
1—盾构隧道错台量；2—隧道沉降量。

图5 盾构隧道环间剪力值

4 隧道纵向位移的单因素影响分析

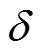
为了更为直观分析且计算相对简便，本文将进行单因素影响分析。

4.1 堆载偏移距离s改变对隧道变形的影响

在标准工况下，仅改变地面堆载的位置(堆载=100 kPa和面积不变)，以堆载中心在横向上离隧道中心的距离为控制变量。分别取为0，5，10，15，20，25，40，60和80 m等工况，来研究改变对隧道变形的影响规律。

4.1.1 隧道竖向位移影响规律

图6所示为不同时计算得到的盾构隧道竖向位移变化曲线。从图6可知：1) 在地面堆载作用下盾构隧道竖向变形曲线呈中间沉降、两端略有隆起的规律，沉降段大致呈正态分布，影响范围(−80，80) m较大；2) 随着逐渐变大，隧道的沉降逐渐变小；隧道影响范围内中部沉降量变化大，两端变化小。隧道变形的影响范围则基本不变。

偏移距离s/m：1—0；2—5；3—10；4—15；5—20。

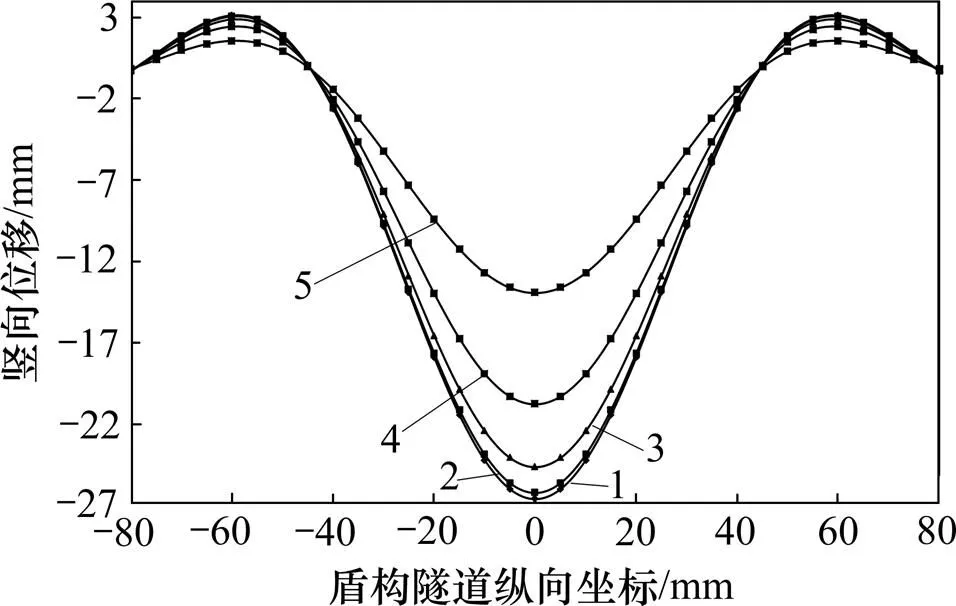
图7所示为盾构隧道中心点(=0 m处)最大沉降随改变的曲线。从图7可知：当=0 m时隧道最大沉降量为−26.62 mm；随着变大，最大沉降逐渐变小；当=20 m时隧道最大沉降量为−13.93 mm，比=0 m时减少了12.69 mm。原因是堆载位置偏离，隧道在竖直方向上受到的附加作用力逐渐减小，从而使得隧道竖向沉降量变小；当＞16 m时，隧道沉降量就小于20 mm，处于安全范畴。另外偏移距离在(0，10) m范围变化时，隧道最大沉降变化量为1.97 mm，但偏移距离在(10，20) m范围变化时，隧道最大沉降变化量达到10.72 mm，即随着偏移距离的增大，隧道最大沉降值的变化率加大。戴宏伟等[9]在分析堆载位置对隧道最大变形的影响时，也获得了类似的特征曲线，结论与本文的类似。

图7 不同s时盾构隧道最大沉降量变化图

4.1.2 隧道水平位移影响规律

图8所示为不同时计算得到的隧道水平向位移曲线，图8中水平位移正值代表隧道向远离堆载方向移动。从图8可见：1) 当=0 m时，隧道的水平向位移值几乎为0；2) 当=5 m时，隧道的水平向位移迅速增大。当=15 m时，隧道水平位移达到最大，最大水平位移为3.5 mm。中心处水平位移增幅最大，整体呈对称的正态分布曲线。3) 随着继续增大，隧道的水平位移则开始逐渐减小，曲线呈整体减小趋势，最终接近0 m。

图9所示为隧道中心点(=0 m)的水平位移随改变的曲线，图10所示为=80 m处隧道的水平位移随改变的曲线。从图9和图10可知：=0 m处隧道的水平位移与=80 m处隧道的水平位移的变化规律一致，均呈现先增大、后减小的规律；当=15 m时隧道的水平位移达到最大，最大值分别为3.5 mm和1.7 mm；当=80 m时，隧道的水平位移接近0 mm。其原因是：当=0 m时，隧道在水平方向受力平衡，所以，隧道水平向位移趋向于0 mm；当地面堆载位置偏移后，打破了隧道在水平方向的受力平衡状态，隧道在水平方向受到附加力作用，导致隧道产生远离堆载方向的水平向位移；当隧道偏移到一定位置处(= 15 m)，隧道受到的附加力达到最大；随着隧道位置继续外移，该附加力逐渐减小，使隧道在水平向的受力状态又逐渐趋向于受力平衡状态。

偏移距离s/m：1—0；2—5；3—10；4—15；5—20；6—40；7—60。

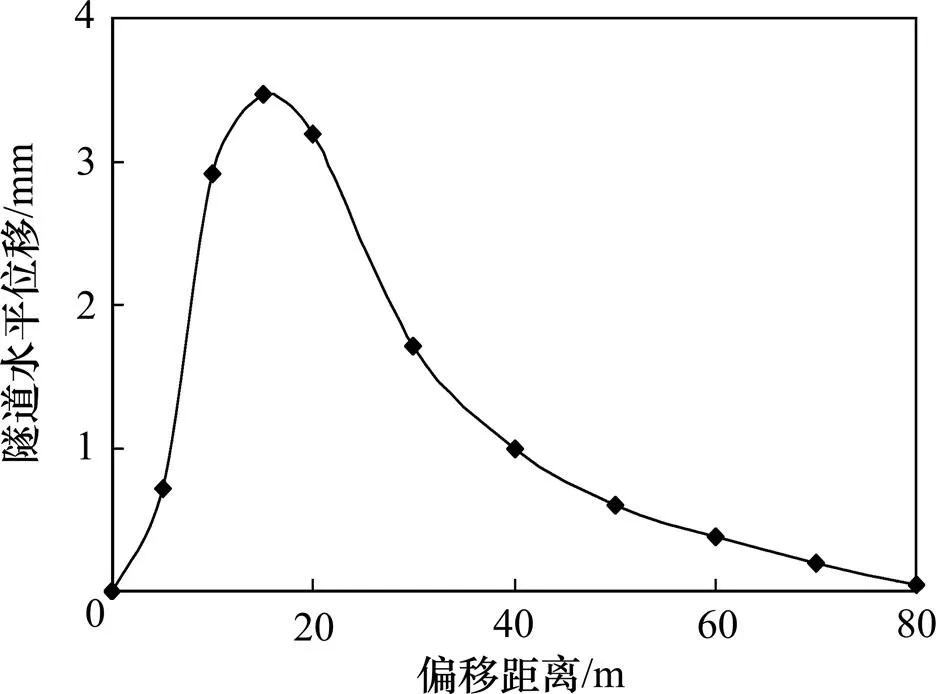
图9 y=0 m处盾构隧道水平位移变化曲线

图10 y=80 m处盾构隧道水平位移变化曲线

由图6和图8对比可知：地面堆载引起的隧道竖向位移要明显大于隧道水平位移，即竖向位移是控制指标，因此下面仅研究隧道竖向位移变化。

4.2 堆载面荷载q改变对隧道竖向变形的影响

在标准工况下以堆载面荷载作为控制变量，分别取为20，40，60，80，100和120 kPa这6种工况，研究改变对隧道竖向变形的影响规律。

图11所示为不同工况下计算得到的盾构隧道竖向位移曲线。从图11可知：随着逐渐变大，隧道沉降量也逐渐增加；当＞80 kPa时，隧道的最大竖向位移超过控制值20 mm[20]，隧道结构安全性下降，但隧道变形的影响范围并没有加大；隧道中间沉降变化较大，两端略有隆起但变化较小；本文结果与吴庆 等[11]的研究结论“堆载量越大，隧道变形越大，而且在堆载的正下方，隧道拱顶垂直附加位移达到最大值”相一致。

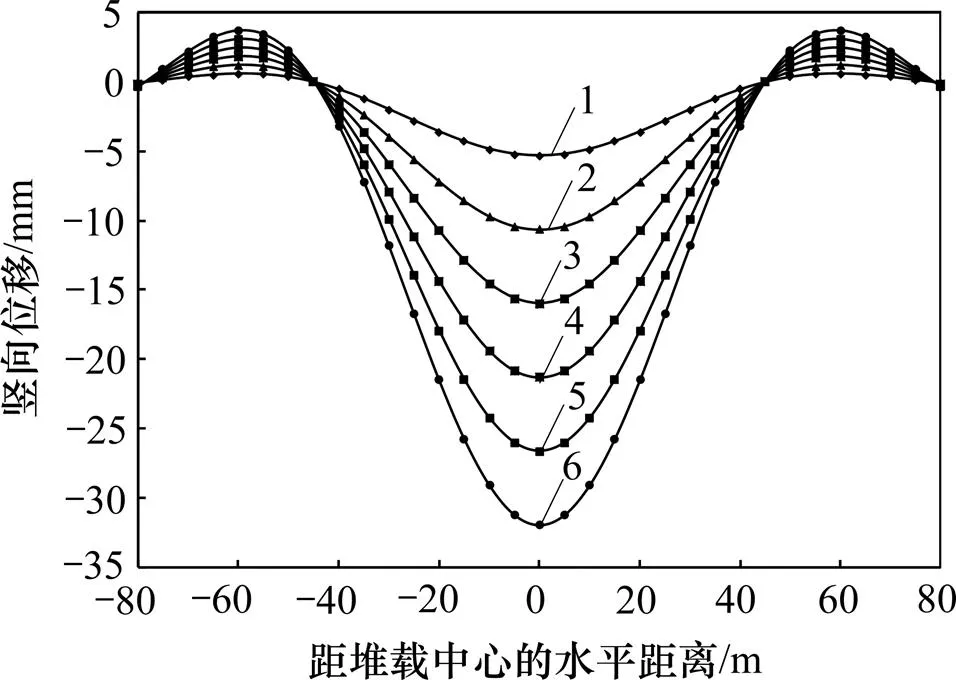
q/kPa：1—20；2—40；3—60；4—80；5—100；6—120。

图12所示为盾构隧道中心点(=0 m)处最大沉降随改变的变化曲线。从图12可知：隧道中心点的最大沉降随增大近似呈线性增加；当＞75 kPa时，隧道沉降量超过控制值20 mm[20]，因此，该工况下需要将控制在75 kPa以下，隧道结构才会安全。

图12 盾构隧道中心最大沉降量变化图

4.3 隧道覆土厚度h改变对隧道竖向变形的影响

在标准工况下仅改变隧道上方覆土厚度，不改变地面堆载数值和面积，分别取为9，14，19，24，29和34 m这6种工况，来研究改变对隧道竖向变形的影响规律。

图13所示为盾构隧道竖向位移随改变的变化曲线。从图13可知：随着增大，隧道整体沉降逐渐减小，最大值从26.6 mm降至11.9 mm，但沉降影响范围逐步扩大，从(−45，45) m扩展到(−70，70) m。表明埋深较大的隧道对地面堆载的抵抗能力强。

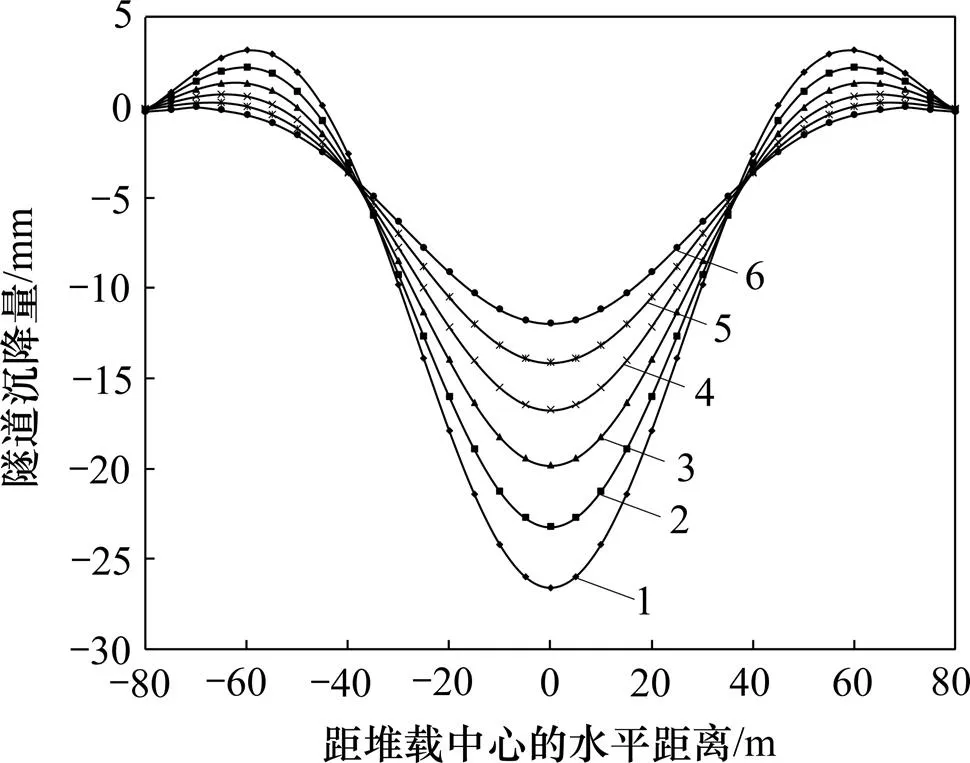
h/m：1—9；2—14；3—19；4—24；5—29；6—34。

4.4 堆载尺寸B和L改变对隧道竖向变形的影响

在标准工况下，分别改变地面堆载尺寸(垂直于隧道的堆载长度)和(沿隧道纵向或平行于隧道的堆载长度)，不改变堆载数值。

4.4.1改变对隧道竖向位移的影响

保持不变，分别取20，25，30，35和40 m这5种工况，研究改变对隧道变形的影响规律。图14所示为不同时计算得到的隧道竖向位移曲线。从图14可知：随着的增加，盾构隧道沉降曲线变化很小，最大沉降量略微增加、变化区间为(−26.62，−27.86) mm，同时，隧道的沉降影响范围也没有发生明显变化。表明与隧道垂直的地面堆载边长对隧道纵向位移的影响较小。

B/m：1—20；2—25；3—30；4—35；5—40。

4.4.2改变对隧道竖向位移的影响

保持不变，分别取20，25，30，35，40和45 m这6种工况，研究改变对隧道竖向变形的影响。图15所示为不同时计算得到的隧道竖向位移曲线。从图15可知：1)的取值范围在(20，35) m时，随着增大，隧道的沉降量和沉降影响范围都不断增大；2)的取值范围在(35，45) m时，随着增大，隧道的最大沉降值没有继续增大，但沉降影响范围进一步扩大。相比于，的改变对隧道位移产生的影响更加明显。所以，在实际工程中，当改变沿隧道纵向的地面堆载长度时，应加强对隧道的监测。

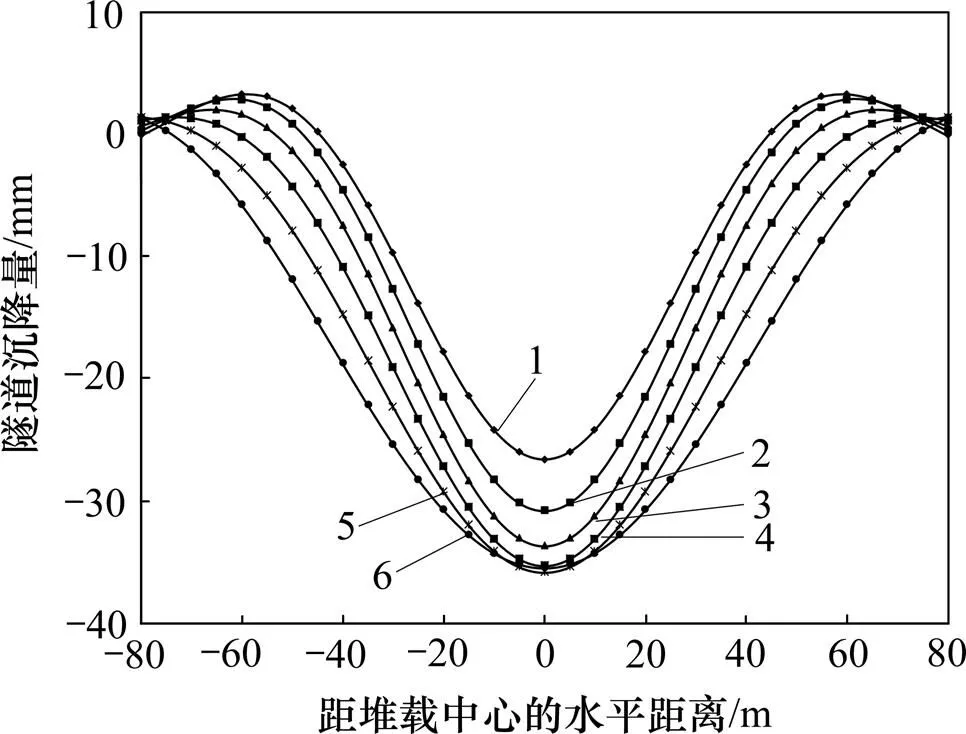
L/m：1—20；2—25；3—30；4—35；5—40；6—45。

5 结语

1) 本文方法能够计算得到由于地面堆载引起的盾构隧道纵向位移(包括竖向位移和水平位移)以及盾构隧道环之间的错台量和环间剪切力，由此可判断地面堆载作用下隧道结构的安全性。

2) 本文方法与有限差分法计算得到的盾构隧道沉降量在数值和趋势上都较为吻合；本文方法与弹性地基梁法对比，采用弹性地基梁法计算得到的隧道中部沉降量偏大。

3) 在上部地面堆载作用下，盾构隧道纵向变形大致呈正态分布，中间大、两端小，且影响范围较大；隧道主要产生竖向位移(尤其是沉降)，最大沉降量易超过控制值(20 mm)，其竖向位移要明显大于水平位移；管片的错台量和环间剪切力较小。

4) 随着增大，盾构隧道沉降量越来越小且减小速率加快，隧道的水平位移则呈先增大后减小趋势；越大，隧道的沉降量就越大，但隧道沉降影响范围并没有增大；随着增加，隧道最大沉降值减小，同时隧道沉降影响范围加大；的改变对隧道竖向位移影响非常小，的改变对隧道沉降量及范围的影响较大。

本文仅研究了盾构隧道和地面堆载相平行的工况，没有研究两者斜交的工况；对盾构隧道纵向变形的安全性评估偏简单，建议进一步研究盾构隧道横向变形(直径方向)；也可在隧道错台变形模型基础上，进一步考虑隧道的弯曲变形。

[1] 孙钧. 城市地下工程活动的环境土工学问题(下)[J]. 地下工程与隧道, 2000(1): 2−7. SUN Jun. Environmental geotechnical problems of urban underground engineering activities[J]. Underground Engineering and Tunnels, 2000(1): 2−7.

[2] 邵华, 黄宏伟, 张东明, 等. 突发堆载引起软土地铁盾构隧道大变形整治研究[J]. 岩土工程学报, 2016, 38(6): 1036−1043.SHAO Hua, HUANG Hongwei, ZHANG Dongming, et al. Case study on repair work for excessively deformed shield tunnel under accidental surface surcharge in soft clay[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(6): 1036−1043.

[3] Huang Hongwei, Zhang Dongming. Resilience analysis of shield tunnel lining under extreme surcharge: Characterization and field application[J]. Tunneling and Underground Space Technology, 2016, 51: 301−312.

[4] 徐志发, 王颖轶, 董越鹏, 等. 地面超载对大型盾构施工扰动位移的影响[J]. 交通建设与管理, 2010(5): 170−180. XU Zhifa, WANG Yingtie, DONG Yupeng, et al. Influence of ground overload on the displacement of large shield construction[J]. Traffic Construction and Management, 2010(5): 170−180.

[5] 王旭. 地面过量堆土对某地铁隧道的影响及结构安全分析[J]. 城市建设理论研究, 2013(12): 1−7. WANG Xu. Analysis of the influence of ground excess soil pile on a metro tunnel and its structural safety[J]. Theoretical Research on Urban Construction, 2013(12): 1−7.

[6] 李春良, 王国强, 赵凯军, 等. 地面荷载作用盾构隧道纵向力学行为[J]. 吉林大学学报(工学报), 2011, 41(增2): 180−184. LI Chunliang, WANG Guoqiang, ZHAO Kaijun, et al. Vertical mechanical behavior of shield tunnel under loads on ground surface[J]. Journal of Jilin University (Engineering and Technology Edition), 2011, 41(Supp.2): 180−184.

[7] 姜启元, 管攀峰, 叶蓉. 软土盾构隧道的纵向变形分析[J]. 地下工程与隧道, 1999(4): 2−6, 21. JIANG Qiyuan, GUAN Panfeng, YE Rong. Analysis of longitudinal deformation of shield tunnel in soft soil[J]. Underground Engineering and Tunnel, 1999(4): 2−6, 21.

[8] 侯芳. 均布荷载作用下温克勒弹性地基梁解析解及其在盾构隧道纵向计算中的应用[D]. 青岛: 青岛理工大学土木工程学院, 2009: 17−37. HOU Fang. Analytical solution of Winkler elastic foundation beam under uniform load and its application in longitudinal calculation of shield tunnel[D]. Qingdao: Qingdao Technological University. College of Civil Engineering, 2009: 17−37.

[9] 戴宏伟, 陈仁朋, 陈云敏. 地面新施工荷载对临近地铁隧道纵向变形的影响分析研究[J]. 岩土工程学报, 2006, 28(3): 313−317. DAI Hongwei, CHEN Renpeng, CHEN Yunming. Study on the influence of new construction loads on longitudinal deformation of adjacent metro tunnels[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(3): 313−317.

[10] 王如路, 张冬梅. 超载作用下软土盾构隧道横向变形机理及控制指标研究[J]. 岩土工程学报, 2013, 35(6): 1092−1101. WANG Rulu, ZHANG Dongmei. Mechanism of transverse deformation and assessment index for shield tunnels in soft clay under surface surcharge[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(6): 1092−1101.

[11] 吴庆, 杜守继. 地面堆载对既有盾构隧道结构影响的试验研究[J]. 地下空间与工程学报, 2014, 10(1): 57−66. WU Qing，DU Shouji. Model test on influence of ground heaped load on existing shield tunnel structure[J]. Journal of Underground Space and Engineering, 2014, 10(1): 57−66.

[12] 张明告, 周顺华, 黄大维, 等. 地表超载对地铁盾构隧道的影响分析[J]. 岩土力学, 2016, 37(8): 2271−2278. ZHANG Minggao, ZHOU Shunhua, HUAN Dawei, et al. Analysis of influence of surface surcharge on subway shield tunnel under[J]. Rock and Soil Mechanics, 2016, 37(8): 2271−2278.

[13] 王如路. 上海地铁盾构隧道纵向变形分析[J]. 地下工程与隧道, 2009(4): 1−6. WANG Rulu. Longitudinal deformation analysis for Shanghai subway tunnel constructed by shield method[J]. Underground Engineering and Tunnels, 2009(4): 1−6.

[14] 梁发云, 褚峰, 宋著, 等. 紧邻地铁枢纽深基坑变形特性离心模型试验研究[J]. 岩土力学, 2012, 33(3): 657−664. LIANG Fayun, CHU Feng, SONG Zhu, et al. Centrifugal model test research on deformation behaviors of deep foundation pit adjacent to metro stations[J]. Rock and Soil Mechanics, 2012, 33(3): 657−664.

[15] SHEN Shuilong, WU Huaina, CUI Yujun, et al. Long-term settlement behavior of metro tunnels in the soft deposits of Shanghai[J]. Tunnelling and Underground Space Technology, 2014, 40: 309−323.

[16] 刘晓强, 梁发云, 张浩, 等. 隧道穿越引起地下管线竖向位移的能量变分分析方法[J]. 岩土力学, 2014, 35(增刊2): 217−222, 231. LIU Xiaoqiang, LIANG Fayun, ZHANG Hao. Energy variational solution for settlement of buried pipeline induced by tunneling[J]. Rock and Soil Mechanics, 2014, 35(Supp. 2): 217−222, 231.

[17] VESIC A B. Bending of beams resting on isotropic elastic solids[J]. Journal of Engineering Mechanics, 1961, 87(2): 35−53.

[18] 周顺华, 何超, 肖军华. 环间错台效应下基坑开挖引起临近地铁盾构隧道变形的能量计算法[J]. 中国铁道科学, 2016, 37(2): 53−60.ZHOU Shunhua, HE Chao, Xiao Junhua. Energy method for calculating deformation of adjacent shield tunnels due to foundation pit excavation considering step between rings[J]. China Railway Science, 2016, 37(2): 53−60.

[19] 陈郁，李永盛. 基坑开挖卸载引起下卧隧道隆起的计算方法[J]. 地下空间与工程学报, 2005, 1(1): 91−94. CHEN Yu, LI Yongsheng. The calculation method of the uplift of the lower tunnel caused by excavation unloading[J]. Journal of Underground Space and Engineering, 2005, 1(1): 91−94.

[20] 上海市政法(94)第854号, 上海市地铁沿线建筑施工保护地铁技术管理暂行规定[S]. Shanghai Metro Line 854th(94), Interim provisions of Shanghai Municipality on the administration of the technical management of subway construction and protection[S].

[21] 林盼达, 张冬梅, 闫静雅. 运营盾构隧道结构安全评估方法研究[J]. 隧道建设, 2015, 35(增刊2): 43−49.LIN Panda, ZHANG Dongmei, YAN Jinya. Study on assessment method for structural safety of operating shield-bored tunnels[J]. Tunnel Construction, 2015, 35(Supp. 2): 43−49.

Study on calculation of shield tunnel shearing dislocation platform deformation due toadjacent ground stacked load

WEI Gang1, YU Guohua2, HONG Wenqiang3

(1. Department of Civil Engineering, Zhejiang University City College, Hangzhou 310015, China;2. Department of Civil Engineering and Architecture, Anhui University of Science and Technology, Huainan 232001, China;3. Institute of Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China)

The additional stress on the axis of shield tunnel was calculated by using the Boussinesq formula due to the adjacent ground stacked load. Then with the shearing dislocation platform model the vertical displacement, the dislocation of adjacent segments and the interannular shearing force of the subway shield tunnel in the sub-layer were calculated. In addition, an example analysis was made to study the influence on value of ground stacked load, the offset distance of the ground stacked load, the thickness of covering soil upon the shield tunneland the shield tunnel and the size of ground stacked loadand. The results show that the bigger the numerical value of stacked loadis, the bigger the settlement of the shield tunnel is, but the influence range of the shield tunnel’s settlement does not become bigger. The bigger the distance between the shield tunnel and the center of the ground stacked load is, the smaller the settlement of the shield tunnel is, and the shrinking speed of the settlement is bigger. As the offset distancebecomes bigger, the horizontal displacement of shield tunnel increases first and then shrinks. The thicker the covering soil is, the smaller the maximum settlement of the shield tunnel is, but the influence range of settlement of shield tunnel is bigger. The change of length of ground stacked load has a bigger influence on the settlement of the shield tunnel. The settlement of the shield tunnel is bigger than its horizontal displacement.

ground stacked load; shield tunnel; shearing dislocation platform; longitudinal displacement

10.11817/j.issn.1672-7207.2018.07.026

TU432

A

1672−7207(2018)07−1775−09

2017−07−02；

2017−10−28

国家自然科学基金资助项目(51778576)；杭州市科委资助项目(20180533B07) (Project(51778576) supported by the National Natural Science Foundation of China; Project(20180533B07) supported by the Technology Project of Hangzhou Municipal Science and Technology Commission)

魏纲，博士，教授，从事地下隧道与周边环境相互影响及风险评估与控制等研究；E-mail: weig@zucc.edu.cn

(编辑 杨幼平)