地铁用嵌入式轨道结构合理刚度研究

汪力，肖杰灵，王强，王平，刘光胜，罗信伟



地铁用嵌入式轨道结构合理刚度研究

汪力1, 2，肖杰灵1, 2，王强1, 2，王平1, 2，刘光胜3，罗信伟4

(1.高速铁路线路工程教育部重点实验室，四川 成都，610031；2. 西南交通大学 土木工程学院，四川 成都，610031；3.成都市新筑路桥机械股份有限公司，四川 新津，611430；4. 广州地铁设计研究院有限公司，广东 广州，510010)

针对嵌入式轨道应用于地铁环境时的刚度设计方法及合理取值开展研究。基于温克尔弹性地基梁理论，系统性地分析地铁用无扣件嵌入式轨道结构垂向、横向、抗倾覆、纵向及抗拔等各项刚度的组成及影响因素，并与传统扣件式轨道结构类比，形成各项刚度的设计、测试方法，给出取值建议。研究结果表明：嵌入式轨道垂、横向刚度可用钢轨基础弹性模量表征；纵向刚度与线路无缝化、限位结构以及高分子浇筑料施工锁定等有关；室内轨道结构样件测试验证了上述结果。建议：地铁用嵌入式轨道结构垂向钢轨单位长度基础弹性模量取32~64 kN/mm，横向钢轨单位长度基础弹性模量取24.76~91.57 kN/mm，一般地段纵向刚度不小于每轨15 kN/m，小阻力地段约每轨6.4 kN/m，抗拔力应不小于每轨32 kN/m。

地铁；嵌入式轨道；轨道刚度；连续支承

嵌入式轨道结构是设置有半包围的承轨槽，钢轨置于承轨槽内并被高分子材料、预制降噪块及橡胶垫板连续支承并约束的一种特殊轨道结构，该结构为钢轨提供了连续、均匀和可靠的空间约束，在钢轨减磨、减振降噪及日常养护维修等方面表现突出[1−2]。嵌入式轨道结构是随着现代有轨电车的兴起而发展起来的，荷兰、西班牙等正尝试将其应用于地铁甚至高铁和重载线路[3−4]。我国已在有轨电车线路应用了该种轨道结构，并开始探索将其作为一种具有优良减振降噪性能的新型轨道结构应用于地铁线路[5]。轨道是轮轨关系的固定部分和关键的承力和传力结构，需要一定的弹性缓解动力冲击，分散轮轨作用力，降低振动噪声，这一重要参数由轨道刚度表征[6−7]。轨道刚度作为结构的基本性能参数之一，是影响列车运行品质、轨道结构振动与变形以及路基、桥梁等下部结构动力响应的重要因素[8−11]。轨道结构存在且需要设计一个合理刚度[10−12]。关于轨道结构刚度合理值，国内外许多学者进行了大量的研究工作[8−16]。原铁道部也曾设立重大基础性研究专题“轨道结构刚度合理值及其合理匹配的研究”。赵国堂[12]提出了钢轨容许应力、轨道容许变形、临界速度等多种方法来确定轨道结构合理刚度及其部件刚度的匹配。刘学毅[13]应用轮轨系统动力学研究轨道刚度对轨道动力特性的影响规律，提出轨道动力参数对轨道刚度的敏感系数的概念，以此建立轨道总刚度取值、扣件与道床刚度比值的动力学优化分析方法。张格明[14]通过现场轨道结构刚度与部件刚度实测、轨道结构动力响应测试、室内轨道部件刚度测试、道砟动三轴试验数据及理论分析结果，建立了基于8个敏感参数和相应敏感系数的综合效应目标函数，来寻找轨道整体刚度和部件刚度的合理取值范围。蔡成标等[15]综合分析无砟轨道轨下基础刚度对轮轨动力学性能指标的影响规律，提出将刚度敏感参数进行“归一化”处理，以获得轨道结构合理刚度范围。其他相关研究见文献[16−18]。然而，嵌入式轨道结构因采用连续支承和约束，未设置扣件系统，其刚度设计与传统轨道结构有着较大差异。传统轨道结构的刚度设计，尤其是无砟轨道结构，主要通过扣件系统刚度来实现。缺少扣件系统的嵌入式轨道结构没有离散弹性支承部件，其垂、横、纵三向刚度及垂向抗拔力均需由约束钢轨的槽内结构提供，也是此类结构安全性、稳定性和减振降噪性能的重要保证。

1 嵌入式轨道结构的刚度组成

1.1 嵌入式轨道的主要结构特点

嵌入式轨道结构形式多样，主体结构一般采用预制或现浇混凝土轨道板，板上承轨台位置开有深槽，安置槽内结构，嵌入钢轨，只露出轨头和工作边。典型结构如图1所示[19]。

图1 嵌入式轨道结构典型构造示意图(葡萄牙里斯本地铁)

嵌入式轨道结构能够提供弹性的部分主要是承轨槽系统及板下垫层(隔离层)、限位结构等，且以承轨槽系统为主。承轨槽系统是嵌入式轨道结构的核心部分。为确保钢轨的可靠、稳定安装，承轨槽系统先施作钢轨、预制降噪块、调轨组件、弹性垫板等，再现浇高分子浇筑料，通过高分子材料的强力黏结最终形成一个牢固的整体结构。板下隔离层的设置可实现嵌入式轨道板的粗定位和维护，使轨道下部结构发生伤损、变形后，仍存在一定的修复能力。

1.2 嵌入式轨道结构刚度分析

地铁用嵌入式轨道结构承轨槽内一般包含钢轨、预制降噪块、轨底弹性垫板、调高垫板、调轨组件、高分子浇筑料等，如图2所示。为实现钢轨连续支承以及系统减振降噪需求，钢轨轨底设置连续弹性橡胶垫板，轨腰粘贴预制降噪块，并浇筑高分子材料锁固(图2)。

在承轨槽系统中，弹性垫板连续布置，与高分子浇筑料共同决定了系统垂向刚度。调高垫板间断按高程需求布置，空隙处由高分子浇筑料填充，且弹性模量与高分子浇筑料的相当以实现钢轨垂向连续均匀支承。

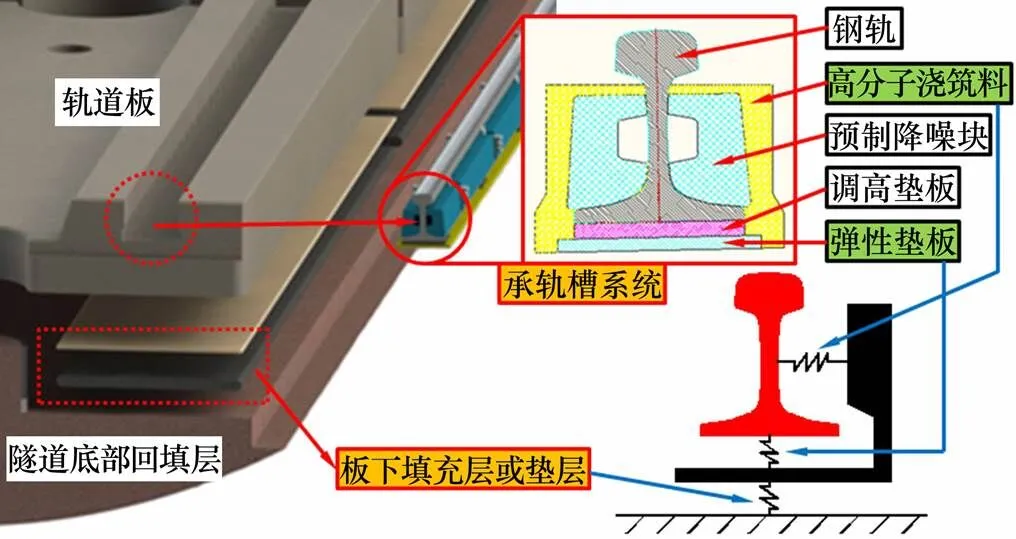
图2 地铁用嵌入式轨道结构刚度组成

预制降噪块按减振降噪需求设计形状、尺寸及材料参数。高分子浇筑料填充预制降噪块与钢轨、混凝土槽之间的空隙空间。两者共同决定承轨槽系统横向刚度。

预制降噪块与钢轨之间由强力胶黏接，高分子浇筑料与钢轨及混凝土槽壁均有一定黏接力。预制降噪块及高分子浇筑料的抗剪能力、轨底弹性垫板的摩擦阻力共同决定承轨槽系统的纵向阻力。

钢轨抗倾覆能力由槽内结构共同决定，轨底弹性垫板、预制降噪块及高分子浇筑料对钢轨抗倾覆能力均有一定影响[17]。

填充的高分子浇筑料与混凝土槽壁的黏结力以及混凝土槽的截面设计共同决定承轨槽系统的抗拔 水平。

由上述分析可知：嵌入式轨道结构的刚度虽主要由承轨槽系统决定，但由于承轨槽系统的复杂性，整个轨道结构的刚度组成也较复杂，各项刚度的影响因素均非单一因素，而是由至少2种材料共同决定。只有通过系统性地研究承轨槽系统的刚度，设置具有一定刚度和强度的槽内各种材料来有效约束钢轨，才能抵抗列车荷载、温度荷载等荷载的作用，保持轨道结构的空间几何形位，实现行车的安全性和稳定性。

2 各项刚度设计方法

2.1 垂向刚度

我国铁路垂向刚度研究中，常采用点支承梁模型和连续支承梁模型[6]，且两者之间有一定联系，如图3所示(图3中，为钢轨支座刚度，为钢轨基础弹性模量，为扣件间距)。嵌入式轨道结构因连续支承的结构特点，更适于采用连续支承梁模型进行垂向刚度分析。

连续支承梁模型用钢轨基础弹性模量表示基础的弹性特征，定义为使单位长度的钢轨基础产生单位下沉所需施加在其上的分布力。于是，无扣件连续支承嵌入式轨道结构的垂向刚度可用钢轨基础弹性模量来表征(不含钢轨抗弯刚度)。

我国地铁设计规范规定：无砟道床节点垂向静刚度(即钢轨支座刚度)为20~40 kN/mm，扣件间距为0.625 m[20]。由此，钢轨基础弹性模量建议范围：单位长度32~64 kN/mm。通过轨底弹性垫板及高分子浇筑料弹性模量的合理设置，以达到该钢轨基础弹性模量的建议范围。

综合考虑钢轨基础弹性模量与轨道结构整体刚度的关系[6]：

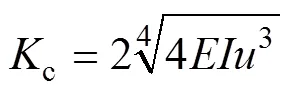
式中：c为轨道结构整体垂向刚度；为钢轨垂向抗弯刚度，中国标准60轨可取6.627×106N·m2；为钢轨基础弹性模量。

由式(1)可得轨道结构垂向整体刚度建议取值为61.06~102.69 kN/mm。

2.2 横向刚度及抗侧翻能力

钢轨的横向刚度和抗侧翻能力体现了系统对钢轨的横向约束及稳定性，主要可以通过控制轨头的横向位移及钢轨横截面的扭转(倾覆)角度实现(一般同时测定轨头和轨底位移来计算角度)，进而可以控制轨距的动态变化。

图3 轨道结构的两种垂向力学分析模型

嵌入式轨道结构横向刚度及钢轨抗侧翻能力主要由高分子浇筑料、预制降噪块及轨底弹性垫板共同决定。由于轮轨作用力位于轨头顶面及内侧，而嵌入式轨道的钢轨轨腰、轨底全部置于承轨槽内，被嵌入结构所包围，使得钢轨大部分处于路面以下，故其横向刚度及抗侧翻能力存在耦合，须一并考虑。

文献[21]对轨道结构几何动态平顺度控制有明确要求，对于时速低于100 km及介于100~120 km之间的线路，轨距动态不平顺允许值分别为(−5，+11) mm及(−5，+7) mm，轨距静态不平顺允许值为(−2，+3) mm。

基于温克尔弹性地基梁理论，轨道结构的整体横向刚度与钢轨最大横向动位移之间的关系可按下式考虑：

H=/动(2)

式中：为动力系数，1.5~2.0；为脱轨系数，限值0.8；为设计轮载；动为钢轨最大横向动位移，可按轨距动态不平顺允许值与静态不平顺允许值的差值的一半来考虑。

取动力系数为2.0，脱轨系数为0.8，设计轮载为80 kN，考虑到地铁线路设计时速一般低于100 km，则钢轨最大横向动位移(−1.5，4) mm，于是，地铁线路轨道结构整体横向刚度可取32~85.33 kN/mm。由式(2)确定轨道结构整体横向刚度。

再由式(1) (换成钢轨横向抗弯刚度，中国标准60轨可取1.079×106N·m2)、轨道结构整体刚度与钢轨基础弹性模量之间的关系，可确定横向钢轨单位长度基础弹性模量取值范围：24.76~91.57 kN/mm。

对于嵌入式轨道还应进一步考虑高分子浇筑料、预制降噪块与轨底弹性垫板三者自身的材料参数要求，以满足轨道结构安全性和平稳性的横向刚度需求。

2.3 纵向刚度

嵌入式轨道结构的纵向刚度主要考虑2方面：一是满足线路无缝化要求，主要包括桥上无缝线路的适应能力、断轨安全性和可施工性等，特别是桥上无缝线路铺设问题；二是满足轨道结构纵向限位的层间传力机制。

桥上无缝线路除有基本温度力外，还有伸缩力、挠曲力、制动力及断轨力等[22]。地铁用嵌入式轨道结构的梁轨相互作用研究可采用通用线—桥—墩一体化模型，借助有限元建模求解，但应结合结构样件纵向阻力测试曲线来设置线路的纵向刚度参数，如图4所示。

为便于维修、更换，适应桥梁变形，防止轨道结构错位或爬行，轨道板与下部结构之间须设置限位结构，如CRTSI型板式无砟轨道的轨道板与轨道板之间的圆柱凸台。限位结构约束了轨道板与板下结构之间的相对位移，形成了除承轨槽内高分子浇筑料及弹性垫板等约束钢轨纵向位移之外的第2层纵向约束层，整个轨道结构系统应满足层间纵向传力机制，如图5所示。

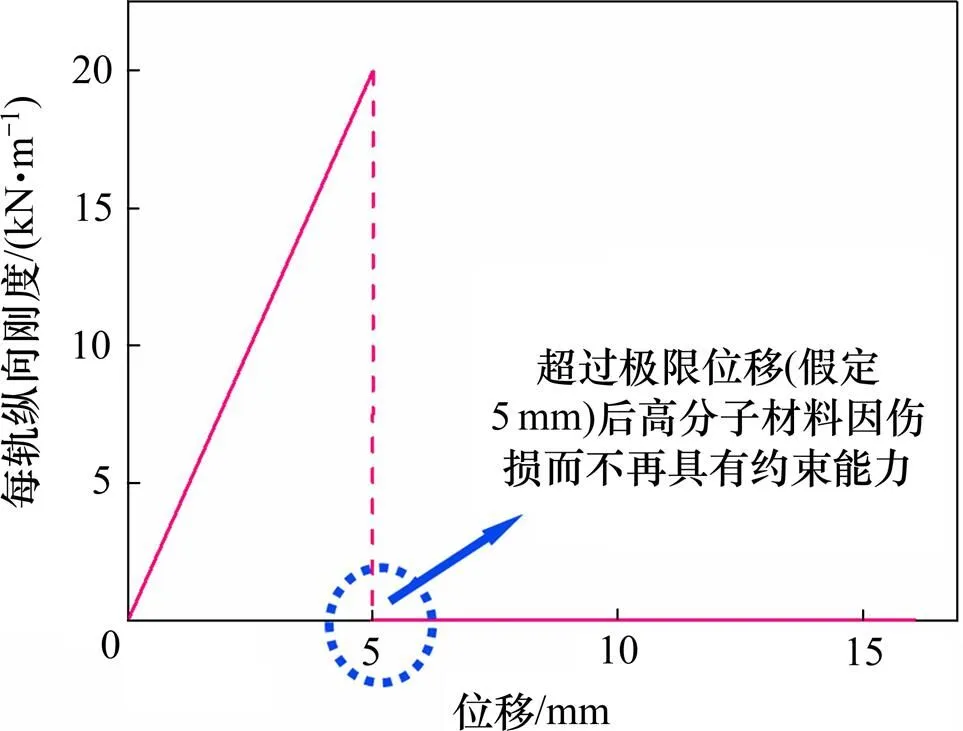
图4 嵌入式轨道纵向刚度参数示意图

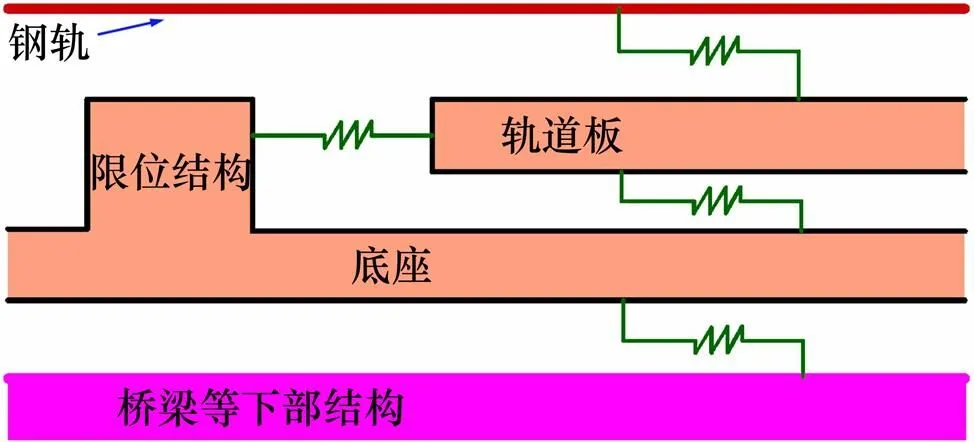
图5 轨道结构系统的层间纵向传力机制示意图

此外，嵌入式轨道结构在无缝线路施工锁定过程中还存在高分子材料无法瞬时凝固达到像扣件系统螺栓拧紧弹条扣压完毕即锁固钢轨的问题，故还需研究高分子材料刚度及强度随浇注时间的变化规律。结合不同凝固时间工况条件下的实测纵向阻力参数，对嵌入式轨道结构路基段无缝线路进行强度和稳定性分析，可提出嵌入式轨道无缝化施工的轨温变化限值。进而反向设计纵向阻力参数，对嵌入式轨道结构纵向刚度提出要求。

综合上述3方面的研究，地铁用嵌入式轨道结构的纵向刚度基本要求可建议设为：一般地段应大于每轨15 kN/m；小阻力地段约每轨6.4 kN/m。

2.4 抗拔能力

受凹竖曲线、桥梁端部位移、钢轨温升等作用，钢轨可能会受到上拔作用力，嵌入式轨道结构应考虑这一垂向抗拔刚度需求。

钢轨抗拔能力是与上拱失稳、线路平顺性保持等相关的一种约束机制，需进一步深入研究。若按竖曲线所用扣件系统扣压力一般取10 kN来粗略考虑，无扣件嵌入式轨道结构每轨抗拔力应不小于32 kN/m。

3 各项刚度的室内试验

3.1 样件的制备

为确认嵌入式轨道系统槽内结构能实现预期的各项刚度设计值，特试制了试验样件，以供测试。样件长×宽×高为600 mm×580 mm×250 mm，由混凝土槽、轨节、弹性垫板、预制降噪块及高分子浇筑料等组成，如图6所示。

图6 地铁用嵌入式轨道刚度测试样件

纵向及抗拔力测试样件轨条两端各超出混凝土槽约100 mm，即钢轨取800 mm长，以便于加载。

3.2 测试工装

针对嵌入式轨道样件测试，特设计图7所示的测试工装。

图8所示为使用该测试工装的室内地铁用嵌入式轨道样件刚度测试情况示例。

3.3 测试结果

由于钢轨长度较短，因此在垂向、横向刚度及抗拔力测试时，均不包含钢轨抗弯刚度的影响。垂向及横向刚度测试结果均为钢轨基础弹性模量。图9所示为样件垂向刚度测试所得典型测试结果。

图7 嵌入式轨道样件测试工装

(a) 垂向刚度测试；(b) 纵向刚度测试

表1所示为样件刚度测试情况。测试结果表明：由钢轨、轨下弹性垫板、降噪块、调轨组件和高分子浇筑料集成的槽内结构满足各项刚度目标要求。

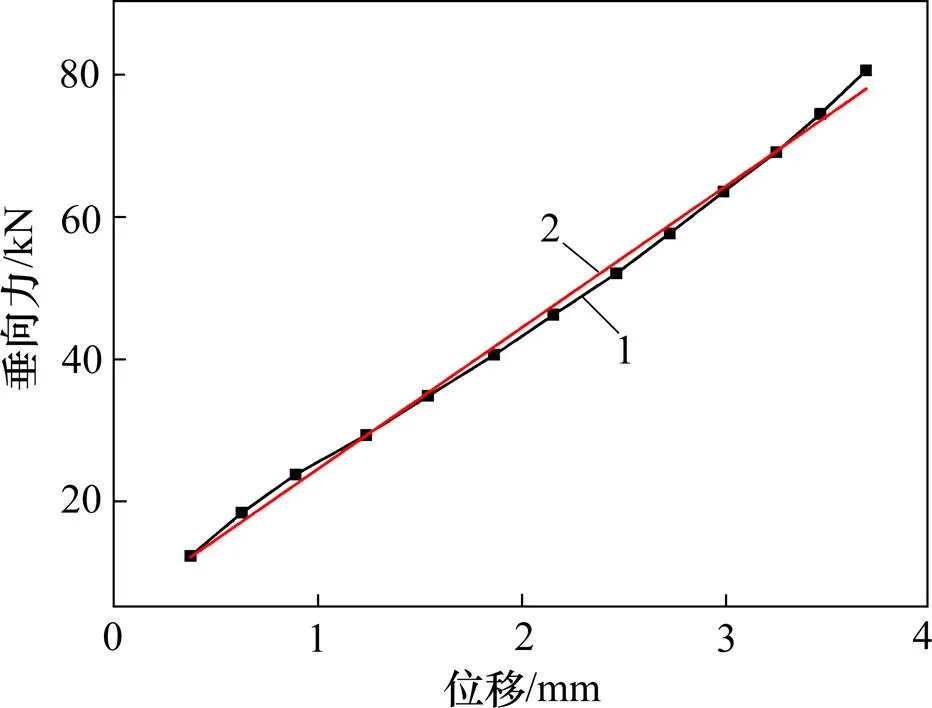
1—测试曲线；2—线性拟合。

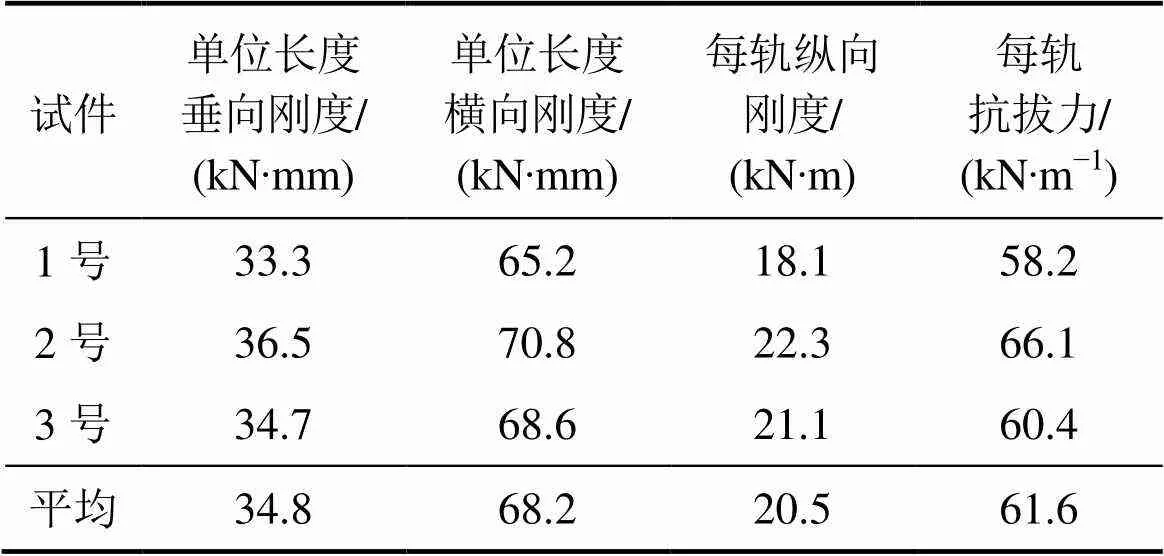
表1 样件刚度测试结果汇总

4 结论

1) 地铁用嵌入式轨道结构垂、横向刚度可参照扣件系统节点静刚度及几何动态平顺度控制的相关规定确定，建议垂向整体刚度取61.06~102.69 kN/mm；横向整体刚度取32~85.33 kN/mm。对应垂向钢轨单位长度基础弹性模量32~64 kN/mm；横向钢轨单位长度基础弹性模量24.76~91.57 kN/mm。

2) 嵌入式轨道纵向约束能力不仅要考虑无缝线路的梁轨相互作用，还应考虑限位结构以及高分子浇筑料熟化成型过程中的施工锁定问题，地铁用嵌入式轨道结构的纵向刚度基本要求建议：一般地段不小于每轨15 kN/m；小阻力地段约每轨6.4 kN/m。

3) 钢轨抗拔能力是与上拱失稳、线路平顺性保持等相关的一种约束机制，需进一步深入研究。

4) 嵌入式轨道结构样件测试表明，由钢轨、轨下弹性垫板、预制降噪块、调轨组件和高分子浇筑料集成的槽内结构满足各项刚度目标要求。

[1] ESVELD C. Modern railway track[M]. 2nd ed. Delft: Elsevier, 2001: 253−264.

[2] PERIARD F J. Wheel-rail noise generation: curve squealing by trams[D]. Delft: Delft University of Technology, 1998: 181−208.

[3] Edilon Sedra B V. Brochures from edilon)(sedra[EB/OL]. [2018−07−08]. https://www.edilonsedra.com/downloads/.

[4] PENNY C. Design and Manufacture of Embedded Rail Slab Track Components[R]. London: Balfour Beatty Rail Projects Ltd. 2008: 4−31.

[5] 汪力. 嵌入式轨道结构在地铁中的应用研究报告[R]. 成都: 西南交通大学高速铁路线路工程教育部重点实验室, 2016: 1−52. WANG Li. Report on the embedded track system used in metro[R]. Chengdu: Southwest Jiaotong University. Key Laboratory of High-speed Railway Engineering, Ministry of Education, 2016: 1−52.

[6] 李成辉. 轨道[M]. 成都: 西南交通大学出版社, 2005: 40−55. LI Chenghui. Railway track[M]. Chengdu: Southwest Jiaotong University Press, 2005: 40−55.

[7] WANG Ping, WANG Li, CHEN Rong, et al. Overview and outlook on railway track stiffness measurement[J]. Journal of Modern Transportation, 2016, 24(2): 89−102.

[8] SELIG E T, LI D. Track modulus: its meaning and factors influencing it[J]. Journal of the Transportation Research Board, 1994(1470): 47−54.

[9] FROHLING R D, SCHEFFEL H, EBERSOHN W. The vertical dynamic response of a rail vehicle caused by track stiffness variations along the track[J]. Vehicle System Dynamics, 1996, 25(1): 17−31.

[10] KERR A D. On the determination of the rail support modulus k[J]. International Journal of Solids and Structures, 2000, 37(32): 4335−4351.

[11] 翟婉明, 蔡成标, 王开云. 轨道刚度对列车走形性能的影响[J].铁道学报, 2000, 22(6): 80−83.ZHAI Wanming, CAI Chengbiao, WANG Kaiyun. Effect of track stiffness on train running behavior[J]. Journal of the China Railway Society, 2000, 22(6): 80−83.

[12] 赵国堂. 铁路轨道刚度的确定方法[J]. 中国铁道科学, 2005, 26(1): 1−6. ZHAO Guotang. Method for determining the rigidity of railway track[J]. China Railway Science, 2005, 26(1): 1−6.

[13] 刘学毅. 轨道刚度的影响分析及动力学优化[J]. 西南交通大学学报, 2004, 39(1): 1−5. LIU Xueyi. Effect analysis of track stiffness on dynamic characteristics of wheel-rail system and its dynamic optimization[J]. Journal of Southwest Jiaotong University, 2004, 39(1): 1−5.

[14] 张格明. 轨道刚度合理值评价指标的研究[J]. 中国铁道科学, 2002, 23(1): 51−57. ZHANG Geming. Research on right level of track structure stiffness and track-part stiffness[J]. China Railway Science, 2002, 23(1): 51−57.

[15] 蔡成标, 徐鹏. 高速铁路无砟轨道关键设计参数动力学研究[J]. 西南交通大学学报, 2010, 45(4): 493−497. CAI Chengbiao, XU Peng. Dynamic analysis of key design parameters for ballastless track of high-speed railway[J]. Journal of Southwest Jiaotong University, 2010, 45(4), 2010: 493−497.

[16] 王平, 徐金辉, 汪力, 等. 轨道刚度对车辆−轨道系统频率响应的影响[J]. 铁道工程学报, 2014, 31(9): 46−52. WANG Ping, XU Jinhui, WANG Li, et al. Effect of track stiffness on frequency response of vehicle-track coupling system[J]. Journal of Railway Engineering Society, 2014, 31(9): 46−52.

[17] 罗炯, 陈攀, 秦超红, 等. 有轨电车新型嵌入式轨道钢轨抗倾覆性能分析[J]. 铁道标准设计, 2016, 60(4): 8−12. LUO Jiong, CHEN Pan, QIN Chaohong, et al. Analysis of Rail Anti-turnover Performance for New Tramcar Embedded Track[J]. Railway Standard Design, 2016, 60(4): 8−12.

[18] 李现博. 现代有轨电车嵌入式轨道结构桥上梁轨相互作用研究[D]. 成都: 西南交通大学土木工程学院, 2015: 14−79. LI Xianbo. Research on interaction between girder and track on modern trams bridge with the structure of embedded track[D]. Chengdu: Southwest Jiaotong University. School of Civil Engineering, 2015: 14−79.

[19] CARELS P, VANDAMME L, PINTO P, et al. Continuously supported rail systems slab track system-experience of rossio tunnel brought to turkey[C]// International Symposium on Railway System Engineering (ISERSE’13). Karabük: Elsevier, 2013: 1−11.

[20] GB 50157—2013, 地铁设计规范[S]. GB 50157—2013, Code for design of metro[S].

[21] TB 10082—2005, 铁路轨道设计规范[S]. TB 10082—2005, Code for design of railway track[S].

[22] 广钟岩, 高慧安. 铁路无缝线路[M]. 4版. 北京: 中国铁道出版社, 2005: 223−306. GUANG Zhongyan, GAO Huian. Continuous welded rails[M]. 4th ed. Beijing: China Railway Publishing House, 2005: 223−306.

Reasonable track stiffness of embedded rail structure used in metro

WANG Li1, 2, XIAO Jieling1, 2, WANG Qiang1, 2, WANG Ping1, 2, LIU Guangsheng3, LUO Xinwei4

(1. Key Laboratory of High-speed Railway Engineering, Ministry of Education, Chengdu 610031, China;2. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China;3. Chengdu Xinzhu Road & Bridge Machinery Co. Ltd., Xinjin 611430, China;4. Guangzhou Metro Design & Research Institute Co. Ltd., Guangzhou 510010, China)

Design method and reasonable value of track stiffness are urgently needed when the embedded rail structure (ERS) was going to be applied in metro. Based on the theory of Winkler beam on elastic foundation, the configuration and influence factors of the stiffness of ERS, including vertical stiffness, horizontal stiffness, antidumping and vertical restraint were explored. Furthermore by analogy with the traditional tracks with fasteners, the design and measurement methods were formed and the reasonably suggested stiffness was presented. The results show that track modulus can be a better expressed with respect to ERS, in vertical or lateral direction. Track-bridge interaction and the strength of limited-location structure, as well as the rails’ anchoring considering the longitudinal restraint development in the process of polymer ripening should all be considered for the design of longitudinal constrain. The specimen test also verifies the conclusions above. It is suggested that the track modulus should be 32−64 kN/mm per meter in vertical direction and24.76−91.57 kN/mm per meter in transversal direction. The longitudinal restraint should be stronger than 15 kN/m per rail in normal sites and about 6.4 kN/m per rail on bridge where less restraint is needed. Vertical restraint should be no less than 32 kN/m per rail.

metro; embedded rail structure; track stiffness; continuous support

10.11817/j.issn.1672-7207.2018.07.033

U213.2

A

1672−7207(2018)07−1831−07

2017−07−05；

2017−09−19

国家杰出青年科学基金资助项目(51425804) (Project(51425804) supported by the National Science Fund for Distinguished Young Scholars)

肖杰灵，讲师，从事轨道结构及其动力学研究；E-mail: xjling@home.swjtu.edu.cn

(编辑 杨幼平)