结构参数和扰流参数对塔式太阳能接收器吸热管周向温差的影响

刘赟，李金芳，李永华



结构参数和扰流参数对塔式太阳能接收器吸热管周向温差的影响

刘赟，李金芳，李永华

(华北电力大学 能源动力和机械工程学院，河北 保定，071003)

通过改变吸热管的结构、在吸热管内插入扰流件的方法来减小塔式太阳能吸热管周向温差，提高接收器可靠性。与传统定温或定热流密度边界条件不同，采用HFCAL模型模拟实际非均匀太阳辐射分布，采用直圆管、渐缩管和渐扩管作为塔式太阳能接收器的吸热管结构，并进行对比分析。进一步分析不同扩张比渐缩管对周向温差的影响。研究结果表明：与光管和渐扩管相比，渐缩管聚光区与非聚光区的温差大幅度降低；周向温差随扩张比的增大而减小，当扩张比为20/16时效果较好，温差减小10%，压损为0.05 Pa；在渐缩管内插入扭曲片可进一步减小吸热管的周向温差，有效提高接收器可靠性。

塔式太阳能；接收器；周向温差；扭曲片

CSP(聚焦型太阳能)电站是太阳能发电的主要形式，包括塔式热发电、槽式热发电、碟式热发电和线性菲涅尔式热发电4种类型[1]。SPT(太阳能发电塔式发电技术)电站是所有CSP电站中效率较高、装机容量最大的，可使用各种不同的传热工质，因而具有很大的发展潜力[2]。在太阳能利用的研究领域中，提高光电/光热转化效率、降低成本、提高设备的可靠性具有深远意义。接收器是塔式太阳能热发电的核心传热设备，其性能直接影响整个电站的可靠性和光热转换效率。目前，管式接收器是塔式太阳能电站中最为常用的一种。然而，管式太阳能接收器普遍存在周向温差不均、热应力过大等问题，从而导致吸热管的变形或爆裂，影响接收器的安全运行[3]，因此，减小吸热管的周向温差是该类接收器的研究目标及紧要问题。邹琴梅[4]通过模型测得非均匀热流密度下塔式太阳能接收器吸热管的周向温差达83 K，会在吸热管上产生很大的热应力。DU等[5]分析了熔盐接收器吸热管上的热应力，其值远大于产生临界裂纹的热应力。因此，许多研究者希望通过降低周向温差的方法来提高接收器可靠性以及光热转化效率，其中包括调整定日镜场的布置、调整接收器布置位置、改变接收器材料、工质等方法。GARCIA-MARTIN等[6−8]通过调整定日镜场的布置使接收器得到更均匀的热分布。SALOME 等[9]测量接收器表面上不同点处的温度，当温度达到最大公差值时，通过改变定日镜的瞄准点将功率从一个区域传递到另一个区域从而调整吸热管表面的热流密度。BELHOMME等[10]采用蚁群元启发式优化目标点的程序，使定日镜场聚集的太阳能不集中辐照在1个点上，从而使接收器上能流密度分布均匀。除了调整定日镜场外，还可通过优化接收器的方式减小周向温差。LIAO等[11]对比分析不同工质下吸热管的传热效果从而选择合适的工质使吸热管的温差减小。VERLOTSKI等[12]通过实验验证了控制流体速率和保证吸热器效率的情况下逐渐增加射线辐照强度能减少热应力。BOEREMA等[13]模拟分析了4种吸热器(单一管径吸热器、多管径吸热器、多通道吸热器及理想流动吸热器)，模拟结果表明吸热管管道布置方式及采用不同位置、不同直径的吸热管能有效减少周向温差。LIAO等[14]在接收器入口端安装热管，使吸热管内的热量来自于热管的蒸发段而不是不均匀的太阳能辐射，从而消除温差。王婷等[15]结合气液两相传热和流动特点，将吸热管布置成两段式、多管程蛇形管布置方式，能较小部分热应力，AGRAFIOTIS等[16]为克服热应力及热冲击对吸热器造成的损害，选用了有良好抗热冲击的陶瓷材料，如再结晶SiC及硅元素渗入型SiC多孔蜂窝结构。FLORES等[17]提出并制造了Cu-Fe复合材质吸热器，能有效降低温度梯度，减小管内热应力。另一种方法是改变吸热管几何结构，即优化吸热管结构和在吸热管内插入扰流件。在结构优化方面，黄民等[18]分析渐扩管、渐缩管和直圆管内流体的流动特性，发现渐变管中流体的截面速度分布均匀，轴心速度下降，近壁处流体速度快，管内流体都能有效参与流动及换热。郝亚珍等[19]在微通道的热管理研究中使用了渐缩通道，发现来流在通道内的流速会更加均匀，各通道内反应物的浓度均匀，反应速率趋于一致。NAPHON等[20]将渐缩通道和螺旋通道等各通道类型进行对比，发现渐缩通道结构简单，易加工易获得，能有效改变流体的流动特性且压损较低。吸热管内插入扰流件也是改变吸热管流动特性的主要方式之一。MURUGESAN等[21]发现扭曲片扰流件对管内流体有分流与旋流作用，使管内流体边界层变薄，污垢沉积始终处在较低水平，增大流体的管内对流传热系数，从而到达强化传热的效果。塔式太阳能吸热管存在的周向温差问题十分显著，在此前的吸热管模型中基本采用定热流密度边界条件，从而导致模拟结果并不符合实际，因此，本文作者采用新的HFCAL变热流密度法来拟定吸热管的边界条件。渐缩管和渐扩管的多用于各工业管道的接口，其内工质的流动特性与直圆管的流动特性大不相同，而塔式太阳能接收器在此前鲜有采用渐缩管及渐扩管作为吸热管模型来提高可靠性的研究。本文选取渐缩管和渐扩管为吸热管，模拟分析其流动特性从而选取合适的吸热管模型。其后建立内置扰流件的吸热管模型，根据计算结果分析各模型对周向温差的影响，选取最佳的优化方案。

1 数学模型

1.1 工作原理

腔式管状太阳能接收器中，吸热管都布置在1个腔体中，太阳能通过1个透光窗口射入腔体，与接收器的工质在腔体内发生热交换，如图1所示[22]。该接收器的吸热管都布置在腔体内，使对流、辐射热损失减小，换热效率提高。太阳能辐射透过窗口，热流密度在吸热管束平面上呈不均匀分布，吸热管的聚光区和非聚光区会产生很大的温差。因此，采用改变吸热管结构和在吸热管内插入扭曲片扰流件的形式来改变流场，增强冷热流体的混合，使吸热管内的工质温度更加均匀。

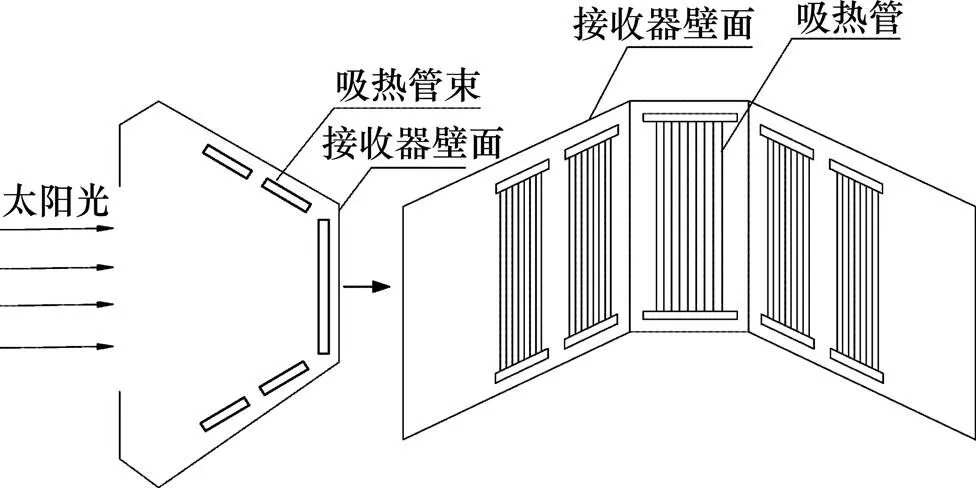
图1 腔式管状接收器[22]

1.2 控制方程

本文计算以三维笛卡儿坐标系为参照系，假定工质水蒸气为理想气体，工质的流动状态为定常流动，无内热源，流体计算域内的质量方程、动量方程、能量方程以及−方程如式(1)~(5)所示。

质量守恒方程：

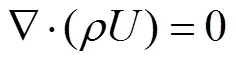
动量守恒方程：

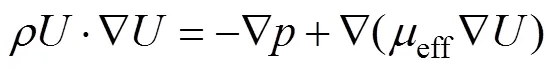
能量方程：

其中湍动能方程为

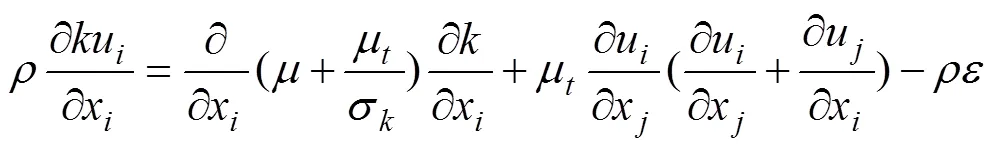
湍耗散方程为

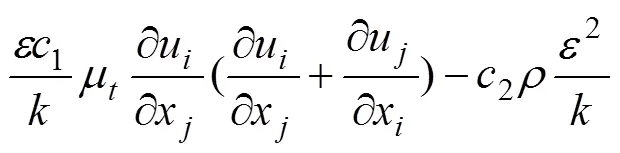
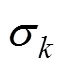
1.3 边界条件

本文采用HFUAL热流密度法，建立了与塔式太阳能电站定日镜场布置有关的模拟分析模型，其热流密度表达式[23]为

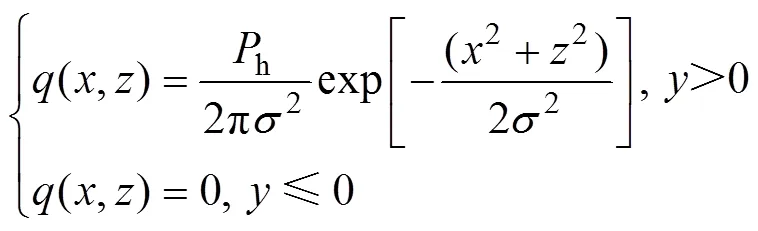
式中：为定日镜场中热辐射的有效偏差系数；Ph为单个定日镜发送的总功率，W；坐标x和z的原点对应于接收器平面上接收到的光辐射的中心点，其中x为接收器平面上沿管排方向上的坐标；z为接收器平面上沿管长方向上的坐标；y＞0表示聚光区，y≤0表示非聚光区。吸收管束平面上的热流密度分布如图2所示[24]，由原点向外热流密度逐渐减小。

2 物理模型

选取图2所示平面管束中位于管束中心的吸热管为研究对象，该吸热管的中心为吸热管束平面上光辐射的中心点，因此，可直接用式(6)进行热流密度的编程计算而不用换算坐标差值。图3所示为建立的直圆管、渐缩管和渐扩管三维立体模型。模型的尺寸参数为：直圆管长度为800 mm，直圆管横截面半径为 20 mm；渐缩管的长度为800 mm，渐缩管入口截面半径为20 mm，渐缩管出口截面半径为16mm；渐扩管长度为800 mm，渐扩管入口截面半径为16 mm，渐扩管出口截面半径为20 mm。

采用gambit建模，网格类型为Hex/wedge，网格密度为0.5。直圆管网格总数560万个，渐缩管网格总数为543万个，渐扩管网格总数为545万个。各模型网格=−0.4 m截面和=0 m截面网格分布如图4所示。

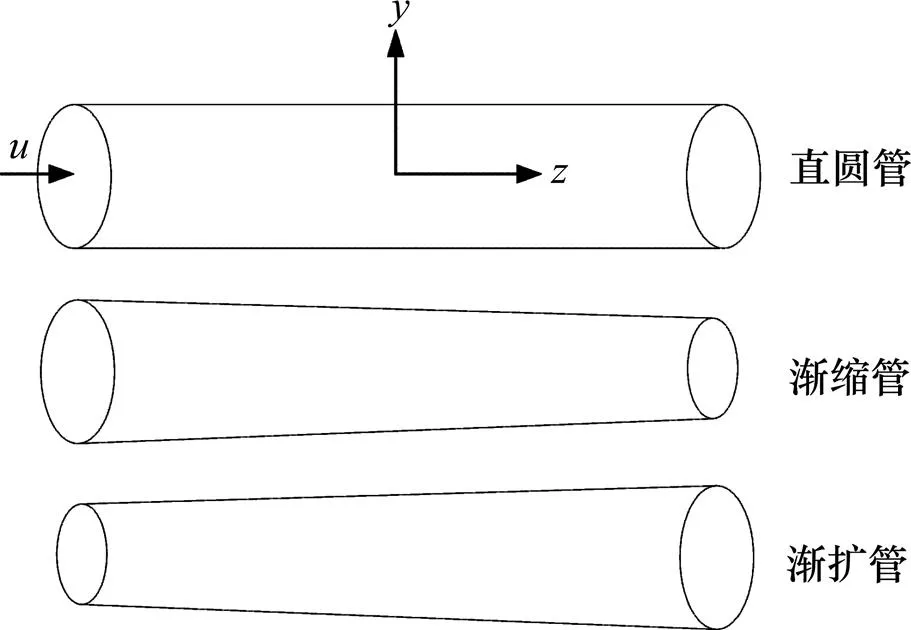
图3 不同热管结构模型图

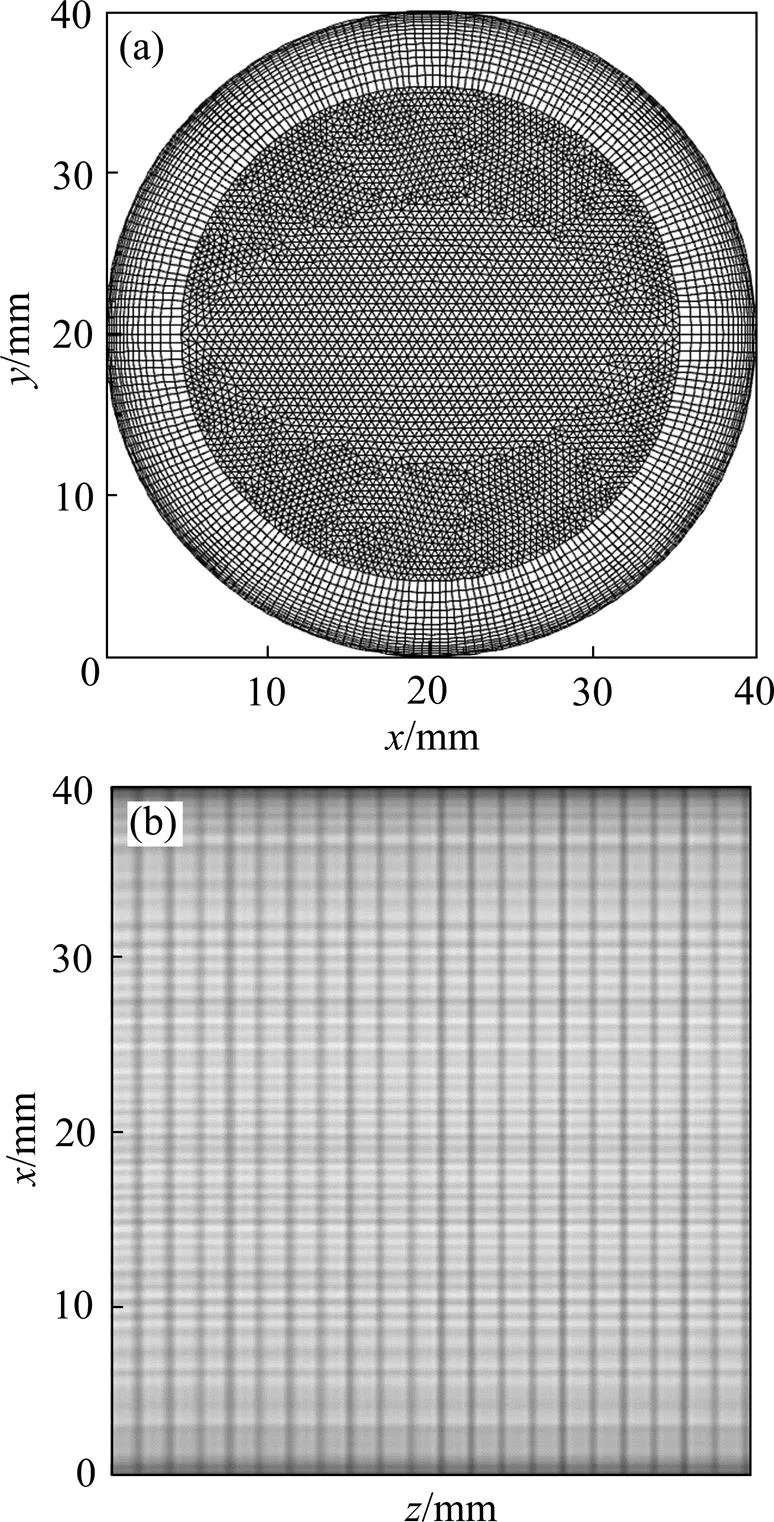
(a) z=−0.4 m截面网格；(b) y=0 m截面网格

扭曲片可在流场中产生纵向涡使流体产生扰动，从而使流体产生径向上的速度，加强冷热流体间的混合从而有效减小周向温差。在分析渐缩管的传热效果后，在渐缩管中加入扭曲片模型中渐缩管的长度为800 mm，入口截面半径为20 mm，出口截面半径为16 mm。扭曲片其底面长=8 mm，宽=3 mm，节距为400 mm。扭曲片数量为2片，均布置在渐缩管的非聚光侧，如图5(a)所示。由于扭曲片附近流体速度变化很大，为了提高计算结果的准确度，对扭曲片附近的网格进行加密。最靠近扭曲片的区域网格密度为0.5，所用的网格类型为Tet/hybird，该网格由四面体网格和楔形体网格混合而成。扭曲片往外部分的网格密度为0.7，所用的网格类型仍旧为Tet/hybird。吸热管近壁处网格密度为1.0，所用网格类型为Hex/wedge，该网格由四面体网格构成，在渐缩管壁贴壁处绘制边界层。=−0.4 m处的截面网格如图5(b)所示。

各模型的工质为水−水蒸气，在加热过程中吸热管内存在过冷段、湿蒸汽段及过热段。过热段内工质性质最为稳定，且水蒸气的传热性能不佳，过热段的周向温差会相对较大，因此，选择过热段为研究对 象。模型的入口工质温度为573.15 K，入口速度为 0.2 m/s。该过热蒸汽的物理参数为：=25.786 5 kg/m3，=2.069 5×10−5kg/(m∙s)，=0.056 8 W/(m∙K)，c= 3 207 J/(kg∙K)。

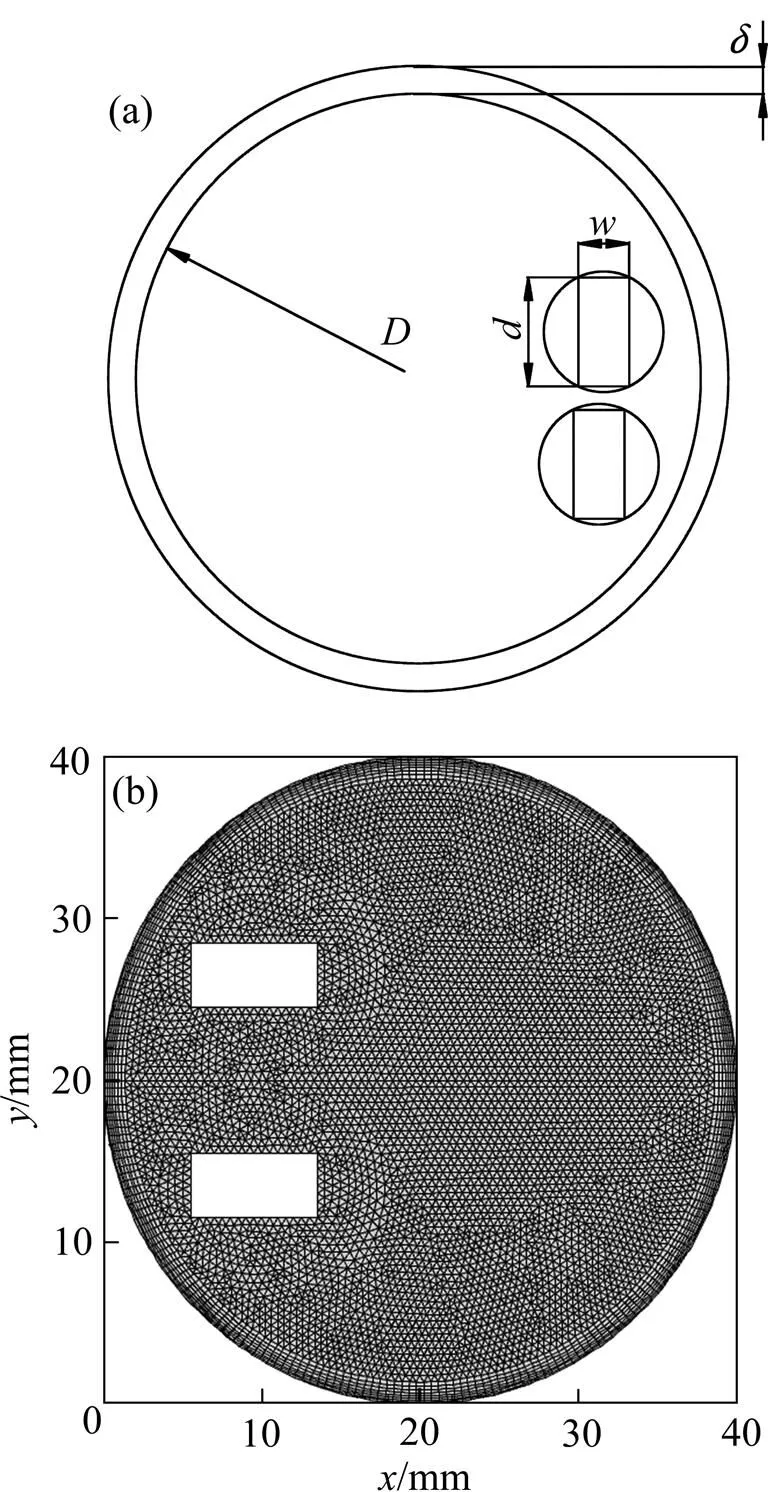
(a) 扭曲片布置图；(b) z=−0.4 m截面网格

网格的数量决定了计算的准度。为了保证计算结果的准确性，对3个模型的网格进行网格无关性验证。绘制模型的网格数为5 926×785，6 017×806， 6 154×845，6 154×909和6 243×945个共5种，这几个网格数量下吸热管的出口温差分别为36.0，37.1，38.5，39.0，39.1 K，如图6所示。计算发现网格数量为6 154×909个和6 243×945个时，出口温差的改变量仅为0.25%，所以，选取网格数为6 154×909个时的网格为计算网格。

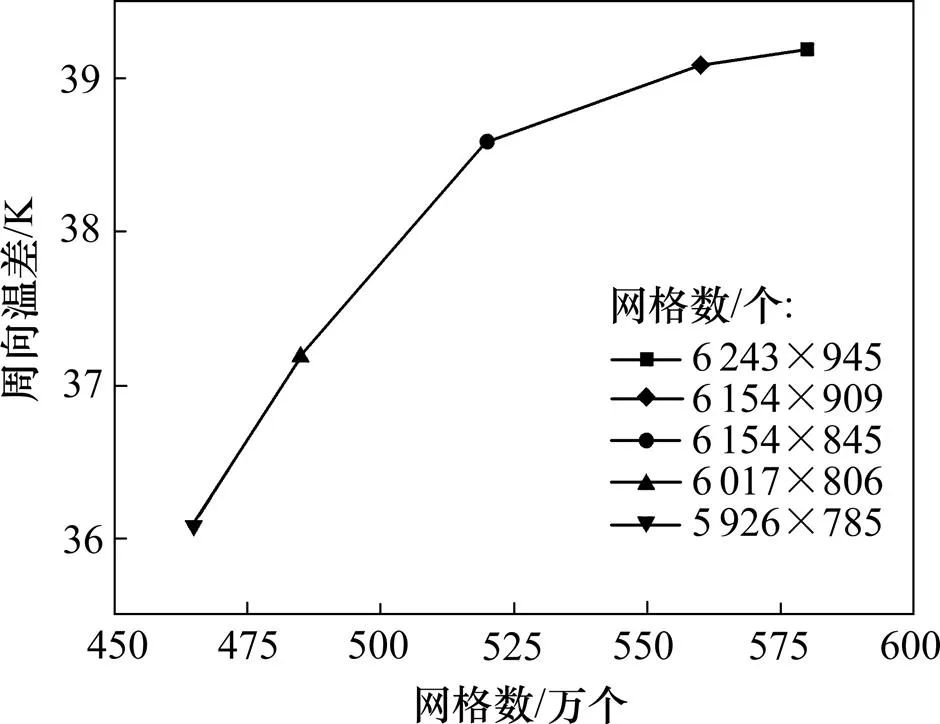
图6 网格无关性验证

3 结果与讨论

3.1 不同吸热管结构对出口温差的影响

图7所示为直圆管，渐缩管和渐扩管出口截面上的温度云图。由图7可以看出：直圆管出口截面周向温差最大为60 K；渐缩管出口截面周向温差减小为41 K，与直圆管相比减小了约33%；渐扩管出口截面上的周向温差和直圆管的相差很小，温差仍旧为 60 K。直圆管中的流体在管内流动时边界层较厚，沿管子径向上存在明显的速度梯度，贴近管壁处流速低，流动中心流速高，导致贴壁处的流体曝光时间长温度高，管道中心的流体温度相对较低，非聚光区的流体温度相对更低，吸热管聚光区和非聚光区产生较大的温差。渐缩管使得流体在管道中心的速度低，近壁处流速沿流动方向逐渐增大，从而径向的速度梯度较小，近壁处和中心处的速度相差不大。近壁处的流体与流动中心的流体不会因流速不同产生温差，从而使吸热管的周向温差减小。而渐扩管中流体的流速在径向上分布均匀，但是在纵向上流速减慢，流体在管内总停留时间增大，流体的温升较大，温差并没有减小。对不同吸热管结构进行研究的目的是为了减少吸热管的周向温差，因此，通过对比，本文选择渐缩管来取代直圆管成为接收器的吸热管。

3.2 渐缩管的扩张比对出口温差的影响

渐缩管相较于直圆管而言其管内工质的周向温差较小，而渐缩管中影响周向温差的主要因素为渐缩管的扩张比(=max/min，即渐缩管最大截面直径max与最小截面直径min的比值)。建立长度为800 mm、入口截面半径都为20 mm、出口截面直径分别为18，16和14 mm的3个渐缩管模型，网格画法与第2小节中的相同。图8所示为不同扩张比渐缩管的出口温度云图。由图8可知：渐缩管的扩张比越大，渐缩管的周向温差越小；当扩张比=20/18时，周向温差为45 K；当扩张比=20/16时，周向温差减小为41 K；当扩张比为=20/14时，周向温差减小到37 K。当渐缩管的扩张比越大时，近壁处流体的流速与中心流体的流速相差越小，管子内流体的混合更加均匀，从而减小温差。渐缩管的扩张比并不是越大越好。因为渐缩管的扩张比受渐缩管自身性能的影响，渐缩管的出口截面直径不能小于渐缩管的临界直径；此外，渐缩管的扩张比越大，其产生的压损就越大，需要消耗更多的泵功，降低了系统的经济性。图9所示为以渐缩管的出口截面直径为横坐标，左侧的纵坐标表示吸热管的出口截面上的周向温差，右侧的纵坐标表示吸热管的压损。由图9可知：当=20/18时，吸热管压损为0.03 Pa；当=20/16时，压损增大了67%；当=20/14时，压损增大到0.17 Pa。当渐缩管出口管径不断减小时，减缩管压损增加的速率高于渐缩管周向温差减小的速率，可见渐缩管的缩放比并不是越小越好。当渐缩管的扩张比=20/16时压损曲线与温差曲线相交，达到温差和压损综合考虑的最优点。

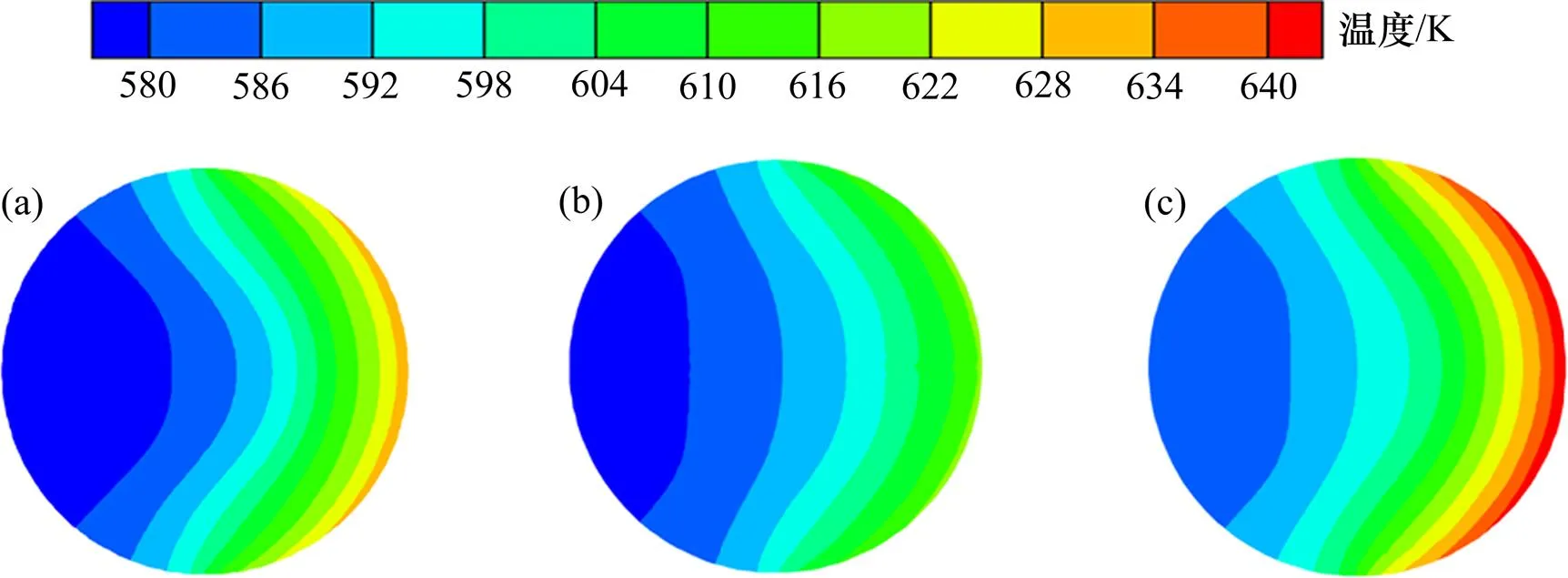
(a) 直圆管；(b) 渐缩管；(c) 渐扩管

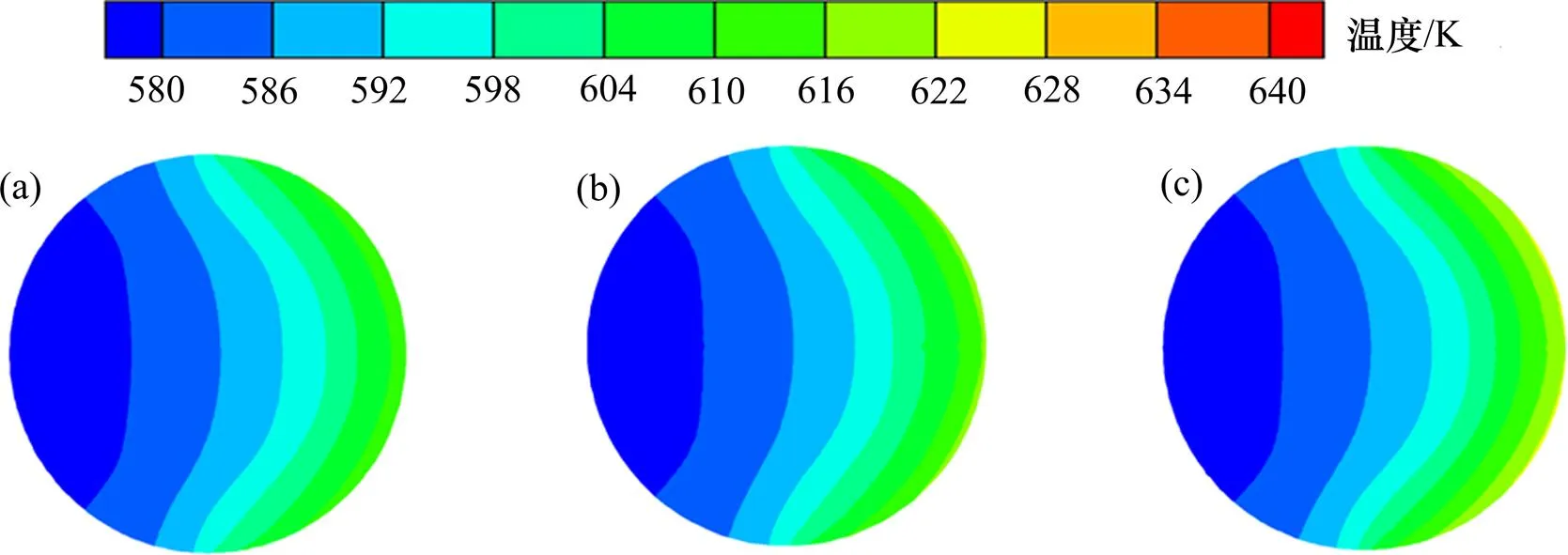
扩张比a：(a) 20/14；(b) 20/16；(c) 20/18

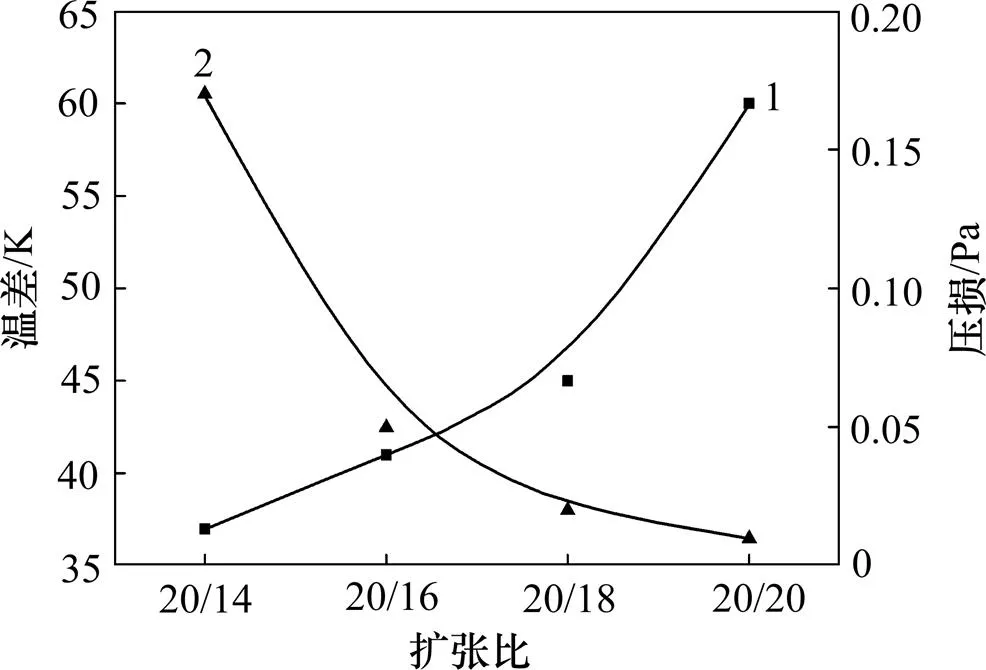
1—温差；2—压损。

3.3 渐缩管内插入扭曲片对温差的影响

图10所示为单直圆管，单渐缩管和内置扭曲片的渐缩管的出口截面的温度云图。从图10可见：直圆管的出口截面周向温差最大为60 K；渐缩管的周向温差为41 K；在渐缩管内置入扭曲片后温差进一步减小，内置扭曲片的渐缩管出口截面的温差缩小到只有 32 K。使用渐缩管使管内径向上速度分布均匀，减小温差；而在管内插入扭曲片能进一步对工质进行扰动，管内流体收到扭曲片的阻碍、分流而产生二次流，增强了径向旋流，加强了上下半周流体的混合，减小了径向温度场变化梯度，最终导致管内膜传热系数增大，从而达到强化传热和减小温差的效果。内置扭曲片的渐缩管出口截面速度矢量图如图11所示。从图11可见：扭曲片横截面速度矢量可达0.015 m/s，内置扭曲片会使流体产生纵向涡，使高温流体扰动到低温流体区域，加强了冷热流体混合从而使温差减小。渐缩管内的流体流速均匀，径向上速度梯度小，扭曲片在渐缩管内能充分带动管内的流体进行混合换热，使流体出口温差再度减小。在考虑优化温差的同时还是要考虑压损，图12所示的曲线图横坐标为吸热管类型，左边的纵坐标表示周向温差，右边的纵坐标表示压损。通过分析可发现在渐缩管内插入扭曲片后压损增大至0.08 Pa，与单渐缩管相比压损增大了60%。压损线与温差线的交点在单渐缩管附近，说明内置扭曲片的渐缩管虽能有效减小温差，但是压损增大会使经济性降低。在渐缩管内置入扭曲片虽然会增大压损，但是压损增大的幅度较小仅为0.03 Pa，而且在温差减小的情况下提高了吸热管的出口平均温度，仍存在一定的实用性，因此，可根据各接收器及电站的要求选取合适的优化方案。

(a) 直圆管；(b) 渐缩管；(c) 带扭曲片渐缩管

图11 内置扭曲片渐缩管出口截面速度矢量图

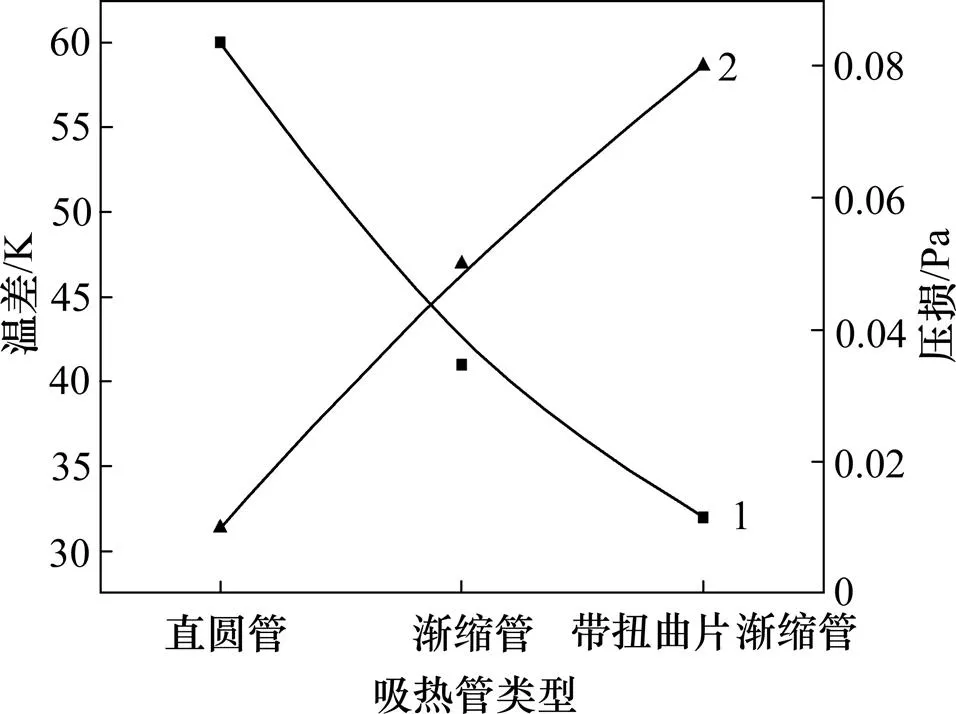
1—温差；2—压损。

4 结论

1) 渐缩管和渐扩管在工业中应用广泛，但是非均匀热流条件下的塔式接收器中应用较少。流体流经渐缩管后速度升高、压力降低，管内流体中心处到贴壁处的速度梯度减小，渐缩管内边界层的厚度与直圆管相比大大削薄，流体的温度较为均匀，能有效减小吸热管的周向温差。流体流经渐扩管后流速降低，压力升高，由于流速的减小使流体在管内的停留时间增大，因此，渐扩管出口的流体温度升高，对温差的影响 不大。

2) 渐缩管的扩张比是对吸热管内流体出口温差影响较大的结构参数。扩张比越大，吸热管的出口温差越小，但是造成的压损会越大，对不同扩张比下吸入管内流体的出口温差和吸热管两端的压损进行分析，可得当扩张比为20/16时性能最优。

3) 在渐缩吸热管内置入扭曲片扰流件能进一步减小吸热管的周向温差，提高出口平均温度。扭曲片产生的纵向涡能有效卷吸四周的流体，使冷热流体有效混合，进一步减小温差，但是会使压损略有增大，应综合实际情况选择最佳的优化方案。

[1] ROMERO M, BUCK R, PACHECO J E. An update on solar central receiver systems, projects and technologies[J]. Journal of Solar Energy Engineering, 2002, 124: 98−108.

[2] BAHAROON D A, RAHMAN H A, OMAR W Z W, et al. Historical development of concentrating solar power technologies to generate clean electricity efficiently: a review[J]. Renewable and Sustainable Energy Reviews, 2015, 41: 996−1027.

[3] 崔文智, 李洪香. 非均匀热流密度下太阳能吸热管的温度特性[J]. 电源技术, 2015, 39(5): 1040−1042. CUI Wenzhi, LI Hongxiang. Temperature characteristics of solar heat absorber tubes with non-uniform heat flux[J]. Power Technology, 2015, 39(5): 1040−1042.

[4] 邹琴梅. 塔式太阳能熔盐吸热器的传热特性研究与设计[D]. 杭州: 浙江大学控制科学与工程学系, 2014: 1−61. ZOU Qinmei. Stufy of flow and heat transfer performance and design of molten receiver in solar power plants[D]. Hangzhou: Zhejiang University. Department of Control Science and Engineering, 2014: 1−61.

[5] DU Baocun, HE Yaling, ZHENG Zhangjing, et al. Analysis of thermal stress and fatigue fracture for the solar tower molten salt receiver[J]. Applied Thermal Engineering, 2016, 99: 741−750.

[6] GARCÍA-MARTÍN F J, BERENGUEL M, VALVERDE A, et al. Heuristic knowledge-based heliostat field control for the optimization of the temperature distribution in a volumetric receiver[J]. Solar Energy, 1999, 66(5): 355−369.

[7] HAMZA K, GANDHI U, SAITOU K. Optimal scheduling of parabolic heliostats aim targets in a mini-tower solar concentrator system[C]// ASME 2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Washington, DC, USA, 2011: 351−358.

[8] VANTHULL L L, IZYGON M E, PITMAN C L. Real-time computation and control of solar flux density on a central receiver (Solar Two) (Preheat)[C]// American Society of Mechanical Engineers International Solar Energy Conference. San Antonio, TX, USA, 1996: 139−142.

[9] SALOMÉ A, CHHEL F, FLAMANT G, et al. Control of the flux distribution on a solar tower receiver using an optimized aiming point strategy: Application to THEMIS solar tower[J]. Solar Energy, 2013, 94(4): 352−366.

[10] BELHOMME B, PITZ-PAAL R, SCHWARZBÖZL P. Optimization of heliostat aim point selection for central receiver systems based on the ant colony optimization metaheuristic[J]. Journal of Solar Energy Engineering, 2014, 136(1): 190−198.

[11] LIAO Zhirong, LI Xin, XU Chao, et al. Allowable flux density on a solar central receiver[J]. Renewable Energy, 2014, 62(3): 747−753.

[12] VERLOTSKI V, SCHAUS M, POHL M. A solar thermal MgO-powder receiver with working temperatures of more than 1 600℃: model investigation by using a laser as an irradiation source[J]. Solar Energy Materials & Solar Cells, 1997, 45(3):227-239.

[13] BOEREMA N, MORRISON G, TAYLOR R, et al. High temperature solar thermal central-receiver billboard design[J]. Solar Energy, 2013, 97: 356−368.

[14] LIAO Z, FAGHRI A. Thermal analysis of a heat pipe solar central receiver for concentrated solar power tower[J]. Applied Thermal Engineering, 2016, 102: 952−960.

[15] 王婷, 庞力平, 杨勇平. 两段式塔式太阳能腔式吸热器设计及性能分析[J]. 动力工程学报, 2017, 37(4): 313−320.

WANG Ting, PANG Liping, YANG Yongping. Design and performance analysis of a two-stage tower-type solar cavity receiver[J]. Journal of Chinese Society of Power Engineering, 2017, 37(4): 313−320.

[16] AGRAFIOTIS C C, MAVROIDIS I, KONSTANDOPOULOS A G, et al. Evaluation of porous silicon carbide monolithic honeycombs as volumetric receivers/collectors of concentrated solar radiation[J]. Solar Energy Materials & Solar Cells, 2007, 91(6): 474−488.

[17] FLORES V, ALMANZA R. Behavior of the compound wall copper–steel receiver with stratified two-phase flow regimen in transient states when solar irradiance is arriving on one side of receiver[J]. Solar Energy, 2004, 76(1): 195−198.

[18] 黄民, 匡震邦. 渐缩(扩)直圆管中的发展流动[C]// 中国工程热物理学会热机气动热力学学术会议. 湖北宜昌, 1995: 74−81. HUANG Min, KUANG Zhenbang. Developing flow in a converging tube and a diverging tube[C]// Chinese Society of Engineering Thermophysics. Yichang, Hubei, 1995: 74−81.

[19] 郝亚珍. 微通道甲醇重整制氢过程的热管理研究[D]. 北京: 华北电力大学能源动力与机械工程学院, 2011: 1−42. HAO Yazhen. Study on thermal management of hydrogen production from micro-channel methanol reforming[D]. Beijing: North China Electric Power University. School of Energy Power and Mechanical Engineering, 2011: 1−42.

[20] NAPHON P, SOOKKASEM A. Investigation on heat transfer characteristics of tapered cylinder pin fin heat sinks[J]. Energy Conversion & Management, 2007, 48(10): 2671−2679.

[21] MURUGESAN P, MAYILSAMY K, SURESH S, et al. Heat transfer and pressure drop characteristics in a circular tube fitted with and without twisted tape insert[J]. International Communications in Heat and Mass Transfer, 2011, 38(3): 329−334.

[22] WEI Han, JIN Hongguang, SU Jianfeng, et al. Design of the first Chinese 1 MW solar-power tower demonstration plant[J]. International Journal of Green Energy, 2009, 6(5): 414−425.

[23] COLLADO F J. One-point fitting of the flux density produced by a heliostat[J]. Solar Energy, 2010, 84(4): 673−684.

[24] HAO Yun, WANG Yueshe, HU Tian. The flow distribution in the parallel tubes of the cavity receiver under variable heat flux[J]. Applied Thermal Engineering, 2016, 108: 641−649.

Effects of structural and disturbing flow parameters on circumferential temperature difference in tower solar receiver

LIU Yun, LI Jinfang, LI Yonghua

(School of Energy, Power and Mechanical Engineering, North China Electric Power University, Baoding 071003, China)

In order to improve the reliability of solar tower receiver, the different absorber structures and the twisted-tape insert were developed to homogenize the circumferential temperature distribution. Different from the traditional given temperature and heat flux boundary condition, in this contribution, the HFCAL model was applied to simulate the actual non-uniform solar flux distribution on the receiver tubes, and the cylinder pipe, tapered conduit and diffuser tube were used as absorbers to analyze the convective flow and heat transfer. Based on those models, the effects of expansion ratio of the tapered conduit were analyzed. The results show that the circumferential temperature difference of the tapered conduit is the smallest. The circumferential temperature difference decreases with the increase of the expansion ratio. The excellent effect can be obtained when the expansion ratio is 20/16, and the temperature difference reduces by 10%, and the pressure loss is only 0.05 Pa. Finally, adding the twisted-tapes to the tapered conduit can further reduce the circumferential temperature difference and improve the reliability of receiver.

tower type solar power; receiver; circumferential temperature difference; twisted-tapes

10.11817/j.issn.1672-7207.2018.07.032

TK514

A

1672−7207(2018)07−1823−08

2017−07−17；

2017−09−23

国家自然科学基金资助项目(51706072)；中央高校基本科研业务费面上资助项目(2015MS120) (Project(51706072) supported by the National Natural Science Foundation of China; Project(2015MS120) supported by the Fundamental Research Funds for the Central Universities of China)

刘赟，博士，讲师，从事新能源热利用领域的工程热物理问题研究；E-mail: liuyunlucia@ncepu.edu.cn

(编辑 杨幼平)