改进型Mertz法在多光谱数据重建中的应用*

李娟，孙秀玲，孙海峰

(长春理工大学光电信息学院，吉林 长春 130000)

光谱检测在航空航天、医药、科研等领域[1]都有广泛的应用。随着其技术的不断发展，对光谱数据处理的要求也日新月异。多光谱数据分析因能够同时完成对不同波长光谱的反演，一直是研究的热点，例如：多光谱的高速采集与处理、多光谱标定与重建等[2-5]。其中，存在多个特征峰值时如何准确地判断其波长及振幅是光谱测试的重点。

依据其工作原理，光谱探测主要分为光栅型和干涉型[6]。光栅型精度高，分光特性好，但狭缝结构的存在必然影响系统的光通量，使其在微弱光信号测试中难以应用[7-8]。干涉型主要是通过相干作用分析光谱分布，分时间型和空间型[9]。目前，常见的傅里叶型光谱测试[10]中光谱的标定与重建是采用标定波长在区间中的两个特征位置实现的[11]。对于单一特征波长的测试而言，该种方法是适用的，而且简单方便[12]；但存在多个特征波长时，该种方法从工作原理上就存在明显的误差引入。已有的报到中多采用单一波长标定的方法，或应用Mertz法校正相位误差。采用单一特征波长的测试，虽然方法简单易行、运算量小，但缺点是当存在多个特征波长时，无法同时对多个波长进行校正。本文主要针对多波长入射条件下的光谱校正与重建，提出了一种新型的多光谱数据处理算法，该算法可以在基本不改变总运算量的前提下同时对多个特征波长进行校正与重建。

1 系统设计

系统由光学天线、傅里叶干涉具、聚焦透镜组、CCD、DSP6713(DSP，digital signal processing)及显示单元组成[13]，如图1所示。测试用的半导体激光器的中心波长为632.0、650.0和660.0 nm。光学天线收集待测光进入系统，通过傅里叶干涉具完成相干处理，然后由CCD将干涉条纹采集传输给DSP6713，在处理系统中完成条纹滤波、抽样及分组，然后再由改进型Mertz法对各个特征波长的光谱数据进行校正，实现多光谱同时校正与重建。

图1 基于改进型Mertz法的多特征波长校正与重建系统Fig.1 Multi-feature wavelength correction and reconstruction system based on the improved Mertz method

线阵CCD采集的干涉条纹进入DSP后，对混合了三个特征波长的光源进行分析处理，即分别对各个特征波长的光谱进行相位校正。在本系统中采用的是静态傅里叶干涉具，属于空间干涉条纹的处理。对于不同波长的光而言，其构成的相位误差是不同的，所以本系统设计了一种改进型Mertz法，用于对多个特征光谱分别进行校正与重建。

2 高速采集模块

高速采集模块的硬件连接主要通过TTL/LVDS与McBSP，LVDS/TTL与EMIF实现。其中，LVDS/TTL与EMIF的数据通信由DMA完成。因为线阵CCD的Camera-Link接口为LVDS信号，所以是不能与DSP直接通讯的。在本系统中采用DS90CR286实现对应的电平转换，再与EMIF数据总线相连完成数据通信。其中，DMA将源地址定义为外部存储地址。由CCD获取的数据可以导入虚拟存储区，再通过DSP的内核完成光谱数据的分析与处理。此设计不需要增加FIFO结构同样可以完成数据的缓冲，不需要进一步增加运行时间。因此，该种设计可以快速的完成数据处理，结构简单，速度快。

3 改进型Mertz法

对采集得到的干涉条纹进行光谱分析，可以获得其对应的光谱分布。对于傅里叶系统而言，其干涉图的光强分布为：

(1)

其中，v表示波数，x表示对应位置。

设某一波长位置上产生的相位误差为θx(σ)，则可以将不同波长对应的相位误差分别表示为θx1(σ)、θx2(σ)、…θxi(σ)，则式(1)可表示为

I(t)=Ix1(t)+Ix2(t)+...+Ixi(t)

且

(2)

光强分布经Fourier变换后，有

(3)

包含相位误差的光谱分布，有

(4)

式(1)、(2)与(3)、(4)的变换就是空间干涉条纹与频域光谱的之间的转换。通过采样将干涉条纹转换成实序列，再通过FFT计算得到光谱数据，并在光谱分布重建中，将不同相位误差的参数分别代入光谱函数中即可。

Mertz法常用于频谱相位校正。在单波长相位校正中，用Mertz法对线性相位误差进行校正很实用。但，对多特征波长并不适合直接使用Mertz法。本文在传统Mertz法基础上，通过采用DSP中的不同寄存器进行交替参数变化，设计了一种改进型Mertz法，以实现对不同波长校正参数的调整。算法采用相同运算规则对特征波长进行处理，但在波长变换时采用多寄存器流水操作，调制运算参数，实现对不同波长的分类处理的。改进型Mertz法的运行时间与传统方法基本一致，其流程如图2所示。

图2 改进型Mertz法程序流程图Fig.2 Program flow chart of modified Mertz method

改进型Mertz算法具体步骤如下：

1)对所有数据点循环检测，寻找干涉条纹数据中的极值点，根据特征周期数分析特征波长个数，然后设定极值点个数；

2) 以每个极值点为中点进NUFFT行运算，由此可以得到其对应的实部Re(σ)和虚部Im(σ)，则其相位误差为:

(5)

3) 对所有干涉数据进行插值补零处理，从而得到校正后相位误差θi(σ)。计算其光谱：

B(σ)=Re[B′(σ)]cos[θi(σ)]+

lm[B′(σ)]cos[θi(σ)]

(6)

采用本算法可以有效地抑制由于零点偏移造成的相位误差，即不同波长在同一干涉系统中产生的误差。由此可见，算法实现了多个波长同时存在条件下的分别处理，提高了系统光谱的可分性。从运行速度上看，本算法需两次FFT、一次插值运算和两次乘法运算。与传统算法相比，在不增加运算时间的前提下，本算法抑制了多波长光谱重建中的误差。

4 实 验

实验采用基于DSP6713的处理系统，以及Roper公司CoolSNAPMYO型CCD作为传感器件，光谱范围为400～1 000 nm，像元数为1 940(1 460，单个像元尺寸为4.54 μm×4.54 μm。待测激光选用GYL@632 nm 、GYL@650 nm和GYL@660 nm型激光器，对比用光谱仪选用Bruker公司Tensor-27型光谱仪。

4.1 干涉条纹滤波

因为本文设计的多光谱测试系统针对的是脉冲激光信号，并非连续光信号，所以CCD采集的图像中会每隔一定时间有背景光噪声出现。相比待测光源而言，这些背景光是缓变信号，也就是实验环境下的背景光，在本系统中采用低频滤波的形式消除。与此同时，干涉条纹图中还存在频率较高的散斑噪声[14-15]，而条纹信号相比散斑噪声频率较低，故可采用低通滤波消除，即只保留一定范围的低频分量，滤掉其中的高频分量。实验分别对未加滤波算法和加入滤波算法的干涉条纹图像进行了对比，结果如图3所示。在本系统中采用了抽样平均滤波的方法，对干涉条纹数据先进行抽样提取再平均，抽样间隔依据各特征波长的时间周期设定，当对每个特征波长数据均遍历抽取及平均后，获得滤波后的效果。如图3(b)所示，滤波后干涉条纹中噪声减小。

图3 未加滤波与加滤波的光谱图对比Fig.3 Spectral contrast of unfiltered and filtered

4.2 光谱校正与重建

为了实现对多光谱的快速校正与重建，同时用三个中心波长不同的激光器入射系统(@632.0、@650.0和@660.0 nm)，然后在CCD上得到三组波长混叠在一起的干涉条纹。再利用上文中提到的分周期提取方法完成数据的采样，然后用不同的相位补偿参数分别对不同特征波长的干涉条纹进行校正，从而可以得到其相应的光谱分布，如图4(b)所示。而，未校正直接进行光谱反演的光谱分布如图4(a)所示。

对比图4(a)和图4(b)可以看出，未校正的光谱分布图虽可以看到三个特征波长位置，但其峰值半宽大、旁瓣噪声明显，光谱可区分度较低。尤其是当两个特征波长的中心位置较近时，主峰更是难以分辨。相比之下，光谱分布数据经过校正后，每个特征波长光谱振幅的绝对值虽然略有降低，但其锐度提高，旁瓣噪声的降幅更大，即其信噪比提高了、且光谱可区度增大。实验还采用布鲁克公司TENSOR-27型光谱仪对同一组光学信号进行了处理，其测试结果如图5所示。

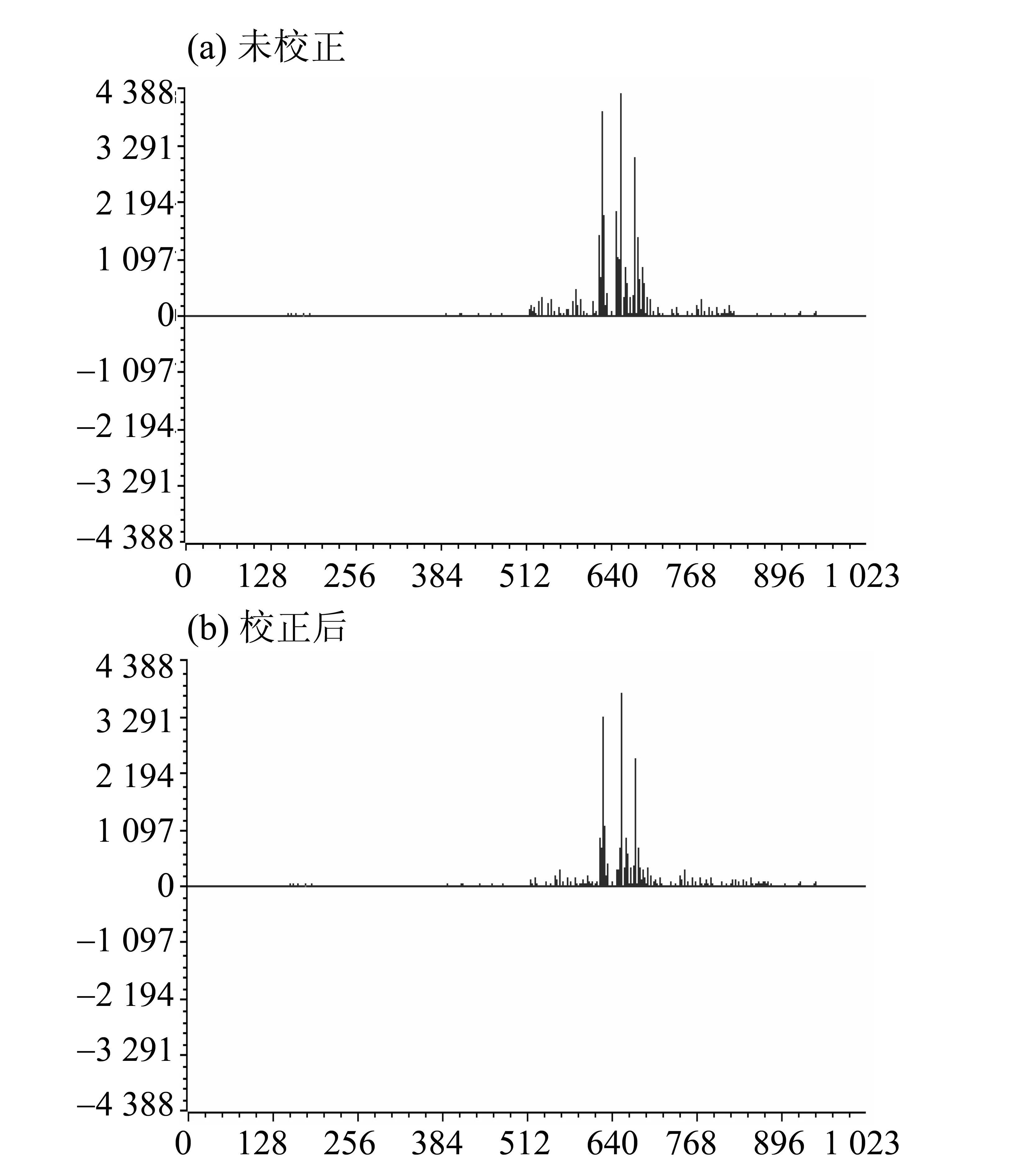
图4 未校正与校正后的测试结果对比Fig.4 Comparison of uncorrected and corrected test results

将校正后的数据与光谱仪测试数据进行对比可知，经校正后的光谱分布图与TENSOR-27型光谱仪的测试结果基本一致，三个不同中心波长的特征峰都十分明显。在632.0 nm处，本系统的测试结果为632.3 nm，光谱仪的测试结果为632.10 nm；在650.0 nm处，本系统的测试结果为649.7 nm，光谱仪的测试结果为650.24 nm；在660.0 nm处，本系统的测试结果为660.8 nm，光谱仪的测试结果为660.47 nm，平均误差都在1.0 nm以内。同时，两者都具有很好的光谱区分能力，本系统的噪声集中在-30～-34 dB的范围(均值为-32 dB)，而TENSOR-27型光谱仪得到的光谱分布噪声响应集中在-28～-32 dB范围(均值为-30 dB)，可见本系统测试得到的旁瓣噪声也优于TENSOR-27型光谱仪。这说明本系统符合多光谱快速校正及重建的设计要求。如果以相同硬件在不采用本算法的条件下仅对单特征波长测试，则其平均误差小于1.0 nm，但当同时存在多个特征波长时，不采用本算法的测试平均误差为2.4 nm。因此，本算法的引入可以大幅提高多波长同时测试条件下的光谱数据重建的准确度，提高系统测试精度。

图5 TENSOR-27型光谱仪的测试数据Fig.5 Test data of the TENSOR-27 spectrometer

5 结 论

针对传统光谱分析算法中多特征波长同时反演时存在误差的问题，本文提出了一种改进型的Mertz法。该算法利用不同中心波长具有不同干涉条纹周期的特性，将不同特征波长的数据组分别进行相位校正，从而提高光谱分布反演的准确度。对三个中心波长不同的激光同时入射系统进行光谱反演，结果显示：经本算法得到的光谱分布特征峰信噪比高、噪声平均强度低、且处理速度较快。因此，本设计算法是可行的，提高了在多特征波长条件下系统测试精度。