基于零水印与脆弱水印的矢量地理数据多重水印算法*

梁伟东，张新长2,，奚旭，张鹏程

(1.中山大学地理科学与规划学院，广东 广州 510275; 2.广州大学地理科学学院，广东 广州 510006；3. 广州市城市规划勘测设计研究院，广东 广州 510060)

矢量地理数据具有精度高、更新快等优点，已被广泛用于国防科技、经济发展等各方面。同时矢量地理数据制作成本高、易于非法传播与篡改，对其版权保护与内容认证一直是信息安全领域的重点，其中数字水印技术是一种较为有效的手段[1]。现有的矢量地理数据数字水印研究，一般只针对版权保护或内容认证，若将两者相结合，对于矢量地理数据的保护将更为全面与高效，而多重水印技术目前是较好的实现方式。但现有的矢量地理数据多重水印算法主要用于版权保护[2-4]，能同时提供版权保护与内容认证的多重水印算法很少，其主要原因是：用于版权保护的水印需要强鲁棒性，而用于内容认证的水印强调敏感性，如何保证两种水印有效且互不影响是一个难点。随着数字水印技术的发展，零水印作为一种不对原始数据进行修改的新的数字水印技术[5]，具有优异的高保真度，为解决上述问题提供新的思路：利用零水印算法或相关无损嵌入技术使两种水印相互独立，二者既能正常生效又避免产生影响。

在版权保护方面，矢量地理数据零水印算法已有相关应用，算法的关键是提取与数据载体紧密相关的特征信息，包括：数据整体的各层次拓扑结构[6]与各类统计信息[7]；数据各部分特征点，通过特定方法[8]构造出的角度序列[9]、距离序列[10]、比值序列[11]和特征点平均坐标[12]等信息；以及属性信息中的要素编码序列等[13]。各种零水印算法对几何攻击、数据压缩和裁剪等水印攻击均具有一定的鲁棒性，但由于特征信息稳定性不一，鲁棒性与安全性存在一定差异。在内容认证方面，利用脆弱水印对矢量地理数据进行精确认证，可判别数据是否完整或发生变化，并定位被篡改的数据到相应的数据块、组[14-16]或节点上[17, 18]。但是，现有算法中较少能实现水印无损嵌入，可逆水印技术[19]虽然可以无损恢复数据，但是当攻击者篡改恢复后的数据，脆弱水印技术则无法有效应对，因此，目前较为缺乏一种能为矢量地理数据持续提供精确认证且无损嵌入的脆弱水印。

基于此，本文提出一种兼顾版权保护与内容认证的多重水印算法：首先对矢量图元节点数据进行分块，针对版权保护，本文分别利用道格拉斯算法和Delaunay三角网提取特征点和特征信息，结合Arnold置乱算法，设计一种鲁棒性强、容量大、安全性高的高保真零水印算法；针对精确认证，本文通过空间排序与零比特动态扩展，设计一种精确定位到点的无损嵌入的脆弱水印。本算法通过实现多重水印的无损嵌入，达到两种水印之间互不影响的目的，有效解决了前文提出的问题，有助于全面而高效地保护矢量地理数据。

1 多重水印算法设计

1.1 技术路线

本文多重水印算法以矢量图元节点数据为基础，水印构造与水印提取检验流程如图1和图2所示。

在数据分块的基础上进行多重水印构造，通过在每个分块中嵌入水印信息，增加水印的个数，可提高鲁棒水印抵抗裁剪攻击的能力以及脆弱水印定位被篡改数据的效率与精度。本文选取点约束分块法[16]对数据进行分块，该方法在面积四叉树分块法[20]基础上，将点数量大于阈值的分块继续划分，直到点的数量小于阈值。在构造零水印时，算法的关键是从数据中提取稳定的特征信息，而拓扑信息一般较为稳定。本文首先利用道格拉斯算法提取特征点，根据Delaunay三角网空外接圆和最大化最小角性质以及局部稳定性，将各三角形角度值作为数据特征信息，构造具有较高水印容量[21]和鲁棒性的零水印。在构造脆弱水印方面，为保证在各种攻击后准确地将无序的数据集合映射到有序的水印信息上，从而正确地恢复水印信息[22]，本文采用Hilbert曲线进行空间排序，构建各节点数据的空间关系；引入零比特动态扩展技术[23]，将每个节点数据产生的水印值取模，并以相应个数的0组成零比特值，生成水印序列，按实际需求加入到该点及临近点的坐标末尾。

多重水印提取与检测是水印构造的逆过程，零水印检测是将提取到的水印图像与原始水印图像进行对比，根据相似度确定版权归属，从而对数据进行版权保护；脆弱水印检测是将提取到的原始水印序列与计算得到的现有水印序列进行对比，根据其结果进行内容认证。

1.2 多重水印构造

第1步，对矢量地理数据进行预处理，包括数

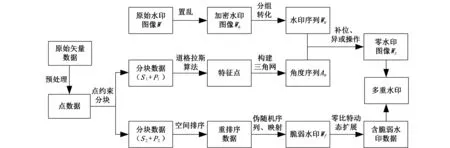
图1 多重水印构造过程Fig.1 The construction process of multiple watermarks

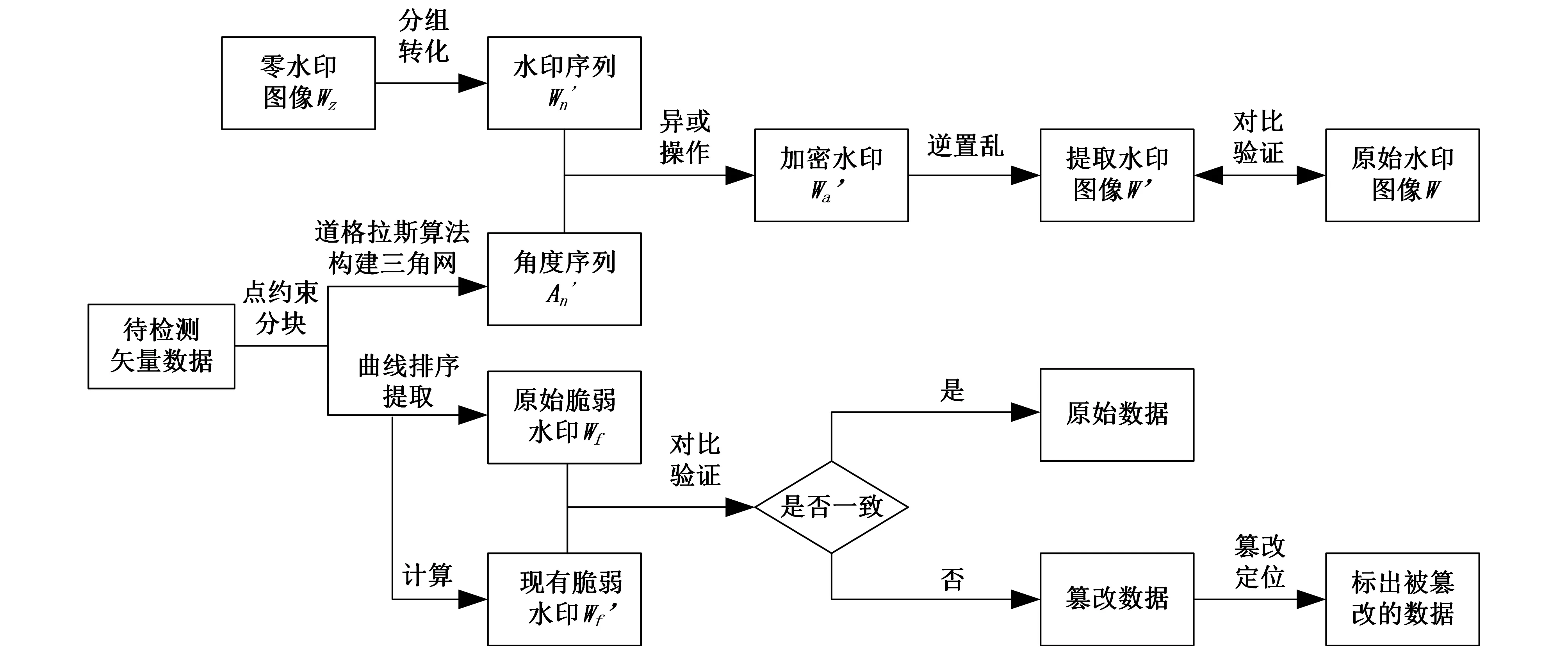
图2 多重水印提取与检测Fig.2 The process of multiple watermark extraction and detection

据检查、提取要素中各类节点数据等。

第2步，分块处理：

多重水印算法中由于功能不同，构造零水印与脆弱水印时初次分块面积分别设置为S1和S2，点个数阈值分别设置为P1和P2。

第3步，构造零水印：

1)水印图像处理：对原始二值水印图像W进行Arnold置乱，提高水印的安全性。

2)生成水印信息：将置乱水印图像，转化为0和1的有序序列，每8个值为1组，分为k组，每组序列均可转化成一个整数值n(n=0,1,…255)，将k个n值组成水印序列Wn；

3)提取特征点：对构造零水印的分块数据，选取合适的阈值，利用道格拉斯算法提取各个分块的特征点；

4)构建Delaunay三角网：由各分块特征点生成三角网，并记录各三角形的角度值，组成角度序列An，保证每个分块内的角度序列An的长度大于水印序列Wn的长度；

5)补位操作：若某分块角度序列An长度是水印序列Wn长度的a倍，则在水印序列Wn的末尾补上b个原有水印序列，如An长度为2 439，Wn长度为800，则Wn补上2Wn位，长度增长为2 400。将An与补位后的Wn进行异或操作，得到1个或a个零水印。将各个分块产生的包含若干个零水印的图像，以及原始水印图像保存至版权保护中心(IPR)，并加入具有法律效力的时间戳，抵御解释攻击。

第4步，构造脆弱水印：

1)空间排序：对构造脆弱水印的分块数据中的节点数据按照Hilbert曲线进行排序；

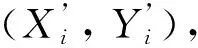
(1)

(Xz,Yz)=((f2(Xb,Yb))10)%10

(2)

c=f3(Xz,Yz)=(Xz⊕Yz)%5

(3)

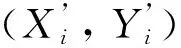
3)水印无损添加：为了有效抵抗删点攻击，对分块内任意节点Pi(Xi,Yi)及Hilbert排序中的后邻点Pi+1(Xi+1,Yi+1)，利用零比特动态扩展，将Pi的脆弱水印信息Wf，分别加入到横坐标Xi末位和Pi+1的纵坐标Yi+1末位；若Pi为分块的末点，则该点的Wf添加到分块的首点的纵坐标上。对各分块进行上述操作。

1.3 多重水印提取与检验

第1步，对待检测矢量地理数据进行预处理。

第2步，提取与检验零水印：

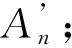
4)对比验证：将多个提取水印图像W’与原始水印图像W进行验证，利用归一化相关系数NC值(Normalized Correlation)衡量两图像相似性，公式如下：

(4)

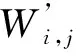
第3步，提取与检验脆弱水印：

1)待检测数据处理：按照与前文相同的方法，对待检测数据进行分块、Hilbert空间排序处理；

2)提取水印处理：从各分块内提取任意节点Pi(Xi,Yi)坐标末尾的原始脆弱水印信息，记横坐标提取到的水印信息为Wf，后邻点Pi+1(Xi+1,Yi+1)纵坐标提取到的水印信息为Wf+1；

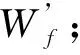
2 实验与分析

本文提出的多重水印算法，可应用于各类点状数据、线状数据和面状数据中，其中，线状数据需要提取各图元中的节点数据，面状数据可转化为线状数据再提取节点数据。本文选取广州市海珠区1∶5 000 Shp格式的道路矢量数据作为实验数据，其中，线状要素共15 791条，预处理后数据点总个数为50 717个。

2.1 零水印实验

本文选用写有“中大地规院”的二值图像作为原始水印，大小为80×80，水印序列Wn的长度为800。对节点数据进行点约束分块处理，初次分块面积为总面积的1/4，点个数阈值P为5 000；道格拉斯算法提取特征点的阈值为500 m，共提取7 976个特征点，压缩比为84.27%；通过构建Delaunay三角网以及角度序列与水印序列的异或运算，最终获得18个分块和32个零水印，可证本算法容量较大。本次实验利用NC值与还原的零水印个数，综合衡量该算法能否抵御各种常见的水印攻击，其中NC值阈值设定为0.8。

(1)唯一性验证

由于零水印并不直接添加到原始数据中，且数字水印必须是唯一的，因此需要检验本算法构造的零水印是否具有唯一性。检验方法是，选用广州市天河区和越秀区的道路矢量图作为对照，与海珠区道路矢量数据构造的零水印进行提取水印操作，结果如表1所示。作为对照的两组数据NC值均小于阈值，即水印验证失败，本算法构造的零水印具有唯一性。

表1 零水印唯一性验证结果Table 1 The result of zero-watermarking uniqueness verification

(2)几何攻击

几何攻击包括：平移、旋转、缩放和裁剪等攻击手段，是矢量地理数据的常见操作。由于矢量地理数据的中各要素的拓扑关系具有平移、旋转、缩放不变性，本算法零水印是基于拓扑关系构造的，因此这3种攻击手段对水印信息验证没有影响。对实验数据分别裁剪25%(A1)，50%(A2)和75%(A3)，对裁剪后的数据提取水印，结果如表2所示。由于本文算法构建了多个零水印，且均匀分布于数据中，可有效抵御裁减攻击。

(3)数据编辑攻击

数据编辑攻击包括：增加节点、删除节点等攻击手段。对实验数据分别增加与删除1 000个(B1、C1)、3 000个(B2、C2)和5 000个节点(B3、C3)，对编辑后的数据提取水印，结果如表2所示。随着删除点个数增加，NC值与还原的零水印数量有所下降，即部分特征点也被删除，但由于本算法已构建Delaunay三角网，部分节点增加或删除，只影响临近的三角形，因此，本文零水印算法对数据编辑攻击具有较强鲁棒性。

(4)数据压缩攻击

道格拉斯算法是常用的数据压缩方法，对实验数据分别进行25%(D1)，50%(D2)和75%(D3)的压缩攻击，提取水印后，结果如表2所示。由于本文零水印算法设置了比正常压缩程度更高的阈值，对数据压缩攻击具有很强的鲁棒性。

(5)数据转换攻击

数据转换攻击包括数据投影转换和数据格式转换，其中数据投影转换较为常用。实验数据采用WGS-1984-UTM投影坐标，我国常用的坐标系包括CGCS2000坐标系、西安80坐标系(E1)和北京54坐标系(E2)，由于实验数据所在区域WGS84坐标系与CGCS2000坐标系误差极小，不具有实验意义，故只对其余2个坐标系进行投影转换检验，分别提取水印后，结果如表2所示。由于投影变换对数据点操作强度较大，造成NC值较低，但仍然大于0.8，可证本文零水印算法对数据转换攻击具有较强鲁棒性。

(6)组合攻击

组合攻击是指对实验数据同时使用多种攻击手段的综合性攻击，由于攻击手段未知，且同时进行攻击，抵御难度较大。本实验选取地图综合中的简化路网作为组合攻击，包括2个内容：去除实验数据中的“环岛”与匝道(F1)，并在此基础上删除部分低等级道路(F2)。进行上述操作后，分别有约2 000个和10 000个数据点被修改，提取水印后，结果如表2所示。根据实验结果，本文零水印对组合攻击具有一定鲁棒性，但随着攻击强度增大，鲁棒性有所下降。

表2 数据裁剪、编辑、压缩、转换攻击和组合攻击结果Table 2 The result of data cropping attack, editing attack, compression attack, transformation attack and combination attac

2.2 脆弱水印实验

对节点数据进行点约束分块处理，综合考虑精确认证以及篡改数据定位的效率与精度，初次分块面积为总面积的1/64，点个数阈值P为1 000。本算法采用零比特动态扩展，实现脆弱水印无损嵌入，具有良好的不可见性。为检验本算法的准确性，对已加入脆弱水印的实验数据不作任何修改并进行精确认证，认证结果通过，可证算法具有可行性。

(1)增点攻击

对加入脆弱水印的矢量数据增加1条包含10个节点的线要素，进行水印提取与验证，增点攻击没有通过脆弱水印的精确认证，并有效检测到新增的点要素，结果如图3所示。由于增加的点要素不包含脆弱水印信息，因此，不能提取原始水印信息Wf，这是增点攻击区别于其他攻击的明显特征；另外结合属性信息中的重要字段等进行判别可起到辅助作用。

(2)删点攻击

对已加入脆弱水印的矢量数据删除某段道路及其所有节点，进行水印提取与验证，结果如图4所示。删点攻击没有通过脆弱水印的精确认证，并有效检测到被删除的点要素，标注出其前邻点和后邻点，达到水印抗删除的预期效果。由于经过空间排序，被删除点要素的前后邻点并不一定是所在线要素的起点与末点，因此本实例具有两个前邻点与后邻点，且空间上没有关联性。

(3)平移攻击

对已加入脆弱水印的矢量数据进行整体平移与局部平移，并进行水印提取与验证。平移操作实质上是对数据点的坐标进行修改，基于坐标值的原始水印信息也相应发生变化，因此，数据整体平移后，超过90%的点要素被标记；局部平移的点要素也被标记，如图5所示。

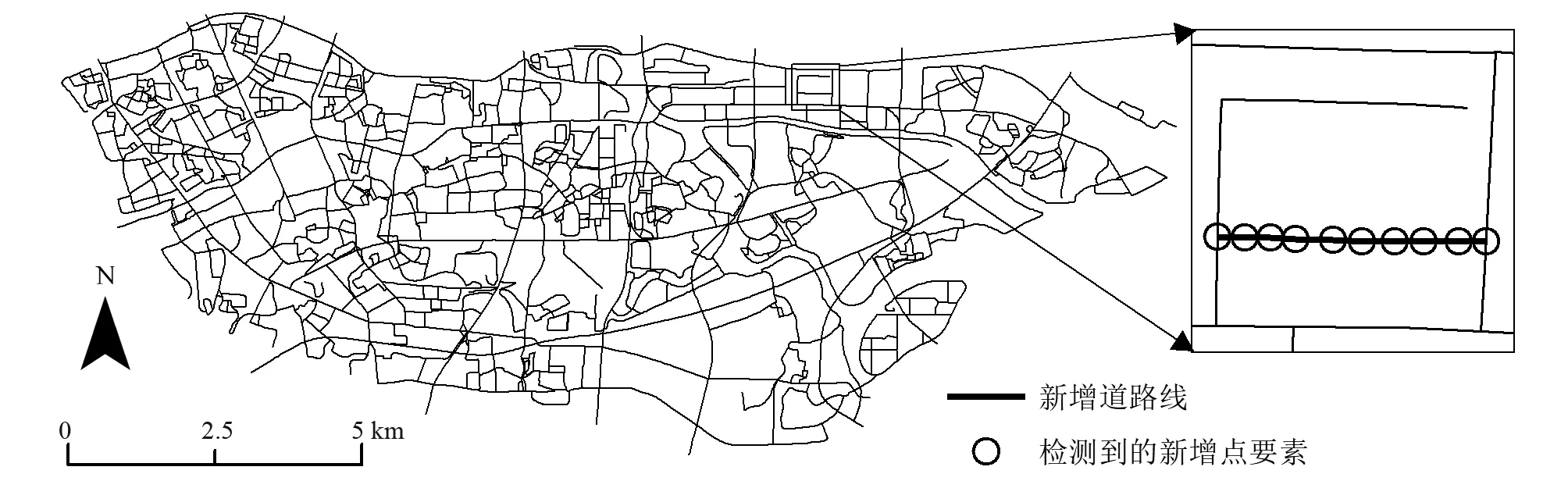
图3 增点攻击结果Fig.3 The result of adding elements attack

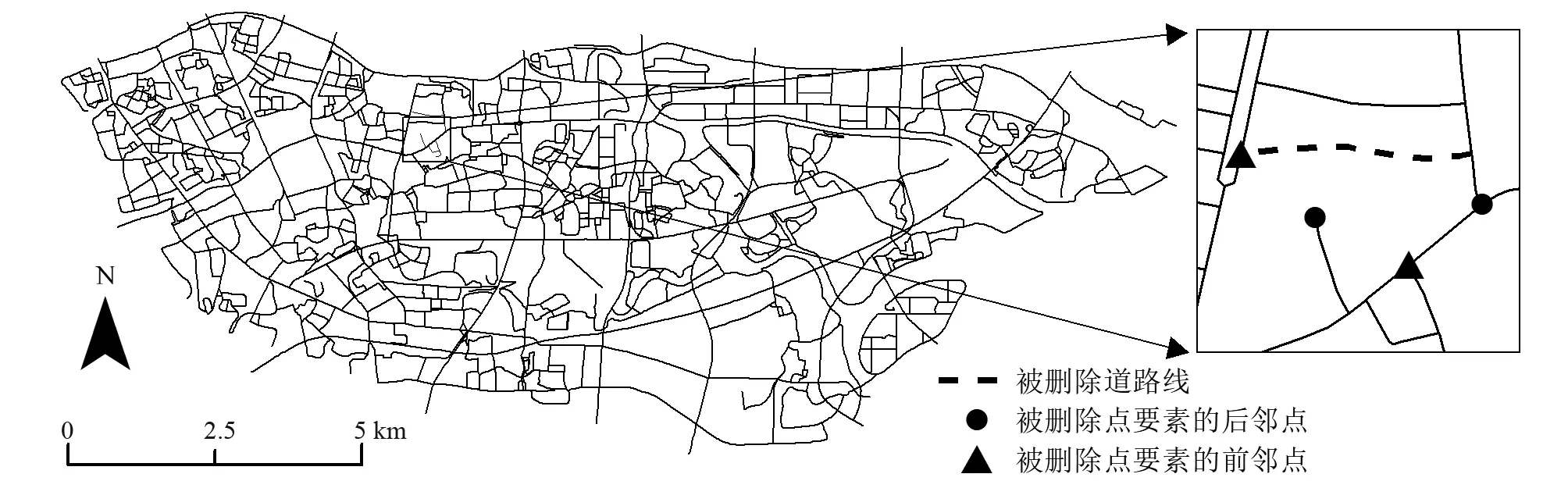
图 4 删点攻击结果Fig.4 The result of delecting elements attack

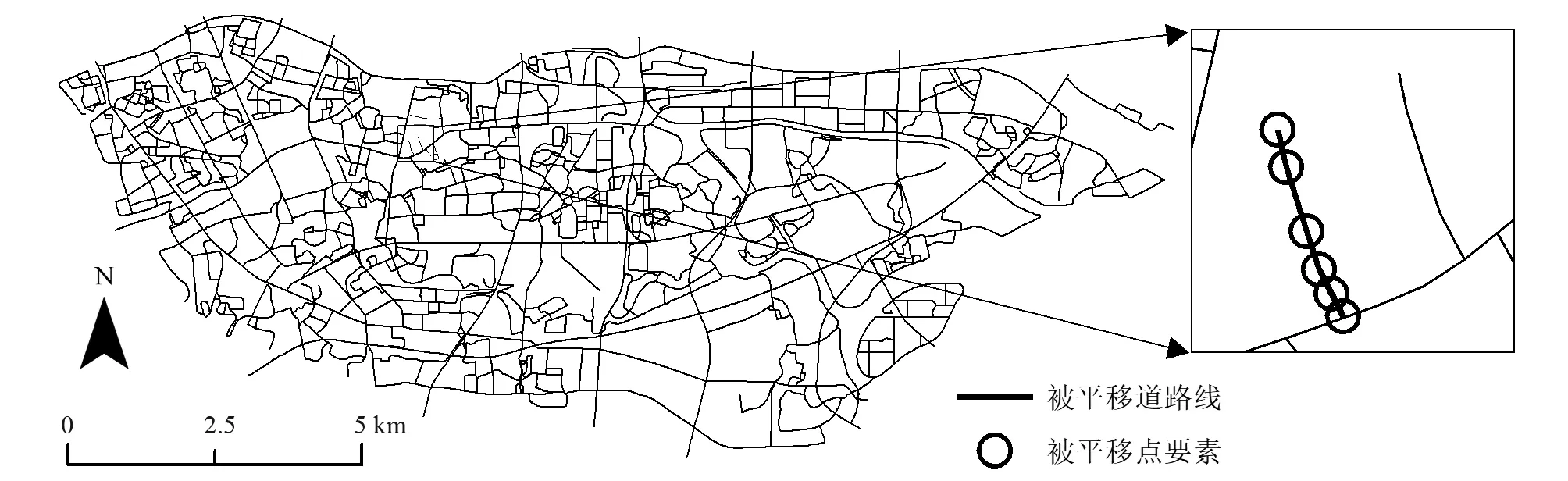
图5 平移攻击结果Fig.5 The result ofatranslation elements attack

3 结 论

本文基于矢量图元节点数据，提出一种基于零水印与脆弱水印的多重水印算法，一方面将鲁棒水印与脆弱水印相结合，利用零水印和无损嵌入技术解决了两种不同性质水印互相干扰的问题，达到兼顾数据版权保护与精确认证的目的；另一方面，本算法对水印的提取与验证，无需原始数据参与，是一种盲水印，具有较高实用性。根据水印的特点与功能，本算法进行不同尺度的数据分块，结合道格拉斯算法和Delaunay三角网分别提取具有代表性的特征点和稳定的特征信息，构造出容量大、安全性高的零水印，并对几何变换、数据编辑、数据压缩、数据转换以及综合攻击具有较强鲁棒性，可有效保护数据的版权；在精确认证方面，本算法利用空间排序的方法，建立各分块内节点数据间较为稳定的空间关系，并尝试将脆弱水印与零比特动态扩展技术相结合，在确保水印信息对数据的精度与使用没有造成任何影响的同时，对数据的真实性和完整性进行有效判别，能精确定位被篡改的部分数据到数据点，满足实际应用需求。

由于将脆弱水印信息加入到坐标值末尾，本文算法与文献[16-18]的算法均对精度约减攻击抵抗较弱，水印可能会被整体破坏；另外，现有的精确认证算法还不能有效判别常见的攻击类型。下一步研究工作的重点将放在选取更稳定安全的脆弱水印嵌入方式，以及分析记录常见攻击类型的特征，希望有所收获。