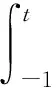
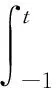
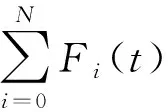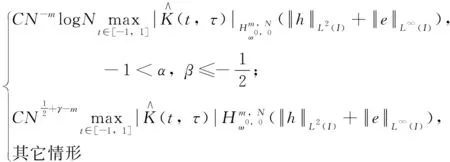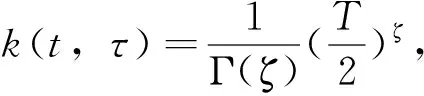比例延迟分数阶Volterra型方程的谱分析*

郑伟珊

(韩山师范学院数学与统计学院，广东 潮州 521041)

Volterra型方程作为数学模型出行在许多应用领域中，如通信系统[1]，水文模型[2]，生物种群问题[3]等等。然而早期关于该类方程的研究都是理论分析居多，随着社会经济的发展，科学研究逐步深入，由实际问题导出的模型越来越复杂，呼吁着高效分析方法的产生。关于Volterra型方程收敛性分析，受到广泛的关注[4-13]，如线性多步法[4]，逐片多项式法[5]，HP间断Galerkin法[6]，谱配置法[8-11]，其中谱配置法具有高效的指数收敛速度已被大量应用于解决各类整数阶Volterra方程，这里仅列举各类方程的一个代表：积分方程[8]、微积分程[9]、弱奇异核方程[10]、非线性方程[11]，其中包含延迟的情形[8-10]，然而这些都是整数阶情形，该类方程的分数阶类型研究不多[12-13]，而分数阶微积分方程因更好地刻画和描述了自然现象、动态系统的变化过程近几年来得到了广泛的应用[14-16]，故本文在已有整数阶Volterra方程研究的基础上将其推广至被积函数带比例延迟的分数阶情形，方程形式如下

(1)

其中G与K为已知足够光滑的函数，0<ρ，ζ<1,H(x)未知且H0是已知常数，Dζ表示ζ阶Caputo分数阶导数，在本文具体为

(2)

相应的Riemann-Liouville分数阶积分为

(3)

Γ(·)为Gamma函数。方程(1)的初始条件结合式(2)和式(3)可以得到

(4)

为了进行谱分解，必须对式(1)和式(4)进行变量代换，令

倘若记

则

Dζh(t)-h(t)-

(5)

h(t)-h(-1)=

(6)

其中t∈[-1,1]，令

表示一组配置点，它是N+1个Jacobi-Gauss点，相应的权记为ωα，β，则方程(5)和方程(6)在配置点ti上显然成立

Dζh(ti)-h(ti)-

(7)

h(ti)-h(-1)=

(8)

为了获得更高的精度，需进行适当的线性变换，为此令

(9)

其中-1≤θ≤1，若记

则方程(7)和方程(8)可以重记为

Dζh(ti)-h(ti)-

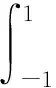
(10)

h(ti)-h(-1)=

(11)

Dζh(ti)-h(ti)-

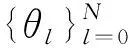
h(ti)-h(-1)≈

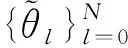
记

hi≈h(ti)，Dζhi≈Dζh(ti)，

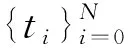
F(ρτ(ti,θl)+ρ-1)ωl=g(ti)

(12)

hi-h(-1)=

(13)

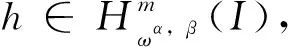
1 若干引理

引理1[17]假设用带Jacobi权N+1个点的Gauss积分公式计算hφ的积分，φ∈PN，则

其中

(14)

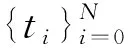
(15)

且

(16)

(17)

引理3[19-20]对于一个非负整数r和κ∈[0,1]，存在一个常数Cr,κ>0，使得对于任意函数v∈Cr,κ([-1,1])都存在一个多项式函数TNv∈PN，有

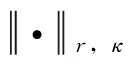
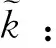
则对于任意函数v∈C([-1,1])，都存在一个正的常数C使得

引理5[22]对所有可测函数f≥0，当1

成立当且仅当

这里的函数T是一个算子

其中函数k(t,τ)是一个给定的核函数，u和v都是非负的权函数且-∞≤a

引理6[23]对于每个有界函数v，有

2 结 论

定理1 令h(t)是方程(5)-(6)的解，并假定足够光滑，若DζF(t)是通过谱方法由方程(12)和方程(13)获得的逼近解及逼近导数，0≤ζ<1，其误差函数为Dζe(t)=DζF(t)-Dζh(t)，则当N足够大有

这里

证明利用离散内积记号(14) 可以把方程(12)重记为

Dζhi-hi-(k(ti,τ),F(ρτ+ρ-1))N=g(ti)

若记

J(t)=(k(t,τ),F(ρτ+ρ-1))N-

(k(t,τ),F(ρτ+ρ-1))ω0,0

则还可将上式记为

Dζhi-hi-(k(ti,τ),

F(ρτ+ρ-1))ω0,0-J(ti)=g(ti)

(18)

再由式(9)知，式(18)和式(13)分别可以化为

Dζhi-hi-

(19)

hi-h(-1)=

(20)

Dζe(t)=

(21)

e(t)=

(22)

这里

I3(t)=INDζh(t)-Dζh(t)，

根据Dirichlet公式

得

Dζe(t)≤

(23)

其中C1是正的常数, 而

因为0<ρ<1，ρt+ρ-1=ρ(t+1)-1

(24)

再由式(22)有

(25)

综上得

(26)

再利用引理2的式(15)，有

(27)

又由引理2的式(17)有

(28)

(29)

再次利用引理2中的式(17)，令m=1，有

(30)

(31)

最后一个不等式，在以下情况下使用引理4

综上分析由式(27)-(31)，定理第一个结论获证。下面再由式(23)，利用Gronwall定理及引理5有

(32)

由引理6可得

(33)

再由引理2的式(16)可以得到

(34)

对于I4(t)的估计，使用引理2的式(16)并令m=1时，得

(35)

对于I5(t)的估计，借助引理3，引理4和引理5，且当κ∈(0,1-μ)有

(36)

式(33)与式(36)利用定理第一个结论，令m=1即可得定理第二个结论。