回顾生物科学史,突破遗传规律教学难点

宋立伟

(黑龙江省大庆实验中学 163316)

“孟德尔的豌豆杂交实验(一)”是人教版高中生物学必修2教材《遗传与进化》第1章第1节的教学内容。教材中介绍了孟德尔采用科学的统计学方法，在豌豆F2中得到3∶1性状分离比的基础上揭示了分离定律。然而，教学中很多学生对“孟德尔仅仅是看到了3∶1的性状分离比就得出遗传因子的特点、存在方式及如何向后代传递”表现出疑惑和质疑，不清楚孟德尔是如何推理的。为解决这个问题，教学中可适当还原孟德尔豌豆杂交实验的具体内容，以加深学生对孟德尔建立假说的核心思想及假说内容的理解。

1 1∶2∶1比值的发现

自1854年开始，孟德尔以豌豆为实验材料进行了一系列的遗传学实验，时间长达10年。1865年孟德尔公布所发现的遗传学规律，并于1866年以德文在《自然史学会杂志》发表了论文。孟德尔在豌豆杂交实验中分别观察了植株高矮等7对相对性状，通过一粒一粒、一株一株地进行计数，孟德尔发现这7对相对性状的杂交实验中，F2个体中性状分离比均接近3∶1，后人把这一比值称为“孟德尔比数”，用现代遗传学的语言描述即为： F2表现型中显性性状与隐性性状的分离比为3∶1。据此孟德尔认为隐性性状没有因在F1个体中不表现而消失，即融合遗传的观点是错误的。孟德尔强调，3∶1比例毫无例外地适用于所有(7对)性状。然而3∶1这一比值背后到底隐藏着什么奥秘呢？

在得出3∶1性状分离比后，孟德尔的一对相对性状杂交实验就到此结束了吗？孟德尔仅仅是根据3∶1就建立了被后人称为分离定律的假说？答案当然是否定的。在得出3∶1的性状分离比后，孟德尔对F2豌豆继续进行自交实验，结果显示F2中表现型为隐性性状的个体在F3中不再有性状分离。然而，F2中表现型为显性性状的个体自交得到的结果则不一样，F2中显性性状的个体自交后有1/3个体的后代保持了显性性状的稳定，而另外2/3个体自交产生的后代中再次出现显性性状： 隐性性状=3∶1的分离比(表1)。由此可见，F2中显性性状可以有两种意义，既可以是亲代“恒定”性状(纯合子)也可以是F1代的“杂交体”性状(杂合子)，且“恒定”性状：“杂交体”性状=1∶2。这是为什么呢？难道是偶然或个别的现象吗？为此，孟德尔将7对相对性状杂交实验中的F2均进行了自交，其结果均表现为F2显性性状的个体中“恒定”性状与“杂交体”性状数目比均为1∶2。因此，F2性状分离比3∶1中的“3”尽管都表现为显性性状，但是其“内部”是不一样的，其可分为稳定的显性性状类型和杂种的显性性状类型，且比例为1∶2，以后各代无不如此。因而，孟德尔指出在F2中性状分离比3∶1可分解为1∶2∶1。

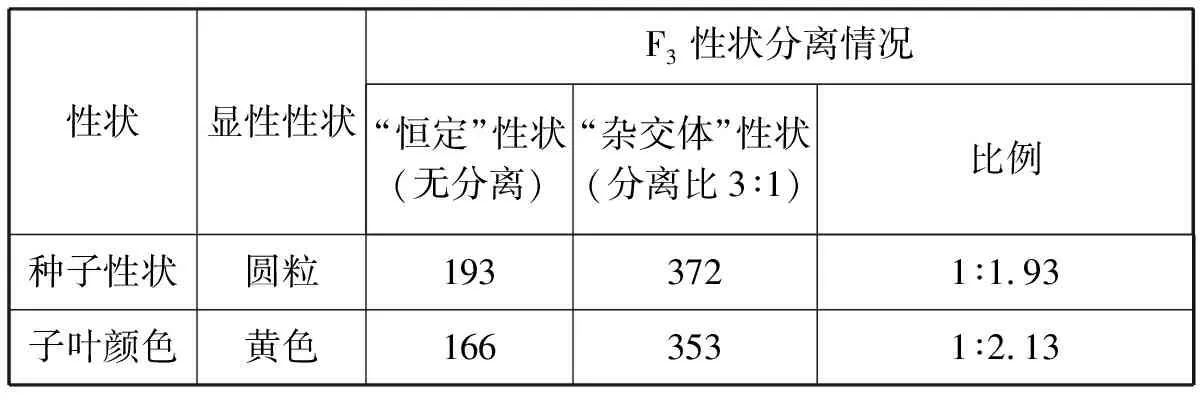
表1 孟德尔豌豆杂交F2显性性状分离的实验结果

2 1∶1比值的发现

通过子代的性状及进一步的杂交实验推出1∶2∶1规律后，孟德尔继续探索1∶2∶1比值背后的真实原因。经过深思熟虑及结合他人的研究成果，孟德尔认为子代性状的差别及比值实际是由生殖细胞组成的差别所造成。孟德尔敏锐地从3∶1和1∶2∶1这两个比值中看出了1∶1的比数。尽管在其《植物杂交的实验》一文中没有出现1∶1这样的数学式，但其论文中有几处表达了同样的意思，如孟德尔在其论文中写道：“只要我们同时假定杂种所形成的不同种类的卵和花粉其平均数目相等，就足以解释各代杂种发育的情况。”这不就是清楚地表明了1∶1的比值嘛！那么，孟德尔又是如何建立起1∶1与3∶1、1∶2∶1的联系呢？

3 建构数学模型解释分离现象

F2出现3∶1的性状分离比，显然融合遗传的观点已经无法给出合理的解释，因此孟德尔在观察和统计分析的基础上，通过严谨的推理和大胆的想象，根据杂合子的配子分离比1∶1及子代的表现型3∶1、1∶2∶1三个比值的内在联系推理出了遗传因子的特点、存在方式及向后代的传递方式。

孟德尔推测花粉细胞有A、 a两种且数量相等，卵细胞也有数量相等的A和a两种，同时不同类型的花粉细胞均有同等机会与不同类型的卵细胞组合，正是因为F1形成带遗传因子A的配子与带遗传因子a的配子的比数是1∶1，受精后才形成F2中AA、 Aa、 aA、aa四种类型，因为Aa的性状相同于aA(仅A和a来源的父本、母本不同)，它们都表现为显性性状。所以，AA+Aa+aA+aa=AA+2Aa+aa，而AA与Aa表现出来的性状是一致的，这样F2个体中表现型为显性性状和隐性性状的比例才为3∶1，且可分解为1∶2∶1。最后，孟德尔设计了测交实验验证了杂合体产生2种花粉细胞或卵细胞的比例都为1∶1。因此，1∶1是最根本的孟德尔比数，3∶1和1∶2∶1都是由1∶1衍生的。至此，孟德尔把理论深入到生殖细胞，并且运用两数和的平方公式模型解释遗传学的规律，模型虽简单却揭示了遗传学的奥秘。

综上，教师在生物学教学中可为学生介绍以上孟德尔发现的3∶1、1∶2∶1、1∶1这三个比值的简要过程，这样学生不仅可深入地理解孟德尔建立的假说内容，也可为后续学习自由组合定律奠定较为坚实的基础。