基于系统聚类的我国城市轨道负荷强度分析

张俊锋

（中国铁路设计集团有限公司，天津 300142）

伴随我国经济的持续快速发展与城镇化进程的不断推进，近年来，我国城市轨道交通快速发展。由于城市轨道交通项目投资大、费用高，自身经济效益差，建设运营存在一定风险，合理控制建设规模和发展速度极为重要。因此，在规划设计阶段合理把控城市轨道交通网络规模具有重要现实意义。

城轨线网规模计算方法主要包括因素分析法、服务水平法、出行需求法和回归分析法等。其中,需求分析法应用最广泛，其关键在于合理把控研究年度城轨网络负荷强度，结合城轨客运总量匡算网络规模。

现有研究对城轨负荷强度的确定多参照国外相关城市和我国北京、上海等大城市的负荷强度。这样虽具备一定合理性，但国外城市的人口密度、机动化程度、城市布局等与我国差别很大，应用国外经验还需进一步研究。而北京、上海作为我国经济最发达、人口最稠密的城市，直接参考其城轨负荷强度显然也是不合适的。

截至2017年末，我国内地已有34个城市开通城轨交通，为研究我国不同类型城轨负荷模式提供了丰富的研究样本。因此，本文应用系统聚类法，结合城轨相关统计数据以及城市经济、人口、机动化水平等因素，对现状我国城轨负荷模式进行分类、分析影响其负荷强度的深层原因，为规划设计中确定城轨负荷强度、匡算城轨网络规模提供参考依据。

1 系统聚类法

1.1 系统聚类基本思想与步骤

系统聚类法是将性质相近的个体归为一类，使得类内个体具有较高同质性，类间个体具有较高异质性。设n个样品的p维观测数据组成一个观测矩阵X：

式（1）中：xij为第i个样本xi第j项指标的观测值。

聚类开始时将n个样本各自作为一类，并计算样本之间的距离和类之间的距离，将距离最近的两类合并为一个新类，计算新类与其他类之间的距离，重复进行两最近类的合并，直至所有样本合并为一类。

1.2 样本距离与类距离

记样本xi与样本xj间的距离为dij；聚类过程中，类GK与GL类间的距离为DKL.

选用欧氏距离表示样本间距离，第i个样本xi与第j个样本xj的欧氏距离定义为2，…，n；j=1，2，…，n.

类平均法很好地利用了所有样本之间的信息，被认为是一种较好的聚类方法。GK与GL之间的平方距离定义为，类间平均距离的递推公式为

1.3 聚类效果评价指标

聚类效果的好坏用Cophenetic相关系数来反映，其值越接近于 1，聚类效果越好，即 y=[y1，y2，…，yn（n－1）/2]为样本对距离向量，d=[d1，d2，…，dn（n－1）/2]为 cophenetic 距离，其中dn（n－1）/2为第n个样本与第n－1个样本初次并为一类时的并类距离。Cophenetic相关系数为：

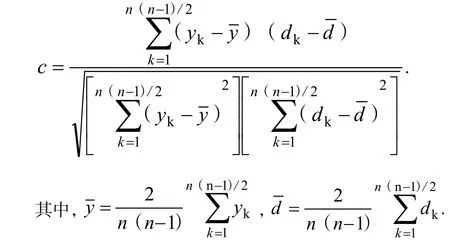
2 样本与聚类指标选择

2.1 样本选择

城市轨道交通客运量发展与开通年限有关，为了避免居民出行惯性的影响，按2017年统计数据，选择城轨运营超过3年且数据完整城市作为研究样本：北京、上海、天津、重庆、广州、深圳、武汉、南京、沈阳、大连、成都、西安、哈尔滨、苏州、昆明、杭州、长沙、宁波、无锡、南昌、青岛，共计21个城市。

2.2 聚类指标选择

城轨负荷强度是城市轨道供给与城市交通需求综合作用的结果。因此，选择客运总量（万人次）、客运周转量（万人·km）、客运强度（万人次/d·km）、乘客平均出行距离（km）描述城轨运营特点；选择运营线路长度（km）、城区线网密度（km/km2）、城区人均线网长度（km/万人）来描述城轨交通供给；选择城镇人均可支配收入（元）描述城市经济水平；选择城区人均汽车拥有量（辆/人）描述城市机动化水平，共计9个指标，记为Z1，Z2，…，Z9.相关数据来源于《城市轨道交通2017年度统计和分析报告》、城市建设统计年鉴和各地统计公报。各城市相关指标如表1所示。

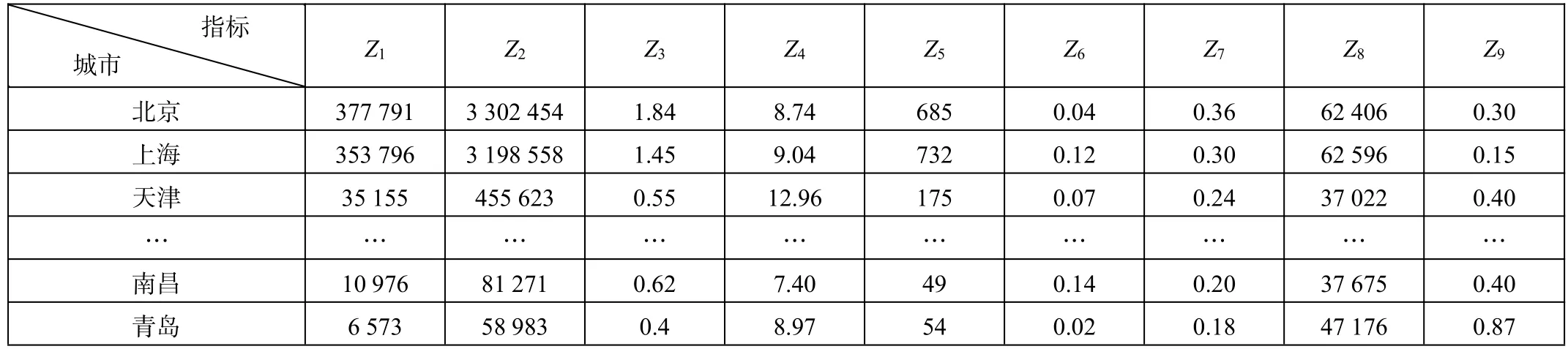
表1 各城市相关聚类指标

2.3 数据预处理

对于多元数据，为消除其各项指标量纲和数量级的限制，对数据进行标准化变换。设式（1）中的样本矩阵元素xij标准化变换后为，则有：

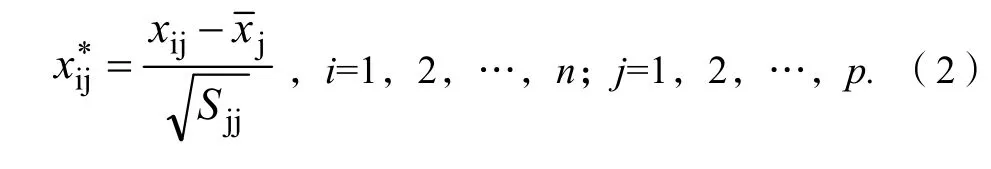
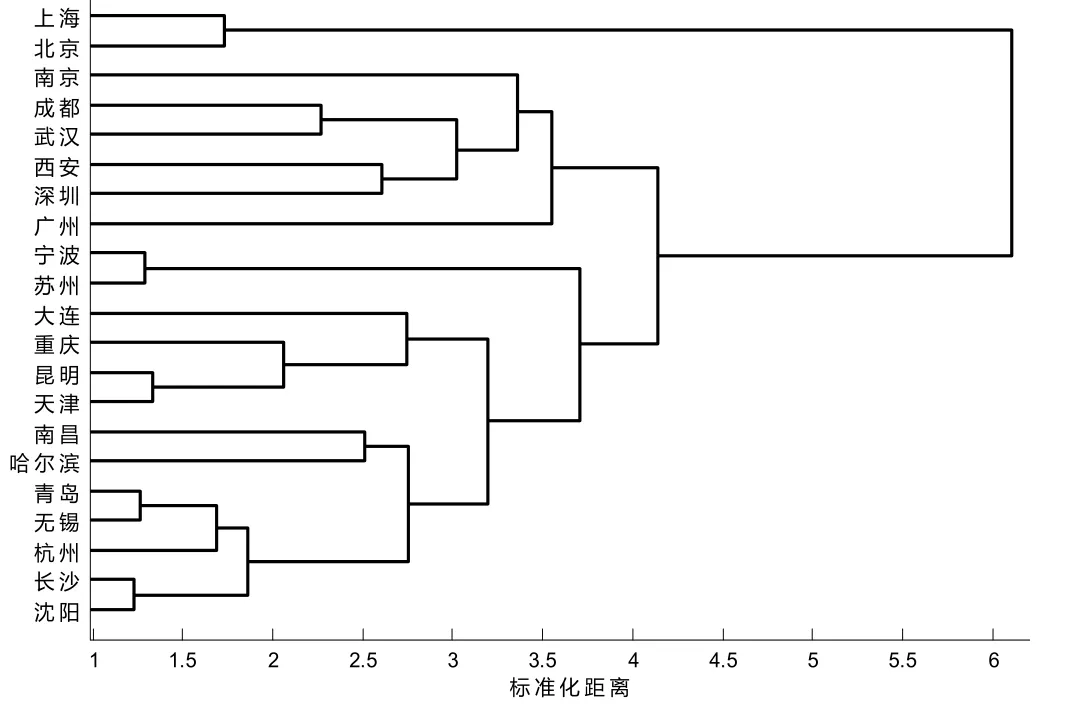
图1 各城市聚类谱系图

3 城轨开通城市系统聚类及结果分析

应用MATLAB，根据选定聚类指标使用系统聚类法对研究城市进行聚类，结果如图1所示。本次聚类Cophenetic相关系数为0.833 3，接近于1，聚类效果良好。

系统聚类后，现状开通城轨城市被分为三大类。第一类包括北京、上海；第二类包括南京、成都、武汉、西安、深圳、广州；第三类包括宁波、苏州、大连、重庆、昆明、天津、南昌、哈尔滨、青岛、无锡、杭州、长沙、沈阳。各类对应聚类指标均值如表2所示。从表2中可以看出，第一类城市的城轨负荷强度较高，客运规模最大，但其网络规模也最大。这类城市城区人口密集、经济活力强、出行需求旺盛。由于城市发展水平高，逆城市化现象明显，跨区域出行较多，平均出行距离较长，居民出行对城轨具有一定程度的依赖性。从城区线网密度和城区人均线路长度来看，属于典型低密度高负荷模式，负荷强度较高，在1.4～2.0.

第二类城市城区面积较小、城区人口较少，因此虽城轨规模较小，但其线网密度和人均线路长度都较大，属中密度供应。其平均出行距离较短，说明城市还未出现明显的功能聚集。结合其较高的城镇居民可支配收入和城区人均汽车保有量，这类城市正处于城市化快速发展阶段，居民出行对城轨已表现出一定程度的偏好。

进一步分析，该类又可分为3个子类。第一子类以广州为代表，其经济活力强、出行需求大，但城市内部城轨供给充足，属于中密度高负荷模式，负荷强度在2.0左右；第二子类包括成都、武汉、西安、深圳，经济较为发达，城轨客运规模较大，属中密度中负荷运行模式，负荷强度在1.0～1.5，其中，西安由于运营里程较短、集中服务主城核心地区，因此其负荷强度大于同类城市；第三子类以南京为代表，城区城轨密度较低，但城区人均线路长度较高，因此，仍可算作中密度，其城区人均汽车拥有量较高，城轨分担率较低，属中密度低负荷模式，负荷强度小于1.0.

第三类城市各项指标都较低，但平均出行距离和城区人均汽车保有量水平较高。除城市自身经济活力影响，现状这类城市轨道交通主要解决主城区客流走廊上的交通需求，其城市化程度较弱，城市机动化还处于依赖道路交通阶段，城轨主要承担线路两端向中心城区客流，出行距离较长。其中，哈尔滨与西安相似，由于现阶段集中服务城市核心地区，客流强度较高。综合来看，第三类城市客流强度在0.4～1.0.

表2 三类城市聚类指标均值表

4 结论

应用系统聚类法对21个开通城轨城市进行聚类，结果表明：①我国城轨负荷模式可分为三大类，五小类，分别为发达城市低密度高负荷模式，其负荷强度在1.4～2.0之间；发达城市中密度高负荷模式，其负荷强度在2.0左右；较发达城市中密度中负荷模式，其负荷强度在1.0～1.5之间；较发达城市中密度低负荷模式，其负荷强度小于1.0；一般城市低密度低负荷模式，其负荷强度在0.4～1之间。②城轨沿城市客流主通道集中供应可显著提高负荷强度，其负荷水平往往超过同类型其他城市，有助于提高城轨利用效率。③城市发展和机动化进程所处阶段对城轨负荷强度影响显著，同等城轨供应水平下，城市经济越发达，机动化进程越高，城轨负荷强度越高。

由于我国城轨仍在不断建设中，供需关系还在不断动态演进，今后，随着城轨规模的进一步扩展以及市域轨道兴起，我国城轨负荷模式可能产生较大变化，有待于进一步研究。