基于用户利益与出行意愿的电动汽车充放电调度策略*

2018-08-07杨春萍赵祺祁兵李彬崔高颖

电测与仪表 2018年8期

杨春萍，赵祺，祁兵，李彬，崔高颖

(1．华北电力大学电气与电子工程学院，北京102206;2．国网江苏省电力公司电力科学研究院，南京210003)

0 引言

文献［1］构建了用户选择充电时间对峰谷电价时段的响应模型;通过蒙特卡洛法模拟得到电动汽车充电负荷的日负荷曲线，并与原始电网负荷曲线叠加，从而形成实施效果下的电网实际负荷情况。在此基础上建立了以峰谷差率最小为目标的最优化模型，通过遗传算法对峰谷电价时段优化问题进行了求解。文献［2］利用蒙特卡洛法对大规模电动汽车接入电网充电负荷进行评估的基础上，建立了电动汽车有序充电模型。以电网负荷削峰填谷为目标，通过遗传算法建立针对电动汽车负荷的需求侧响应策略优化模型。文献［3］仿真了四种情境下电动汽车充电对电网的影响，得到在非电网运营机构会采取分批充电的模式下可以让电动汽车电池的充电功率比较均匀地分布在谷期阶段，有效地填充了负荷低谷。文献［4］提出有序充电的智能控制策略，采用中间管理者，将集中优化控制与分布式优化控制相结合。文献［5］提出考虑电动汽车充电站布局优化的配网规划模型，提出了一种新的辐射状约束保证可行解对应的规划方案均为辐射状网络。文献［6］提出了一种含电动汽车的新型直流配电网，提高分布式发电的利用率，并节省储能装置的投资。文献［7］为电动汽车用户设计了一种充放电策略，使用户在保证正常需求的情况下可以在低电价时段充电，高电价时段向电网售电。文献［8］对充换电和集中充电统一配送这两种换电模式的结构、运营流程进行了分析，提出分别以总充电费用最小和日负荷曲线波动最小为目标两阶段有序充电优化模型。文献［9］提出了电动汽车充电分时电价时段划分方法，并建立了以用户充电费用最小和电池起始充电时间最早为控制目标的数学模型。文献［10］利用分时电价机制引导和蒙特卡洛方法模拟不同管理模式下的EV负荷，采用场景生成和K均值聚类算法构造风光典型场景集，以年总经济成本最优为目标函数，经粒子群算法优化得出含EV的微电网容量配置方案。文献［11］重点介绍了V2G技术中电动汽车与电网互动双向电能检测系统的设计，并对双向电能检测系统进行软硬件的设计。

1 问题的描述

由于电动汽车隶属于用户的私人财产，用户的使用意愿具有随意性、不可控性，如果在调控过程中使用户的利益受损，电网将会失去与用户合作的机会。因此，电动汽车的充放电调度需要建立在用户满意度的前提下。本文首先考虑用户的利益与出行意愿，其次考虑电动汽车放电对电网的削峰影响。

1．1 目标函数的建立

式中P为30辆电动汽车在10个时刻内的总收益;q1(j)为在j时刻正在充电电动汽车的数量;q2(j)为在j时刻不充电也不放电电动汽车的数量;q3(j)为在j时刻正在放电的电动汽车的数量，其中q1(j)+q2(j)+q3(j)=30;k1为－1，代表电动汽车正在充电;k2为1，代表电动汽车正在放电;k3为0，代表电动汽车既不充电也不放电。

1．2 约束条件

(1)单个用户收益约束

P(i)≥0 (2)

为保障每个用户的利益，应当设置单个用户收益约束，使每个用户收益都处于不亏损状态，如若调控结束后P(i)＜0，则应给予用户响应补贴，直至P(i)=0。

(2)放电上限约束与充电下限约束

10%≤SOC(i)≤90% (3)

不管调控策略是否对电动汽车i进行放电，当SOC(i)≥90%时，都对电动汽车i进行放电操作。当电动汽车SOC(i)≤10%时，电动汽车电量不足，不管调控策略对电动汽车i如何调控，此时对电动汽车i进行充电操作。

(3)峰谷差值约束

式中ftop为j时刻之前的峰时负荷值;fvally为j时刻之前的谷时负荷值;Δf为峰谷差值上限，当峰谷差值低于此上限时，对剩余电量不足10%的电动汽车进行充电操作;当峰谷差值高于此上限时，按照粒子群算法对电动汽车进行充放电操作。

(4)满意度约束0≤S(i)≤Stop(6)在第二阶段调度中，当S(i)＞0时，用户处于满意状态，满意度值S(i)的增加速度会随着实际电量值增加而减慢;即当电动汽车电量满足用户所需电量时，用户会感到满意，但是在电动汽车电量满足用户所需电量的前提下，随着充电的进行，用户的满意度的增加速度远小于实际电量值的增加速度;这时为了给用户节约电费，应当设置满意度上限值Stop。

2 模型的建立

考虑用户的利益，建立基于粒子群算法的第一阶段模型与基于用户满意度的第二阶段模型。选取日间12个时刻对电动汽车进行充放电调控，设置前10个时刻为第一阶段，在第一阶段中首先利用粒子群算法确定各个时刻充电电动汽车与放电电动汽车的数量，再根据各个电动汽车的剩余电量与相应的约束条件，对具体哪几辆电动汽车充电，哪几辆电动汽车放电进行调控，目的在于在整个调控过程中使用户的利益得到最佳化;设置后两个时刻为第二阶段，在第二阶段中，根据第一阶段末尾电动汽车剩余电量与用户设置行程所需电量计算得出用户满意度值，继而根据满意度值对电动汽车进行调控，目的在于在整个调控过程结束后，在保障用户利益的基础上，使剩余电量能够满足用户的需求，如图1所示。

图1 电动汽车调控模型Fig．1 Electric vehicle control model

2．1 第一阶段模型

在第一阶段模型中，利用粒子群算法对充放电电动汽车数量确定下来;再根据电动汽车电量对具体电动汽车进行充放电操作;使用户的利益得到最佳化，并保障电动汽车电池不会过度放电。

2．1．1 粒子群算法

在粒子群算法中，对一群没有质量和体积的粒子进行初始化，每个粒子都是目标问题的潜在解向量，根据适用度函数算出每个粒子的适应值，再通过与个体极值、种群极值对比，逐渐向最优值靠拢，其中粒子利用式(7)更新速度，利用式(8)更新位置，经过若干次的迭代，得到最优解向量。图2为粒子群算法流程图。

V(i)=w×V(i)+c1×rand()×［pbest(i)－present(i)］+c2×rand()×［gbest(i)－present(i)］ (7)

present(i)=present(i)+V(i) (8)

图2 粒子群算法流程图Fig．2 Particle swarm algorithm flow chart

2．1．2 粒子群算法在电动汽车充放电调控上的应用

将粒子群算法应用到电动汽车调控第一阶段中，由于不同时刻的电价不同，可通过在不同时刻对电动汽车进行充放电操作，使用户的充电所交电费与放电所得电费得到最优化处理，同时为了保证在第二阶段用户的满意度，电动汽车电量在第一阶段中也不得低于一定的阈值。

图3为第一阶段电动汽车充放电调控模型，首先根据各时段电价，利用粒子群算法确定各个时段充放电的电动汽车数量。再根据电动汽车剩余SOC排序法，对电量剩余多的电动汽车进行放电，对电量剩余少的电动汽车进行充电。下一步进行判断，如果电动汽车SOC值大于90%则对电动汽车进行放电，如果电动汽车SOC值小于10%则对电动汽车进行充电。若当前时段峰谷差值小于Δf，则对电动汽车进行充电;若当前时段峰谷差值大于等于Δf，则利用电动汽车剩余SOC排序法对电动汽车进行充放电操作。

图3 第一阶段电动汽车充放电模型Fig．3 The first stage charge and discharge model of electric vehicle

2．2 第二阶段模型

在第二阶段模型(见图4)中，根据用户所设置的行驶里程，推算出用户所需电量，再结合当前实际电量算出满意度值，若满意度值小于零则对此电动汽车进行充电;若满意度值大于等于零，则说明电动汽车电量已满足用户需求，既不对此电动汽车进行充电也不对此电动汽车进行放电，等待用户使用。

图4 第二阶段电动汽车充放电模型Fig．4 The second stage charge and discharge model of electric vehicle

3 算例分析

3．1 参数的设置

为了验证二层优化模型对于提升用户利益的有效性以及提升用户满意度的有效性，以北京市某公司员工为例，在07:00～19:00时段对电动汽车充放电进行仿真计算。假设此公司有员工300名，平均每人有一辆汽车，则此公司汽车总数为300辆，其中电动汽车30辆，电动汽车普及率为10%。假设用户电动汽车充满电续航里程为200 km，则可根据式(9)计算得出电动汽车SOC值:

式中d需(i)为用户需求里程;d总为电池充满电状态下续航里程。

所提出的粒子群算法，以各时段用户利益之和作为适应度函数，通过对各个粒子适应度值的对比计算，得出最优解，继而得到在各个约束条件下用户的最优利益。其中参数c1=c2=1，进化次数n=200，种群规模s=200，假设每辆电动汽车充放电功率为2．5 kW，电动汽车充电每小时SOC值可增加10%，电动汽车放电每小时SOC值同样减少10%。

图5所示为电动汽车初始剩余电量，即电动汽车开始参与调控时的剩余电量;图6所示为用户需求里程，在第二阶段调控中，可根据用户需求里程与公式(9)计算出用户需求电量;图7为峰谷电价图，即各个时段的电价。

图5 电动汽车初始剩余电量Fig．5 Initial residual power of electric vehicle

图6 用户需求里程Fig．6 Requirements mileage of users

图7 各时段电价曲线Fig．7 Price curve for each period

3．2 算例结果

3．2．1 第一阶段调控算例分析

图8所示为第一阶段中各时段充放电电动汽车的数量，在7:00～9:00期间虽然处于低谷电价，但电动汽车电量都比较充足，此时放电电动汽车占据绝大多数;在10:00～12:00期间，此时处于峰时电价，电动汽车放电可以给电动汽车用户带来更多的收益，所以大多数电动汽车仍处于放电状态;在13:00～16:00期间，此时电价波动比较剧烈(即13:00～14:00为平时电价，15:00为谷时电价，16:00为峰时电价)，而此时电动汽车经过前几个时段的放电，剩余电量也相应处于较低状态，因此可以看出，在13:00～16:00时段内，充电电动汽车数量明显增长。

图8 第一阶段控制中充放电电动汽车数量Fig．8 Number of charge-discharge electric vehicle in the first stage

图9 所示为用户第一阶段控制中负荷曲线图，实线为调控前负荷曲线，虚线为基于粒子群算法的电动汽车调控策略的负荷曲线，在7:00～10:00，13:00～16:00期间，负荷值都在原有负荷曲线的基础上略有下降;在10:00～13:00期间，负荷值在原有负荷曲线的基础上有大幅下降;在可以看出在各个时刻负荷值都有所减少，尤其是在峰值时刻，负荷值减少最为明显，说明此调控策略在保证用户利益的基础上还起到了削峰的作用。

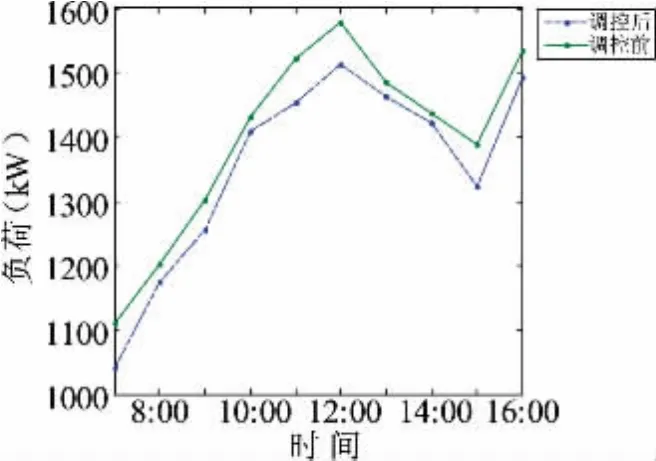
图9 第一阶段控制中负荷曲线图Fig．9 Load curve in the first stage

图10 所示为用户利益曲线，在粒子群算法中随着迭代次数的增长，各粒子都会不断向最优值靠近。如图所示当迭代次数为120次左右时，用户利益达到最优为159元。

图10 用户利益曲线Fig．10 Interest curve of users

图11 所示为第一阶段调控后各个电动汽车剩余电量，为避免过度放电导致的电量过低，电动汽车在第一阶段调控结束后剩余电量应保持在10%以上，图11所示的电动汽车全部满足要求。

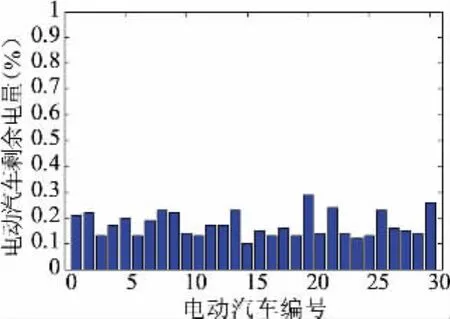
图11 第一阶段结束后电动汽车剩余电量Fig．11 Electric car remaining power after the first stage

3．2．2 第二阶段调控算例分析

图12为第二阶段调控后各电动汽车的剩余电量。在经过第二阶段调控后，各电动汽车剩余电量与第一阶段结束时相比都有一定的提升，剩余SOC值基本保持在20%～50%之间。由于用户需求电量的差异，导致第二阶段充放电调控具有差异性，当电动汽车剩余电量满足用户需求电量后，电动汽车就不再充电，同时等待用户使用;当电动汽车剩余电量不满足用户需求时，电动汽车就会持续充电。

图12 第二阶段调控结束电动汽车剩余电量Fig．12 Electric car remaining power after the second stage

图13 所示为第二阶段调控结束后用户满意度值。当用户满意度值大于0时，代表用户处于满意状态，电动汽车剩余电量满足用户需求;当用户满意度值小于0时，则相反。如图13所示，其中处于满意状态的用户数有27户，处于不满意状态的用户有3户，用户满意率为90%。由此可以看出第二阶段调控可以基本满足用户的电量需求。

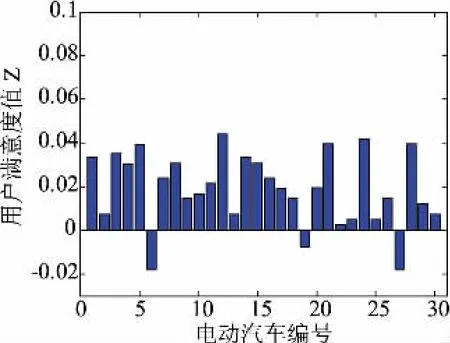
图13 第二阶段调控结束后用户满意度值Fig．13 User satisfaction value after the second stage

图14 所示为电动汽车用户在参与第一阶段、第二阶段调控后的收益与花费情况，可以看出每个用户都可以通过日间放电获得一定的收益，但用户都要在第二阶段调控中花费少量电费来补充电量，通过第一阶段与第二阶段调控每位用户都至少达到不亏损状态(即总收益为0);这是由于用户的收益与电动汽车的起始电量有很大关系，当电动汽车起始电量较少时，在峰值电价时电动汽车就不能通过放电来获得收益;在理想状态下(即每辆电动汽车的起始电量都在一定的阈值之上)，每位用户都可以通过对电网反向供电获得一定的可观收益。