一类分数阶微分方程组无穷点边值问题正解的存在性

陆心怡

（池州学院数学与计算机学院，安徽池州247000）

1 引言

近年来，分数阶积分以及分数阶微分方程理论越来越多的运用在各个领域,在流体力学、化学、工程学、生命科学等方向有着广泛且重要的应用，作为非线性分析的一个重要分支，很多学者也非常热衷于研究分数阶微分方程正解的存在性和唯一性以及变化的多样性.且经过实际检验,相对来说分数阶模型比整数阶模型应用的领域可能更加宽泛和精确[1]，对于研究结果的准确性有着很大影响.

本文用Leray-Schauder非线性抉择性来研究下面的分数阶微分方程组无穷点的边值问题：

n-1＜α,β≤n,i为固定常数，i∈N,i≤n-2,α,β≥2.是连续函数,是黎曼刘维尔形式的,其中

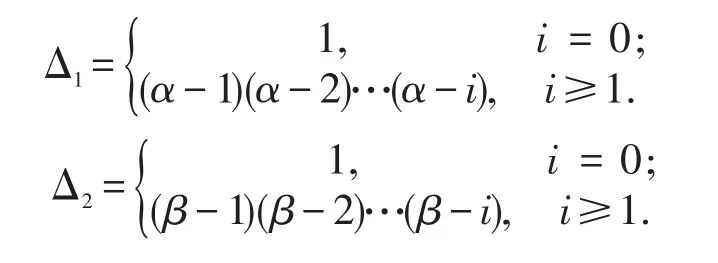
2 预备知识和引理

首先给出相关的定义、引理以及定理等.

定义1[2]函数的 i∈N,i≤n-2,α≥2,阶Riemann-Liouville积分定义如下

0＜t＜1,n-1＜α≤n,，

其中右边是在ηj≥0上逐点定义的.

定义2[2]函数的0＜ξ1＜ξ2＜…＜ξm-2＜1,阶Riemann-Liouville微分定义如下

引理1[3]设 α＞0,假设u∈C(0,1)⋂L(0,1),那么微分方程有唯一解其中 n 是不小于 α的最小整数.

引理2[3]对于一个α(α＞0)阶分数阶微分,给出那么

其中n为不小于α的最小整数.

注[2]α(α＞0)阶的Riemann-Liouville微分和积分有以下性质：α,β＞0,u∈L(0,1).

引理3设 f∈C[0,1],n-1＜α≤n,i为固定常数,i∈N,i≤n-2,α≥2.那么微分方程

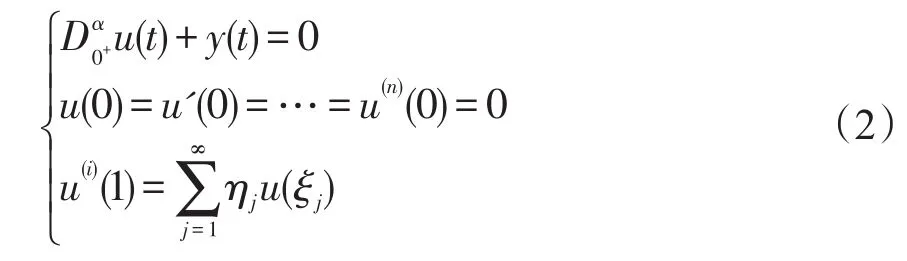
有唯一解

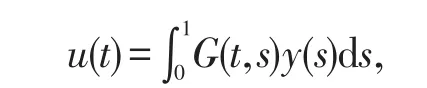
其中

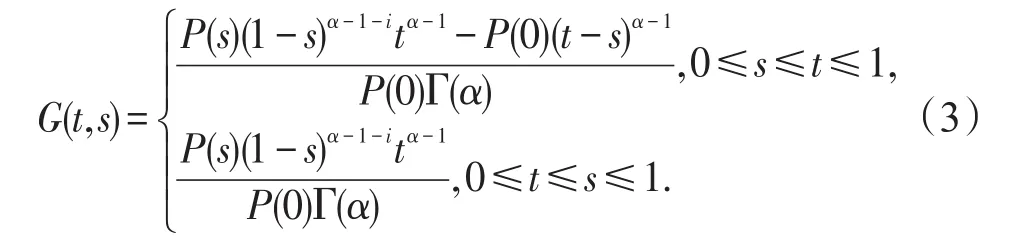
证根据引理1,首先，将(2)中的微分方程转化成与之等价的积分方程

由u(0)=u'(0)=...=u(n-2)(0)=0,得c2=c3=…=cn=0.即

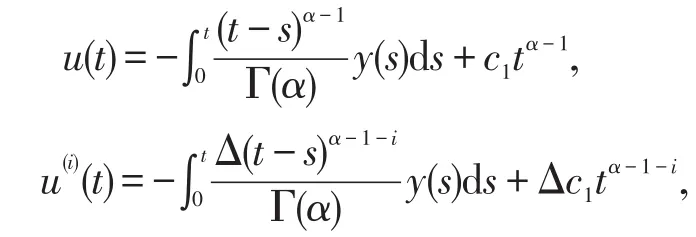
那么

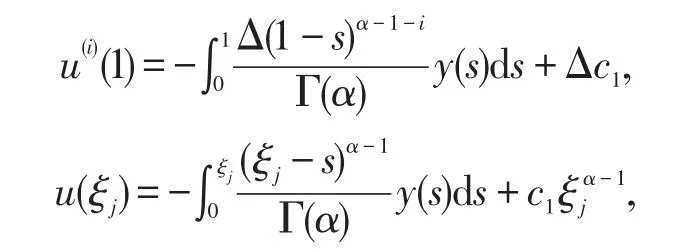
因此,

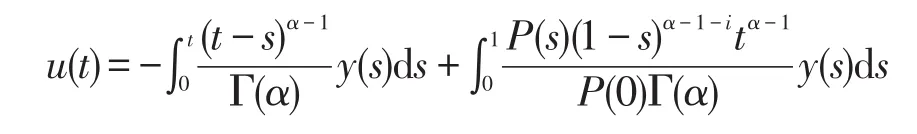
则微分方程（2）的唯一解是

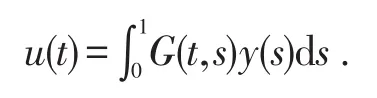
得证.

引理4P(0)＞0,P(s)满足以下两个条件：

a.P(s)在[0,1]上单调增且恒成立;

b.存 在 M1≥m1≥0 使 得 任 意有m1s+P(0)≤P(s)≤ M1s+P(0).

证a容易算出 P'(s)≥0,因此P(s)单调增,又P(0)＞0,知 P(s)≥P(0)＞0;

并且 M1≥m1≥0,且m1s≤P(s)-P(0)≤M1s,∀s∈[0,1].

引理5由（3）定义的函数G(t,s)具有以下性质：

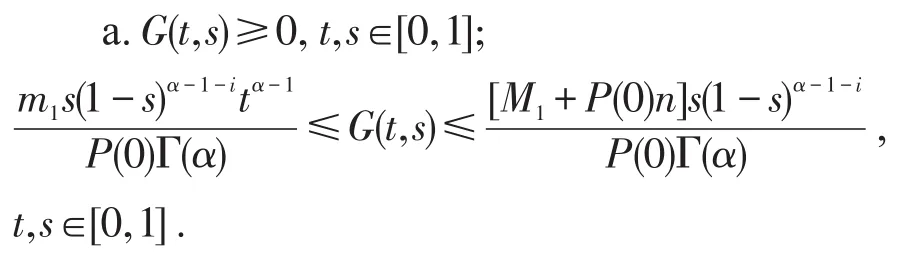
证明略[1].

引理6[4](抉择性)E是Banach空间,C是E中的凸闭集.假设U是C的相对开子集,0∈U且是连续开子集.则下列条件：

a.A在U中有一个不动点;或者

b.存在u∈∂U,λ∈(0,1)使得u=λAu;

成立。

3 主要结果

引理7[1]设是连续函数,且满足假 设 存 在0＜σ＜1使得 tσF(t)在 [0,1]上是连续函数.那么是连续函数.

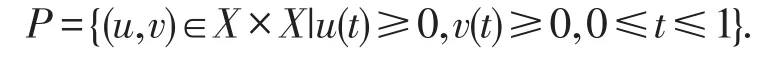
那么方程组（1）可以转化成下面的方程：

该部分的证明可由[5]中的引理3.3得出.下面来定义一个算子A:X×X→X×X

引理 8[1]令 n-1＜α,β≤n,i为固定常数,i∈N,是连续函数并且满足假设存在 0＜σ1＜1使 得在 [0,1]×[0,+∞)是 连 续 函 数,则A:P→P是全连续算子.

（2）存在r＞0,有

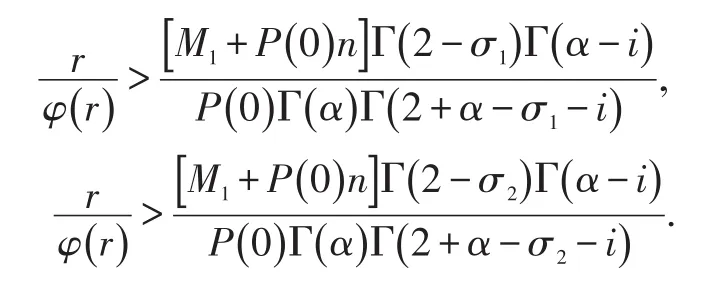
那么方程组（1）存在一个正解.

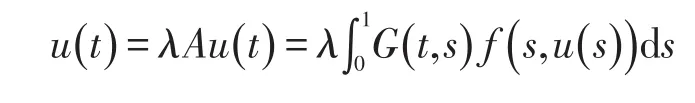
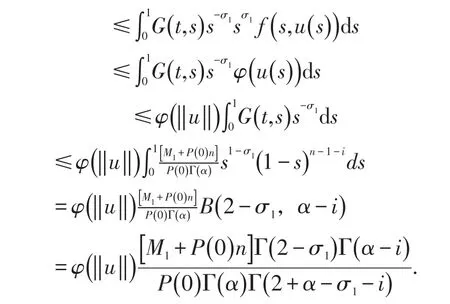
所以,

综上所述,由引理6可知存在不动点u∈Uˉ,v∈Uˉ因此方程组（1）存在一个正解.