基于改进遗传算法的限容量多旅行商问题研究

束东来，张玉州

（安庆师范大学 计算机与信息学院，安徽安庆246133）

限容量多旅行商问题（LCMTSP）是对经典旅行商问题（TSP）及多旅行商问题（MTSP）的模型扩展。

实际问题中让一个人从一个城市出发去拜访若干个城市，其工作量是巨大的，所以考虑到工作效率等问题，MTSP更符合实际，而每个旅行商的精力是有限的，安排一个合理访问城市个数的范围是有必要的[2]，LCMTSP问题在MTSP问题基础上，给每个旅行商施加了一个访问城市个数的限制条件，显然更符合实际意义。

本文以3个旅行商、每个旅行商访问城市不少于3个但不多于10个、从一个城市出发访问其余19个城市并回到出发城市问题为例，对传统的遗传算子稍加改进，实验证明能够较好的解决限容量多旅行商问题。

1 LCMTSP数学模型

带有容量限制的多旅行问题是在原有的多旅行商问题的基础上多了一个容量限制的约束条件。其目标函数为m个旅行商所走的路程最短，其约束条件为m个旅行商中每个旅行商访问城市的个数有上下限。

本文模型与基本TSP问题一样，是寻找加权图中最短回路问题[4]，假设城市号从1～n，其中城市1为出发城市，m个旅行商。

定义变量：

其中i=1,2...N，k=1,2...M

目标函数为：

约束条件：

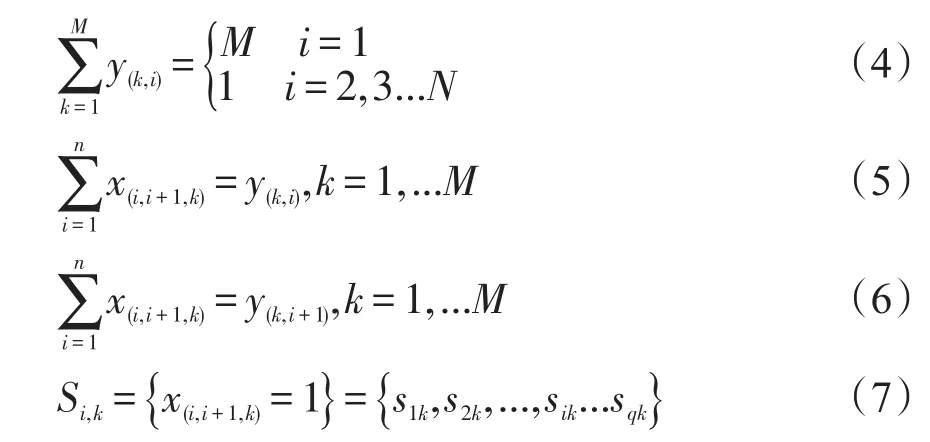
其中Si,k为第k个人访问的城市的合集，sik代表第k个人访问的第i个城市，q代表访问者访问的城市数目

公式（4）代表从指定城市1出发，所有城市仅有1个访问者严格访问一次；

公式（5）表示任意一条路线的次终点城市（iq,k）仅有一个起始点城市与之相连；

公式（6）表示任意一条路线的起始点城市仅有一个次终点城市（iq,k）与之相连；

公式（7）表示第k个访问者访问的所有城市；

公式（8）表示所有访问者访问的城市总和；

公式（9）每个访问者最少访问a个城市，最多访问b个城市；根据本文20个城市、3个旅行商、每个旅行商访问城市个数不少于3个且不多于10，约束条件（9）改为3≤q≤10。

2 遗传算法设计

2.1 编码

本文采用以遍历城市的次序排列的一种染色体自然编码方法，即一个解序列表示一条染色体。如串码0-1-2-3-4-5-6-7-8-9-0表示自城市0开始，依次经1，2，3，4，5，6，7，8，9，遍历路径，最后返回城市0[5]。

如城市为0，1，2，...，19的三个旅行商问题的一条染色体编码为：

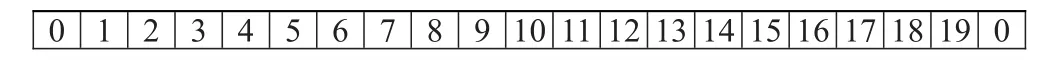
其中断点分割随机断点r1、r2；如r1=6，r2=12：

将断点r1、r2插入染色体编码中，断点的选择会受到问题容量限制条件的约束，每个旅行商访问城市个数为不少于3个且不多于10个。

则三个旅行商的路径分别表示为：

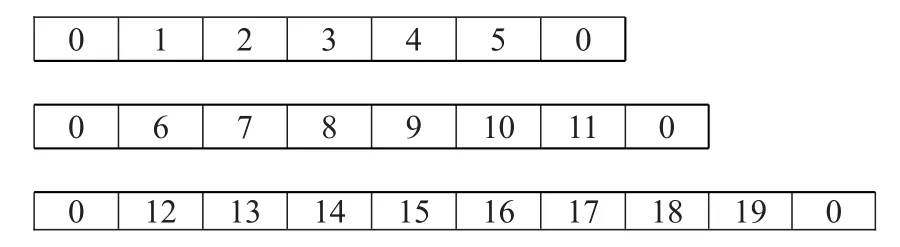
2.2 群体规模

合理的群体规模对遗传算法的收敛具有重要意义[6]，群体规模太小难以得到满意的结果，群体规模太大会使计算复杂。根据经验，本文群体规模取100。

2.3 适应度函数

适应度函数是根据个体的适应值对其优劣判定的评价函数。在旅行商问题中用访问路径的总距离的倒数作为适应度函数来评价求解结果是否最优[7]。即：

2.4 初始化种群及初始化父代

2.4.1 种群初始化 产生一个sizepop×19的数组，每一行存储一个序列；产生随机断点，存储在sizepop×2的数组；把对应的断点加入初始化数组中，求出sizepop×19个体中最优的记录对应序列反下标。2.4.2初始化父代 初始化父代采用完全随机（inti_rand_nerb）与次优选择(init sub sele)相结合的方法。产生一个随机数，如果生成的随机数是0，就采用完全随机的方式一个父代；如果生成的随机数是1，就采用最近邻法生成一个父代。

在完全随机方法中，首先产生一个1～19的一个随机数作为序列的第一个元素，然后依次循环产生此序列的下一个元素，在每次产生下一个元素的时候判断是否与此序列中前面产生的元素相等，若相等则重新产生，否则添加到序列中；然后再进行断点分割，分成三个旅行商的访问路径。

图1 完全随机法初始化父代

在次化选择法中，首先产生三个0～2的随机数，看作对应的旅行商，若当前产生的随机数为0，则在候选集合中选取距离第一个旅行商次近的城市，并添至其路径中，直到候选序列为空。例如下图2：

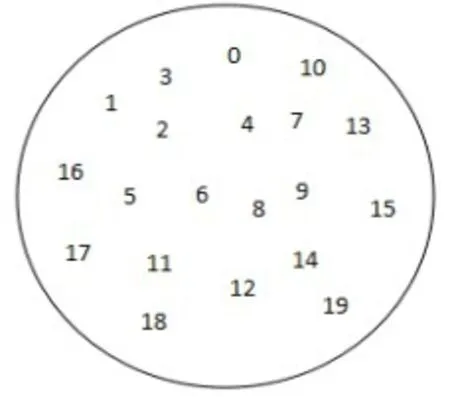
图2 次优选择法初始化父代

0为起始城市；

1,2,3 ,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19为需要访问的城市；

三个旅行商分别为T1、T2、T3；

产生一个0～2的随机数r；

计：r=0，选择未被选择的城市中距离T1所在位置次近的城市；

计：r=1，选择未被选择的城市中距离T2所在位置次近的城市；

计：r=2，选择未被选择的城市中距离T3所在位置次近的城市。

2.5 控制容量操作

根据本文容量限制这一约束条件，控制每个旅行商访问城市个数范围：3≤q≤10；产生一个length×19的旅行商，随机产生一个3～10之间的随机数，作为第一个断点；再产生另外一个随机数，使得与前面产生的随机数的距离大于3且与终点的距离大于3且不大于10，作为另一个断点。

2.6 选择操作

在群体大小为n的群体中，如果一个个体i的适应度为fi，则该个体被选择的概率，然后对各个染色体计算它们的累积概率，概率Pi表示个体i的适应度在群体的个体适应度总和所占的比例，个体适应度大的被选择的概率就越高[9]。

运用轮盘赌法选择较优个体，为了选择父代需要进行多次选择，每次产生一个[0,1]的均匀随机数，将该随机数作为选择指针来确定备选父代个体。

2.7 交叉操作

交叉算子是遗传算法里面的核心算子。交叉算子里面的交叉概率的设置较为重要，交叉概率大能增强遗传算法开拓新搜索空间的能力，但有可能会破坏一些性能较好的基因串，而交叉概率小又会引起算法迟钝。本文交叉概率取0.8。

对于LCMTSP问题，本文交叉算子采用PMX算子、OX算子、CX算子以及最小路径交叉规则等算子与断点分割过程相结合。

部分匹配交叉算子（Partially Matched Crossover，PMX）是针对TSP问题提出的基于路径表示的交叉操作，先均匀随机分布两个交叉点，定义这两个点之间的区域为匹配交叉区域，使用位置交换操作将两个父代该区域进行交换，交换出现重复的部分用原基因位的数字代替[10]。

顺序交叉算子（Ordered Crossover，OX）是针对TSP问题提出的基于路径表示的交叉操作，该算子能够保留排列并融合不同排列的有序结构单元[11]。两个父代交叉时，选择其中一个父代的一部分，保存另一个父代中代码的相对顺序生成子个体。

循环交叉算子（Cycle Crossover，CX）也是针对TSP问题提出的[12]，循环交叉操作中子代的代码顺序根据其任意父代个体产生。

最小路径交叉规则(Minimam Puth Crossover,MPC)是本文在三个旅行商之间操作的一种交叉算子，根据断点分割后的三个旅行商，用产生的随机数对其中两个旅行商进行交叉互换操作。例如：

一条父代的染色体编码为：

产生两个随机数r1、r2∈（0,2），如r1=0、r2=1就旅行商A与旅行商B进行交叉；计算旅行商A与旅行商B中旅行商访问城市少的城市个数，如上所示，旅行商A访问城市个数为6，旅行商B访问城市个数为9，选择L=6（L为需交叉的路径长度）；产生两个随机数q1、q2∈（1，6），如q1=2，q2=5，对旅行商A、B进行交叉互换：

2.8 变异操作

变异算子在遗传算法中属于局部搜索操作，其目的是维持种群的多样性。变异算子里的变异概率也较为重要，较低的变异概率能防止种群中优良基因的丢失，但是降低了遗传算法开拓新搜索空间的能力[13]，而较高的变异概率又会降低算法的收敛度和稳定性。本文变异概率取0.01。

对于LCMTSP问题，本文变异算子采用SWAP算子、2-opt算子、3-opt算子以及SI、DI算子与断点分割过程相结合。

SWAP算子是两点对换算子，将位置r1，r2，将这两个位置的数字进行对换。

2-opt算子是为了加速进化而加入的一个操作，具有单向性，即只有逆转之后个体变得更优才会执行2-opt操作，否则逆转无效[14]。根据小路径取反原则，产生[1,19]之间的两个位置r1、r2，将r1和r2之间的基因序列进行反向排序。

3-opt算子是在2-opt算子的基础上又选了一个逆转点，产生[1,19]之间的三个位置r1、r2、r3，将离第一个城市最近的位置点与第一个城市位置点之间的序列进行反向排序，将后两个位置点之间的基因序列进行反向排序。

SI算子是一种单插入变异算子，将路径中一个位置r1的数删除，插入该路径的另一个位置r2前面。例如：

一条父代的染色体编码为：

DI算子是一种双插入变异算子，它将路径中连续两个位置r1、r2从当前位置删除，插入该路径的另一个位置r3前面。例如：

一条父代的染色体编码为：

本文考虑到所有位置变异情况，即上述5种变异算子中每一个点都要进行测试，即遍历所有可能的情况，选择最优的过程，算改变后的总距离，然后选取最优的解（总距离最短），遗传到下一代。

3 实验结果及分析

本文借助 C 语言，在 Intel（R）Core（TM）i5-6500 CPU处理器计算机环境中对LCMTSP问题的遗传算法进行研究，用3个旅行商访问20个城市的LCMTSP实例进行测试，选取100个染色体作为初始种群，最大遗传代数为1000，交叉概率为0.8，变异概率为0.01。

实验对程序进行了运行10次、20次、50次、100次，将本文提出的模型与原始MTSP模型进行对比，并对实验结果进行分析，取实验结果的平均值及最小值的方法来提高实验的准确性和可信度。

实验对LCMTSP问题进化代数100、300、600、1000、1500代进行了实验，取实验结果的平均值及最小值的方法来提高实验的准确性和可信度。

实验结果如表1和表2所示：

表1 LCMTSP与原始MTSP实验对比

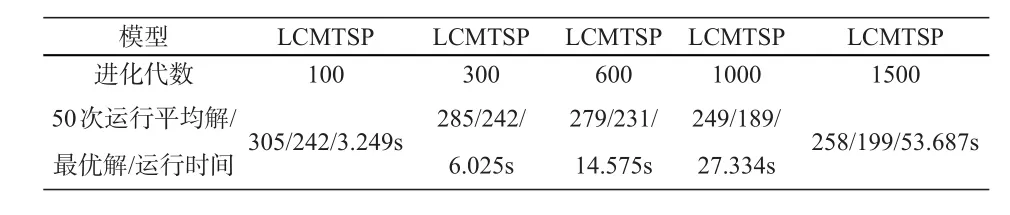
表2 gen=100、300、600、1000、1500代时的解、运行时间

借助Matlab2014a软件，程序运行一次，LCMTSP模型进化轨迹图如图3-图8所示：

图3 种群初始化

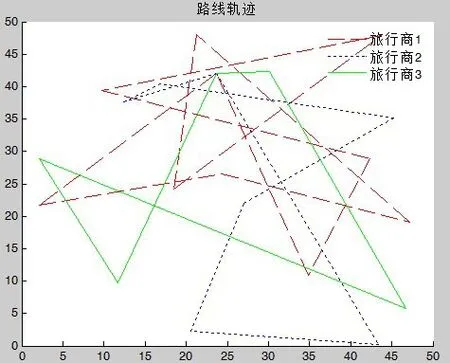
图5 gen=300，l=341.893153

图6 gen=600，l=289.967866

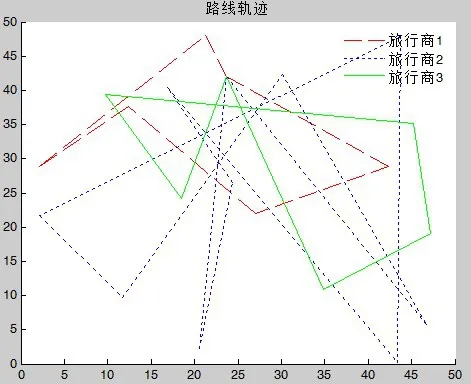
图7 gen=1000，l=250.927191

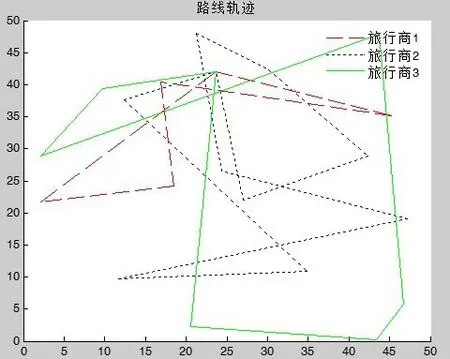
图8 gen=1500，l=279.258567

从程序运行结果可以知道，由于遗传算法是一种启发式算法的特性，每次运行的结果大都不相同但都相近。

从实验结果最优解与平均解可以看出本文限容量多旅行商问题与传统多旅行商问题实验结果总距离差距不大甚至更优。

从实验运行时间来看，本文模型运行时间比传统多旅行商问题运行时间稍短。

从实验对LCMTSP问题进化代数来看，在进化到1000代左右时，总距离基本已经可以达到最小值，再进化更多代数总距离无明显改进。

综合实验结果与实际意义，本文提出的限容量多旅行商问题模型比传统多旅行商问题更具有实践意义与价值。