永磁同步电机新型变结构直接转矩控制

任凤娟

0 引言

随着永磁材料技术的不断发展和进步，永磁同步电机(permanent magnet synchronous motor，PMSM)由于其具备多种独特的优势而被广泛应用于各种场合[1-5]。目前，对于PMSM控制而言，仍然采用比较成熟的矢量控制策略，且通常要准确地知道被控交流电机的参数。随着电机控制技术的发展，相比于矢量控制，直接转矩控制（Direct Torque Control，DTC）的出现在一定程度上解决了传统矢量控制所存在的缺点[6-8]。然而，传统的DTC技术存在低速时转矩脉动大的问题。为了解决这个问题，近些年来提出了许多新型的直接转矩控制系统，但大部分算法都是用在静止坐标系下[5-7]，而对旋转坐标系下的DTC研究较少。本文设计了一种基于新型直接转矩控制的PMSM控制系统，利用滑模变结构控制强鲁棒性特点，将变结构控制与直接转矩控制相结合，设计了一种旋转坐标系下PMSM变结构直接转矩控制系统。最后通过仿真验证了该算法具有较好的动静态性能。

1 永磁同步电机的数学模型

为了便于控制器的设计，首先给出d-q坐标系下PMSM的数学模型为[9-13]：

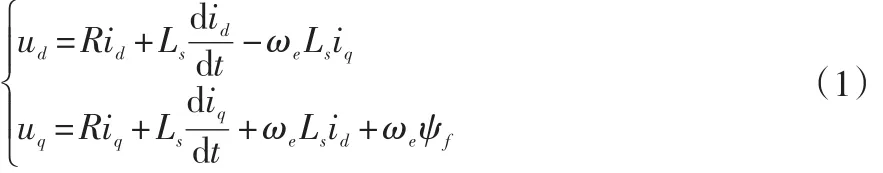
其中，udq，idq分别为d-q轴的定子电压和定子电流；Ls为定子电感；R为定子电阻；ψf为永磁体磁链；ωe为电机的电角速度。

为了便于控制器的设计，本节介绍一种同步旋转坐标系d-q下的矢量数学模型，表贴式PMSM的数学模型表达式可表示为：

此时，电磁转矩Te的表达式为：

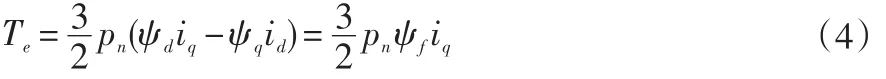
其中，pn为电机的极对数。

2 变结构直接转矩控制器设计

2.1 二阶滑模变结构控制的基本原理

为了不失一般性，考虑单输入单输出非线性系统：

其中，x∈Rn为系统的状态变量，u∈R为系统的控制量，h为输出函数，称为滑模变量。 f、g为光滑的不确定函数。假设系统(6)的相关度为2，则对h(x)进行连续求导有：

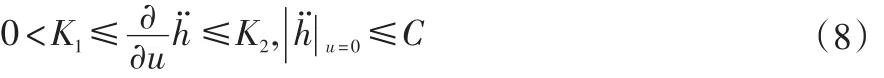
成立。则局部坐标[ξ1ξ2]T=[h ḣ]T，可以将二阶滑模控制问题等效为有限时间稳定问题[8]：

根据滑模控制的原理，就是要设计一个滑模控制器，使滑模变量在有限时间内收敛为零。在二阶滑模控制器设计中，采用螺旋算法[14-15]来设计控制器为：

若滑模变量h的一阶导数的上届已知，即：

则kp,ki的值可以通过下式进行调整：

2.2 变结构直接转矩控制器设计

传统DTC中的磁链控制器和转矩控制器通常分别采用滞环调节器，这将会引起转矩脉动问题。为了改善传统DTC的控制性能，本节将设计一种基于螺旋算法的变结构直接转矩控制器，具体设计如下。

首先，为了获得磁链控制器的表达式，定义磁链的滑模面函数：

利用基于螺旋算法的二阶滑摸控制基本原理，此时磁链控制器的表达式为：

其中，kp,ki＞0为待设计参数。

假设定子磁链ψr的幅值为一常数，此时电磁转矩Te的微分方程可表示为：

为了获得转矩控制器的表达式，定义转矩的滑模面函数

同样利用基于螺旋算法的二阶滑模控制基本原理，此时转矩控制器的表达式为：

此时，基于螺旋算法的变结构DTC的实现框图如图1所示，此方法是基于旋转坐标系下的控制算法。

图1 变结构直接转矩控制的控制框图

3 仿真与实验验证

采用如图2所示的PMSM调速控制系统进行仿真及实验验证。从图中可以看出，该控制策略主要包括以下几个部分：转速环调节器、磁链和转矩调节器、磁链和转矩的计算和SVPWM算法等。

3.1 仿真结果分析

为了验证文中所提控制算法的正确性，根据图2所示的控制框图搭建系统的仿真模型。电机的参数设置为：定子电感Ls=8.5 mH，定子电阻R=1.2Ω，磁链ψf=0.175 Wb，转动惯量 J=0.000 8 kg·m2，极对数pn=4。其中，仿真条件设置为：参考转速为600 r/min，当t=0.5 s时突加负载转矩TL=1.5 N·m。

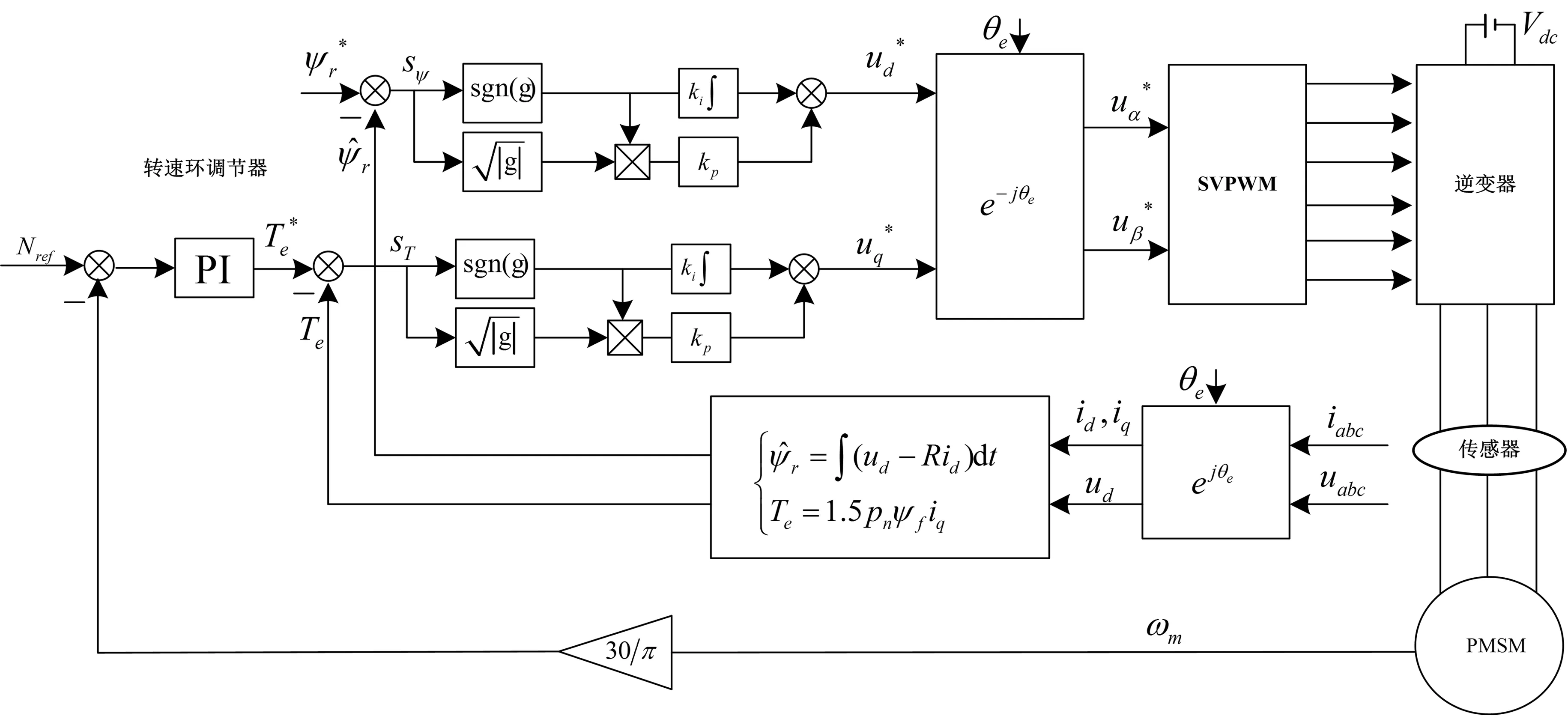
图2 基于螺旋算法的PMSM变结构直接转矩控制框图

为了便于比较分析，仿真中分别对传统DTC控制和文中所提的控制策略进行仿真比较，仿真结果分别如图3和图4所示。

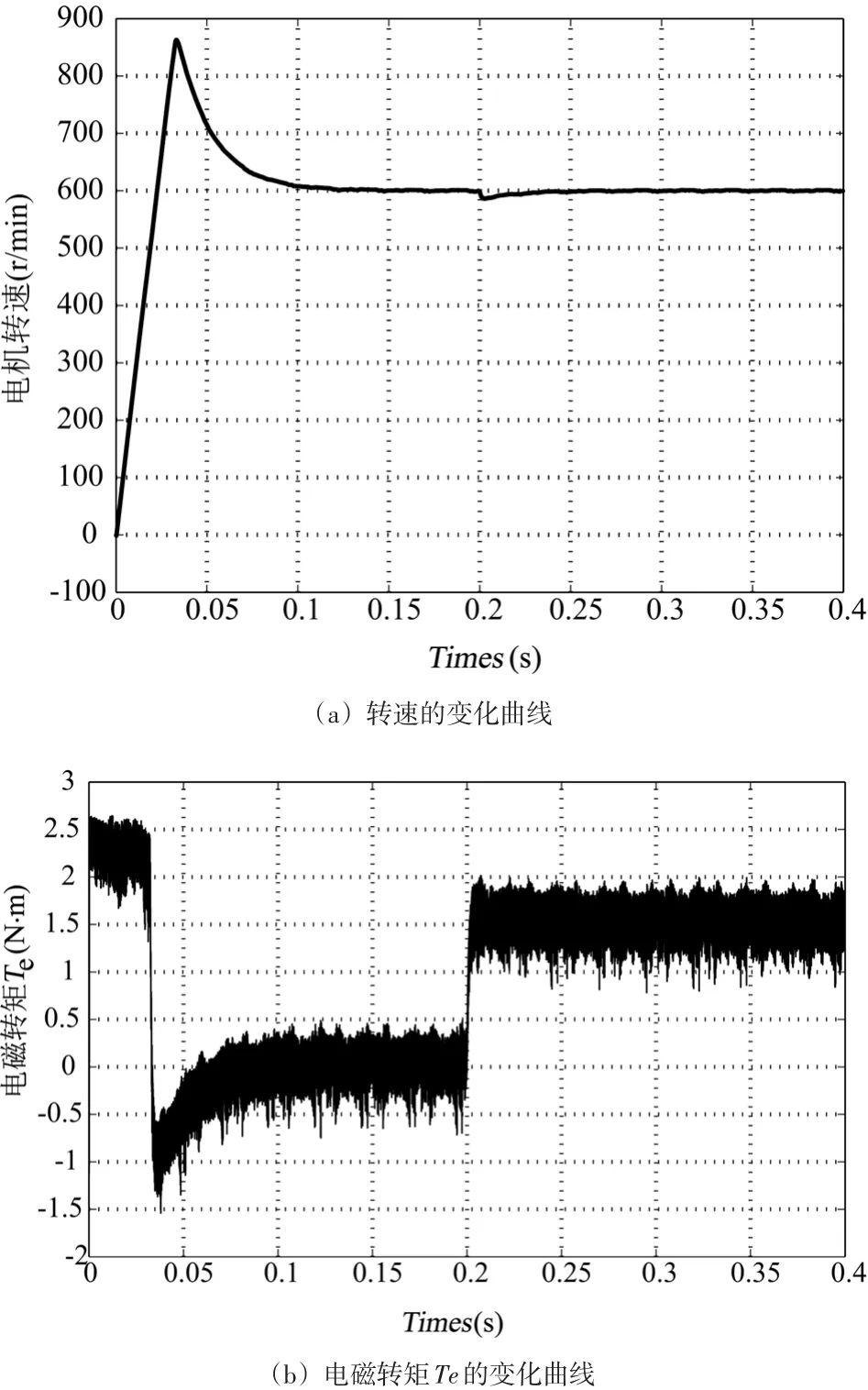
图3 基于传统DTC的仿真结果

从如图3(a)和4(a)可以看出，采用传统DTC时，电机空载启动过程中转速不仅有一定的超调，调节时间较长，约为0.1s；采用文中所提算法时，电机转速虽然有一定的超调量，但调节时间非常短，不到传统DTC控制的一半。另外，当电机突加负载时，文中所提控制算法具有较快的动态响应速度，且电机转速波动也很小，从而说明所提控制算法具有较好的动静态性能和鲁棒性。

图3(b)和4(b)给出了两种算法下电磁转矩的变化曲线对比，从图中可以发现，文中所提控制算法的转矩脉动非常小。另外，图3(c)和4(c)给出了两种控制算法下磁链估计值的变化曲线对比，同样可以发现，文中所提控制算法具有较快的动态响应速度。

从以上仿真结果可以看出，文中所提控制算法仍保持传统DTC控制固有的转矩快速响应的特征和对系统参数摄动、外干扰、测量误差以及测量噪声具有鲁棒性强的优点，且转矩脉动比较小，有效地改善了系统的动、静态运行性能。

图4 基于变结构DTC的仿真结果

4 结语

为了提高PMSM调速系统的动态性能，本文提出了一种旋转坐标系下PMSM变结构直接转矩控制。文中首先给出了旋转坐标系下PMSM矢量数学模型，其次将二阶滑模控制和直接转矩控制相结合，基于螺旋算法设计了一种变结构直接转矩控制。最后与传统DTC控制进行充分比较分析，验证了所提控制算法具有较好的控制性能，且算法简单，便于实现。