五轴联动机床旋转中心偏移补偿算法研究

庄瑛，周奎



五轴联动机床旋转中心偏移补偿算法研究

庄瑛1，周奎2

（1.四川省机械研究设计院，四川 成都 610063；2.四川工程职业技术学院，四川 德阳 618000）

五轴联动数控加工过程中，MCS是机床运动的依据，也是指令刀位点移动的依据。程序中刀位点的指令位置P＝P'＋ΔP；P'为基础分量，按转轴的旋转中心O与MCS的坐标原点O重合给出；另一分量ΔP是由于事实上的O与O的不重合而导致假定位置与程序中刀位点的指令位置存在着差异而需要的补偿量，它与O在MCS的位置相关。研究了O与O不重合刀位点指令位置补偿量的计算公式，开发了能自动生成带有旋转中心偏移自动补偿功能的数控加工程序的后置处理程序，适用于数控系统不具有RTCP功能及旋转中心偏移自动补偿功能的五轴加工程序编制。

五轴联动；数控加工；坐标变换；旋转中心；偏移；补偿；算法

五轴机床数控加工过程中，旋转轴在机床中存在着固定的位置和姿态，但其在设定MCS（Machining Coordinate System，加工坐标系）中的位置和姿态却必须要在MCS设定后方能最终确定。静态MCS作为机床运动的依据，也是指令刀位点移动的依据。刀位点是相对于刀尖点的某一固定位置，它由操作人员指定，一经指定，便成为了系统控制的对象。离线编程因不能确切知道转轴物理旋转中心O在MCS中的具体位置而时常假定为（0, 0, 0），即：假定MCS的坐标原点O或刀具的刀尖点与机床转轴的物理旋转中心O重合而在程序中指令理想刀位点P'位置。由于事实上的O或刀尖点与O的不重合而导致实际加工程序中的刀位点P与P'之间存在着位置差异ΔP需要补偿[1]。相当一部分高端数控系统已经开发了相应的自动位置补偿功能，而一些低端、老旧数控系统尚不具备此项自动补偿功能，须要结合O在MCS中的位置或O相对于刀尖点的具体位置而在实际加工程序中指令刀位点的准确位置。

1 旋转中心偏移补偿算法

1.1 工件旋转或摆动中心偏移补偿

图1为某T－T五轴机床（工作台双摆）加工过程中WCS（Workpiece Coordinate System，工件坐标系，自动编程前置处理理想刀位点位置的参照系）中某点P（X,Y, Z）顺序绕工作台的物理转轴Z、X转动和角度后，坐标变换到MCS中的详细情况，其中物理转轴Z、X在MCS的位置和姿态由矩阵决定：

此种类型的五轴机床加工过程中，刀尖点作为刀位点接受系统控制，MCS由机床参数设定时，对应各坐标轴与机床坐标轴平行且正方向一致。工件装夹时，保证WCS初始位置与MCS完全重合，即对应各轴平行（Xw//Xm, Yw// Ym, Zw//Zm）正方向一致且原点重合。WCS中的点Pw（Xw, Yw, Zw）顺序绕Zr轴旋转C角度、绕Xr轴旋转A角度后，坐标变换到MCS中的位置Pm（Xm, Ym, Zm）由式（2）、式（3）计算得到[2]，该点就是实际加工程序中指令刀位点的准确位置。Pm'为Or位置偏移量为（0, 0, 0）时，指令的理论刀位点位置如（4）所示：ΔPm为Or在MCS中偏移量为（Δx, Δy, Δz）时，实际加工程序中刀位点的指令位置与理想刀位点位置间的事实补偿量，如式（5）所示。

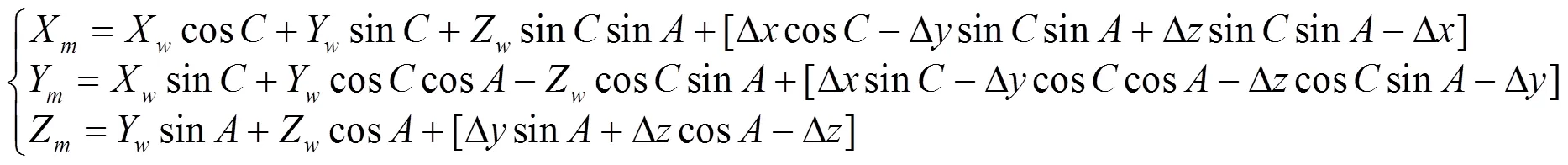
由此，实际加工程序中指令的刀位点的确切位置应为P＝P'＋ΔP，如式（6）所示。

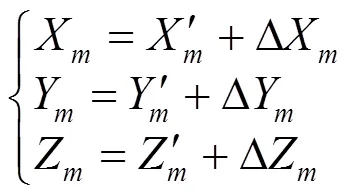
1.2 刀轴摆动中心偏移补偿

图2所示为H－H型五轴机床（主轴头双摆）刀位点相对于刀尖点的位置补偿算法全过程，X、Z为刀具的物理转轴和，摆动中心O作为刀位点接受机床数控系统控制，O相对于刀尖点的初始位置为（Δ, Δ, Δ）。数控加工过程中保证WCS与MCS对应各轴平行（X//X,Y//Y,Z//Z）方向一致，原点重合，姿态与位置保持固定不变。如T－T五轴机床一样，这类机床数控加工离线编程时，由于并不清楚刀位点相对于刀尖点的初始准确位置而假定为（0, 0, 0）。理想刀位点在MCS中的位置P'（X',Y',Z'）可直接由WCS唯一确定，即：P'＝P（X'＝X,Y'＝Y,Z'＝Z）。由于刀尖点与刀位点的位置不重合以及刀具摆动，摆动中心O（刀位点）相对于刀尖点的位置进一步改变而需要准确补偿。位置补偿量ΔP由式（7）、式（8）获取[3]。

图2 H－H型机床刀位点的位置补偿

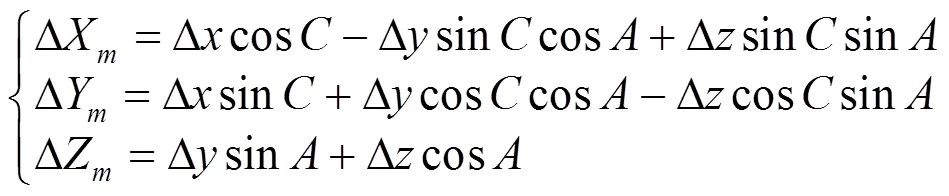
实际数控加工程序中指令的刀位点位置为P＝P'＋ΔP，即：

特殊情况下，刀具摆长为＝Δ、Δ＝0、Δ＝0时，刀位点的位置补偿计算公式为[4]：

2 旋转中心偏移补偿算法的实现

图3中，刀具的摆动及主轴带动工件的旋转分别为其物理转轴B、C，系统为SINUMERIK 840C，由于年代久远，系统老旧，不具有RTCP（Real-time tool center point rotation）功能及旋转中心偏移自动补偿功能，刀具的摆动中心常作为刀位点接受机床数控系统控制，程序的编制极为困难，重复利用率低，细微的参数调整，都需要重新编制加工程序。笔者结合机床的结构特点和补偿量的相应算法，设计了可编制旋转中心偏移自动补偿的数控加工程序，使编程变得简单，大大提高了程序的重复利用率。

图3 奥地利WFL M120 MILLTURN车铣复合加工中心

补偿量可按如下步骤实现：

（1）获取五轴联动数控机床结构信息，确定相应的坐标变换算法；

（2）读取离线编制的理想数控加工程序段N；

（3）数据分离，获取理想数控加工程序段N中刀位点坐标值、转角及摆角信息；

（4）计算补偿量ΔX、ΔY、ΔZ；

（5）理想数控加工程序段N重新赋值＝＋ΔX，＝＋ΔY，＝＋ΔZ；

（6）返回步骤2。

基于UG NX利用TCL语言开发的WFL M120 MILLTURN车铣复合加工中心五轴联动数控加工时旋转中心偏移补偿量的自动计算的后置处理算法[6]为：

proc PB_CMD_Manaul_calculate_comprehension { } {

global mom_pos

global mom_out_angle_pos

MOM_output_literal "R41=[format "%.3f" $mom_out_angle_pos(0)]"

MOM_output_literal "R42=[format "%.3f" $mom_out_angle_pos(1)]"

MOM_output_literal "@630 R45 R41"

MOM_output_literal "@631 R46 R41"

MOM_output_literal "R36=R5*R46"

MOM_output_literal "R31=[format "%.3f" $mom_pos(0)]+R36"

MOM_output_literal "R32=[format "%.3f" $mom_pos(1)]"

MOM_output_literal "R37=R5*R45"

MOM_output_literal "R33=[format "%.3f" $mom_pos(2)]-R37"

}

WFL M120 MILLTURN机床加工某零件的带有旋转中心偏移自动补偿的数控加工程序为：

N0001 %MPF362

N0002 ;Programmer: ScjxZkui Fri Jul 13 18:27:32 2018

N0003 R1=400.000 ;Tool length

N0005 R21=0 ;comprehension

N0006 R5=229.981+R1+R21 ;Pivot distance

N0007 G0 G90 G40 G71 G54 D0;

N0008 T1=3 R1=1 R3=0 R4=0 L106 ;Tool change

N0009 L918 ;milling model

N0010 M3=61 ;S3 milling-spindle

N0011 M3=150 ;relax c-axis

N0012 M6=150 ;Relax B1-axis

N0013 G0 G90 G54 G64 D0 Y1=0

N0014 M3=8 ;inner coolant on

N0015 M1=126

N0016 S3=1200 M3=03

N0025 R41=-0.147

N0026 R42=188.282

N0027 @630 R45 R41

N0028 @631 R46 R41

N0029 R36=R5*R46

N0030 R31=300.467+R36

N0031 R32=-77.731

N0032 R37=R5*R45

N0033 R33=-142.085-R37

N0034 G00 G90 Y1=R32 Z1=R33 B1=-.147 C1=188.282

N0035 G00 E1=R31

……

3 结束语

一些中高档数控系统已成功开发旋转中心偏移自动补偿功能，如Heidenhain_iTNC530系统中的M114，编程人员只须在CAD/CAM软件中按工件坐标系编制刀位点运动轨迹和每一刀位点的刀轴矢量，然后根据机床结构特点及旋转中心偏移量为零的理想状态后置处理，操作人员在数控系统规定的参数下输入实际的旋转中心偏移量，系统执行程序过程中会自动计算补偿后的刀位点轨迹从而进行实时控制。

本文中提出的算法和基于该算法开发的自动补偿编程软件，特别适用于还不具备旋转中心偏移自动补偿功能的数控系统，MCS位置、机床与刀具几何参数存放于程序内相应变量中，刀位点的移动位置在程序中进行自动计算，调整相应的参数让程序的重复使用变得可能。

[1]刘伟雄，等. 数控加工理论与编程技术[M]. 北京：机械工业出版社，2000.

[2]蔡永林，席光，查建中. 五坐标数控加工后置处理算法研究[J].组合机床与自动化加工技术，2003（9）：17-20.

[3]王华侨. 实用数控加工技术应用与开发[M]. 北京：机械工业出版社，2007.

[4]林勇，彭芳瑜. 五轴联动的后置处理系统设计与实现[J]. 机电工程技术，2005（9）：73-74.

[5]Donald Hearn，M. Pauline Baker. Computer Graphics (Second Edition)[M]. USA：Prentice Hall/Pearson，1994.

[6]张磊. UGNX6后处理技术培训教程[M]. 北京：清华大学出版社，2009.

The Algorithm of Compensation for Rotary Center Offset in 5-Axis NC Machining

ZHUANG Ying1，ZHOU Kui2

( 1.Sichuan Provincial Machinery Research & Design Institute, Chengdu 610063, China; 2.Sichuan Engineering Technical College, Deyang 618000, China )

In 5-axis NC machining, MCS ( Machining Coordinate System ) is the basis for the movement of machine tools and it is the basis for NC program, the location of the control pointP＝P'＋ΔP, P'is the base, it is calculated by the center of the rotation axis coincides with the origin of the MCS. The other component ΔPis due to the center of the rotation axis does not coincides with the origin of the MCS, which causes the difference in the position of the assumed position and the position of the tool loci in the program. In this paper, the calculation formula of the position compensation for the position of the control point is studied. The post processing program is developed which can automatically generate the NC program with the automatic compensation function of the rotation center offset. It is suitable for the 5-axis machining program which does not have the function of RTCP and the rotation center offset automatically.

5-axis；NC machining；coordinates transformation；rotary center；offset；compensation；algorithm

TP391.72

A

10.3969/j.issn.1006-0316.2018.07.018

1006－0316 (2018) 07－0077－04

2018－03－09

庄瑛（1969－），女，四川成都人，本科，主要研究方向为机械制造与自动化；周奎（1973－），男，四川渠县人，工程硕士，教授，主要研究方向为数字化制造及自动检测。