关于路和圈的3-色Ramsey数
2018-08-07李雨生
陈 明, 李雨生
(1. 同济大学 数学科学学院, 上海 200092; 2. 嘉兴学院 数理与信息工程学院, 浙江 嘉兴 314000)
1 研究背景
本文研究的图均为简单无向图.设G是一个图,其点集和边集分别为V(G)和E(G),并分别用n(G)、Δ(G)和δ(G)表示图G的阶数、最大度以及最小度.Pn和Cn分别表示由n个点构成的路和圈.图G中最大的圈长称为该图的周长,用c(G)来表示.其他有关图的定义,可参考文献[1].
对于给定的图G1,G2,…,Gk,k≥2,k-色Ramsey数R(G1,G2,…,Gk)是指最小的正整数n,使得对n个点的完全图进行任意的k-边染色,总是存在某个染i色的单色图Gi,1≤i≤k.若G1=G2=…=Gk=G,k-色Ramsey数R(G1,G2,…,Gk)简记为Rk(G),又称之为G的对角k-色Ramsey数.当k=2时,2-色Ramsey数通常简称为Ramsey数.
关于Ramsey数的研究成果非常丰富,详细可见动态综述文献[2].但对于k-色Ramsey数(k≥3)的研究结果相对较少,并且主要集中在对路和圈等结构比较明确的图的研究上.对于充分大的路和圈,其对角3-色Ramsey数已经明确:
定理1[3]设n充分大,则R3(Pn)= 2n-2+(nmod 2);
定理2[4]设n是一个充分大的偶数,则有R3(Cn)= 2n;
定理3[5]设n是一个充分大的奇数,则有R3(Cn)= 4n-3.
对于任意的n,很多学者猜测定理1~3也是成立的,但目前仅有少数情况得到验证.
对于路和圈的混合3-色Ramsey数,已有学者给出了一些准确值:
定理4[6]设n≥6,则R(P3,P3,Cn)=n;
定理5[7]设n≥6,则R(P4,P4,Cn)=n+2;
定理6[8]设n≥23,则R(P4,P5,Cn)=n+2,R(P4,P6,Cn)=n+3;
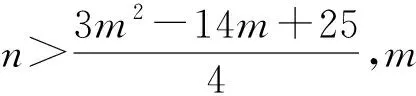
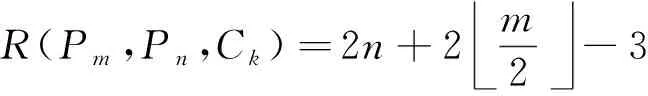
R(Pm,Pn,Ck)=2n+2m2-3
在此基础上,本文证明了:
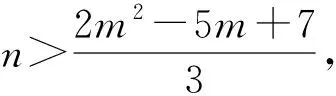
定理9设m为奇数,n>2m2-7m+8, 则R(Pm,Pm,Cn)=m+n-3.
2 主要结果的证明
为了证明定理8和定理9,将用到以下术语符号和定理.
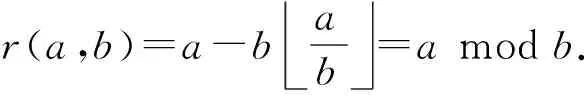
r(a,b)=a-bab=a mod b.
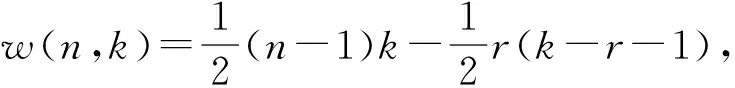

定理11[11]设G是一个有n个点和m条边的图,m≥n,且周长c(G)=k.则m≤w(n,k).
2.1 定理8的证明
当m≤4时,由定理5可知结论成立.以下设m≥6 .
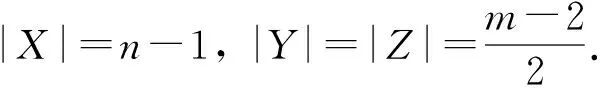
再证R(Pm,Pm,Cn)≤m+n-2,令N=m+n-2,只需证明任意3-边染色(三种颜色设为红、蓝和绿)的KN,至少含有红色的Pm、蓝色的Pm和绿色的Cn中之一.方便起见,分别称红(蓝、绿)边导出的子图为红(蓝、绿)子图.下面假设某3-边染色的KN,不含有红色的Pm,不含蓝色的Pm,也不含绿色的Cn,从而导出矛盾.
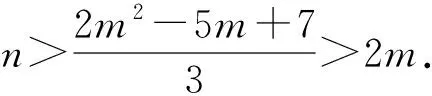

因为绿子图中不含有Cn,由定理10可知,绿子图的周长最大为n-1.再根据定理11,可知KN中绿边的条数至多为
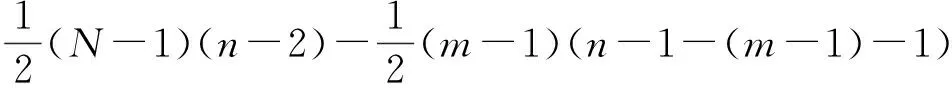
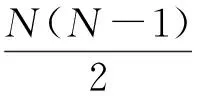
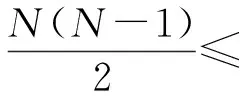
2.2 定理9的证明
当m=3时,由定理4可知结论成立.以下设m≥5 .
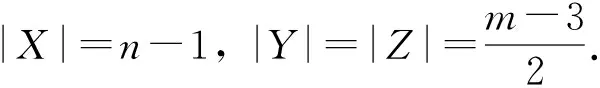
再证R(Pm,Pm,Cn)≤m+n-3,令N=m+n-3,只需证明任意3-边染色(三种颜色设为红、蓝和绿)的KN,至少含有红色的Pm、蓝色的Pm和绿色的Cn中之一.方便起见,分别称红(蓝、绿)边导出的子图为红(蓝、绿)子图.下面假设某3-边染色的KN,不含有红色的Pm,不含蓝色的Pm,也不含绿色的Cn,从而导出矛盾.
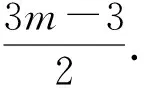

因为绿子图中不含有Cn,由定理10可知,绿子图的周长最大为n-1.再根据定理11,可知KN中绿边的条数至多为
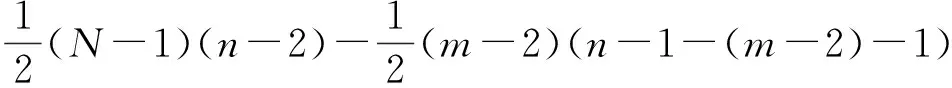
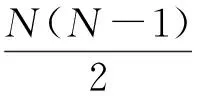
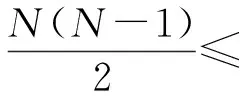
这和题设中的n>2m2-7m+8矛盾,定理9证毕.
鉴于目前所有的研究,给出一个大胆的猜测:
猜想对任意正整数n和m,且n≥m, 有R(Pm,Pm,Cn)=m+n-2-(mmod 2).
