基于加速寿命试验的自润滑关节轴承可靠性分析
2018-08-07邱明周大威周占生
邱明, 周大威, 周占生
(1.河南科技大学 机电工程学院, 河南 洛阳 471003;2.河南科技大学 机械装备先进制造河南省协同创新中心, 河南 洛阳 471003)
0 引言
自润滑关节轴承主要由外圈、内圈和自润滑衬垫3部分组成,衬垫粘结在外圈内球面上,其摩擦方式为衬垫层滑动表面对内圈外球面的滑动摩擦。随着航空、铁路和军工领域对高质量自润滑关节轴承需求量的逐渐增加[1-2],对自润滑关节轴承的使用寿命和可靠性要求也越来越高。
关节轴承可靠性试验是获取关节轴承失效信息、消除早期失效以及进行分析改进[3-4]、验证[5-6]并使关节轴承可靠性逐步得到增长,最终达到预定可靠性水平的重要基础。目前对自润滑关节轴承的研究主要针对其成膜机理和摩擦学性能[7-9],而对其可靠性研究还很少见。由于寿命是自润滑关节轴承最主要的一个可靠性特征量,一些学者和企业对其寿命进行了研究,例如,瑞典SKF公司[9]、日本NTN公司[10]、德国Schaeffler KG公司[11]、德国FLURO公司[12]等都提出了各自轴承的寿命计算公式。在国内,杨咸启等建立了适合国产关节轴承的寿命计算公式,并发布了关节轴承寿命计算的机械行业标准JB/T8565—2010[13]. 文献[14]基于组合磨损理论和稳定磨损中线磨损率保持不变的特征,推导出了新的解析式寿命模型,并提出了其磨损寿命的计算方法。文献[15]采用组合磨损计算方法建立了自润滑关节轴承的磨损寿命模型。上述文献都是针对自润滑关节轴承的寿命计算公式,难以直接反映自润滑关节轴承的可靠性。由于寿命试验是可靠性试验的一种形式,常规寿命试验时间较长、费用很高。为了缩短试验时间、降低试验成本,必须采用加速寿命试验[16-17],即在不改变自润滑关节轴承失效机理的条件下,用加大应力的方法对关节轴承进行寿命试验。
本文利用自主研发的向心关节轴承加速寿命试验机[18]对关节轴承进行恒定应力下的加速寿命试验,为实现对自润滑关节轴承的可靠性分析提供了试验依据;基于试验数据进行Weibull分布假设检验及参数估计,得到了自润滑关节轴承在不同加速应力下的可靠性指标,并外推出自润滑关节轴承在正常应力下的可靠度函数,实现了自润滑关节轴承的可靠性分析。
1 自润滑关节轴承加速寿命试验方法
1.1 试验设备和试验轴承样品
采用自主设计制造的关节轴承加速寿命试验机对关节轴承进行试验,该试验机可以同时安装4套自润滑关节轴承,采取液压加载方式,并通过温度传感器和位移传感器对每套关节轴承的摩擦温升和磨损量进行在线实时监测。试样为同一批生产的自润滑关节轴承(见图1),其基本尺寸为内圈内径d=20 mm,球径ds=29 mm,内圈宽度B=16 mm,外圈外径D=35 mm,外圈宽度C=12 mm,内圈外球面进行镀铬处理。
1.2 加速寿命试验条件
试验条件如下:1)在相同的室温下进行试验。2)旋转摆动角度为±6°. 3)摆动频率f=2.38 Hz. 4)选取载荷作为关节轴承加速寿命试验的加速应力,并设置加速应力水平数k=3,分别为10 kN、13 kN、17 kN (300≤pv≤3 000[19],单位:MPa·mm/s,pv为名义接触压力p和球面滑动速度v的乘积)。5)采用定数截尾试验方法,对于恒定应力加速寿命试验,各加速应力水平下关节轴承的失效数一般应不少于4个[20]。为充分利用试验机的效率,每4套轴承为一组进行试验,在相同加速应力下共做3组试验,即每组加速应力试验关节轴承总数n=12套。每组至少有1套关节轴承失效时停机,并分析关节轴承的失效时间和失效数量,同一组失效的轴承失效时间取相同值。6)试验终止条件为轴承的摩擦温升达到35 ℃以上或轴承出现异常噪音。轴承的失效时间是根据摩擦温度出现突变升高选取的,如果在摩擦温升到达25 ℃时关节轴承温升快速上升,则取温升25 ℃前的试验时间为轴承寿命。
2 自润滑关节轴承寿命试验数据分析
2.1 基本假设
为了得到关节轴承的可靠性指标,需要对寿命数据进行统计分析。本文采用较成熟的经典统计分析方法处理其寿命数据。
对于自润滑向心关节轴承,其主要的失效方式为衬垫的磨损失效。假设在载荷应力下其寿命分布服从两参数Weibull分布,从而可得在第i组试验应力下的概率分布函数为
(1)
式中:t为轴承的试验时间,t>0;i为加速应力水平的顺序号;mi和ηi分别为第i组加速应力水平的形状参数和特征寿命。
假设1分布同族性假设。关节轴承在不同加速应力下得到的寿命数据均服从Weibull分布。
假设2失效机理一致性假设。关节轴承在不同加速应力下的失效机理没有改变。Weibull分布的形状参数m决定了关节轴承的失效机理,因此不同加速应力下所得的形状参数基本相同,即在Weibull分布概率图上基本是一簇平行直线。
假设3关节轴承加速寿命方程为
lnη(S)=a+bφ(S),
(2)
式中:η(S)为特征寿命,S为应力;a和b为加速寿命方程系数;φ(S)为应力S的已知函数。
2.2 Weibull分布的拟合检验方法
在对关节轴承进行加速寿命试验后,可得到一系列寿命试验数据。通过对这些寿命数据进行统计分析,可以得到关节轴承的各种可靠性特征量。但是,在分析之前,并不清楚这些寿命数据是否服从Weibull分布,因此需要对所得到的数据进行拟合检验。本文所采用的方法是概率图检验法和F检验法两种方法。
2.2.1 概率图检验法
首先,从中位秩表[21]得到其概率分布函数的估计值;然后,将各加速应力水平下的数据点(lnt,ln[ln(1/(1-Fi(t)))])画到Weibull概率图上。
2.2.2F检验法
假设H0:Fi(t)=1-exp [-(t/ηi)mi]. 本试验的试验样本是随机抽样得到的,因此可以由抽样分布定理,利用F分布和极值分布的特点给出检验统计量如下:
(3)
(4)
式中:r*为定义的参数;r为失效个数;j为失效轴承的顺序号;lj为定义的标准间隔;tj为第j个失效轴承的试验时间;Zj为服从极值分布的变量;E(Zj)可由可靠性试验用表[21]查得。

W~F(2(r-r*-1),2r*),
(5)
则在给定显著性水平α下,接受假设H0的情况为
F1-α/2(2(r-r*-1),2r*)≤W≤
Fα/2(2(r-r*-1),2r*),
(6)
式中:上侧分位数Fα(f2,f1)可由F分布的分位数表查得。
2.3 Weibull分布可靠性特征量估计
对各加速应力水平的分布参数估计有多种方法。考虑到本文的试验样本数量较小(n≤25)且是恒定应力下的定数截尾加速寿命试验,因此采用最佳线性无偏估计(BLUE)法进行分布参数估计。其具体过程如下:
1)将每组加速应力下关节轴承的试验时间从小到大排列,则各应力水平下极值分布中的参数σi和μi的估计值可由(7)式计算:
(7)
式中:ni和ri分别为关节轴承在第i组加速应力下的试验样本总数和失效个数;tij为第i组加速应力下第j个失效轴承的试验时间;C(ni,ri,j)、D(ni,ri,j)分别为极值分布中参数σi和μi的最佳线性无偏估计系数;gri,ni为纠偏系数,可由可靠性试验用表查出。
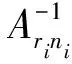
(8)
3)在应力水平Pi下的特征寿命估计为
ηi=exp (a+blgPi).
(9)
4)可靠度估计。由(1)式可推导出关节轴承的可靠度、可靠寿命和失效率等可靠性指标的数学表达式分别如下:
可靠度函数R(t)为
(10)
可靠度为R的可靠寿命tR为
(11)
关节轴承的平均寿命te为
(12)
失效率函数λ(t)为
(13)
3 实例分析
采用载荷作为加速应力,试样的摆动方式为旋转摆动,且试验摆动频率为2.38 Hz. 在此条件下设置3个加速应力水平,应力值Pi分别取为10 kN、13 kN、17 kN. 取自润滑关节轴承的正常载荷为P0=5 kN(pv≤300)。表1所示为寿命试验参数及所得的寿命数据。用表1中的数据进行分析处理,具体评估过程如下。

表1 加速寿命试验数据
3.1 分布检验
3.1.1 概率图检验法
由图2可知,在不同加速应力水平下的试验数据点基本分布在一条直线上,因此可以认为关节轴承的寿命服从Weibull分布;而且试验的寿命数据在Weibull分布概率图上基本是一簇平行直线,说明关节轴承在加速过程中其失效机理未发生改变。
3.1.2F检验法
第3组加速应力P3=17 kN时,试验样本为12,失效数为5. 由可靠性试验用表可以得到拟合检验结果如表2所示。
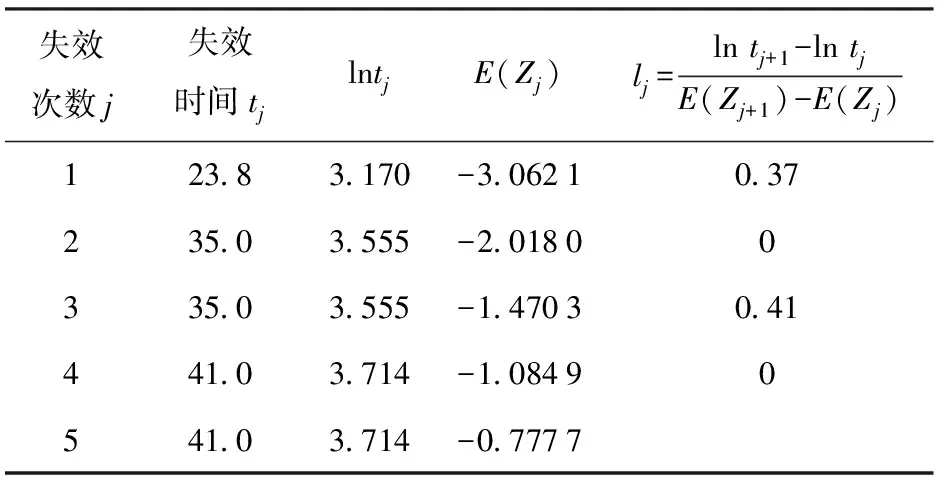
表2 Weibull分布的拟合检验
由表2可知r=5,因此r*=2. 根据(3)式计算出第3组加速应力下的检验统计量W3=1.11. 给定显著水平α=0.1,得F0.05(4,4)=6.390,F0.95(4,4)=0.157. 因此F0.05(4,4)>W3>F0.95(4,4). 故认为该加速应力下的关节轴承寿命服从Weibull分布。
同理,根据上述计算方法对另外两组加速应力下的寿命数据进行处理分析。得到第1组和第2组加速应力下检验统计量分别为W1=0.31,W2=1.20,F0.05(4,4)>W1>F0.95(4,4),F0.05(4,4)>W2>F0.95(4,4)。因此可以认为自润滑关节轴承的寿命服从Weibull分布。
3.2 各应力下关节轴承的可靠性评估
利用最佳线性无偏估计法对得到的寿命数据进行参数估计,得到关节轴承在各个应力下的分布参数估计值,然后将参数估计值分别代入(9)式~(13)式中,求出可靠性指标如表3所示。
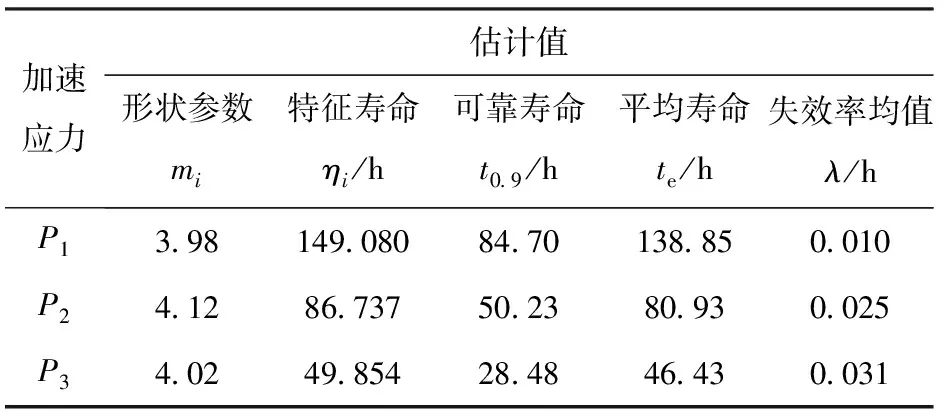
表3 各可靠性指标分析结果
利用表3得到的参数估计值,可以绘制出各加速应力水平下关节轴承的可靠度曲线,如图3所示。
3.3 正常使用条件下关节轴承的可靠度评估
从表3的参数估计值可以看出:经过检验(图2中也可以看出)可以认为形状参数m的估计值是一致的,表明关节轴承在加速过程中的失效机理未发生改变,因此可以利用加速模型外推出关节轴承在正常使用条件下的分布参数η0. 加速模型为(2)式,因此可以利用表3的数据计算得到加速模型的参数估计值:a=9.757 7,b=-4.753 3,从而得到正常使用条件下关节轴承失效寿命的分布参数[22]为
(14)
η0=exp(a+b×lgP0)=
exp(9.757 7-4.753 3×lg 5)=623.51,
(15)
式中:m0和η0分别为正常应力下的形状参数和特征寿命;n1、n2和n3为各应力水平试验的截尾数;m1、m2和m3为各应力水平的形状参数最佳线性无偏估计值,如表1和表3所示。
于是,关节轴承在正常使用载荷下,在给定时间t的可靠度为
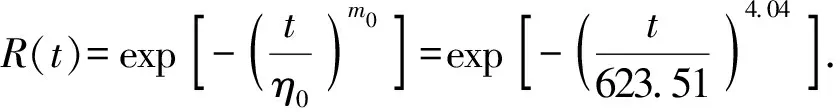
(16)
当R(t)=90%时,由(16)式可解得自润滑关节轴承的可靠寿命为t0.9=357.23 h;由(12)式可得自润滑关节轴承的平均寿命为te=565.47 h.
3.4 试验验证
为了验证上述正常应力下可靠性指标预测值的可靠性,必须对预测结果进行试验验证。在加速应力P0=5 kN、试验摆动频率f0=2.38 Hz条件下,对同一批生产的自润滑关节轴承仍采用定数截尾的试验方法,所得正常应力下的寿命数据为368.7 h、 476.8 h、 476.8 h、 582.3 h、 582.3 h. 结合上述3种加速应力下的寿命数据,采用BLUE法对正常应力下的寿命数据进行参数估计,所得结果如表4所示。
从表4中可见,正常应力条件下的验证值与预测值基本一致,特征寿命、可靠寿命、平均寿命误差均在10%以下,而形状参数误差只有0.7%,说明加速寿命试验是可行的,此预测方法能较好地预测自润滑关节轴承在正常应力下的可靠性。

表4 正常应力下各可靠性指标的试验验证
4 结论
本文基于加速寿命试验的寿命数据及可靠性分析方法,针对自润滑关节轴承的寿命可靠性进行了研究。得出以下结论:
1)各加速应力下的自润滑关节轴承寿命服从Weibull分布。
2)自润滑关节轴承在加速过程中其失效机理并未发生改变,验证了加速寿命试验的可行性。
3)正常应力下自润滑关节轴承的寿命可靠性验证值与预测值基本一致,验证了本文所提预测方法的正确性。
