头部非对称刻槽弹体侵彻混凝土目标性能研究
2018-08-07邓佳杰张先锋刘闯庞春旭王文杰
邓佳杰, 张先锋, 刘闯, 庞春旭, 王文杰
(1.南京理工大学 机械工程学院, 江苏 南京 210094; 2.西安现代控制技术研究所, 陕西 西安 710065)
0 引言
动能侵彻弹是打击深层目标的有效手段,其借助于高动能驱动侵入靶体内部实现对混凝土类目标的有效破坏。当前,动能侵彻弹的研究主要通过提高冲击速度及增加弹体初始质量的方式来提高侵彻动能,通过高动能对混凝土进行震碎和挤压破坏,而采用单一压缩破坏混凝土模式的动能侵彻弹对其侵彻能力局限较大。因此,摆脱传统侵彻模式的新原理、新结构动能侵彻弹设计开发及其侵彻机理研究已逐渐成为新型钻地武器研究热点之一。
研究者们开展了大量关于侵彻弹头部形状对侵彻深度影响及头部形状优化的研究工作。Yankelevsky等[1]基于土盘模型,分析了弹体头部形状对砂土侵彻深度的影响,提出了最小化阻力的弹体头部形状优化方法,仅利用侵彻阻力、侵彻速度及靶体模型得到回转体弹形最优化结构。文献[2-3]基于弹体头部形状系数表示方法,分析最小阻力下最优化头部形状系数,进而提出了双卵形头部弹体优化设计方法,并通过仿真及试验验证了该弹形优异的侵彻能力。Ben-Dor等[4-5]基于局部相互作用模型提出关于头部形状相关的侵彻深度模型,并基于最优化控制理论确定多种回转体头部形状的最优化外形轮廓。Mayersak[6]、柴传国[7]在卵形弹体头部尖端增加圆柱段,开展了该异型结构弹体侵彻混凝土试验,并提出了相应的侵彻深度计算模型。对于回转体弹形而言,优化方法受其结构限制,优化后弹形侵彻深度提高有限。Ragnedda等[8]提出了切平面卵形头部弹体侵彻混凝土深度模型。Yakunina[9-11]基于局部相互作用模型提出了凸星形头部及V形槽锥形头部弹体侵彻半无限靶深度计算模型,并给出了弹形优化设计方法。范少博等[12]分析了直槽及螺旋槽头部结构弹体侵彻阻力,并通过试验及仿真确定了螺旋槽弹体在提高侵彻深度方面的优势。Erengil等[13]提出了具有卵形头部和锥形弹身刻槽的高速侵彻新概念弹(CPHP),随后梁斌等[14]、Wu等[15]、He等[16]通过高速侵彻深度试验及考虑头部侵蚀效应的侵彻理论模型分析确定了CPHP的侵彻能力,但高速侵彻侵蚀情况时CPHP侵彻能力受限于弹体材料。Zhang等[17]开展了双卵形弹体及CPHP侵彻对比试验,并提出了相应的理论分析模型,分析结果表明双卵形弹体能够有效提高弹体侵彻能力,同时CPHP具有较好的侵彻弹道稳定性。庞春旭等[18-19]设计了弹体头部刻蚀对称槽及非对称槽结构,在旋转侵彻半无限厚混凝土、铝靶试验及仿真研究基础上,分析得出头部非对称刻槽配合旋转效应可有效提高弹体侵彻深度。
本文基于弹体压剪破坏混凝土思想,提出一种头部非对称刻槽弹体并在柱坐标下表征其几何结构。结合准静态柱形空腔膨胀模型,引入剪切作用下的靶体受力状态,建立轴向压缩- 切向剪切联合作用下的准静态柱形空腔膨胀理论模型,推导得到考虑剪切效应的靶体响应力函数。在此基础上,提出头部非对称刻槽弹体侵彻半无限厚混凝土目标侵彻深度局部相互作用模型。同时,开展头部非对称刻槽弹体与尖卵形弹体侵彻混凝土目标对比试验研究,通过理论及试验侵彻深度结果确定非圆截面头部弹体的锐化作用在提高侵彻性能上的优势。结合头部非对称刻槽弹体侵彻过程计算结果,分析头部非对称刻槽弹体的侵彻阻力和侵彻深度变化规律。
1 头部非对称刻槽弹体结构表征与侵彻动力学模型
1.1 头部非对称刻槽弹体结构表征
基于混凝土材料压缩与剪切特性,通过改变弹体头部结构形式实现对混凝土材料的有效剪切作用,是加速破坏混凝土并提高弹体侵彻深度较为有效的途径。在能量利用率上,侵彻过程弹体动能损耗作用在剪切混凝土上的破坏效能显著高于压缩混凝土。本文基于混凝土材料抗压不抗剪的特点,提出一种通过头部刻槽实现非对称结构形式的弹体。该类型弹体在侵彻过程中可改变传统结构弹体侵彻单一压缩破坏混凝土的模式,最大化地破坏混凝土材料,从而减小侵彻过程阻力,实现较优的弹体侵彻毁伤能力。
弹体头部刻槽的非对称结构形式是指单个槽中无对称面,且非对称槽头部弹体侵彻过程中槽面受力在垂直于弹体轴线平面内无法抵消,绕弹体轴线产生一定的偏转力矩。以图1中具有4个槽的头部非对称刻槽弹体为例,由图1(b)可以看出槽仅在弹体中轴线一侧,单一槽在头部剖面上呈现非对称形状,由此定义该类型弹体为头部非对称刻槽弹体。
头部非对称刻槽弹体几何尺寸定义由两部分组成:基体尖卵形弹体几何尺寸和非对称槽头部结构几何尺寸。图2(a)为头部非对称刻槽弹体的OXY剖面视图,弹体头部长度为b,弹体半径为rp,弹体头部圆弧半径为Sr,槽长度为Lu. 非对称槽起始点为x0,铣槽角度为α,铣槽数为n.

Lg=fo(x0)+(x-x0)tanα.
(1)
非对称槽主受力面HR段的长度hm为
hm=fo(x)sinγ,
(2)
式中:
(3)
非对称槽主受力面RM段的长度hs为
hs=fo(x)-fo(x0)-(x-x0)tanα.
(4)
由于非对称槽区域的不连续性,非对称槽的轮廓在HR段表达式是关于θ的函数。非对称槽轮廓表达式可统一表示为

(5)
式中:k=0, 1, 2, …,n-1.
根据非对称性槽起始点及非结称槽长度的不同,柱坐标(x,ρ,θ)下非对称槽头部弹体轮廓f(x,θ)采用分段表示方法,由基体弧区域和非对称槽区域组成。
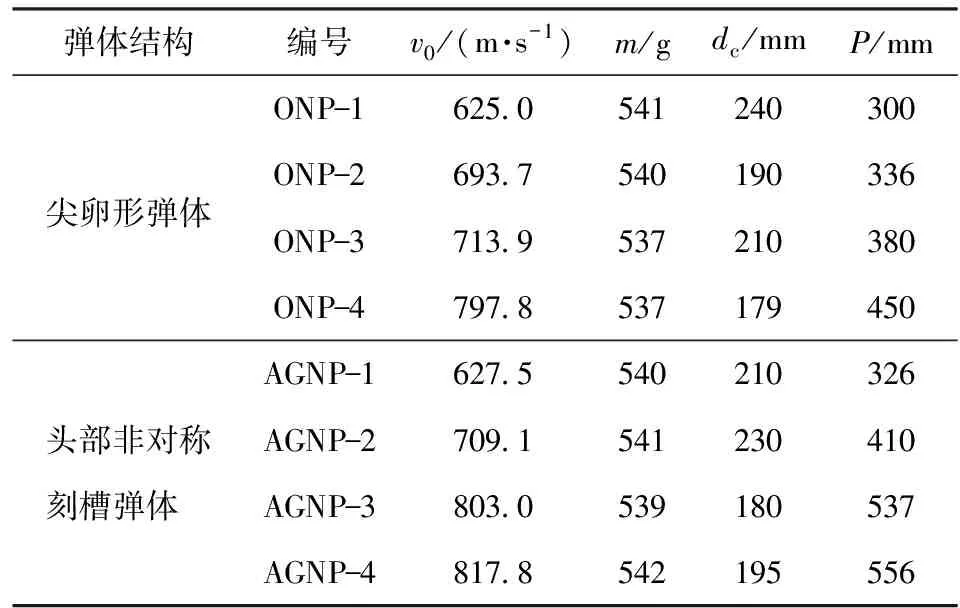
在0≤x f(x,θ)=fo(x). (6) 在x0≤x (7) 在b≤x (8) 基于一维坐标下的准静态柱形空腔膨胀理论,引入剪切效应,推导考虑剪切效应的二维准静态柱形空腔膨胀模型,得到相应的靶体响应力表达式,继而可深入分析和研究轴向压缩- 切向剪切联合作用下混凝土材料破坏特性及弹体的侵彻行为。 假设在头部非对称刻槽弹体侵彻作用下,混凝土材料中出现柱形空腔。此时,柱形空腔壁面以速度vc及旋转角速度ω由初始零半径向外径向膨胀,混凝土材料在受径向应力的同时在各响应区间产生周向旋转作用,材料受力表现为轴向压缩及切向剪切联合作用力,此时柱坐标下的空腔膨胀过程为二维受力状态。如图3所示,材料在准静态柱形空腔膨胀理论下的响应可描述为:空腔区(0≤rc 根据图3所示的靶体响应区,弹性区是处于r=cct到r=cet的区域圆环面,在r=cet处到达未受扰动区边界,该位置处的所有应力均为0. 柱坐标系下,各向应变与位移间关系可表示为 (9) 弹性区各应力与应变间的关系可表示为 (10) (9)式和(10)式中:ur、uθ分别为介质的径向位移和切向位移;σr、σθ、σz分别为介质的径向应力、切向应力和轴向应力;σrθ、σrz、σθz分别为介质在rθ平面、rz平面及θz平面的剪切应力;εr为介质的径向应变;εθ为介质的切向应变;εθr为介质的剪切应变;G和λ为介质的剪切模量和Lame系数,其表达式分别表示为 (11) E为材料弹性模量,μ为材料的泊松比。 将微元体所受力投影到微元体rθ平面上,根据二维状态下的微元受力分析,可得到微元径向及rθ平面的平衡方程为 (12) 由微元平衡方程关系,可得到各向应力与位移微分方程的表达式 (13) 弹性区域满足胡克定律,塑性区应力关系的求解中,假设材料的屈服遵循von Mises屈服面。 (14) 式中:τrθ为rθ平面的剪切应力;fc为混凝土材料无围压强度。 在平面应变状态的圆柱坐标下,z方向的应变、应变率和塑性应变率均为0,z方向的应力可由径向应力和切向应力给出,即 (15) 由以上推导得到屈服面上的应力关系式: (16) 根据二维平面(r,θ)条件下各向应力与位移间的关系式、微元径向及rθ平面的平衡方程和各向应力与位移微分方程,可以得到径向位移与切向位移间的微分方程形式: (17) 微分方程形式的(17)式为2阶常系数齐次线性方程组,其一般解可表示为 (18) 式中:C1、C2、D1、D2为2阶常系数齐次线性方程组解的常数项。 对于边界条件r趋近于无穷时,二维平面(r,θ)的径向位移及切向位移均为0,即C1=D1=0. 结合边界条件,将(18)式代入(13)式,可得到各向应力与位移微分方程: (19) 假设切向位移uθ与径向位移ur满足线性比例关系,即 (20) 旋转角速度ω与径向速度vc同时满足(20)式的线性比例关系,即 (21) 在考虑切向位移的条件下,屈服面半径为Ccs. 将(19)式代入(16)式的屈服条件,得到常数项C2和D2的表达式: (22) 当考虑材料为不可压缩性材料时,柱形空腔膨胀模型的质量守恒关系可表示为 (23) 式中:acs为空腔膨胀到达屈服条件时的空腔半径。 将(22)式代入(18)式,得到空腔膨胀到达屈服条件下径向位移关系式: (24) 由(24)式可进一步得到空腔膨胀到达屈服条件时的空腔半径acs与初始空腔半径a0及屈服面半径Ccs的关系,即 (25) 式中:M1可表示为 (26) 根据平衡方程,结合(19)式、(22)式和(25)式,可得到考虑剪切效应的靶体空腔膨胀径向应力随空腔膨胀过程中空腔半径间的关系式: (27) 空腔达到稳定时,空腔壁面径向应力趋近于稳定,此时该径向应力即为空腔膨胀径向应力值。 根据(27)式分别计算空腔稳定时的无剪切效应及存在剪切效应的空腔膨胀径向应力表达式,给出剪切效应弱化靶体响应力的无量纲因子为 (28) 借助于Forrestal等[20]提出的半经验响应力函数式,结合剪切效应弱化靶体响应力的无量纲因子,可得到头部非对称刻槽弹体侵彻下靶体的响应力函数: (29) 式中:ρt为混凝土材料的密度;a0和a2为混凝土材料的相关常数。 由此,头部非对称刻槽弹体表面各受力面的靶体响应力函数由(29)式计算获得。 头部非对称刻槽弹体表面法向应力可分为3部分:基体弧面、非对称槽主受力面和非对称槽从受力面。头部非对称刻槽弹体表面法向响应力的表达式为 (30) 式中:β为基体弧区域微元切向与速度方向的夹角;σnHR、σnRM和σno分别表示非对称槽主受力面、非对称槽从受力面和基体弧面微元表面法向响应力;vω为非对称槽从受力面上微元的绕弹轴瞬时旋转角速度ω对应的线速度,非对称槽区域的任意微元对应的线速度可表示为 vω=fL(x,θ)ω. (31) 弹体非对称槽主受力面法向响应力与弹轴呈90°-α角度,非对称槽主受力面微元表面法向响应力如图4所示,可分解为阻碍弹体轴向运动和影响弹体周向旋转运动的两个,其值分别为σxHR和σωHR. 弹体非对称槽从受力面法向响应力垂直于受力面,非对称槽从受力面微元表面法向响应力不参与阻碍弹体轴线运动,仅影响弹体周向旋转运动。 根据头部非对称刻槽弹体几何关系及表面法向响应力表达式可确定,长度为dx的头部非对称刻槽弹体表面在弹体轴线方向上的轴向侵彻阻力表达式为 (32) 头部非对称刻槽弹体侵彻过程为垂直侵彻,侵彻过程分为开坑侵彻和隧道侵彻两个阶段。由此,头部非对称刻槽弹体侵彻半无限脆性靶的侵彻深度可表示为 (33) 式中:Pc为开坑区侵彻深度,其值由Pc=2rp·[0.707+b/(2rp)][21-22]计算得到。 任意x坐标位置处长度为dx的弹体非对称槽主受力面绕弹体轴线旋转的力矩为 (34) 任意x坐标位置处长度为dx的非对称槽从受力面绕弹体轴线旋转的力矩为 (35) 任意x坐标位置处长度为dx的头部非对称刻槽弹体绕弹轴旋转的合力矩为 (36) 头部非对称刻槽弹体的周向合力矩表达式为 (37) 式中:p为弹体瞬时侵彻深度。 由动量矩定理,得到头部非对称刻槽弹体绕弹轴旋转的微分方程: J(dω/dt)=mω(dω/dη)=-M= (38) 式中:J为弹体绕x轴的转动惯量;η为头部非对称刻槽弹体瞬时旋转角度。 在头部非对称刻槽弹体侵彻计算过程中,利用差分计算方法,由(37)式和(38)式得到瞬时旋转角速度ω,将该时刻的旋转角速度与侵彻速度比值代入(29)式即可得到相应时刻的靶体响应力数值,进而利用微元(32)式在弹体受力区域进行积分得到弹体阻力。根据上述计算步骤,对弹体侵彻过程进行离散化计算,直至到达边界条件弹体侵彻速度v≤0或弹体旋转角速度ω≤0停止计算,侵彻深度及侵彻阻力时程曲线由此得到。 下面采取对比试验方法,分别设计同口径的传统尖卵形弹体及头部非对称刻槽弹体,通过侵彻深度及侵彻后靶体破坏形式的比较分析,来分析头部非对称刻槽弹体的侵彻行为。参考头部非对称刻槽弹体结构表征方法,设计尖卵形弹体和头部非对称刻槽弹体。弹体直径2rp=30 mm,弹体长径比Lp/(2rp)=6,卵形头部曲径比 (CRH)均为4. 非对称槽起始点x0、铣槽角度α和铣槽数n分别为2 mm、13.6°和4. 弹体材料硬度为45.5 HRC,假设弹体为刚性,图5为弹体实物图。本试验开展30 mm弹体侵彻混凝土目标的侵彻深度对比试验研究。弹体采用φ30 mm滑膛炮加载,侵彻速度由测速锡箔靶及多通道测速仪组成的测速系统来确定。混凝土目标设计尺寸为φ1 000 mm×1 000 mm,靶体外部包裹8 mm厚钢板以防止混凝土碎裂解体。设计混凝土质量配比为水泥∶骨料∶水=1.00∶1.25∶0.35,骨料选用石英石中粗砂细骨料,骨料粒径足够小,以避免侵彻过程中对头部刻槽弹体侵彻弹道造成影响。标准28 d养护周期完成后对靶体材料力学性能进行测试,得到靶体无围压强度fc为45 MPa,弹性模量E为33.5 GPa,泊松比μ为0.22. 由图5可见,弹体头部非对称槽可引起侵彻过程中弹体头部周向产生孤立面,并造成非对称槽主受力面和从受力面靶体响应力分布不均匀,导致弹体产生旋转扭矩进而使得弹体边侵彻边旋转。图6为试验后回收头部非对称刻槽弹体照片。如图6所示,侵彻后弹体未产生变形,侵彻过程可视为刚性侵彻。侵彻后弹体表面附着的混凝土主要集中于槽末端至弹体尾部的弹体圆柱部,弹体表面附着混凝土的起始和末端不在同一母线上,附着的混凝土轨迹在弹体弹身段表面具有一定的弧度且与槽从受力面所在轴线位置间有夹角。从弹体侵彻方向看,弹体绕弹轴线顺时针方向自旋。图7给出了头部非对称刻槽弹体侵彻混凝土后的靶体失效破坏情况。由图7(a)中靶面开坑照片可以看出,弹体侵彻后靶体均出现漏斗状弹坑。由图7(b)的侵彻弹道照片可以看出,弹体进入稳定侵彻段时,头部非对称刻槽弹体侵彻孔道存在有因刻槽区域压实混凝土造成的孔道壁面混凝土凸起,其长度贯彻整个稳定侵彻区孔道,凸起位置对应于弹体的刻槽区域。表1给出了尖卵形弹体与头部非对称刻槽弹体侵彻深度的试验值。表1中dc表示开坑直径,两种结构弹体开坑直径相近,平均开坑直径约为210 mm. 通过对试验数据进行多项式拟合,得到图8所示两种弹体结构的侵彻深度对比结果。从图8所示的试验数据及拟合曲线可以看出,弹体头部非对称刻槽结构能够显著提高弹体的侵彻深度。侵彻速度的增加有利于头部非对称刻槽弹体的侵彻,随着侵彻速度的增加,头部非对称刻槽弹体相对尖卵形弹体的侵彻深度提高率增加。 表1 尖卵形弹体与头部非对称刻槽弹体侵彻深度试验值 结合2.1节的头部非对称刻槽弹体侵彻试验数据,对本文提出的头部非对称刻槽弹体侵彻混凝土深度局部相互作用模型进行试验验证。以尖卵形弹体及头部非对称刻槽弹体侵彻试验作为校核算例,将试验初始条件及弹体尺寸参数作为模型计算输入。 图9为尖卵形弹体和头部非对称刻槽弹体侵彻45 MPa混凝土目标的侵彻深度试验与理论模型计算对比结果。由对比结果可以看出,理论模型预测的侵彻深度与试验值吻合较好,弹体侵彻深度理论值相对误差最高为5.36%. 由此,在头部非对称刻槽弹体的局部相互作用侵彻模型中引入剪切效应的靶体响应力函数,能够较准确地计算头部非对称刻槽弹体侵彻混凝土的侵彻深度。根据试验校核结果可以看出,该模型在预测不同尺寸、不同头部非对称刻槽长度及不同靶体强度条件下具有较好的适用性和准确性。 为了进一步分析头部非对称刻槽弹体的侵彻机理,对试验中两个速度段的头部非对称刻槽弹体及相应的尖卵形弹体侵彻过程参量进行对比。图10分别给出(630±10) m/s和(800±10) m/s两个速度段的侵彻加速度和侵彻深度时程曲线。由加速度时间曲线对比结果可以发现,侵彻速度相近的条件下,头部非对称刻槽弹体在侵彻开坑结束后加速度到达的峰值较低,进入隧道区稳定侵彻阶段时加速度相对较小且侵彻时长较短,该阶段阻力减小主要为弹体头部锐化作用引起的,靶体材料剪切弱化作用效果较小。在侵彻中后段由于弹体的自旋作用使混凝土材料受到剪切,造成其强度减弱,混凝土目标体阻抗进一步减小,弹体所受阻力显著减小,侵彻动能衰减缓慢,弹靶作用时间延长。由侵彻深度时间变化曲线可以看出,侵彻阻力的减小使得弹体的侵彻历程增加,侵彻深度提高。在(630±10) m/s和(800±10) m/s两速度段上,头部非对称刻槽弹体理论计算侵彻深度相对尖卵形弹体提高率分别为10.7%和14.1%. 通过分析头部非对称刻槽弹体的侵彻过程参量可知,头部非对称刻槽弹体侵彻过程前期阻力减小主要由弹体头部锐化作用引起,侵彻中后段弹体减阻主导因素为剪切效应引起的靶体材料强度弱化。 基于弹体压剪破坏混凝土思想,本文提出一种侵彻过程中可剪切破坏混凝土的头部非对称刻槽弹体。基于头部非对称刻槽弹体几何结构特征,提出极坐标下的头部非对称刻槽弹体结构数学表征。利用准静态柱形空腔膨胀模型,引入剪切作用下的靶体受力状态,建立轴向压缩- 切向剪切联合作用下的准静态柱形空腔膨胀理论模型,推导得到考虑剪切效应的靶体响应力函数。在此基础上,提出头部非对称刻槽弹体侵彻半无限厚混凝土目标侵彻深度局部相互作用模型。同时,开展了中低速度范围的头部非对称刻槽弹体侵彻半无限混凝土目标系列试验研究。在试验侵彻深度验证的理论模型基础上,进行头部非对称刻槽弹体侵彻过程分析。 分析结果表明,弹体头部结构改变增加了弹体头部锐度,同时引起了弹体自旋加速破坏混凝土,减小了弹体侵彻过程阻力,进而提高了侵彻深度。在考虑剪切效应的空腔膨胀模型确定靶体响应力基础上,利用局部相互作用模型可有效预测头部非对称刻槽弹体的侵彻深度,头部非对称刻槽弹体侵彻半无限混凝土目标理论模型具有较好的预测性及通用性,可用于预测头部非对称刻槽弹体结构及相应的优化设计。与尖卵形弹体相比,头部非对称刻槽弹体具有更优异的侵彻能力。1.2 弹体压剪作用下的靶体响应力模型
1.3 头部非对称刻槽弹体侵彻动力学模型

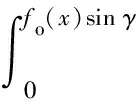
2 头部非对称刻槽弹体侵彻砂浆混凝土目标试验研究
2.1 侵彻试验方案及结果
2.2 头部非对称刻槽弹体侵彻深度理论与试验对比
2.3 头部非对称刻槽弹体侵彻过程理论分析
3 结论
