时滞类Lorenz系统的Hopf分支

李文娟，牛潇萌

（赤峰学院 数学与统计学院，内蒙古 赤峰 024000）

1 引言

近几十年来,类洛伦茨系统的研究进展迅速,大量的类洛伦茨模型被学者提出并研究.类洛伦茨系统的研究在许多方面取得了重要的成果[1-7].

1963年美国著名气象学家洛伦茨在研究区域小气候时,提出了第一个经典的洛伦茨系统

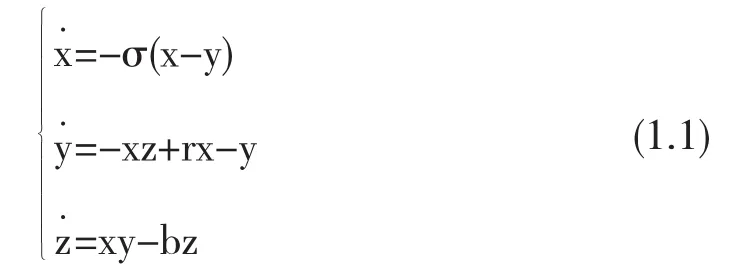
此系统在混沌学历史上有着重要的地位.

2008年Mello等提出了一类洛伦茨系统

其中x,y,z状态变量，a,b,c,d为系统参数.该系统仅有两个非齐次项，与其他系统相比，形式更加简洁所以电路便于实现，故其应用价值较大.2015官国荣等提出了一类洛伦茨系统

其中x,y,z状态变量，a,b,c,d为系统参数.此系统是将Tee系统中第一项增加了一个控制参数,第三个非线性方程中xy改为x2.因时滞现象在各系统中普遍存在,基于此,2017年李文娟等提出了带时滞的类洛伦茨系统

其中 x,y,z状态变量，a,b,c,d为系统参数,τ＞0为系统时滞.

本文的主要结果是将文献[2]的系统(1.1)中第一项增加了一个控制参数,第三个非线性方程中的-cz改为-cz(t-τ)得到一类新的时滞类Lorenz系统.然后,通过对该系统在零平衡点的线性化系统的拟特征方程的根的分析给出此系统在零平衡点的稳定性问题和发生Hopf分岔的条件.

2 主要结果

本文考虑时滞类Lorenz系统

其中x,y,z状态变量,a,b,c,d为系统参数,τ＞0为系统时滞. 设系统参数 a＞0,b＜0,c＞0,d＞0,e＞0. 系统(2.1)的平衡点满足下式：

由(2.2)式知系统(2.1)的平衡点有三个，O(0,0,0)为其中一个.

在平衡点O(0,0,0)处易求得线性化系统

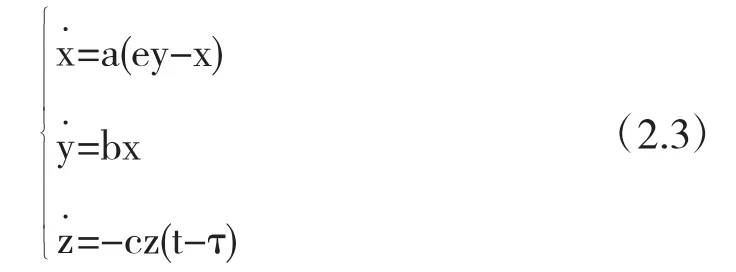
线性化系统（2.3）对应的特征方程为

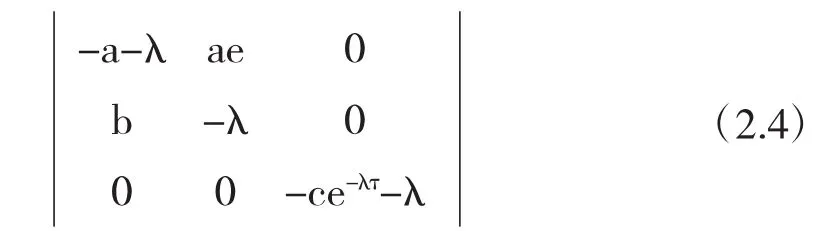
行列式(2.4)可化为

其中p1=a,p2=-abe,q1=c,q2=ac,q3=-abce.

引理1假设τ=0则系统 (2.1)在平衡点O(0,0,0)处是渐近稳定的.

证当 τ=0时，式(2.5)转化为

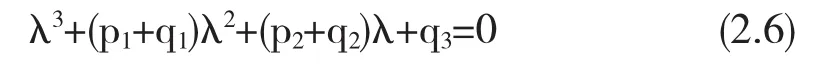
因 为 系 统 参 数 a＞0,b＜0,c＞0,d＞0,e＞0, 所 以p1+q1=0,q3＞0 且有

根据罗斯—霍维兹(Routh-Hurwitz)判据可知,式(2.6)的所有特征根都具有负实部.所以当τ=0时,系统(2.1)在平衡点O(0,0,0)处是局部渐近稳定的.

当 τ＞0时,设 λ=iω（ω 是大于零的常数）是式(2.5)的一个纯虚根,则虚部ω满足

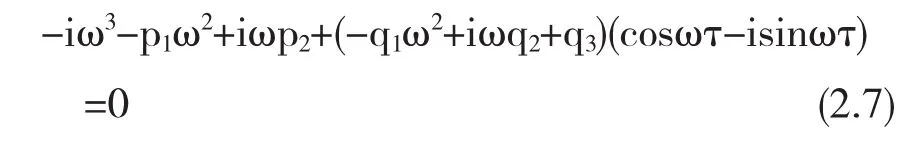
根据复数相等可得

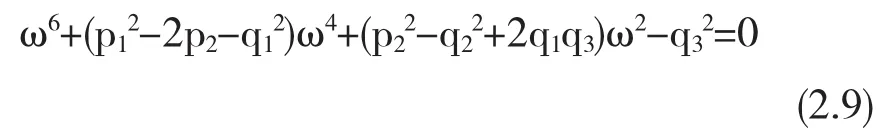
对(2.9)式有以下结论.

引理2式(2.9)至少有一个正实根.

证令u=ω2,则式(2.9)可化为

函数（2.11）可化为

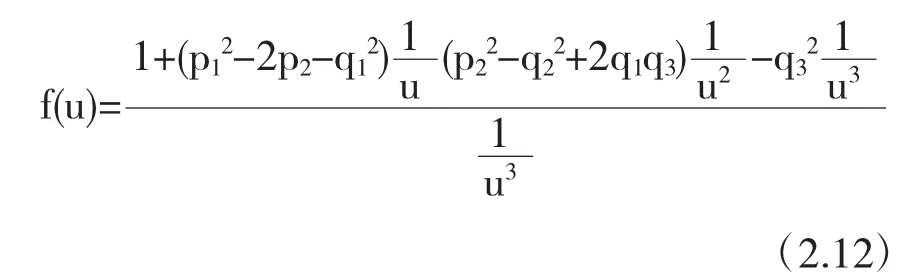
由（2.11）和（2.12）式得

根据函数零点存在定理,至少存在一个实数u0∈(0,+∞),使得 f(u0)=0.所以式(2.10)至少有一个正实根.因为u=ω2，从而式（2.9）至少有一个正实根.

设 ω0为式（2.9）的正实根，则式(2.5)有一纯虚根 iω0.又由式（2.8）得

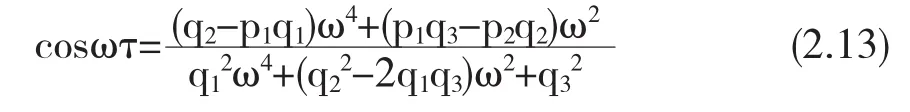
将ω=ω0代入方程(2.13),则时滞τ的值为

第三，可以考虑在中学和初级学院的华文文学课程中融入比较文学的理论和方法，指导学生在比较文学的视域中，了解本地文学、中国文学和世界文学。

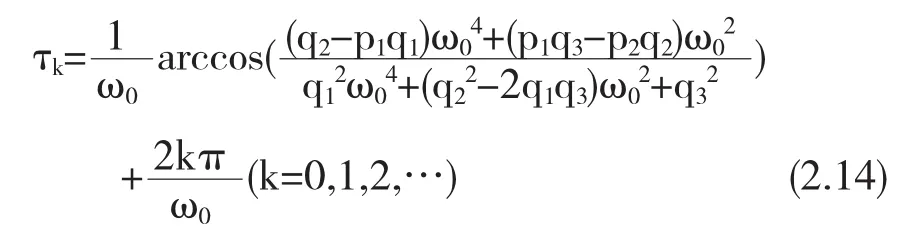
因此(ω0,τk)是式(2.5)的解,即当时滞 τ=τk时,λ=±iω0是式(2.5)的一对共轭的纯虚根.

设 τ0=min{τk},则时滞 τ=τ0是式(2.5)出现纯虚根λ=±iω0时 τ的最小值.

引理 3如果 a＞0,b＜0,c＞0,d＞0,e＞0,τ=τ0, 那么式(2.5)有一对纯虚根 λ=±iω0.

设式(2.5)的特征根 λ(τ)=iω(τ),满足 ω(τk)=ω0.

引理 4如果 f'(ω02)＞0 则

证对式(2.5)的两边关于τ求导可得

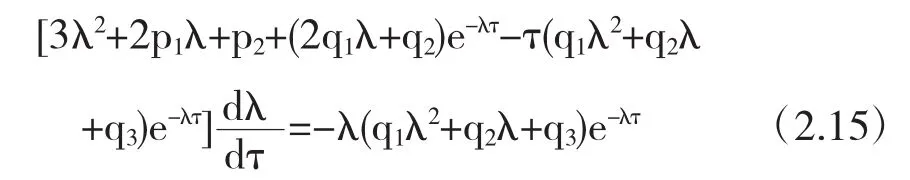
由式(2.5)可得

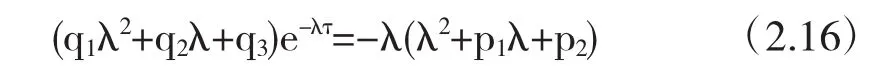
将式（2.16）代入式(2.15)可得

由(2.17)式和 λ(τk)=iω0,可得

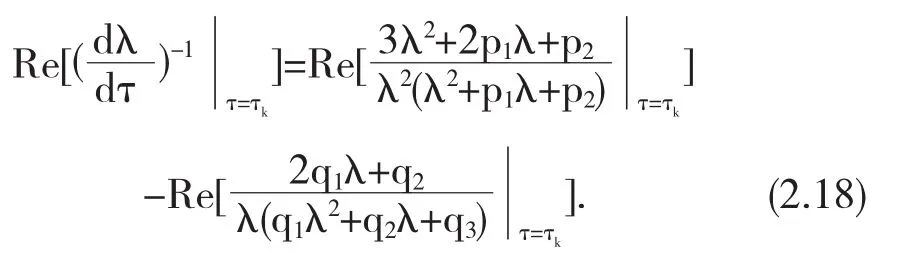
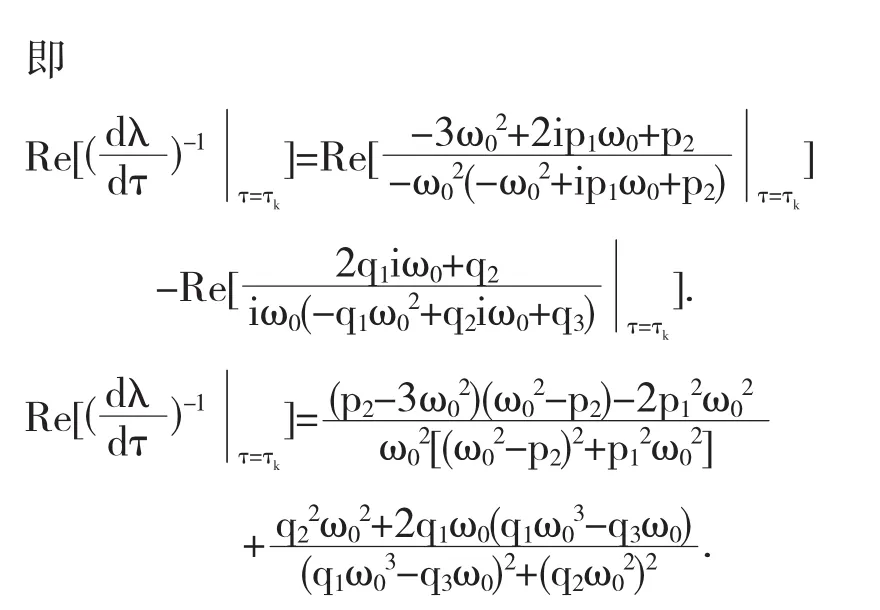
将 λ(τk)=iω0代入式(2.5)可得

由(2.19)式可得

由(2.19)式和(2.20)式可得

根据引理4和Hopf分岔理论可得下面结论．

定理如果 a＞0,b＜0,c＞0,d＞0,e＞0 且 f'(ω02)＞0，那么

（1）当 τ∈[0,τ0]时，系统(2.1)在平衡点 O(0,0,0)是渐近稳定的；

（2）当 τ＞τ0时，系统(2.1)在平衡点 O(0,0,0)是不稳定的；

（3）当 τ=τk(k=0,1,2,…)时，系统(2.1)在平衡点 O(0,0,0)处发生Hopf分支，产生极限环.

3 数值仿真

时滞类Lorenz系统 (2.1)的参数a＞0,b＜0,c＞0,d＞0,e＞0，令 a=10,b=-8,c=2.5,d=4,e=1，这时系统(2.1)可化为

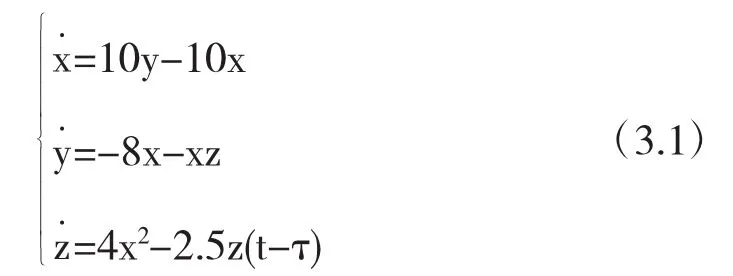
利用Matlab软件计算得式（2.9）的正实根ω0=6.6588，f'(ω02)＜0，式（2.13）中 τ0=0.0738.

推论若a=10,b=-8,c=2.5,d=4,e=1，则

（1）当 τ∈[0,0.0738]时，系统(3.1)在平衡点 O(0,0,0)是局部渐近稳定的；

（2）当 τ＞0,0738 时，系统(3.1)在平衡点 O(0,0,0)是不稳定的；

（3）当 τ=0.0738+0.1502kπ(k=0,1,2,…)时，系统(3.1)在平衡点O(0,0,0)处发生Hopf分岔，产生极限环.