面向文件存储的虚拟网络映射算法

陈 晨，郑 烇，王志臻，田洪亮

(1. 中国科学技术大学 信息科学技术学院，安徽 合肥 230027； 2. 中兴通讯股份有限公司，广东 深圳 518057)

0 引言

随着网络技术的发展，为了解决当前互联网“僵化”问题，研究者提出了网络虚拟化技术，它可以为用户提供多样化服务[1-2]，也是构建新一代网络体系架构的重要支撑[3]。虚拟网络映射是实现网络虚拟化的关键环节，其目的是在满足虚拟网络请求(Virtual Network Request, VN请求)的前提下，将虚拟网络以最小化成本映射到物理网络上，实现网络资源的高效利用[4]。

虚拟网络映射问题包括节点映射和链路映射两个问题，一般在节点映射阶段采用启发式算法，然后在确定源和目的节点的基础上，将链路映射转化为最小费用流问题，采用最短路径算法完成映射。根据两个问题是否独立进行，可将虚拟网络映射分为同阶段映射和两阶段映射[5]。同阶段映射中，在映射虚拟节点的同时考虑链路映射，如D-ViNE算法[6]和vnmFlib算法[7]。两阶段映射中，节点映射和链路映射独立进行，先映射节点后映射链路，如NA-PVNM算法[8]。

在已有的研究中，VN请求大都是对节点计算资源和链路带宽资源的需求。本文研究的是将含有文件需求的VN请求映射到有存储的物理网络上，VN请求不仅包括以上的需求，还包括对节点存储资源的需求。因为物理节点上可能存在请求文件的存储，所以当请求命中时，该节点流向下游的流量减少。该情况可以转化为节点的损耗问题，即广义最小费用流问题[9]。本文提出了一种基于节点连通性和广义网络单纯形法的虚拟网络映射算法——S-VNM算法，在节点映射阶段综合考虑节点位置和链路映射的映射成本两个因素，从而减小搜索空间，降低映射成本。通过实验仿真验证了该算法的有效性和良好性能。

1 相关技术

1.1 虚拟网络映射问题描述

1.1.1虚拟网络映射模型

在虚拟网络映射模型中[10]，物理网络由一个无向图GS=(NS,ES,CS,BS) 表示，其中NS代表物理节点，ES代表物理链路，CS代表物理节点的资源，BS代表物理链路的资源。本文研究的是在有存储的物理网络上进行虚拟网络映射，因此，CS代表的节点资源包括节点计算资源和存储资源。VN请求也可以表示为GV=(NV,EV,CV,BV) ,各字符代表的意义与物理网络类似。虚拟网络映射过程用映射函数M(GV,GS)来表示：

M(GV,GS) :

(NV,EV,CV,BV) →(NS,ES,CS,BS)

(1)

1.1.2约束条件

虚拟节点映射时要满足物理节点不可分拆、计算资源及存储资源的约束，表示如下：

M(i) ≠M(j), ∀i,j∈NV且i≠j

(2)

CSC(M(nV))≥CVC(nV), ∀nV∈NV

(3)

CSS(M(nV))≥CVS(nV), ∀nV∈NV

(4)

其中，式(2)表示每个虚拟节点只能映射到单个且互不相同的物理节点上；式(3)和式(4)分别表示物理节点可用的计算资源和存储资源不少于虚拟节点的所需。

定义虚拟链路lV=(i,j) 映射到物理链路上的路径集合为PM(lV) 。定义路径p∈PM(lV) 上为虚拟链路分配的带宽为B(lV,p)。虚拟链路映射时约束如下：

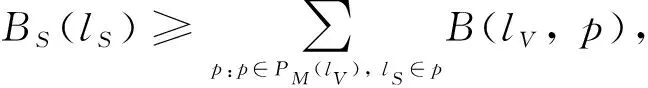
(5)

式(5)表示链路映射过程中物理链路lS上有足够的带宽资源BS(lS)。

1.1.3性能指标

虚拟网络映射问题是节点和链路资源约束下的优化问题，主要的性能指标有映射成本、映射时间[11]及VN请求的接受率等。本文以映射成本和映射时间作为评价算法的性能指标。

虚拟网络的映射成本包括节点映射成本和链路映射成本。总映射成本C(GV) 表示如下：

(6)

其中，CNC(nV) 代表节点映射的计算成本，CNS(nV) 代表节点映射的存储成本，CE(lV) 代表链路映射成本。

1.2 广义最小费用流问题描述

在一些实际的网络流问题中，有些节点和弧并不满足流量平衡条件，使得经典的网络模型无法对其描述，现有研究将其称为广义费用流问题[9]。

1.2.1广义最小费用流问题

令G=(N,A) 为一个有向网络，其中N为节点的集合，A为弧的集合。对于任意的弧 (i,j)∈A，令xij表示从节点i出发沿着弧 (i,j) 行进的流量，uij为xij的上界，即：

0 ≤xij≤uij,(i,j)∈A

(7)

令 0<μij<1 为弧 (i,j) 上的损耗因子，并假设当沿着弧 (i,j) 从节点i发送一个单位流量时，有μij个单位流量到达节点j。对于节点i∈N，定义E(i)和L(i) 分别为“进入”和“离开”该节点的弧的集合，即：

E(i)={(j,i)∈A:j∈N} 且

L(i)={(i,j)∈A:j∈N}

(8)

1.2.2各节点约束条件

对于源节点S-节点，令NS表示所有S-节点的集合。对每一个i∈NS，有E(i)=φ，且有一个输入流xi使得：

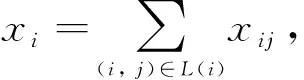
(9)

对于转运节点O-节点，满足：

(10)

对于分配节点D-节点，输出弧上的流量与进入弧上的流量成比例，满足：

(11)

对于目的节点T-节点，对每一个i∈NT，有L(i)=φ，且有一个输出流xi使得：

(12)

2 本文算法

本节详细介绍了S-VNM算法，该算法实现了将含有文件需求的VN请求映射到有存储的物理网络上。其分为三个阶段：(1) 虚拟节点排序；(2) 虚拟节点映射；(3) 虚拟链路映射。

2.1 虚拟节点排序

一个具体的VN请求包含多个虚拟节点，由于物理网络资源有限，对资源需求越大的节点越难映射成功，因此优先映射该类节点。同时，为了保证映射的相关性，在进行下一个虚拟节点映射时，优先选择与已映射的虚拟节点集合有关联的节点。

定义虚拟节点的需求CR(nV) 如下：

(13)

其中，CC(nV) 代表虚拟节点nV的计算资源需求，CS(nV) 代表nV的存储资源需求，L(nV)代表所有与nV相关联的链路集合，B(l) 代表与nV相关联的链路所需的带宽资源。

2.2 虚拟节点映射

本文提出的虚拟节点映射算法是基于物理节点连通性和映射总成本实现的。

定义与虚拟节点nV相关联的已映射虚拟节点在物理网络中的映射节点集合为M。定义物理节点ns与集合M的连通性为Nrank(ns)：

Nrank(ns)=

(14)

其中，CC(ns) 代表物理节点ns的可用计算资源，CS(ns) 代表ns的可用存储资源，Cavailable(nt,ns) 代表物理节点nt与ns之间的可行流，D(nt,ns) 代表两节点之间的距离。

按照节点连通性将物理节点由大到小排序后，选择排序靠前的节点作为待选节点。然后，对待选节点进行节点映射和链路映射，根据每一次映射结果，统计节点的映射成本和所有相关链路的映射成本作为效用函数Ctotal(ns)，以此来评价物理节点ns，最终选择效用函数最小的节点作为映射节点。效用函数Ctotal(ns) 表示如下：

(15)

其中，CNC(nV) 代表节点映射的计算成本，CNS(nV) 代表节点映射的存储成本，CE(nt,ns) 代表映射到物理节点ns的最小链路映射成本。

2.3 虚拟链路映射

在虚拟节点映射时，节点映射成本易求出，但如何求最小链路映射成本的问题可转化为最小费用流问题。

本文的VN请求含有文件需求，因此在映射的过程中，应考虑该情况：如果当下的映射节点与已映射节点之间的路径上存在含有该文件的节点，当请求命中时，有该文件的节点类似于分配节点D-节点，需留下该文件的流而将其他需求的流送出。由此可见，求解链路映射成本问题可转化为广义最小费用流问题。

虚拟链路映射成本问题的模型可以表示为：

(16)

s.t.x∈F

其中，x是在给定网络G=(N,A) 的弧集上的可行流，F是所有满足式(7)～(12)的可行流的集合，Cij是从节点i出发的单位流量沿弧 (i,j) 到达节点j所产生的费用。

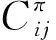
(17)

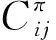
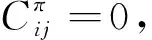
(18)

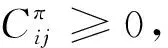
(19)

则 (F,L) 为最优结构。

本文提出的虚拟链路映射算法的核心思想是：

(1) 生成初始基本可行结构 (F,L)。

(3) 检验式(19)和式(20)所示的最优条件。如果所有的最优性条件全都满足，则算法停止；否则，选择一条不满足最优性条件的弧 (k,l) 作为进基弧。

(4) 在进基弧 (k,l) 上增加适当的流量，计算基本可行图上各弧上流量的调整量，更新基本可行解x和基本可行结构 (F,L)，转步骤(2)。

由此，可求出基本可行解x，进而计算出虚拟链路映射的最小成本，再计算出待选节点的效用函数Ctotal(ns)，选择该值最小的节点作为映射节点，最终完成虚拟网络映射。

算法S-NVM

输入：VN请求(NV,EV)，物理网络(NS,ES)；

输出：虚拟映射M(GV,GS)。

1.M=φ，Di=φ，i=0，step=0，N

// 初始化

//Di代表待选物理节点的集合

2. for allnV∈NV

//虚拟节点排序

3. count theCR(nV) ofnV

4. end for

5. arrangenVin descending according toCR(nV)

7. if (M=φ)

// 第一个虚拟节点映射

11. end if

12. else

// 虚拟节点和虚拟链路映射

// 选择与上一个映射的虚拟节点有关联的节点

// 选择按照连通性大小排序后的前N个节点

17. step++

19. end for

23. end else

24.i++

25. end for

3 实验与结果分析

实验通过MATLAB进行仿真评估。采用GT-ITM拓扑产生器随机生成物理网络和虚拟网络请求。本文将D-ViNE算法和vnmFlib simple算法作为对照，从映射成本和算法运行时间两方面进行比较。

物理网络包含60个节点，150条链路。物理节点的可用计算和存储容量服从[50,150]均匀分布，单位成本服从[1,5]均匀分布。物理链路可用带宽容量服从[1,100]均匀分布，单位成本服从[1,10]分布。虚拟网络节点个数服从[3,15]均匀分布，任意两个虚拟节点之间以0.5的概率连接，虚拟节点和虚拟链路需求服从[10,50]均匀分布。μij=0.7。

基于以上仿真环境，运行三种映射算法，结果如图1和图2所示。

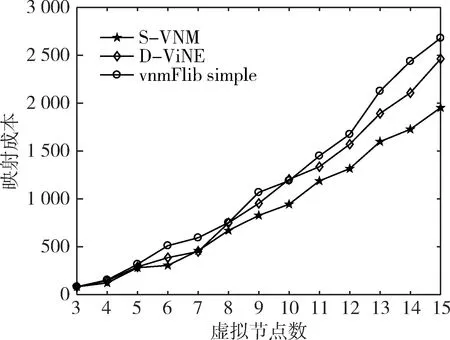
图1 映射成本随虚拟节点数变化趋势图

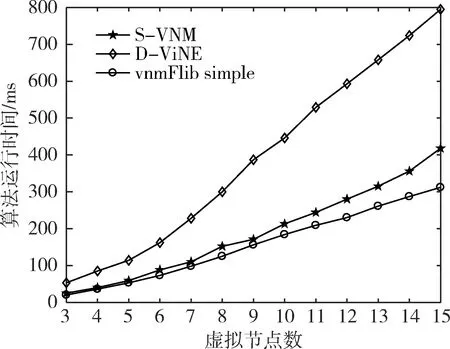
图2 算法运行时间随虚拟节点数变化趋势图

实验结果表明，S-VNM算法整体上比其他两种算法有优势。在映射成本方面，S-VNM算法性能最好，因为在搜索解空间过程中每次都取映射成本最小的节点作为映射结果。在运行时间方面，S-VNM算法优于D-ViNE算法，这是因为S-VNM算法在映射时选择连通性较大的节点进行映射，减小搜索空间，从而降低运行时间。但S-VNM在运行时间方面劣于vnmFlib simple算法，这是因为vnmFlib simple算法直接使用区间内的最大跳数作为路径条数约束，虽没有减小搜索空间，但算法复杂度低，所以运行时间短。

4 结论

本文提出一种启发式搜索和基于广义网络单纯形法的虚拟网络映射算法——S-VNM算法，其实现了将含有文件需求的VN请求映射到有存储的物理网络上。S-VNM算法在节点映射阶段把物理节点之间的连通性作为筛选标准，虚拟节点的映射成本作为效用函数，与传统算法相比减小了搜索空间，降低了映射成本。在链路映射阶段采用广义网络单纯形法，与最短路径算法相比降低了映射的时间复杂度。实验结果表明，在综合考虑映射成本和算法运行时间的情况下，本文提出的算法性能最优。