石墨烯中自旋过滤态和量子自旋霍尔效应

杨 圆,李小兵,林季资

(1.江苏科技大学 张家港校区 基础教学部，张家港 215600) (2.南京大学 固体微结构物理国家重点实验室，南京 210093)

拓扑绝缘体是最近几年发现的一种全新的物质形态,其体电子态是有能隙的绝缘态,而其表面或边缘是无能隙的金属态[1-3]．这种金属态完全由体能带的拓扑性质所决定,受时间反演对称性的保护,可以避免非磁性杂质散射．文献[4]中首次在石墨烯中提出了一种受到时间反演对称性保护的二维拓扑绝缘体,即量子自旋霍尔效应．文献[5]中提出在HgTe量子阱中可能观察到这种效应,并被随后的实验工作证实[6]．量子自旋霍尔体系的重要特征是具有比较强的自旋轨道耦合,在样品的边界,自旋向上的电子和自旋向下的电子沿着相反的方向传播,它们可以传导自旋流但不导致能量耗散．

量子自旋霍尔体系的拓扑不变量可以由Z2拓扑数[7]或者自旋陈数[8-9]来定义．Z2指标不适用于时间反演对称破缺的体系,因为它的定义依赖于时间反演对称性的存在．相反,自旋陈数在时间反演对称破缺的体系中也是有效的．近年来,自旋陈数的方法被应用于描述交换场作用下量子自旋霍尔体系的拓扑性质[10-11],研究结果发现,在时间反演对称性被破坏后,量子自旋霍尔相依然存在．目前也有实验表明,量子自旋霍尔效应在没有时间反演对称性的情况下可以是稳定的[12]．

文中以石墨烯中的量子自旋霍尔效应为基础,引入破坏时间反演对称性的非均匀交错磁场,研究量子自旋霍尔体系在交错磁场和交换场作用下的拓扑相变,利用陈数和自旋陈数对系统中的非平庸拓扑相进行分类,并观察边缘态的性质．

1 模型与方法

1.1 紧束缚模型

石墨烯在非均匀的垂直磁场作用下,其紧束缚模型哈密顿量可以写为[4,9-11]

(1)

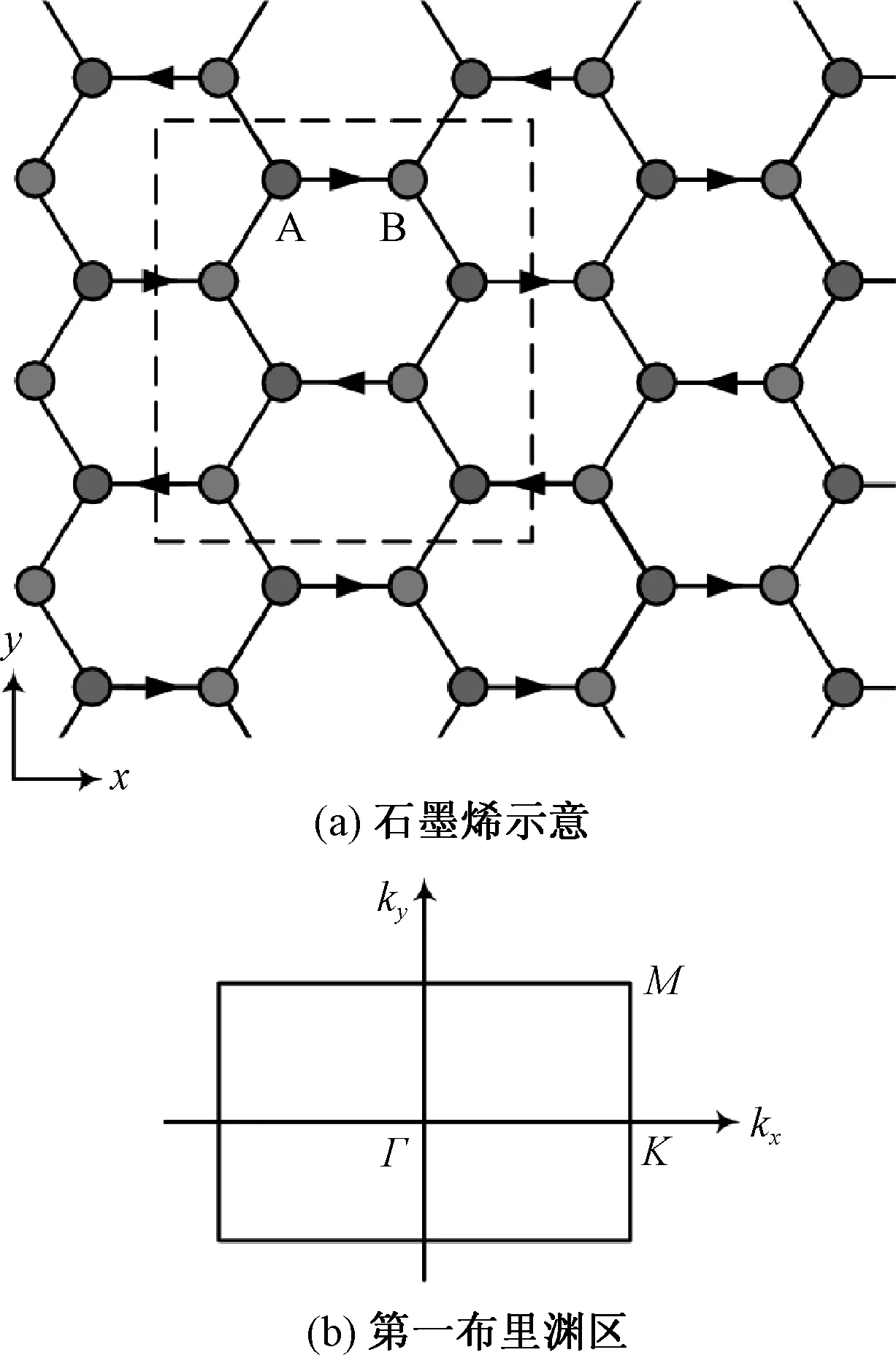
图1 交错磁场下的石墨烯Fig.1 Graphene under a staggered magnetic field

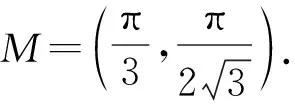
1.2 自旋陈数与边缘态

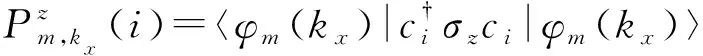
2 数值结果与分析

2.1 时间反演对称破缺的量子自旋霍尔相

取参数λso=0.1,石墨烯系统处于时间反演对称的量子自旋霍尔态．加入破坏时间反演对称性的交错磁场(图1(a)),讨论量子自旋霍尔态在时间反演对称性被破坏情况下其边缘态的相关性质．

图2(a～c)为3个不同的磁场强度得到的边缘态能谱．给定费米能量EF=0.1t,当φ=π/4时,如图2(a),在边缘上出现无能隙边缘模式．这里共有4个不同的边缘态,分别标记为A,B,C,D．通过分析波函数的空间分布,发现边缘态A和B局域在样品的一个边界,C和D局域在另一个边界．以A和B两个态为例进行研究,从A和B点所在的色散曲线的斜率很容易看出这两个边缘态沿着相反的方向运动,通过计算这两个态的自旋极化,点A的态自旋向下,点B的态自旋向上．在样品的一个边界上,自旋极化相反的两个边缘态沿着相反的方向运动,这与计算所得的陈数C=0和自旋陈数Cs=1相对应,因此量子自旋霍尔态的非平庸拓扑性质可以在时间反演对称破缺的体系中存在．

边缘态随着φ的变化而演化的过程如图2(b)、2(c),这两个体系展现同样的量子自旋霍尔效应．一个显著的区别是,在φ=π时,C=0、Cs=2,即在样品的每个边界上存在着两对反向传播的具有相反自旋极化的边缘态,如图2(d)．如果费米能量处于EF=±1.75t,体系依然处于量子自旋霍尔态,如图2(b)和2(c),图2(c)中处于EF=1.75t上的边缘态E和G以及边缘态F和H对应陈数C=0,而自旋陈数Cs=1．

通过调节交错磁场的强度和石墨烯的费米能级,具有不同自旋陈数的量子自旋霍尔相之间可以发生拓扑相变．更为重要的是,无能隙的边缘态可以在时间反演对称破缺的量子自旋霍尔体系中出现．

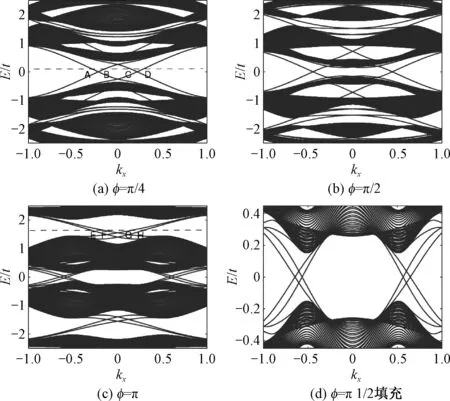
图2 当λso=0.1时不同φ值下的能谱Fig.2 Energy spectrum at λso=0.1 with different values of φ

2.2 自旋过滤的量子霍尔相

取参数λso=0.1,λR=0.1,φ=π,这样确保了不考虑交换场的情况下,体系处于时间反演对称破缺的量子自旋霍尔态．图3(a～c)展示了对应于3个不同交换场强度得到的能谱．当g=0.3时,对应一个给定的费米能量EF=0.02t,共有8个不同的边缘态,分别标记为A,B,C,D,E,F,G,H,如图3(a)．可以看出A,C,E和G局域在一个边界上,沿着-x方向运动,而B,D,F和H局域在另一个边界上,沿着x方向运动,对应量子霍尔相,陈数C=-4,而自旋陈数Cs=0．当g增大时,陈数C=-2,体系仍然是一个量子霍尔相,在样品的一个边界上共有两个边缘态沿着同一方向传播,边缘态如图3(b)．进一步增大交换场到g=1.5时,C=0、Cs=-1,体系处于量子自旋霍尔态,在样品的一个边缘上自旋相反极化的两个边缘态沿着相反的方向运动(图3(d))，并且可以发现边缘态能谱中存在着能隙．特别当EF=1.6t时,在样品的每个边缘上只有两条自旋向上的边缘态沿着相同方向传播,对应陈数C=2，这意味着石墨烯系统处于自旋过滤的量子霍尔态．类似的,当EF=3.25t时,C=1，只有一条自旋向上的边缘态出现在样品的每个边界上．相反,在EF=-1.6t或者EF=-3.25t时,只有自旋向下的边缘态存在,如图3(c)．

前面的讨论已经证明,量子自旋霍尔体系的非平庸拓扑性质在时间反演对称破缺后仍然可以存在．将图2(d)、3(d)的1/2电子填充时的量子自旋霍尔态相比较,可以看出在边缘上发生两种情况：① 在边缘出现无能隙边缘模式；② 边缘态能隙打开,导致有能隙的边缘态．计算投影自旋算符PσzP的能谱,投影自旋算符的矩阵元为〈φm(kx)|σz|φn(kx)〉,m和n遍历所有被电子占据的态．通过对该矩阵对角化,可以得到投影自旋算符PσzP的能谱．对应于图2(d)、3(d)中给定的参数,计算获得的自旋谱Es,如图4(a)、4(b)．对于无能隙的边缘态,自旋谱展现出很大的谱隙,只有两个值±1,如图4(a)．当边缘态能谱存在能隙时,自旋谱随着kx增加,从-1到+1连续变化,没有出现任何谱隙．图4展示的结果验证了只要体系处于量子自旋霍尔态,边缘能谱或者自旋谱两者之一必然表现出无谱隙的特征[14]．

图3 当λso=0.1,λR=0.1,φ=π时,不同g值下的能谱Fig.3 Energy spectrum at λso=0.1, λR=0.1, φ=π with different values of g

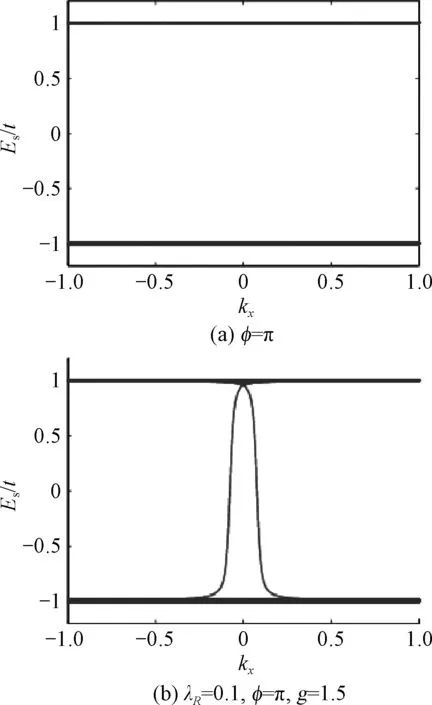
图4 当λso=0.1时量子自旋霍尔态的自旋谱Fig.4 Spin spectrum of quantum spin Hall states at λso=0.1

3 结论

文中研究了石墨烯系统在交错磁场和交换场作用下的拓扑相变．通过调节交错磁场强度和石墨烯的费米能量,系统中出现许多拓扑相,包括具有高自旋陈数Cs=2的量子自旋霍尔相和高陈数C=-4的量子霍尔相．重要的是,无能隙的边缘态可以在时间反演对称破缺的量子自旋霍尔体系中出现．引入一个交换场,调节交换场的大小,系统发生了从时间反演对称破缺的量子自旋霍尔态到自旋过滤的量子霍尔态的相变．边缘态性质和基于陈数和自旋陈数的拓扑刻画完全一致．