地铁运营突发事故风险传播规律研究*
2018-08-06陈文瑛杨金谕何世伟
陈文瑛,杨金谕,何世伟
(1.首都经济贸易大学 安全与环境工程学院,北京 100071;2.城市群系统演化与可持续发展的决策模拟研究北京市重点实验室,北京 100071;3. 北京交通大学 交通运输学院,北京 100044)
0 引言
地铁以其快速、准时、便捷等突出特点,已成为各大城市居民日常出行的重要交通工具。然而,地铁大多建设于地下,线路单一、空间封闭,一旦单点发生运营突发事故,事故风险会迅速扩散至整条线路。在地铁网络化条件下甚至会通过换乘站扩散至其他路线,进而影响整个路网的安全有效运营。
目前,国内外关于地铁事故风险传播的相关研究主要集中于地铁交通网络可靠性及抗毁性[1-2]和地铁大客流风险传播两方面。交通网络连通可靠性反映的是交通网络节点之间保持连通的概率,最早由日本的Main和Kawai[3]于1982年提出;在此基础上,1997年Bell和Iida[4]在《Transportation Network Analysis》一书中首次详细描述了其定义及求解算法;谭跃进等[5]最早开始从抗毁性分析和抗毁性优化两个方面详细论述目前国内外复杂网络抗毁性研究的进展;邓旭东等[6]从突发事故后能相互到达的站点数、破坏站点会对整条线路带来的影响两个角度,构建了地铁网络脆弱性评价模型;许葭等[7]提出了地铁网络事故蔓延引力模型,并通过北京地铁网络验证了模型的有效性。此类研究多是基于复杂网络理论,将地铁网络抽象成无权无向图,从网络物理拓扑结构层面进行分析,研究过程中更注重于静态网络结构,而很少考虑风险载体——“客流”这一动态因素在地铁网络风险传播中的作用。对于地铁大客流风险传播方面的研究,李冰玉等[8]通过建立基于客流实时分布的拥堵传播模型,得到了大客流拥堵传播与发生拥堵车站的结构特性有关的结论;朱自刚等[9]对列车延误影响的路网客流分布特性进行了研究,提出了关于列车延误对客流疏散影响的指标;彭其渊等[10]定量分析了突发大客流对于换乘站服务水平和列车运行影响;李凌燕[11]、牛龙飞[12]、李朴[13]均是通过构建SIR传播模型来分析大客流的传播特性。这类论文关注点主要是常规通勤大客流或由大型活动引起的突发大客流(外部客流)在路网中的传播以及影响规律,而对于地铁运营过程中突发事故引起的大客流(内部客流)在网络中的传播问题则研究较少。
然而,地铁运营突发事故风险的传播不只受到地铁网络结构或客流传播单方面影响,而与两者均有关系。因此,本文综合考虑静态的地铁网络结构与动态的客流传播,分析和讨论运营突发事故风险在地铁单线路及换乘站的传播规律,为后续研究事故风险在路网中的传播规律奠定基础。
1 单线路地铁运营突发事故风险传播
1.1 风险分析
随着智能化的逐步提升,未来地铁的运营模式趋于全自动无人驾驶。在这种驾驶模式下,当线路上运行的某列地铁因突发事故(如设备故障)而停止运行时,其后续列车会在列车自动防护系统ATP(Automatic Train Protection)的作用下开始制动降速,随后相继停车,甚至造成线路的停运。
地铁线路按形状可分为环形和非环形2种。环形线路中单向线路的停运不会给对向列车运营造成直接影响,但会带来大客流冲击,引发大客流风险;非环形线路中,由于列车会在末站进行折返作业后进入对向线路继续运营,形成1条闭合环形线路,因此,单向线路的停运会导致对向折返列车无法正常进线运营,从而逐渐逼停上下行线路的所有列车。
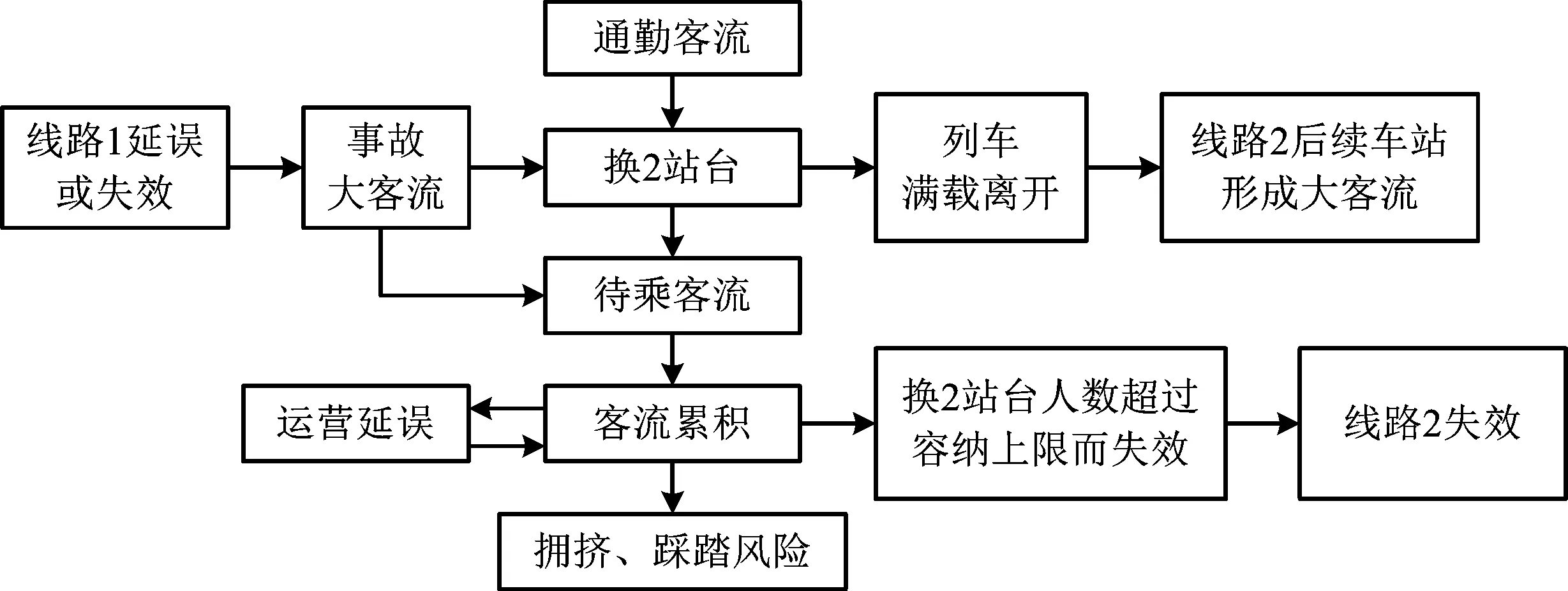
地铁线路的单一性会导致停运列车中的乘客滞留区间,如果事故不能短时间解决,就会给区间中乘客的人身安全带来威胁。同时,线路的失效会造成该线路各站台乘客集聚甚至达到站台可容纳人数的极限值,极易造成乘客恐慌、拥挤踩踏等事故。单线路地铁运营突发事故风险传播路径如图1所示。

图1 单线路地铁运营突发事故风险传播Fig.1 Risk transmission of subway operation sudden incident in single line
1.2 模型构建
为分析和定量计算突发事故对单线路地铁运营造成的影响,作出如下假设:①线路上各列车追踪距离相同;②列车均为全自动驾驶模式、移动闭塞;③由于列车加减速行驶时间较短,认为列车在线路上连续匀速运行,忽略加减速等情况;④车站运营组织未采取相关应急措施。
1.2.1 参数定义
以下参数在后文中代表的含义为:L为线路总长度,m;bj为线路上第j列车(j=1,2,…,m),发生突发事故的列车定为b1;ai为线路上第i个车站,列车b1停车所在的车站或即将到达的车站定为a1;li为车站ai与车站ai+1的间距(i=1,2,…,n),m;T为突发事故持续时间,s。
1.2.2 模型构建
1)停运列车数量确定
①线路占用率
将线路上实际运营的列车数量与最大可运营列车数量的比值定义为线路占用率,用H表示[14]。
(1)
式中:m为线路上实际运营列车数量,列;mmax为线路上最大可运营列车数量,列;l为列车长度,m;s为列车正常行驶间距,m;smin为列车最小防护距离,m;tmin为列车最小追踪时间,s;t为列车正常追踪时间,s。
②缓冲时间
将发生突发事故造成某列车停车后,其后续列车从正常行驶距离至最小防护距离停车所用的时间定义为缓冲时间,用th表示。
(2)
式中:v为列车平均速度,m/s。则此处bj列车的缓冲时间为:
th,j=(j-1)·th
(3)
③停运列车数量
当tb,k (k-1)·th (4) 则事故持续时间内造成后续列车停车数量为(k-1)列,即: (5) 由以上计算可知,突发事故会造成线路上共k列车停止运行。当k≥m时,说明事故线路列车全部停运,线路失效。 2)停运列车位置确定 设b1列车停车时与a1车站的距离为X,则bj(j>1)列车在停车后,其与各个车站的距离可用|(j-1)·smin-Σli+X|表示(i=1,2,…,n),本文研究列车停靠在车站内发生事故的情况,故X=0。 (6) 式中:Wji为列车bj相对于最近车站ai的距离(j=2,3,…,k),m。 1.2.3 突发事故对单线路运营影响后果计算 突发事故对单线路运营影响除了造成该线路列车时间上的延误、停运车站乘客聚集,还会给滞留在区间中的乘客人身安全带来威胁。 1)停运列车分布 突发事故后,列车位于车站内或者是车站前后l范围内时均可顺利进行乘客疏散,故都认为站内停车;若列车位于区间中且与最近的车站的距离超过l,则为区间停车。 令D为站内停车数量,个;C为区间停车数量,个。 (7) C=k-D (8) 2)区间滞留乘客数量Nq Nq=ε·C·K (9) 式中:ε为列车满载率;K为列车核定载客数,人/列。 突发事故导致单线路的运营延误甚至失效之后,事故风险会通过换乘站进一步传播到其他线路。为方便说明,此处将突发事故线路定为线路1,通过换乘站连接的线路定为线路2,换乘站中线路1方向站台为换1站台,线路2方向站台为换2站台。 线路1运营延误或失效导致该线路上产生事故大客流,事故大客流通过换乘站传播到线路2与换乘站既有客流叠加,将导致换2站台候车区乘客迅速累积。随着客流的持续涌入,候车区乘客人数将达到容纳上限,轻则会造成线路2的运营延误,重则会由于客流过度拥挤而导致换2站台失效,进一步导致线路2的运营失效,给路网的安全有效运营、乘客的生命安全都带来严重的威胁。如2013年9月16日早高峰期间,北京地铁4号线发生自动控制系统故障,运营中断近3 h,大量乘客滞留车站,路网中其他路线也受到了不同程度的影响[13]。单线路运营中断后风险经换乘站传播情况如图2所示。 2.2.1 换乘线路运营延误 换2站台候车乘客持续增多,当候车乘客数量大于线路2到达列车的剩余载客能力时,换2站台每列到站列车都会达到最大载客量时才会出站。此时,由于上车乘客数量的增多以及车门处上下车乘客相互拥挤对上车效率产生的影响会造成乘降时间的增加,导致线路2列车在换2站台的出发延误[11]。因此,换2站台单列车的出发延误时间表示为列车实际停站乘降时间与图定停站时间的差值。此处默认列车6节编组,共24个车门。则有: 图2 单线路运营中断后风险经换乘站风险传播Fig. 2 Risk transmission of transfer station after the single line broken (10) 式中:tfy为列车在换乘站发车延误时间,s;Kmax为列车最大载客量,人/列;τ为列车通过客流所占比例;γ为平均上车效率,人/(s·门);β为上下车客流交叉影响系数,指上下车乘客由于方向冲突、相互拥挤而对上车效率造成的影响,此处取0.25;ttd为列车的图定停站时间,s。 2.2.2 客流累积 事故大客流的持续涌入及运营延误的影响,会导致换2站台滞留乘客数量急剧增多,拥挤度提高,甚至超过站台的可容纳人数上限,导致换2站台的失效。定义站台拥挤度为换2站台实际乘客数量与站台可容纳人数上限的比值,用F(Td)表示[15],其中Td为线路1总延误时间,分为初始延误时间(事故持续时间)和后续延误时间(恢复运营时间)。为便于计算,此处取Td=3T。则有: (11) 式中:Z为站台可容纳人数上限,人;φ为换2站台乘客平均到达率,人/s;N0为换2站台初始人数,人;Kmax为列车最大载客量,人/列;t为列车正常追踪时间,s。 以北京地铁2号线及复兴门换乘站为例,对单线路及换乘站风险传播模型进行实例计算与分析。 计算中使用的各参数值如表1~2所示。 表1 北京地铁2号线基本参数Table 1 Parameters of Line 2 of Beijing subway 注:参数来源于北京地铁官方网站及北京地铁运营公司客流统计。 表2 其他参数Table 2 Other parameters 注:参数主要来源于复兴门站台实测。 3.2.1 突发事故对单线路运营影响计算 不同事故持续时间对运营的影响结果如表3所示,图3为不同事故持续时间对应的线路占用率与停运列车数量关系图。 由表3可知,事故持续时间与线路停运列车数基本符合正相关线性关系。随着事故持续时间的增加,停运列车数量增多,同时停靠在区间中的列车数量所占比例也不断增大,说明事故持续时间越长,列车停靠区间的概率越大。事故持续时间继续增大到一定值时,停运列车数量不再增长,说明此时线路上所有车辆均被逼停,线路运营失效。 表3 不同事故持续时间对运营的影响Table 3 The influence of different accident duration to metro operation 图3为不同事故下线路占用率和停运列车数量的关系,由图3可以看出,线路占用率较低时,突发事故造成的停车数量较少且增速缓慢。当线路占用率达到60%左右时,突发事故造成的停车数量会开始快速增长。同时,事故持续时间越长,突发事故造成的停车数量增速越快,事故风险越大。 图3 不同事故持续时间T对应的H-kFig.3 The “H-k”chart corresponding to different accident duration “T” 图4为列车追踪时间对事故后果的影响。由图4可以看出,事故持续时间及列车长度确定时,列车追踪时间越长,事故造成的停运列车数量越少,对应的区间停车数量也越少。通过拟合后得出列车追踪时间与停运列车数量关系如图4中虚线所示,表明列车追踪时间越长,对于该条线路运营的影响越小,反之,列车追踪时间越短,突发事故对线路运营的影响越严重。 图4 列车追踪时间t与停运列车数量k关系Fig.4 The relation chart between the headway time “t” and the number of stopped trains “k” 3.2.2 突发事故风险经换乘站传播后对运营影响计算 1)线路2运营延误 由公式(10)计算得线路2每列车在该站的平均运营延误时间为: (12) 2)换2站台客流累积 由公式(11)计算得不同事故持续时间下换2站台客流拥挤度结果如图5所示。 图5 事故持续时间T与换2站台客流拥挤度F(Td)关系Fig.5 The relation chart between the accident duration “T” and the Crowded degree of passengers in platform 2 “F(Td)” 由图5可知,事故持续时间越长,换2站台的客流拥挤度越大。事故持续时间为25 min(1 500 s)时换2站台的客流拥挤度已经达到93.6%,此时由于站台过于拥挤,极易发生拥挤踩踏等事故;同时拥挤度过大,会导致线路2列车在本站产生更大的延误时间,造成线路2更严重的运营延误甚至失效,从而风险将进一步传播至其他线路乃至整个路网。 1)对于事故线路,线路占用率较低时,突发事故造成的停车数量较少且增速缓慢,当线路占用率达到60%左右时,停运列车数量会开始快速增长。 2)线路停运列车数量及区间滞留乘客数量都随着事故持续时间的增长而增多。同时,事故持续时间越长,突发事故造成的停车数量增速越快,事故造成的风险也越大;事故持续时间增大到一定值时,会造成整条线路的运营失效。 3)列车追踪时间越长,事故造成的停运列车数量越少,对应区间停车数量越少,事故风险越小。 4)对于通过换乘站连接的换乘线路,突发事故风险经换乘站传播会造成这些线路的车辆运营延误;同时换乘站由于客流集聚和运营延误的双重效应,导致换乘站失效甚至换乘线路运营失效。2 运营突发事故风险经换乘站传播
2.1 风险分析
2.2 突发事故风险经换乘站传播影响计算
3 实例讨论
3.1 参数确定
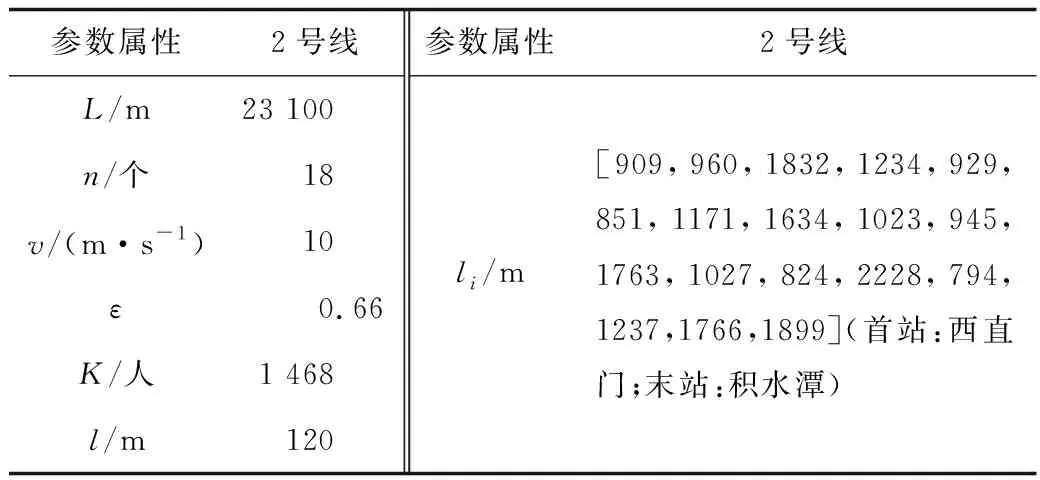

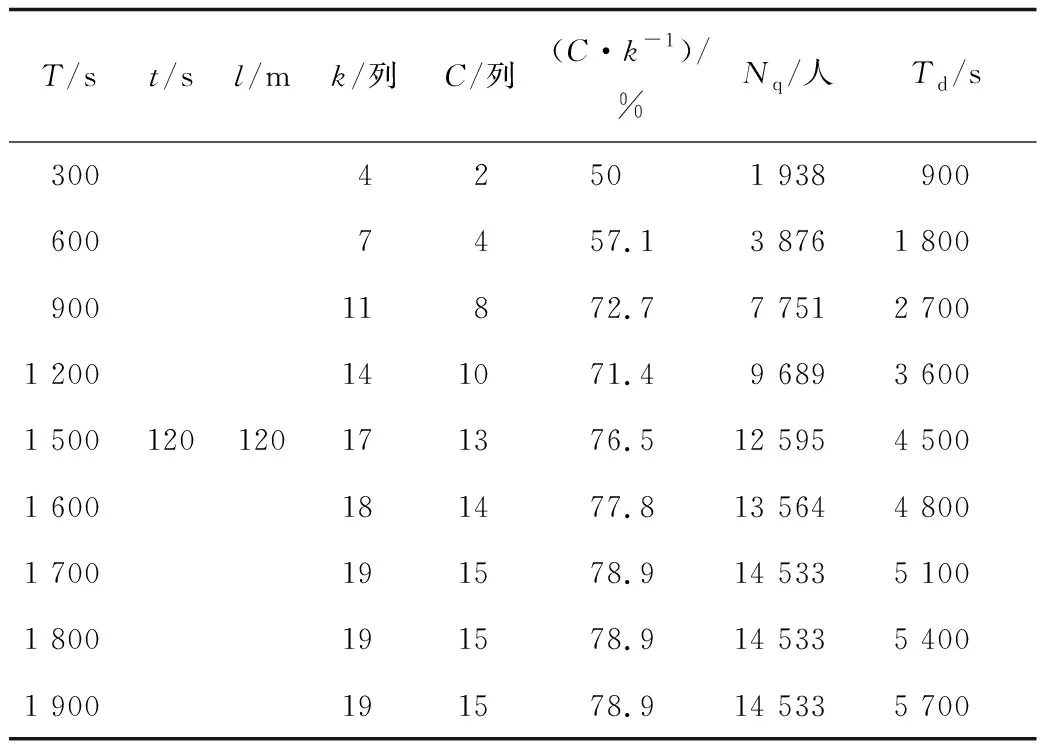
3.2 结果讨论

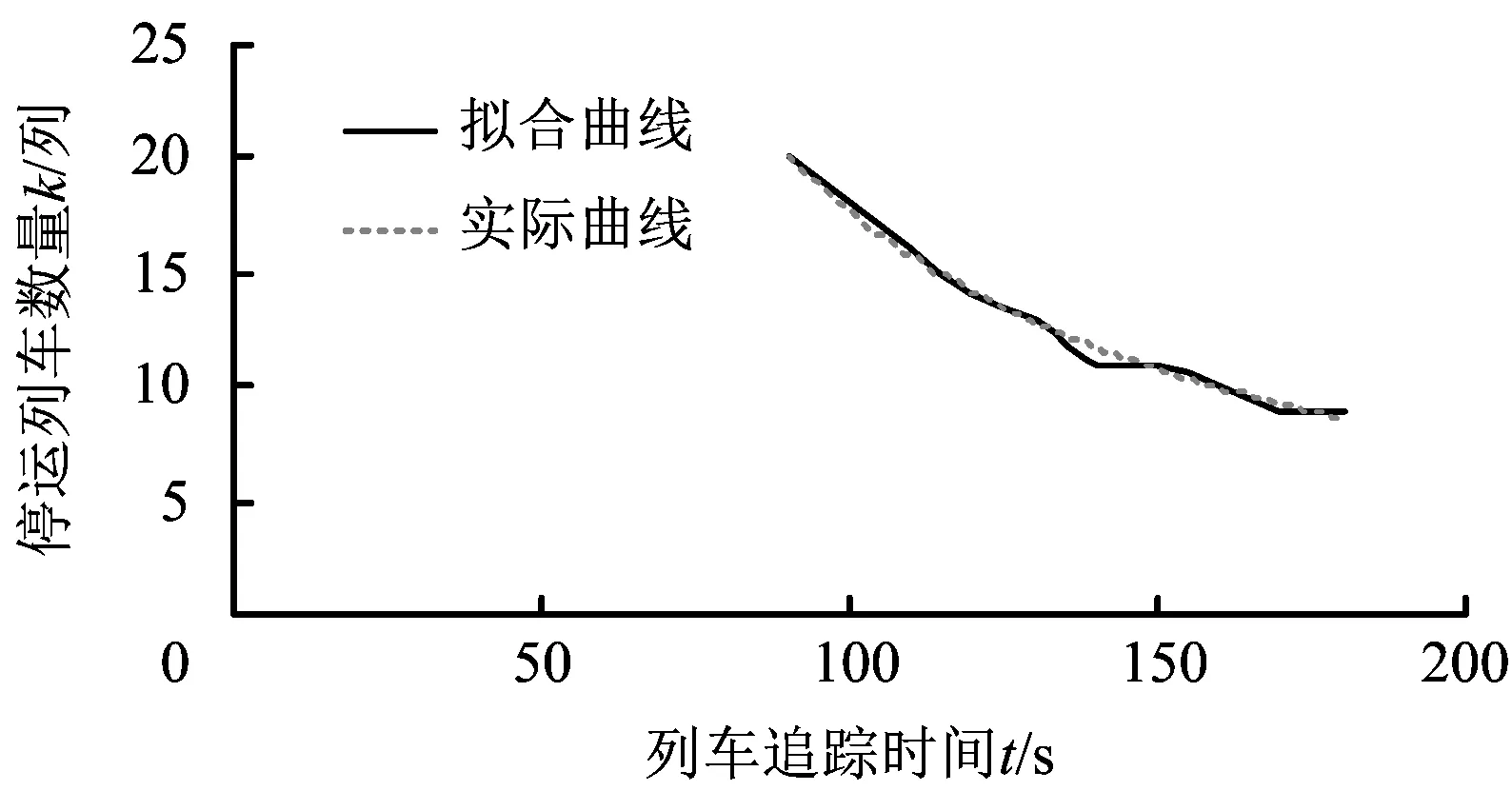

4 结论
