3种典型机器学习方法在灾害敏感性评估中的对比*

张雪蕾,汪 明,曹寅雪,刘 凯,洪超裕

(1.环境演变与自然灾害教育部重点实验室，北京 100875；2.北京师范大学 地理科学学部减灾与应急管理研究院，北京 100875)

0 引言

灾害敏感性是指受灾地区的致灾因子或灾情，对外部环境的敏感程度。灾害敏感性分析和评估是指通过分析孕灾环境敏感性的影响因素建立评价指标体系，利用历史数据评估某一地区的灾害敏感性。因此，灾害敏感性方面的研究往往涉及大样本或高维度数据的处理，因此越来越多的机器学习方法逐渐应用到灾害敏感性分析和评估中。例如，通过贝叶斯网络方法研究北川地区地震滑坡敏感性[1]；结合蒙特卡洛仿真和贝叶斯logistic回归，建立道路建设对滑坡敏感性影响的模型[2]；此外，也有部分学者，采用人工神经网络、支持向量机等对灾害敏感性进行分析研究[3-7]。

在典型机器学习方法中，K近邻认为相似(距离相近)的样本类别相同，其相关概念简洁清晰、易于实现，对于特征性质相似的数据有较好结果，但由于要计算测试样本和所有训练样本的距离，分类速度相对较慢，且特征空间条件不均匀时，误差较大；朴素贝叶斯是通过比较测试样本各类别的条件概率进行预测，由于条件独立性假设，故无需考虑各属性间的关联，且需要估计的参数较少，但在方法的实际应用过程中，相关问题往往很难满足条件独立性假设；决策树是利用特征与类别之间的映射关系进行预测，结构简单，适用于训练集数据量较大的情况，分类速度快，对缺失值不敏感，可以不进行预处理，但决策树不能保证最终的结果最优，且当训练样本含有噪声或类别太多时，性能会受到很大影响；支持向量机是将样本空间映射到一个高维空间，通过划分超平面以对测试样本进行预测，解决了线性不可分的情况，但当训练集规模很大时，算法复杂度增加，进而导致效率不高，并且依靠经验选择核函数会对结果产生影响；神经网络是模拟生物神经系统，通过确定节点及节点之间关系以进行预测，具有较强的迁移性，可以自主地从数据中提取知识，适合于大数据分析，并行分布处理能力强，充分逼近复杂的非线性关系，具备联想记忆的功能，但神经网络需要大量的参数，不能观察学习过程，输出结果难以解释，并且许多实际问题往往不能提供足够的数据，最终导致预测结果产生误差；随机森林构建了多棵决策树，通过投票进行预测，优化了传统决策树容易出现的过拟合问题，并且当处理高维度数据时，不用提前做特征选择，但在对于不均衡样本，随机森林仍有缺陷，并且树的规模过大会使得构建时间过长[8-23]。

综上，不同监督学习方法在敏感性研究中的适用性，特别是针对不同特征样本、不同灾害问题时，如何择优选用、提高分析的可靠性和评估精度，值得进一步深入研究。本文选取K近邻、朴素贝叶斯、随机森林3种典型的监督学习方法，以深圳市城市快递员电动自行车交通事故数据为基础，对研究区域的电动车出险敏感性进行对比研究，探讨方法间的差异、适用条件以及对区域敏感性制图结果的影响，为灾害敏感性研究过程中相关机器学习方法的选择提供参考。

1 数据及模型

1.1 数据及处理

研究区域(深圳市)包括了平原、台地、山峰等多种地貌类型，东部地区林地丰富，西部地区人口较为密集，市内交通状况复杂，电动自行车出行风险暴露高。截至2015年7月，深圳市人均电动自行车占有量约每10人3.52辆[24]，2015年涉及电动车的交通事故共造成114人死亡，占总死亡人数的26.45%，50%左右的伤亡事故与电动自行车有关[25]。

本文所采用的电动自行车出险数据来自于2014年11月至2016年12月深圳市快递员电动自行车交通事故数据集，包含了出险时间、地点、事故简介、损失金额、碰撞类型等；此外，还使用了中国科学院资源环境科学数据中心的以下数据：2010 年全国GDP空间分布公里网格数据、中国100万地貌类型空间分布数据、2010年中国土地利用现状遥感监测数据、2010年全国人口空间分布公里网格数据、中国海拔高度DEM(SRTM 30 m)空间分布数据30米栅格数据、中国地面气候资料日值数据集(V3.0)、中国气象背景——年平均气温(经DEM校正)数据。而道路数据，则使用了Open Street Map世界地图的2016 Open Street Map data矢量数据。

本文利用ArcGIS软件，通过高程数据生成坡度和坡向，并对研究区高程、气温、降水、坡度等数据进行重采样，将其空间分辨率统一到1 km网格。利用道路数据，计算每平方公里网格内的道路总长度，获得深圳市的道路密度；利用数字地图确定出险地点的经纬度信息，获得深圳市每平方公里网格电动车出险次数，根据是否出险将各网格的类别确定为出险、未出险2种情况。经过上述处理，每平方公里网格为1个样本，样本属性包括： GDP、地貌类型、土地利用类型、人口、高程、降水、气温、道路密度、坡度、坡向，总计共生成1 771个样本，其中219个出险样本，1 552个未出险样本。

1.2 模型及流程

1.2.1 K近邻

K近邻将测试样本与训练样本一一比较，提取训练样本集中与测试样本最相似的K个训练样本，根据训练样本的分类情况，对测试样本进行预测。K近邻的流程如图 1所示。

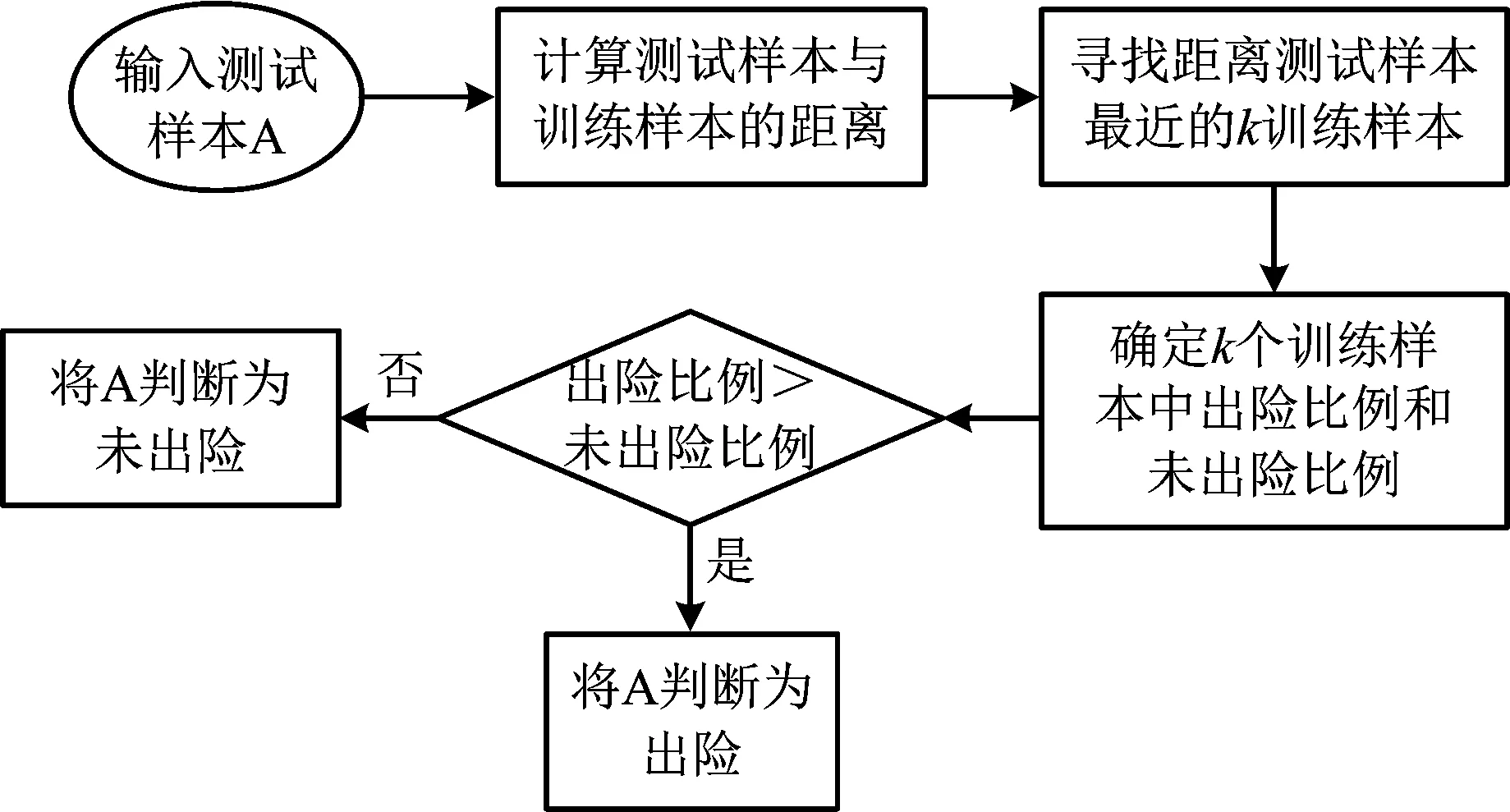
图1 K近邻方法计算流程Fig.1 The flow chart of the K-nearest-neighbor

1.2.2 朴素贝叶斯

朴素贝叶斯计算出险或未出险的条件概率，当测试样本被判断为出险的条件概率大于未出险时，将测试样本判断为出险，反之判断为未出险。图 2所示内容为朴素贝叶斯方法的计算流程。

图2 朴素贝叶斯方法计算流程Fig.2 The flow chart of the Naïve Bayes

1.2.3 随机森林

随机森林可以分为2部分来理解，“随机”和“森林”。“随机”部分是指通过bootstrap对样本进行有放回的随机抽样，进而建立二叉树；“森林”部分是指反复建立二叉树。当测试样本进入森林后，每1棵二叉树都可以得到1个分类结果，再进行“投票”过程，按照投票多寡判定出险与否，具体流程如图3所示。

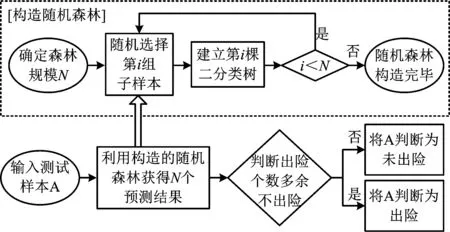
图3 随机森林方法计算流程Fig.3 The flow chart of the Random Forest

2 结果及对比

2.1 准确率与参数分析

深圳市每平方公里网格中未出险样本的比例约达到90%，全部预测为未出险也可以使得准确率达到90%，因此改变样本出险和未出险比例可能会影响模型的预测效果，本文选取了5种样本比例：“全部样本”；“未出险样本”与“出险样本”比例为7∶1；“未出险样本”与“出险样本”比例为5∶1；“未出险样本”与“出险样本”比例为3∶1；“未出险样本”与“出险样本”比例为1∶1。对于3种预测模型，首先确定出险和未出险的样本比例，进而选择三分之一样本作为测试样本，剩余三分之二为训练样本。对于K近邻，不同的K值对分类结果有较大的影响[8]，本文选择K取值2到292(样本比例为1:1时，训练样本的个数是292)；对于朴素贝叶斯，连续变量离散化处理时的分组个数会影响条件概率，进而影响最终的预测结果；对于随机森林，当随机森林规模较小时，分类误差大、性能也比较差[21]，森林的规模可能会影响投票的比例，进而影响最终的预测结果。

评价模型的预测结果时，本文使用准确率和混淆矩阵2种指标。准确率体现了模型总体的预测情况，混淆矩阵可以避免由于过拟合造成的准确率过高[26-28]。

(1)

混淆矩阵中，真阳性(TP)代表出险样本中被预测为出险的百分比；假阴性(FN)代表出险样本中被预测为未出险的百分比；假阳性(FP)代表未出险样本中被预测为出险的百分比；真阴性(TN)代表未出险样本中被预测未出险的百分比。3种预测模型的准确率和混淆矩阵如图4～6所示，图中，左侧子图是不同样本比例和参数下的准确率曲线，右侧子图是不同样本比例下的混淆矩阵。其中混淆矩阵由4个象限构成，每个象限中四分之一圆的半径代表真阳性、假阴性、假阳性、真阴性的取值。

1)从K近邻的准确率可以看到，同一样本比例下，随着K取值逐渐增大，准确率变化不大。其中样本比例为1∶1时，当K取值接近训练样本个数时，准确率迅速下降到样本比例50%；随着样本出险和未出险比例接近于1∶1，准确率逐渐降低。在同一样本比例下，选择使得准确率最高的K值绘制混淆矩阵；随着样本比例接近于1∶1，未出险样本的预测准确率逐渐降低，出险样本的预测准确率逐渐升高，且在样本比例为1∶1时，出险样本和未出险样本的预测准确率非常接近。对于敏感性分析来说，更需要关注出险样本的预测准确率，以便进行风险管控。因此，对于K近邻来说，样本比例为1∶1时预测结果更好。

2)从朴素贝叶斯的准确率可以看到，同一出险和未出险样本比例下，随着连续变量分类个数逐渐增大，准确率变化不大，其中连续变量分为2类时准确率较高。不同出险和未出险样本比例下，准确率的差异不明显。在同一样本比例下，选择准确率最高的连续变量分类个数，绘制混淆矩阵。全部样本，样本比例为7∶1，5∶1，3∶1时，未出险样本准确率远高于出险样本准确率，显然出现了过拟合现象；在样本比例为1∶1时，对出险样本的预测准确率高于未出险样本。

3)从随机森林的准确率可以看到，同一出险和未出险样本比例下，随着森林规模的增大，准确率始终在某一值附近波动；不同出险和未出险样本比例下，随着样本比例接近1∶1，准确率逐渐降低，波动性逐渐增强；在同一样本比例下，选择准确率最高的森林规模，绘制混淆矩阵。对于随机森林来说，随着样本比例接近于1∶1，对于未出险样本的预测准确率迅速降低，出险样本的预测准确率迅速升高，在样本比例为1∶1时，对出险样本的预测准确率较高于未出险样本。

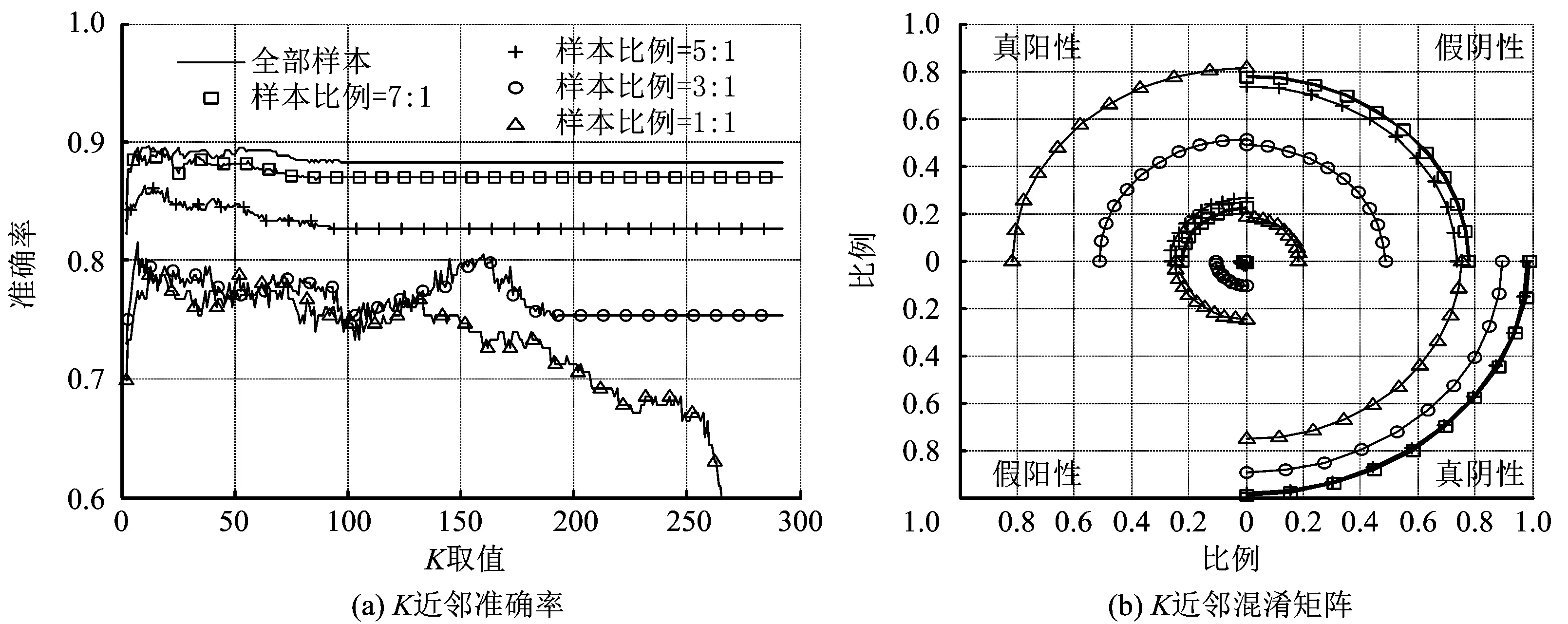
图4 K近邻准确率和混淆矩阵Fig.4 Accuracy rate and confusion matrix of K-Nearest-Neighbor

图5 朴素贝叶斯准确率和混淆矩阵Fig.5 Accuracy rate and confusion matrix of Naïve Bayes

图6 随机森林准确率和混淆矩阵Fig.6 Accuracy rate and confusion matrix of Random Forest

通过3种方法的准确率和混淆矩阵对比可以看出：随机森林、K近邻的准确率对样本比例比较敏感，朴素贝叶斯相对不敏感；朴素贝叶斯的混淆矩阵对样本比例比较敏感，K近邻和随机森林较不敏感；3种方法都在样本比例为1∶1时预测效果最好，此时，K近邻对2类样本预测效果相近，朴素贝叶斯对出险样本预测较好，随机森林介于K近邻、朴素贝叶斯之间。

2.2 敏感性图

使用3种监督学习方法绘制敏感性图，首先需要确定不同方法中表征敏感性的指标。在使用K近邻的结果绘制敏感性图时，可以得到与测试样本最相似的K个训练样本中出险样本的比例，以该比例作为评价该样本的敏感性指标；在使用朴素贝叶斯绘制敏感性图时，将每个测试样本出险的条件概率作为评价该样本的敏感性指标；在使用随机森林绘制敏感性图时，将每个测试样本判定为出险的投票比例作为评价该样本的敏感性指标。对于每种算法选择准确率和混淆矩阵结果均最好的参数对所有样本进行预测，获得敏感性指标，即可获得深圳市电动车出险的敏感性图。3种方法的敏感性图分别为图 7、图 8、图 9。

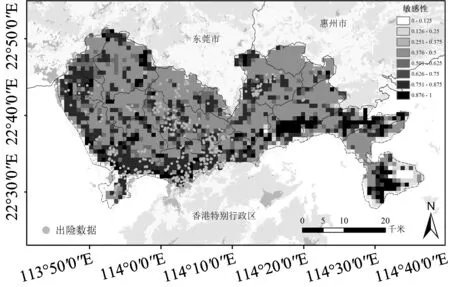
图7 K近邻敏感性图Fig.7 Susceptibility map of K-Nearest-Neighbor

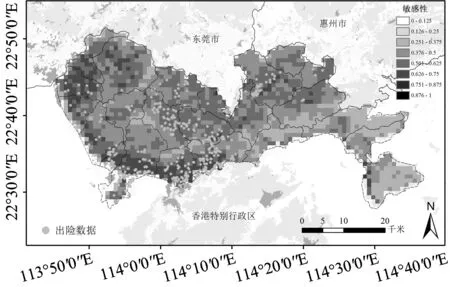
图8 朴素贝叶斯敏感性图Fig.8 Susceptibility map of Naïve Bayes

图9 随机森林敏感性图Fig.9 Susceptibility map of Random Forest

3种方法得到的敏感性图对于道路密集、出险发生较多的地区都评估出了较高的敏感性。但是，K近邻方法对于主要为林地、电动车出险可能性较低的东部地区预测结果较差，出现了高敏感性和低敏感性的突变，另外，在敏感性较低的区域，会出现较高的异常值；朴素贝叶斯和随机森林得到的敏感性图比较相近，交通发达地区的敏感性普遍较高，对于林地地区的敏感性较低，随机森林方法对林地的敏感性几乎判别为0。总体来说，3种方法中，随机森林的结果最符合出险分布，朴素贝叶斯次之，K近邻结果最差。

3 讨论

1) K近邻方法是通过比较样本之间相似性对测试样本进行评估。对于敏感性研究来说，高程、降水等环境相似的地区会形成相似的孕灾环境和敏感性。因此，使用K近邻进行灾害敏感性分析从原理上有意义，保证了对出险和未出险2类样本预测准确率均较高。另外，由于K近邻对于样本比例敏感性较强，对于敏感性分析问题要先进行样本筛选工作。在度量2个样本相似性时，由于部分变量差异较大，会出现将2个样本的敏感性预测为完全不同的结果。以深圳市东部地区为例，该地区主要以林地为主，但是K近邻判别的敏感性却出现了突变，这是由于2地区的坡度、高程、坡向存在显著差异，温度和地貌类型存在部分差异。在利用K近邻进行敏感性分析时，如果特征的单位对欧式距离影响较大，可以通过归一化处理消除该影响。分类变量数值化方法的不同也可能对K近邻的结果带来影响。本文对地貌类型、土地利用类型定义了哑变量，其准确率和混淆矩阵都远差于现有结果。另外，本文也利用内积距离、余弦距离计算样本间距离，准确率和混淆矩阵都差于欧氏距离。

2) 朴素贝叶斯方法考虑到了历史出险样本可能出险的所有情况，对未来灾害进行概率评估。由于朴素贝叶斯的准确率对于样本比例不敏感，在不能对于样本的分布进行判断时，朴素贝叶斯的准确率具有参考价值。朴素贝叶斯对于出险样本的预测结果要好于未出险样本，更关注于可能的高敏感性样本，更适合风险分析。但是计算条件概率时要注意避免概率为0的情况，可在计算过程中，对概率加常数、取对数，因此出险和未出险的条件概率可能得到大于1的伪概率值。此时，可以将出险和未出险的伪概率求和，求得出险伪概率所占比例作为敏感性指标。在利用朴素贝叶斯进行敏感性分析时，也要注意分类变量的类别划分。本文对照了土地利用类型、地貌类型多种分类方式的预测准确率和混淆矩阵，结果显示差别不大。

3)由于通常认为集成学习器可获得比单一学习器显著优越的泛化性能，因此在敏感性研究中，将集成学习方法与单一学习方法对比具有一定意义。对于深圳市电动车出险敏感性来说，土地利用类型是否为建设用地可能直接影响结果，因此，使用特殊的二叉决策树——随机森林，在原理上存在一定意义。随机森林的整体准确率、出险样本的预测准确率对样本比例比较敏感，因此，在使用随机森林进行敏感性分析时，要先进行样本筛选工作。在利用随机森林进行敏感性分析时，构建二叉树的方法包括Accuracy、Gini、MDL等。通过对比发现，不同的方法对准确率和混淆矩阵的结果影响不大。由于使用了投票比例作为敏感性指标，其取值范围为[0,1]，无需进行任何处理即可绘制敏感性图。

4 结论

1)运用K近邻、朴素贝叶斯、随机森林3种监督学习方法，通过设置不同参数和样本比例训练模型，通过准确率曲线和混淆矩阵比较了3种方法在灾害敏感性评估中的效果，分析了3种方法的差异和适用条件。

2)由于K近邻算法是利用距离度量样本之间相似性，因此，当样本数据的某一变量差异性较大时，或者不同变量的单位存在很大差异时，应尽量避免直接使用K近邻算法。但是，当灾害敏感性与地理相对位置相关性较强时，选择K近邻算法更有理论意义。

3)在利用机器学习方法对灾害敏感性进行评估时，变量的选择会影响敏感性评估结果。由于朴素贝斯算法的准确率对样本比例不敏感，因此可以使用它避免反复随机抽样对计算效率带来的负面影响。

4)当样本数量大于1 500时，K近邻算法、朴素贝叶斯算法、随机森林算法的评估结果非常接近，但是随机森林的效率明显低于其他2种方法，因此在样本数量较大时，单独使用K近邻和朴素贝叶斯算法即可得到较好的评估结果。另外，在随机森林的评估结果中，低敏感性区域和高敏感性区域差异较大，低敏感性区域的敏感性几乎为0。但是，对于大多数灾害来说，没有发生过灾害的区域不代表不会发生灾害，因此随机森林在敏感性分析时也需要关注过拟合的问题。