基于Isight的径向磁悬浮轴承结构优化设计
2018-08-04周瑾高天宇董继勇陈怡高素美
周瑾,高天宇,董继勇,陈怡,高素美
(1.南京航空航天大学 机电学院,南京 210016;2.南京磁谷科技有限公司,南京 211102;3.金陵科技学院,南京 211169)
主动式磁悬浮轴承(Active Magnetic Bearing)具有无接触、无磨损、无需润滑等优点,广泛应用于涡轮机、医疗设备、机床或有真空和严格卫生要求的工作环境中[1]。电磁轴承的支承性能受其机械结构、控制电路等多方面影响,其中,磁极尺寸、气隙大小、线圈匝数等,机械结构参数对其磁感应强度分布和电磁力有直接影响,合理的结构参数设计能够最大程度地利用励磁线圈提供的励磁磁势,从而提高磁轴承的承载能力并减少运行损耗[2],因此,近年来国内外众多学者针对主动磁悬浮轴承的机械结构优化设计进行了研究。文献[3]提出了电磁轴承系统设计的一些基本规范,并使用有限元软件对磁轴承的电磁性能进行了分析;文献[4]通过测量磁感应强度随温度的变化,推导出了导线直径、匝数、磁极宽度等参数的约束方程,并以此为基础对磁轴承进行了结构优化;文献[5]设计了一套磁轴承结构参数化建模软件,成功应用于磁轴承的结构设计和工业制造过程;文献[6]提出了使用Isight集成ANSYS优化磁轴承结构的方法。以上研究对象多为4极、8极径向磁悬浮轴承,此类轴承极间齿槽相对于所容纳的2匝绕组空间宽裕,因此优化过程中大多忽略绕组截面对齿槽形状的影响。文献[7]在对8极均布径向磁悬浮轴承磁极与齿槽形状综合优化过程中,将绕组截面设为矩形并给出了矩形各边长相对于齿槽的约束条件,但对齿槽形状做了较多简化,并不能很好地反映绕组的具体位置情况。
为了适应大直径、大吨位的承载要求,对某大型卧螺离心机用径向磁悬浮轴承进行优化,设计使用16极均布径结构,在磁极与齿槽形状的综合优化设计过程中,为了避免相邻绕组线圈骨架装配干涉的情况,需准确计算绕组匝数、骨架所占空间并判断骨架的实际装配位置,以保证优化结果的可行性。通过UG建模软件构造磁轴承参数化装配模型和装配可行性的判断依据,并在ANSYS软件中分析磁轴承的电磁性能[8];使用Isight集成优化平台集成MATLAB,UG,ANSYS等软件[9],通过改变磁轴承内部结构尺寸探索其最大承载力。
1 磁悬浮轴承建模
卧螺离心机用径向磁悬浮轴承(图1)采用16极结构,设计径向载荷为20 520 N,其主要结构参数见表1[10]。

图1 卧螺离心机用径向磁悬浮轴承Fig.1 Radialmagnetic bearing for horizontal screw decanter centrifuge

表1 径向磁悬浮轴承结构参数Tab.1 Structural parameters of radialmagnetic bearing
装配线圈骨架的磁悬浮轴承二维模型如图2所示,图中:h为骨架每侧厚度;h1为绕线区壁厚;l为骨架高度;l1和l2分别为上、下骨架边缘厚度。
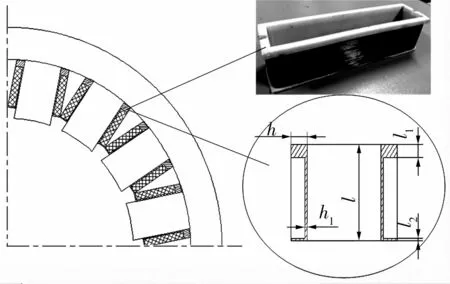
图2 径向磁轴承与绕线骨架装配示意图Fig.2 Assembly diagram of radial magnetic bearing and winding frame
通过以上骨架几何参数和表1中漆包线直径,取骨架凹槽内励磁绕组占空比为0.68,可以得到骨架结构与其所能承载的线圈匝数之间的关系为
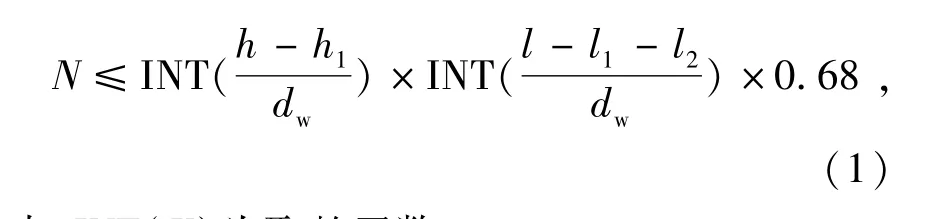
式中:INT(X)为取整函数。
在设计过程中,一般将线圈骨架的横截面设为矩形,由于定子槽底圆角的存在,骨架在定子槽中的实际装配位置会出现图3所示的2种情况:当槽底圆角较小时,骨架顶角与槽底接触而另一顶角与圆角间留有间隙(位置a);当槽底圆角较大时,骨架顶角与圆角接触而另一顶角与槽底间留有间隙(位置b)。因此,当几何建模考虑绕线骨架的存在时,必须对以上2种情况分别建模,才能准确表达骨架位置并判断相邻骨架是否出现几何交叉。

图3 线圈骨架的2种装配情况Fig.3 Two assembly types of winding frame
建模时为了能够准确识别装配位置形式,根据线圈骨架与槽底的几何关系,推导出骨架2顶点同时与槽底和圆角接触的临界圆角半径作为判断骨架装配位置形式的标准。
骨架装配的临界位置如图4所示,图中:A,D为槽底圆角边界点;B为圆角圆心;GF为骨架顶边,与定子槽侧壁OD垂直。设骨架内壁与定子槽壁装配间距EF=CD=s;圆角半径AB=BF=BD=r;△OGE中,∠GOE =82°,由此可得上述参数的数学关系如(2)式所示,即可由设计的线圈骨架结构参数得到临界位置的圆角半径r,
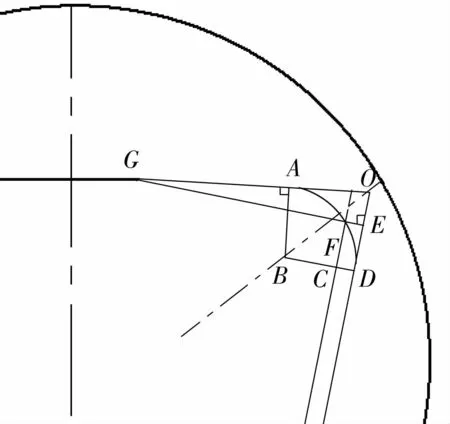
图4 线圈骨架临界装配位置Fig.4 Critical assembly position ofwinding frame
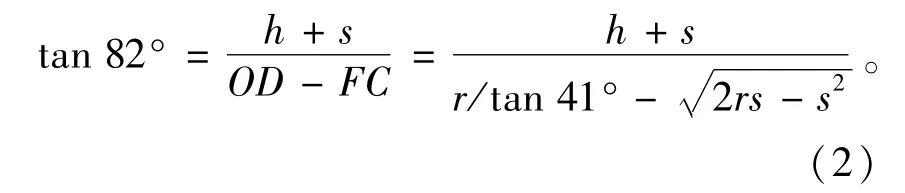
根据临界圆角判断骨架实际装配位置,在三维建模软件UG中建立磁悬浮轴承参数化模型,如图5所示。由于磁悬浮轴承磁路部分的结构沿轴向形状、尺寸相同,因此只需计算一组磁极(1/4定子)在设定电流下的承载力。在模型中测量右上骨架左下角点与原点连线和水平线夹角θ,当θ>90°时,表明两骨架在装配时会出现干涉而无法装配,结构参数设计无效。
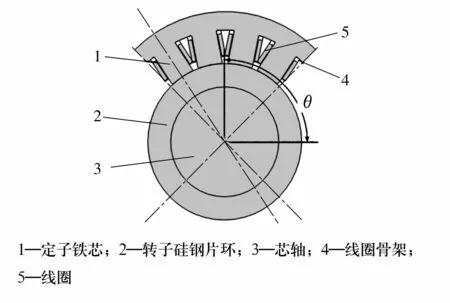
图5 磁悬浮轴承系统机械结构建模Fig.5 Modeling ofmechanical structure formagnetic bearing system
2 磁悬浮轴承电磁性能分析
2.1 电磁力理论分析
主动磁悬浮轴承对转子的支承性能与其电磁参数密切相关,对磁轴承平面模型的y方向受力情况进行分析,如图6所示。图中:α1,α2为磁极中线与y轴的夹角;δ为气隙。

图6 转子在单自由度上的受力Fig.6 Load of rotor on single degree of free dom
假设单个磁极面积为S0,空气磁导率为μ0,气隙之间没有漏磁,且磁感应强度相同,则一组磁极对转子的合力为
式中:fy1为单个磁极对转子的电磁吸力。

由于磁轴承定子的工作磁密一般设计在硅钢材料磁化曲线的膝部,励磁磁势与磁感应强度已不是严格的线性关系,尤其在励磁电流较大、硅钢片趋近饱和时,由(3)式所得的电磁力往往与实际产生较大误差,因此需用有限元法对电磁力做进一步的精确分析。
2.2 电磁力有限元计算
采用ANSYS对径向磁悬浮轴承进行电磁场仿真,导入磁悬浮轴承平面模型,将磁轴承几何模型分为定子铁芯、转子硅钢环、线圈、芯轴和空气材料区。对硅钢材料的定子铁芯和转子硅钢环赋图7所示的B-H磁化曲线。使用四边形网格单元划分模型,对小间隙处如定转子气隙等部分进行网格加密以保证计算精度。有限元网格划分如图8所示。
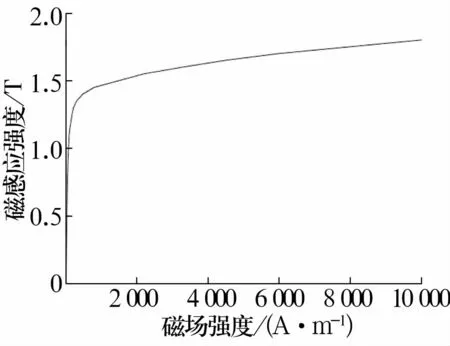
图7 硅钢片的B-H曲线Fig.7 B-H curve of silicon steel sheet
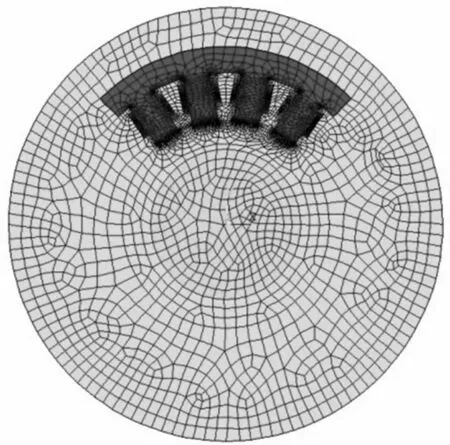
图8 网格划分Fig.8 Meshing
由于径向磁悬浮轴承采用差动控制,当上部磁极电流为2倍的偏置电流(6 A)、下部磁极电流为0时可得其最大承载力。设计磁轴承绕组匝数为100匝,赋每极安匝数NI=600 A,有限元计算得到单组磁极可提供82 859 N/m的竖直方向电磁力,对于实际轴向长度180mm、定子的4组磁极以45°斜置安装的磁悬浮轴承,其竖直方向最大承载力为21 092 N,满足径向最大电磁力设计要求。
ANSYS仿真得到的磁力线分布和磁感应强度分布分别如图9和图10所示。由图可知,定子齿和定子轭部磁密均达到1.6 T,接近硅钢片材料饱和点1.7 T,槽底边角处磁密1.8 T,已达到局部饱和。对于磁悬浮轴承,定子材料的饱和降低了励磁磁势的利用率,同时增大了定子的损耗和发热,故设计时需在定子结构中尽量避免尖锐边角,以防止局部饱和对磁轴承性能的影响。
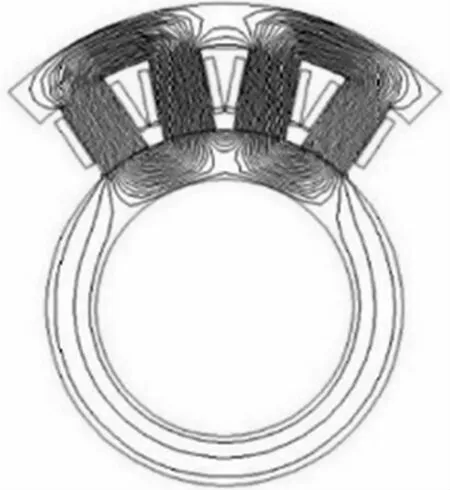
图9 磁力线分布Fig.9 Distribution ofmagnetic force line
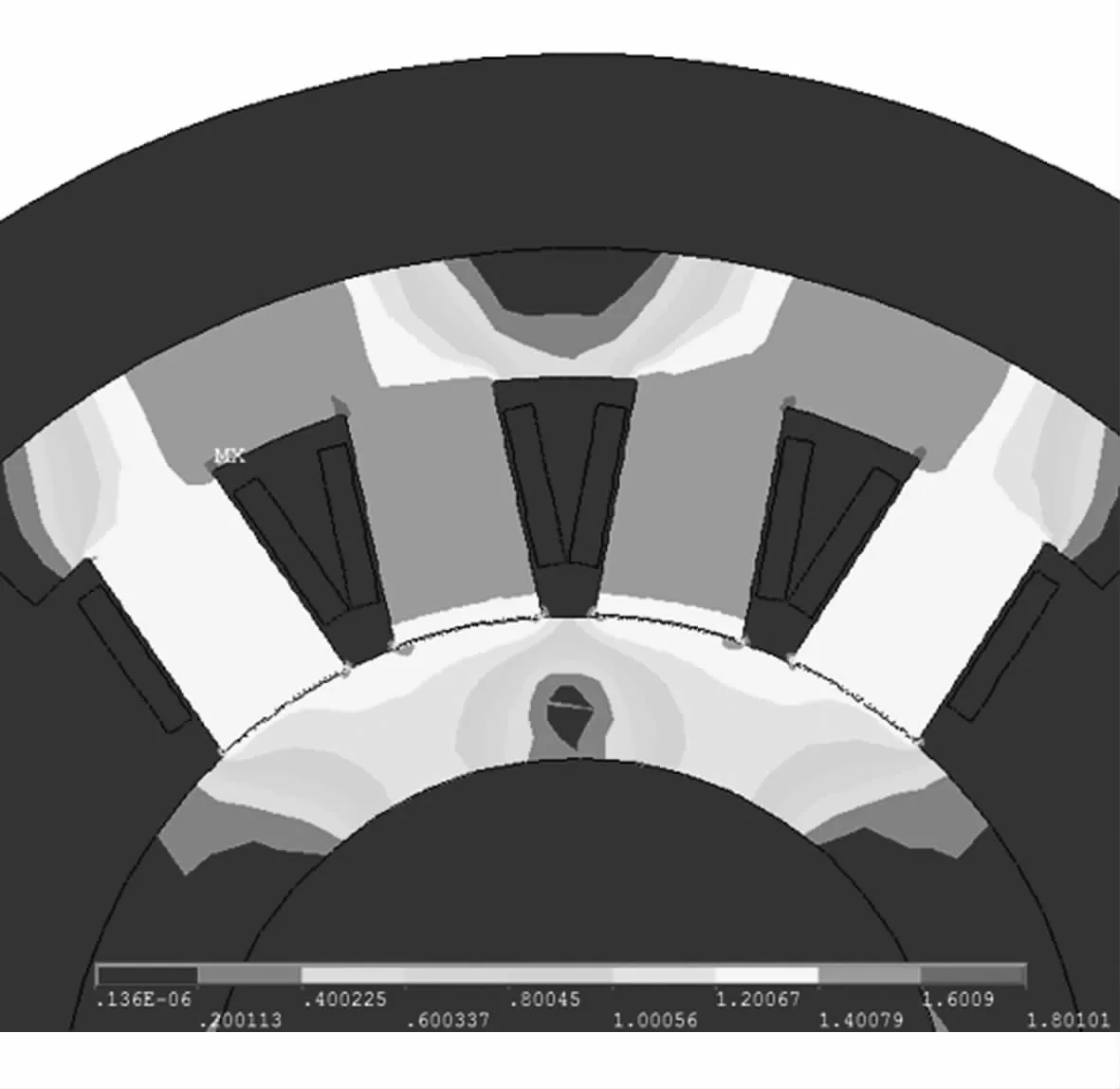
图10 磁感应强度分布Fig.10 Distribution ofmagnetic induction intensity
3 基于Isight的集成优化分析
3.1 Isight 集成过程
通过Isight软件搭建集成MATLAB,UG,ANSYS等软件的优化平台,如图11所示。
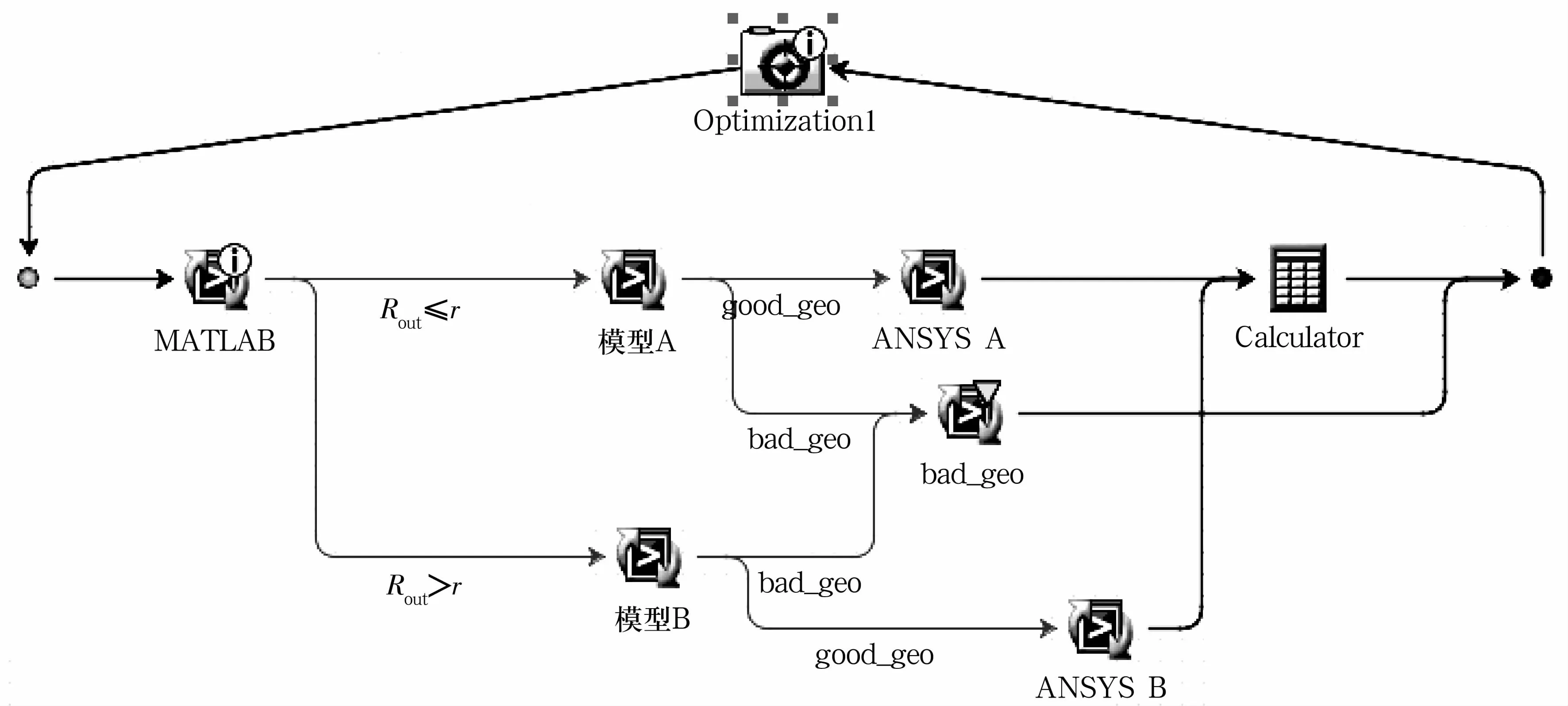
图11 Isight优化平台建立Fig.11 Establishment of the Isight Optimization Platform
具体步骤如下:
1)集成MATLAB:调用MATLAB组件读取磁轴承结构几何参数,计算电流密度J、绕线匝数N和临界倒角r;
2)设定sm-flow运行条件:判断设计变量Rout与所求临界倒角r的关系,若Rout≤r,则进入位置a预设模型A;若Rout>r,则进入位置b预设模型B;
3)集成UG:导入各参数变量,按照相应位置生成2D模型并测量θ;
4)设定sm-flow运行条件:以θ值判断几何模型有效性,若θ≥90°,则参数无效,进入MALAB组件bad_geo,将电磁力计算结果赋值为0,作为无效参数的标志;若θ<90°,则参数有效,进入相应的ANSYS有限元分析组件;
5)集成ANSYS:将各材料电磁参数加载到导入的对应模型中进行电磁力计算,得到单组磁极即1/4定子单位长度电磁力Fmagnetic;
6)集成Calculator计算器组件,将有限元分析得到的单位长度电磁力Fmagnetic乘以磁轴承轴向长度,得到单组磁极最大电磁力Fmagall。
3.2 磁轴承几何参数对电磁力的影响
由磁轴承几何建模可知,除了内外径和齿槽宽度等基本参数以外,其槽底和齿顶圆角对整体装配和电磁性能也有一定的影响,因为以上几何尺寸不便在数学模型或ANSYS平面模型中直接修改,因此对这部分结构的优化设计研究较少。现利用搭建完成的Isight集成平台对磁悬浮轴承各关键几何尺寸对电磁力的影响进行分析。
磁轴承结构设计变量如图12所示,在Isight中使用设计试验组件DOE,采用控制变量和全因子设计方法分析几何尺寸对电磁力的影响,选择转子硅钢环外径D2、定子槽底直径D4、槽底圆角半径Rin、齿顶圆角半径Rout和半磁极宽度Whalf为自变量,全因子设计对各变量在变化范围内等分20个点并依次进行分析,分析结果如图13所示。
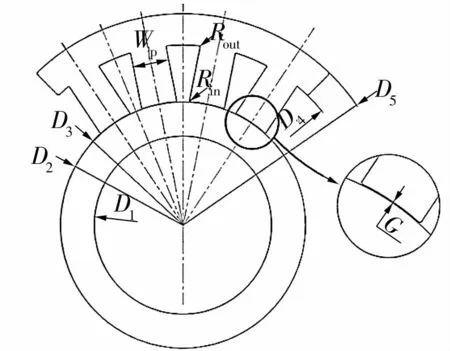
图12 设计变量示意图Fig.12 Diagram of design variables
由图13可知,转子硅钢环外径、半磁极宽度的增大以及槽底圆角半径、定子槽底直径的减小,都会增加定子磁力线流通面积,降低定子内磁饱和程度,提高励磁磁势利用率,进而提高磁悬浮轴承电磁力;齿顶圆角半径增大,相当于增加了定转子间气隙,降低了气隙磁密,使电磁力下降,但为了降低局部磁密,一般仍对齿顶边做圆弧处理。此外,定子内径和半磁极宽度参数扫描过程中出现了电磁力为0的情况,说明在该定子参数下原励磁绕组骨架的装配会发生干涉,需要重新设计。
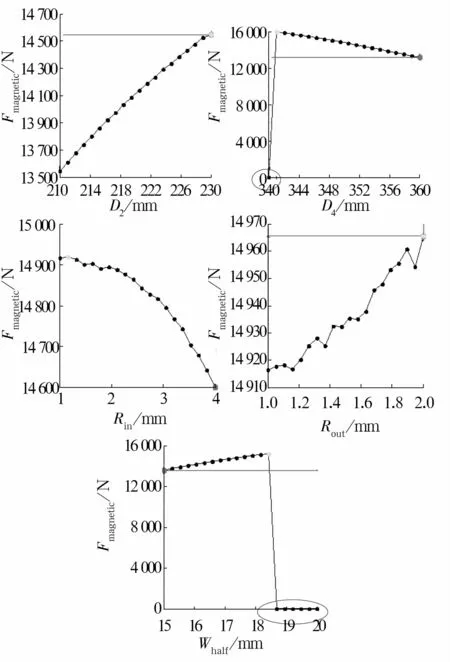
图13 磁轴承几何结构对电磁力的影响Fig.13 Influence of geometry ofmagnetic bearing on electromagnetic force
3.3 磁悬浮轴承几何参数优化设计
将试验设计组件DOE替换为优化设计组件Optimization,选择MIGA全局优化算法对磁轴承各结构参数进行优化。为保证磁轴承与原卧螺离心机的机座装配性能,保持其定子外径、芯轴直径和轴向长度的设计值不变,优化变量设置见表2。以N≥100为约束条件,求取单组磁极在绕组电流6 A下所能获得的最大电磁力Fmagall。Isight优化流程如图14所示。

图14 Isight优化流程Fig.14 Optimal process of Isight
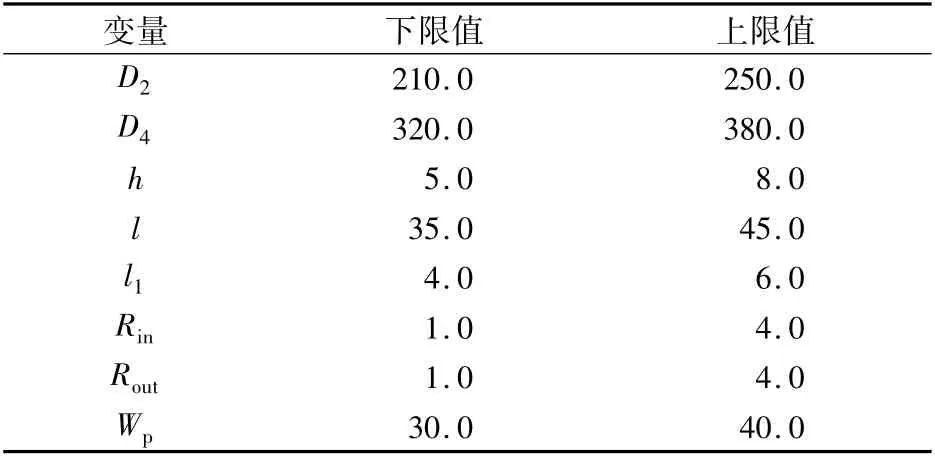
表2 磁轴承结构变量设置Tab.2 Setting for structure variables ofmagnetic bearing mm
Isight优化结果见表3。由表可知,最大电磁力从14 914.62 N提高到16 686 N,提高11.88%。优化后磁轴承在最大承载工况下的磁密分布云图如图15所示。由图可知,由于磁极、磁轭宽度等结构尺寸的适当增加,保证了定子齿、轭磁密在气隙磁密增大10%下最大磁密不超过1.54 T,没有达到饱和,在励磁绕组安匝数保持不变的情况下,极大地提高了励磁磁势的利用效率。

图15 优化后磁密分布Fig.15 Distribution of optimized magnetic flux density

表3 磁轴承结构优化结果Tab.3 Optimal results ofmagnetic bearing structure
设定磁轴承单组磁极承载力14 914.62 N,即优化前磁轴承每组磁极承载力极值,计算得到所需安匝数NI=549.7 A,由于优化前后每极绕组匝数相同(100匝),因此,在相同承载力下,优化后的磁轴承所需电流和能耗较优化前下降了8.38%,由电流造成的绕组铜耗降低了15.9%,优化效果良好。
4 结束语
建立了16极均布径向磁悬浮轴承装配模型,讨论了线圈骨架在磁轴承中的2种装配位置,并以骨架的实际装配情况建立了磁轴承结构参数是否合理的判断依据;通过ANSYS对完成建模的磁轴承进行电磁场分析,得到了电磁分布结果并检验了磁轴承的承载能力;通过Isight分别集成MATLAB,UG,ANSYS等软件,建立了输入模型参数与输出电磁力的计算流程,得到了磁轴承各结构参数对电磁力的影响关系,通过Isight优化设计组件,获得了一组工程可行的优化结果,结果表明:磁轴承承载力和励磁磁势利用率提升了11.88%,在同等工况下磁轴承能耗和损耗大大降低,优化效果良好。建立的磁轴承结构优化流程提高了设计效率,为磁悬浮轴承的结构优化设计提供了一套有效的借鉴方法。
