地震工况下开放型90°推力球轴承的爬坡角

孔宪超，罗继伟

（1.一重集团大连设计研究院，辽宁 大连 116600；2.洛阳轴承研究所有限公司，河南 洛阳 471039）

1 概述

开放型90°推力球轴承广泛应用于大型低速回转设备的方位轴系中，例如：用于大型核电装备的旋转屏蔽塞轴系，通过旋转实现控制棒驱动机构精确定位，保证换料功能［1－2］。该类轴承是设备主要的承载和运动部件，安装在动平台顶板下部，某动平台轴承安装位置如图1所示。由于放开了沿轴线方向的自由度，该类轴系只能利用设备自身重量约束其沿轴线方向的移动，旋转轴线为铅垂方向［2］。

图1 某动平台轴承安装位置示意图Fig.1 Diagram of installation position of a moving platform bearing

鉴于该类大型机动平台的设计寿命动辄要求几十年，期间必须考虑地震以及其他各项振动对轴承性能的影响。地震载荷以动载荷的形式作用于转动平台，可采用等效静力法将动载荷转化为1个轴向方向和2个径向方向的地震载荷。动平台轴承一般采用90°推力球轴承，主要承受推力载荷，可抵抗瞬时轴向方向的地震载荷。为抵御径向方向的地震载荷，轴承采用开放型结构，其特点是允许轴圈在径向和轴向移动一定距离。在径向和轴向方向地震载荷的共同作用下钢球将产生爬坡现象并推动轴圈移动以吸收地震能量。在设计上要求钢球的爬坡幅度不能超出轴承挡边高度，否则会造成事故。鉴于此，提出了安全爬坡角的概念，并提出若不满足安全爬坡角时可在径向设置限位装置。

2 轴承爬坡角

开放型90°推力球轴承的“开放型”是指轴承轴圈不受限，允许在轴向和径向移动。在径向载荷作用下轴承钢球会出现爬坡现象，不同位置处钢球的爬坡角β不同，最大爬坡角βmax如图2所示，Δa，Δr分别为轴承轴圈产生的轴向和径向位移，由几何关系可得

图2 爬坡角示意图Fig.2 Diagram of climbing angle

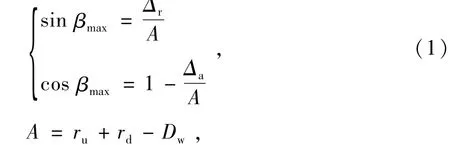
式中：A为轴圈、座圈沟道曲率中心的距离；ru，rd分别为轴圈、座圈沟道的曲率半径；Dw为钢球直径。

对于开放型推力球轴承，轴承产生径向、轴向位移时接触角会发生变化，钢球爬坡角也会发生变化，其爬坡角大小与钢球所处位置有关。不同位置处钢球爬坡角与径向位移的关系如图3所示，不同位置角处的爬坡角可表示为

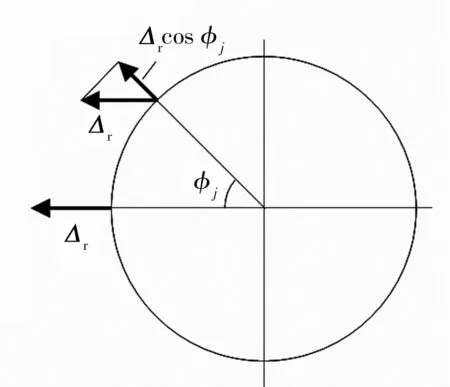
图3 径向位移和爬坡角的关系Fig.3 Relationship between radial displacements and climbing angles

式中：φj为第j个钢球相对于最大爬坡角位置钢球的方位角，最大爬坡角位置对应的为方位角为0的位置；βj为第j个钢球的爬坡角。

3 轴承受载分析

由于该开放型轴承的轴圈不受限，在没有外力作用下，轴承轴圈相对于座圈可任意移动，即初始游隙可变。当该轴承在某径向外载荷Fr作用下达到平衡时，位移Δr或Δa可以理解为该轴承的初始游隙。由于钢球与轴圈、座圈总的法向接触弹性变形量很小，因弹性变形引起的爬坡角的变化量也很小。可近似采用图3几何关系得到任意方位角φj处钢球与轴圈、座圈接触总的法向弹性变形为

式中：kn为轴承接触刚度，可参考文献［6］132得到。

在径向载荷Fr作用下，钢球的接触载荷分布如图4所示。

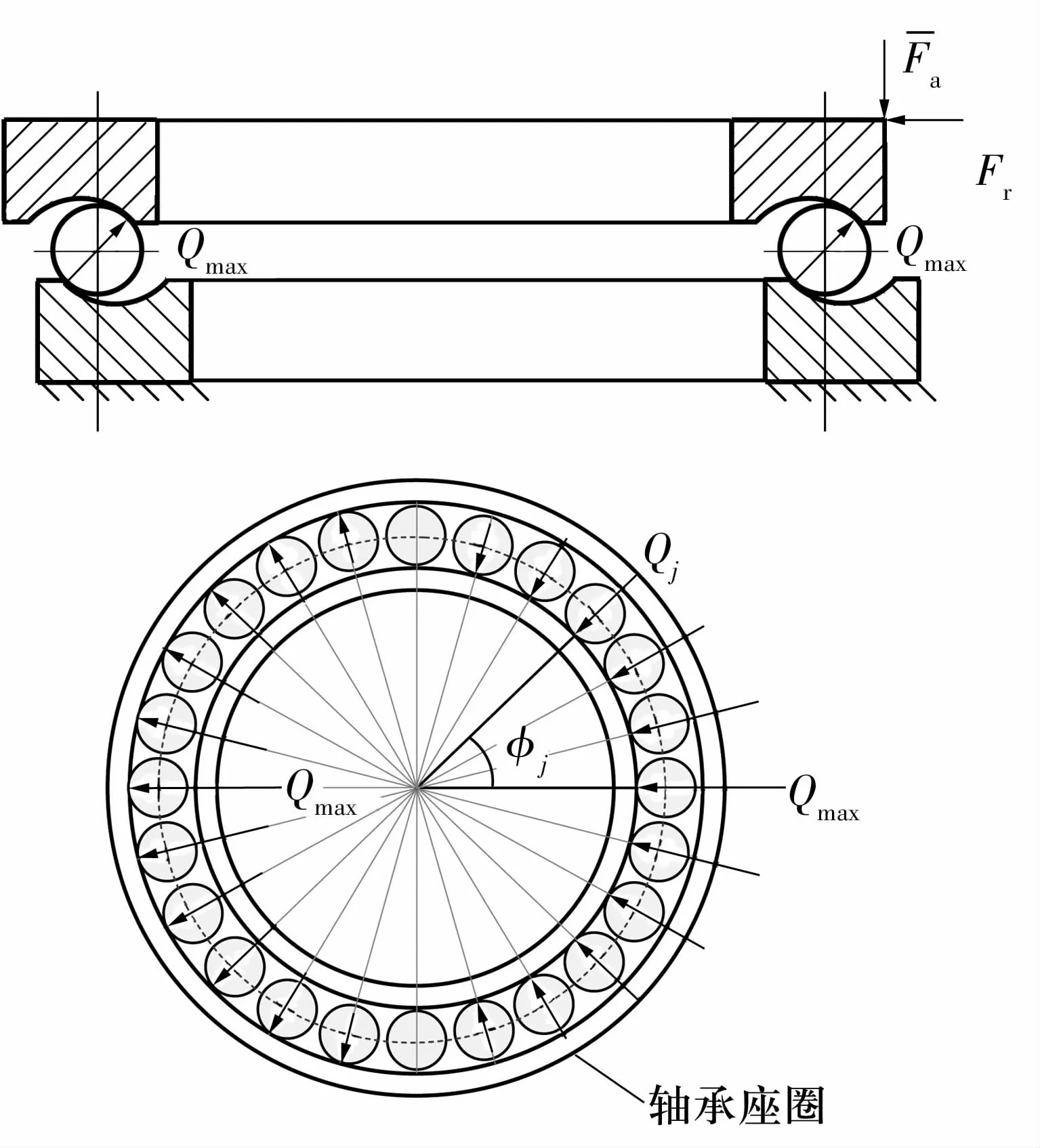
图4 钢球接触载荷分布图Fig.4 Diagram of contact load distribution of steel balls

4 安全爬坡角的条件及径向限位

4.1 安全爬坡角的条件

如图5所示，在极限径向载荷作用下开放型90°推力球轴承钢球与沟道接触椭圆的长半轴刚好达到轴承挡边边缘，钢球爬坡达到极限位置。由于90°推力球轴承轴、座圈完全对称，只需考虑下挡边的这种状态。

图5 极限径向载荷下球与滚道接触示意图Fig.5 Diagram of contactbetween ball－raceway under limiting radial load

当轴承在几何极限爬坡角位置平衡时，即（22）式等号成立的情况下，轴承轴圈的径向、轴向方向的极限位移分别为

式中：βcr为轴承在几何极限爬坡角位置平衡时的βmax。

4.2 限位装置

当该爬坡角不满足（22）式时，实际爬坡角将超过安全爬坡角，即βmax＞β0－αa，钢球会脱出沟道。可通过设置径向限位装置实现Δrsp≤Δrcr（Δrsp为通过径向限位装置约束的径向位移），避免该情况发生，如图6所示，此时限位爬坡角为

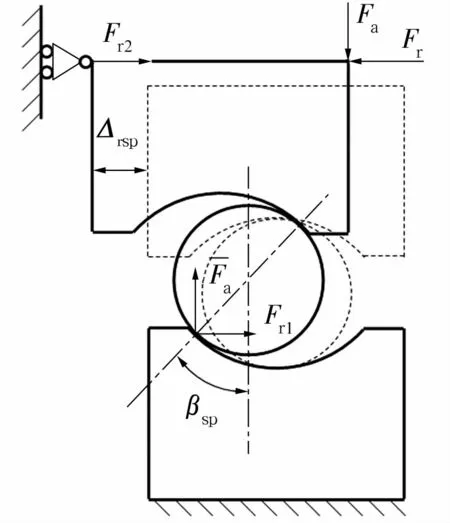
图6 限位爬坡角Fig.6 Limiting climbing angle

5 实例分析

以某大型动平台用推力球轴承为例分析，其主要结构参数见表1。

表1 轴承主要结构参数Tab.1 Main structural parameters of bearing

设置径向限位装置，当限位位移Δrsp＝3.0 mm时得到钢球的限位爬坡角为βsp＝48.59°。钢球最大接触载荷和应力为Qmax＝36.44 kN，σmax＝2 698.6 MPa。接触椭圆长半轴a对应的圆心角αa为13.72°。

6 结束语

图7 最大爬坡角随径向地震加速度的变化Fig.7 Variation ofmaximun climbing angle with radial seismic acceleration

当设置径向限位装置后，拟合得到钢球最大接触应力σmax随径向限位位移Δrsp的变化如图8所示。由图8可以看出，随限位位移的减小，相同爬坡角位置钢球的最大接触应力也将减小。另一方面，若设置的轴向限位过大，将不得不增加沟深h，从而增加轴承系统的设计难度和制造成本。故选择合适的限位位移需要统筹考虑设计、制造、公差等因素。

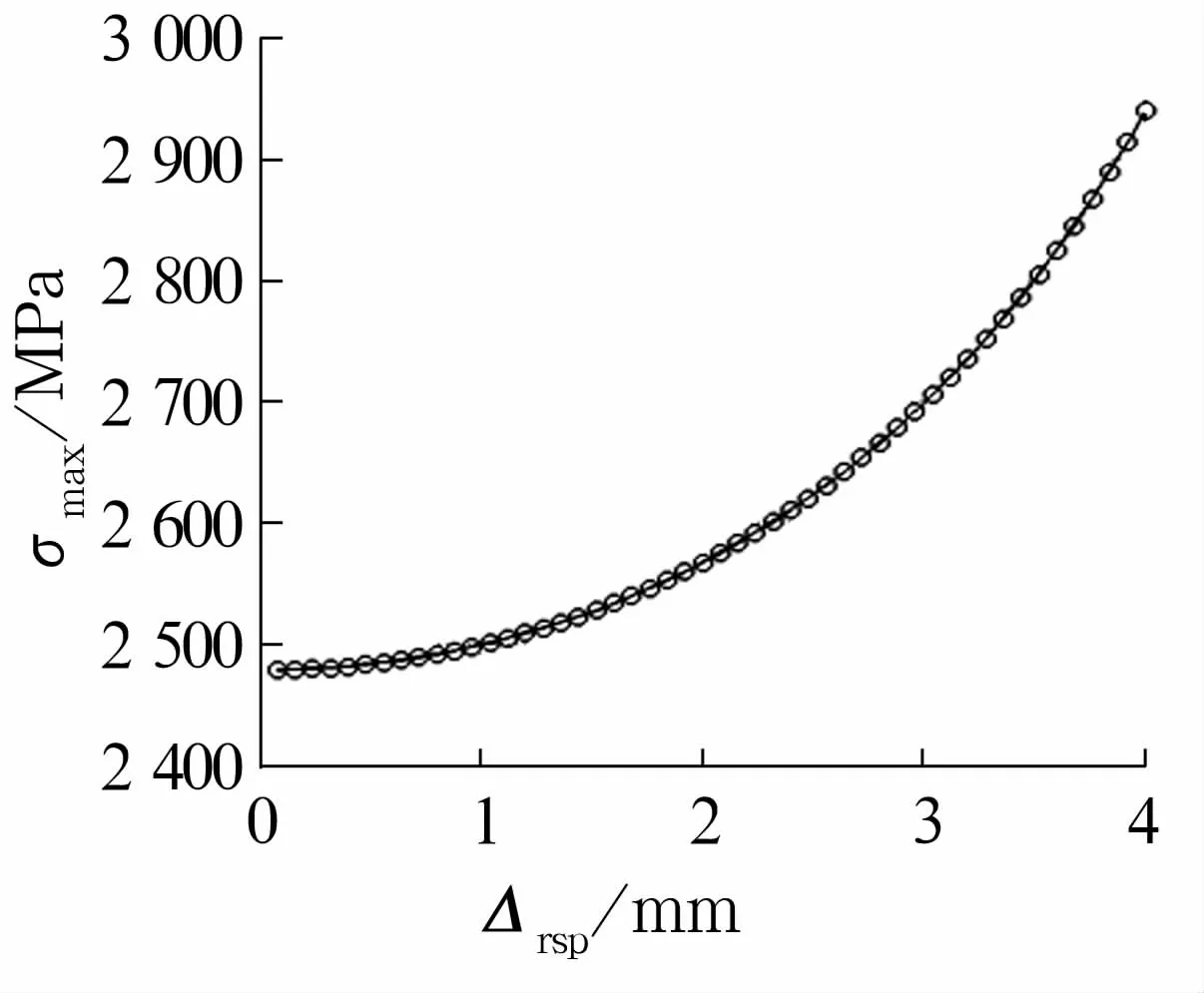
图8 钢球最大接触应力随径向限位位移的变化曲线Fig.8 Variable curve ofmaximun contact stress of steel ball with radial limiting displacement

对于开放型90°推力球轴承而言，随着径向地震载荷的增加，需要平衡的伴生轴向载荷也随之增加，安全爬坡角减小，钢球的最大接触应力增大，并可能出现钢球超出挡边的危险。为避免钢球超出挡边，减小钢球接触应力，提出了设置径向限位装置的方案，由于部分径向载荷由径向限位装置平衡掉，相同爬坡角位置的钢球接触应力明显减少，并给出了径向限位位移与钢球最大接触应力之间的关系。但文章仅分析了地震的径向和轴向载荷对该类轴承的作用，关于轴向和径向偏心引起的力矩影响以及工作温度的影响等尚未考虑。