基于Materials Studio氮化硅稳定性分析
2018-08-04廖燕玲钟志贤
廖燕玲,李 梦,钟志贤
(桂林理工大学机械与控制工程学院,广西 桂林541004)
氮化硅作为一种性能优异的陶瓷材料,具有密度低,硬度高,耐磨损,导热能力强等优异的物理性能以及抗氧化性,抗腐蚀性(尤其是除了HF外的无机酸)的高化学稳定性能等,因此在机械、电子等众多领域占据了重要的地位。
目前关于氮化硅的研究已取得了丰硕的成果,文怀兴等人[1]研究了氮化硅陶瓷轴承润滑技术,张传伟[2]研究了以球磨法在氮化硅表面制备MOS2模,处理氮化硅陶瓷表面还有离子注入法[2]、热喷涂法[3]、激光刻蚀技术[4]、溶胶-凝胶技术[5]等。徐彬[6]构建了β-Si3N4表面模型并对表面能进行计算,潘洪哲[7]采用超软赝势的方法分析了β-Si3N4的电子结构和光学性能,孙美[8]在不同压力下比较了氮化硅多个结构的性能。
本文采用Materials Studio软件中基于DTF的CASTEP模块对β-Si3N4进行建模和结构优化,采用模守恒平面波赝势方法对β-Si3N4模型的力学性质、动力学性质、热力学性质进行了计算和分析。
1 β-Si3N4建模与结构优化
β-Si3N4属于空间群 C6h,原胞(Si6N8)包含了 2个Si3N4分子,堆垛次序可以表示为ABAB…。本文应用Materials Studio8.0软件中的CASTEP模块对β-Si3N4进行建模和优化,优化内容包括晶格参数和原子坐标。优化前的晶胞参数为a=b=7.637A˚,c=2.922 A˚,α = β =90°,γ =120°,采用模守恒赝势方法,在倒易K空间中,平面波截断能通过收敛性测试可定为500eV,交换—关联能采用的是局部密度近似修正(GGA-PBE),通过测试可设定 K点网格:4×4×12.采用BFGS算法对β-Si3N4晶体进行结构优化,原子价电子中参与计算的为N 2S22P3、Si 3S23P2.
优化后的晶胞参数为 a=b=7.705627A˚,c=2.943081A˚,α = β=90°,γ =120°.图 1 为优化前后模型对比,Si-N键长发生变化,键角不变,结构优化后原子的坐标位置有所调整,优化过程按照最低能量方向进行,使得氮化硅结构更加稳定合理。
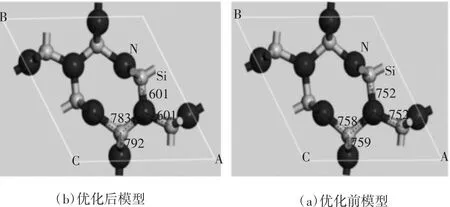
图1 β-Si3N4的结构模型
2 计算与分析
本文主要基于密度泛函理论的CASTEP模块进行建模计算,分析了β-Si3N4的力学性质、动力学性质、热力学性质。
2.1 力学性质
关于六方晶系,独立的弹性常数有5个,判断晶体的力学稳定性,根据Born-Huang标准要求:
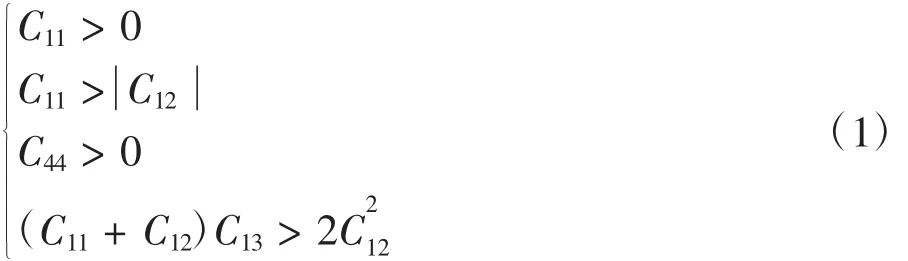
计算可得β-Si3N4的弹性常数为C11=370.031 GPa,C33=496.176 GPa,C44=97.130 GPa,C12=142.266 GPa,C13=81.183 GPa. 通过计算可知,β-Si3N4满足Born-Huang标准,可证明其稳定性。
表1为Voigt、Reuss以及Hill方法求得的体积模量和剪切模量的值,Pugh的经验判断表示,剪切模量与体积模量的比值(G/B>0.57)可预测材料性质为脆性,反之则为延性,β-Si3N4的G/B=0.58,为脆性材料。表2为杨氏模量和泊松比在各个方向上的值,表明了材料对单轴张量的抵抗变形能力,表中Ex=Ey,这是由于对称性的存在导致的,Ez比Ex的值约大160 GPa,这表明β-Si3N4在Z轴方向的抵抗弹性形变能力比在X轴更强。

表1 体积模量B(G Pa)和剪切模量G(G Pa)的值

表2 杨氏模量(G Pa)和泊松比在各方向的值
2.2 动力学性质
图2为β-Si3N4的声子谱,谱线分为0-20.8THz和24.5-34.5THz两部分。β-Si3N44的原胞有14个原子,理论上声子谱线一共有42个声子支,由3条声学支和39条光学支组成,声学支包括1条纵声学支LA和2条横声学支TA组成。在24.5~34.5 THz范围声子谱线交叠现象较为明显,该范围的原子相似振动状态较为严重,它们之间可能存在相互作用。声子谱中存在禁带,说明β-Si3N4的振动模不连续,此处对应的振动频率并不在晶体中发生。声子谱中无虚频,满足动力学稳定性。
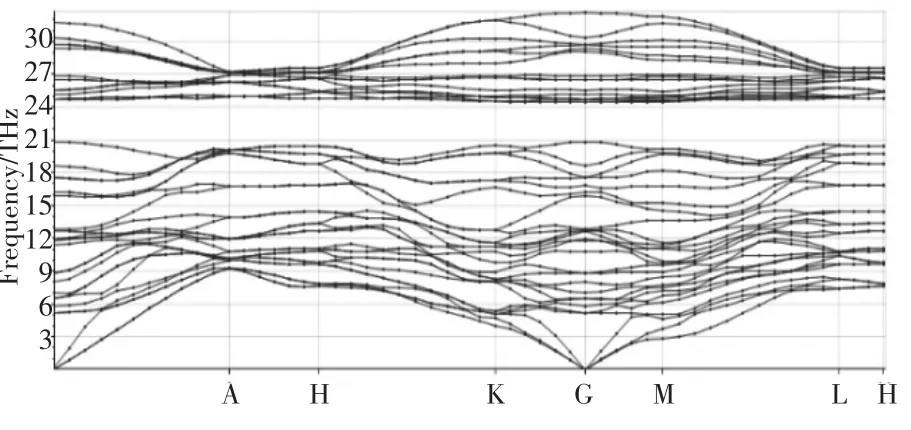
图2 β-Si3N4的声子谱
图3 的声子态密度(Full)中的间断与声子谱中的带隙宽度相对应。声子态密度图中存在尖峰,尖峰越明显,对应声子谱中的谱线越平缓,频率在25 THz处,晶体的晶格波振动最强烈。“Si”和“N”曲线为随机选取的单个原子的声子分态密度图。在0~16 THz区域Si和N原子态密度对总态密度贡献相似,16~20.8 THz区域Si原子的态密度贡献较多,24.5~34.5 THz区域N原子的态密度的贡献较多。

图3 β-Si3N4的声子态密度图
2.3 热力学性质
图4 中曲线①的纵坐标为温度与熵(S)的乘积,熵是体系中分子运动无序性量度。该曲线中温度与熵的乘积随着温度的增加而单调递增,斜率逐渐增大,曲线越来越陡。这是因为温度增加影响到晶体内原子的运动,温度上升越快,原子运动速率越大,原子运动剧烈。
曲线②的纵坐标为焓(H),焓是表征物质的系统能量的重要度量。

当温度上升时,粒子动能增加,体系中的内能U增加,分子热运动加剧,系统热膨胀现象明显,此时PV值也在增大,因此曲线②的焓与温度的关系曲线呈现上升趋势。
曲线③的纵坐标为自由能(F),自由能可以表述为热力学中体系内能中外做功的有用能量。

当温度升高时,内能升高,熵也增加,熵与温度的乘积远远大于内能的值,温度越高,其差距越大,自由能的值越低,且恒不大于0.
曲线④表现了热容量与温度之间的关系,热容量随着温度增加而递增,曲线的斜率由大变小,渐渐呈现饱和趋势,最终趋近于常数。温度较低时,固体的热容量是由晶格热振动和电子热运动共同作用,热容量增长较快,温度较高时,热容量主要是由晶格热振动决定,热容为=42 K,K是常数。

图4 温度影响曲线图
3 总结
本文主要选取了β-Si3N4作为研究对象,采用Materials Studio软件中的CASTEP模块来进行建模。计算得到了5个独立的弹性常数,根据Born-Huang标准,证明了β-Si3N4满足力学稳定性,并且计算了弹性模量,判断β-Si3N4为脆性材料以及在各个方向上的抵抗弹性形变能力;计算得到了声子谱和声子态密度,通过声子谱中不存在虚频判断其满足动力学稳定性,分析了单个原子的声子态密度对总态密度的贡献;计算得到了熵、焓、自由能以及热容量,分析β-Si3N4的热力学性质。
