穹顶结构的拓扑优化设计

梁智豪，余彦峰，吴伟辉，李湘勤

（韶关学院物理与机电工程学院，广东 韶关512005）

0 引言

穹顶是指一种悬垂的半球体空间或面积，在工程结构，尤其是建筑结构领域有着广泛的应用，如体育场、会议大厅、游泳池等采用穹顶结构。国内的天津博物馆、2008北京奥副产品会羽毛球馆和安微大学体育馆都是采用类似穹顶的结构。穹顶的形状、尺寸的设计一般是基于经验或工程设计计算，对经验的积累要求较高。穹顶结构作为建筑结构的构型，其受力特性的好坏影响着其性能的发挥，而结构的刚度或柔度是其受力特性的一个重要指标。提高结构的刚度或减小柔度是提高结构力学性能的重要举措，工程上通用的方法有增加截面尺寸、更换材料、优化结构设计等方法，对于优化结构设计最经典的方法是通过有限元分析，确定其危险部分，并进行强化设计，而这些方法都是建立在已有的设计构型上为某些性能的改善而进行的结构改型。从上世纪八十年代逐渐发展起来的拓扑优化设计，可以在设计之初为结构提供一种优化布局，从而使设计结构具有良好的性能。拓扑优化在工程结构领域被认为是一个很有应用价值的技术，从提出至今，已在建筑、机械和航天等领域广泛应用，如彭细荣等对高层建筑支撑体系进了拓扑优化尝试[1]，李湘勤等对力学传感器结构进行了拓扑优化设计[2]。对于穹顶结构优化设计较多的是对截面尺寸进行优化设计[3-5]，通过拓扑优化的方式直接获得穹顶结构材料布局的研究鲜有人问津。本文通过建立简化的几何模型并采用特殊的网格划分方式，采用拓扑优化技术获得在特定的材料用量限制情况下穹顶的结构材料优化布局，对拓扑优化结果进行结果提取并建立相应的三维模型，并根据材料用量限设计了两种用于对比的穹顶结构，通过力学试验，显示在相同力作用下，拓扑优化结构位移更小，证实了经拓扑优化设计得的穹顶结构材料布局具有更好的刚度。

1 问题描述

1.1 物理模型简化与网格划分

穹顶的简化的几何模型如图1（a）所示。设定穹顶的底部固定，顶部受压力作用，考虑到结构的对称性和周期性，以穹顶的四分之一为研究对象，利用有限元的思法进行网格划分，对于穹顶结构，其网格的划分是影响其能否获得对称且周期性的分析结果的关键因素，也就是说网格划分不保证有限元网格对称且周期性，拓扑优化时难以获得一个周期且对称的结构。因为四分之一穹顶结构外表面为三角形结构，无法直接用映射网格划分，为了获得对称、且周期分布的优化结果，外侧圆面采用顶部小面积自由三角形网格划分，其余外采用四边形映射网格划分，然后在厚度方向使用网格扫掠，最后得到棱柱网格与长方体网格共存的有限元网格模型，如图1所示。

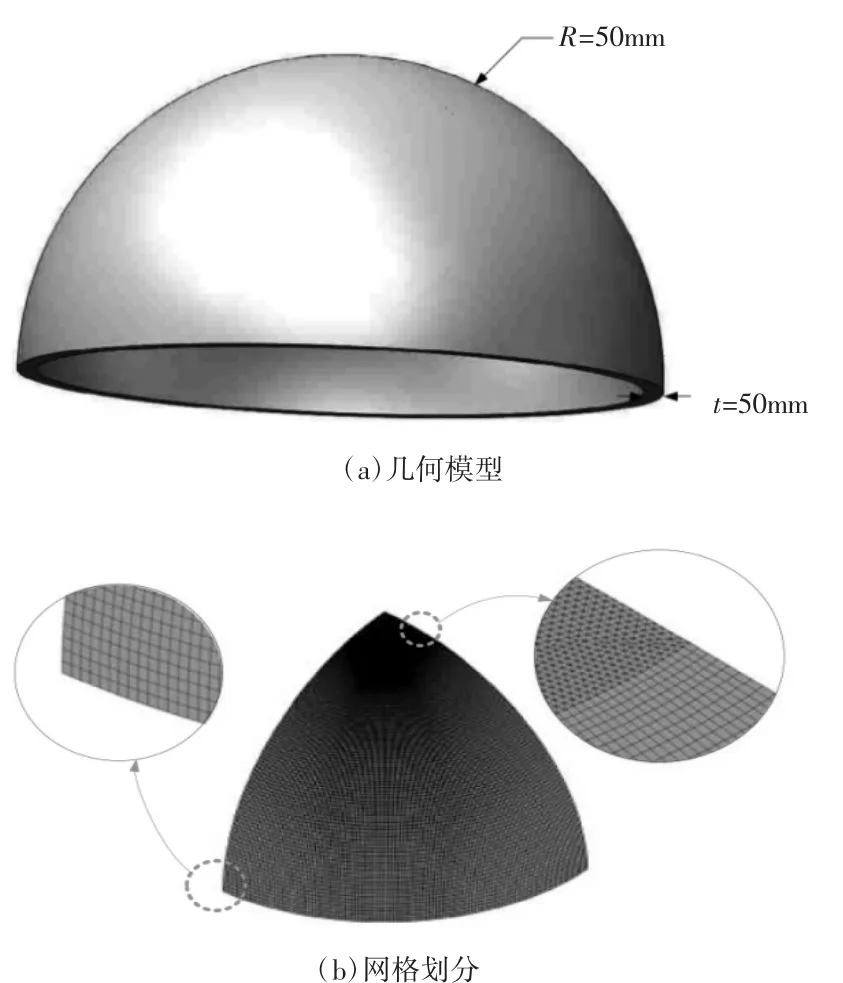
图1 穹顶几何模型与网格划分

1.2 拓扑优化数学模型建立

SIMP法[6，7]是拓扑优化中构建数学模型常用的一种基于材料密度的插值方法，其主要思想是通过定义每个单元具有独立伪密度值（一个介于[0，1]区间的数），并将单元的伪密度作为设计变量，由伪密度的值来表征单元的存在情况。SIMP法中单元i的单元刚度矩阵表示为

式中，ρi是单元i的伪密度；p是惩罚因子，本文p=3；k0为实材料的单元刚度矩阵。

以图1（a）穹顶简化模型为基础，在一定材料用量限情况下，以求获得最佳的结构力学性能，从而获得穹顶结构的材料优化布局，本文研究以在材料一定用量限下，穹顶结构刚度极大化为目标寻求材料最优布局。由于结构的刚度极大与柔顺度极小是一个等价问题，而对于材料用量限可以用结构的体积约束表述，所以以总体柔顺度极小为目标，以体积为约束的建立穹顶结构刚度极大化的拓扑化问题的数学模型建立，如下式：

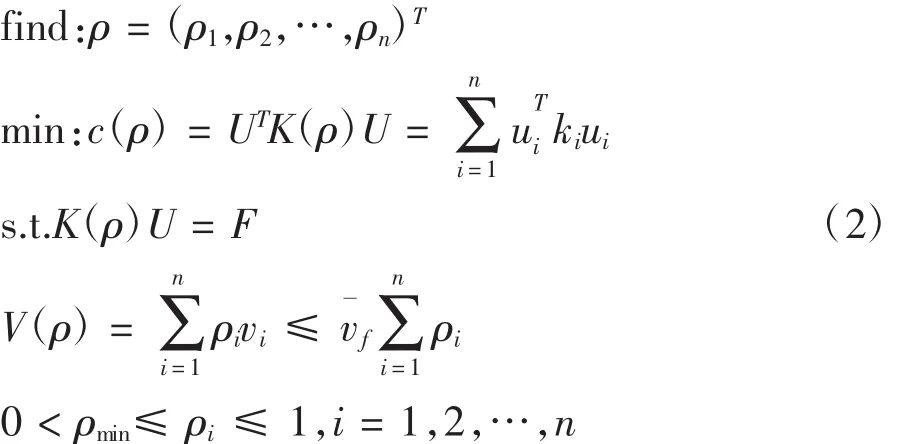
式中ρ为单元设计变量向量，K（ρ）为全局刚度矩阵，U为全局位移向量，F为全局载荷向量，ui为单元位移向量，ki为单元刚度矩阵，ui为单元体积，ρi为单元设计变量（伪密度）为体积约束分数，ρmin为单元设计变量最小值（用来避免全局刚度矩阵奇异，一般取值ρmin=0.001），n为单元个数。

2 敏度分析

拓扑优化一般需基于梯度来迭代更新设计变量向量ρ，因此需求得式所建立的数学模型目标函数对设计变量的敏度。引入拉格朗日乘子向量λ，由式（2）前两式构建拉格日方程如下：

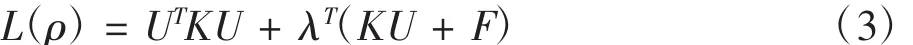
将式（3）对设计变量向ρ求导，并对极值有：

对于伴随方程有：

由式（5）求得 λ，并代入式（3），可求得公式（2）第一式目标函数对设计变量ρ的伴随敏度为：

优化问题（2）可通过优化准则法、二次线性规划法和移动渐近法等优化算法进行求解[2]。本文采用优化准则法实现对穹顶结构的拓扑优化设计。

3 优化设计结果

穹顶结构的拓扑优化几何模型和网格划分如图1所示，穹顶外径为100 mm，厚度3 mm；使用的材料密度ρ=7 850 kg/m；杨氏模量E=2.0×1011Pa.结构顶部最高点受压力作用，约束结构的底部端面，取体积约束分数为；目标函数为结构刚度极大化或柔顺度极小化。优化问题基于COMSOL3.5和COMSOL script3.5实现，两种体积约束下获得的拓扑优化结果如图2所示。

图2 拓扑优化结果

4 优化结构验证及分析

4.1 结构对比

针对图2所得的拓扑优化结构，提取材料布局，并构建全穹顶结构模型，如图3所示。

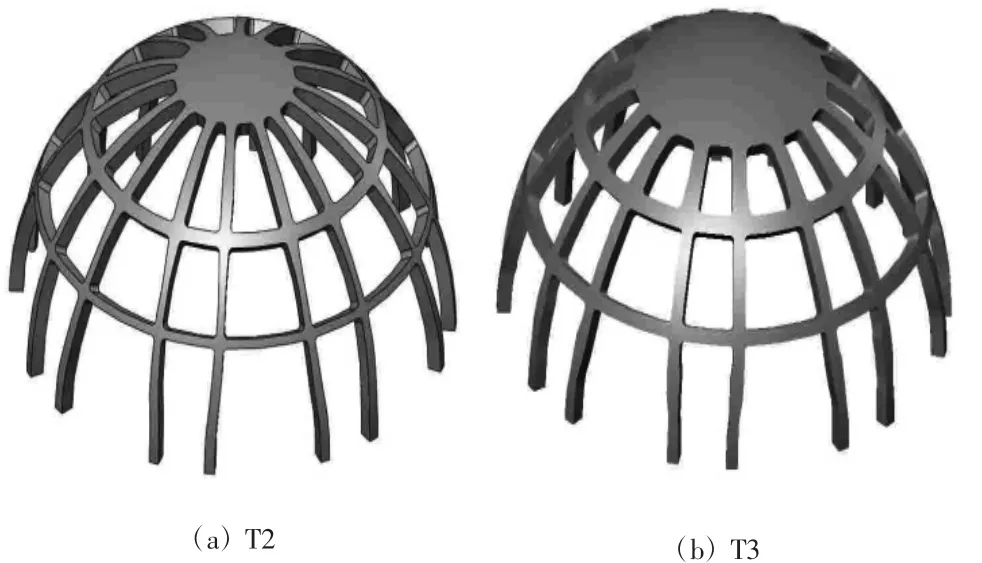
图3 拓扑优化材料布局结果提取

图3 （a）穹顶结构（用T2表示，表示在体积约束分数为0.2时得到的优化结果）对应拓扑优化结果图2（a），图 3（b）穹顶结构（用 T3 表示，表示在体积约束分数为0.3时得到的优化结果）对应拓扑优化结果图2（b）。为了对比拓扑优化结果穹顶结构材料布局的力学性能，设计了两种杆宽一致的穹顶结构，如图4所示，图 4（a）穹顶设计结构（S2）的体积与图 3（a）穹顶拓扑优化结构（T2）体积接近，所有杆宽为3.6 mm；图 4（b）穹顶设计结构（S3）的体积与图 3（a）穹顶拓扑优化结构（T3）体积接近，所有杆宽为4.4 mm，两种穹顶结构纬向围杆离穹顶底端面距离相同，经向围杆数量相同，且周向均布。

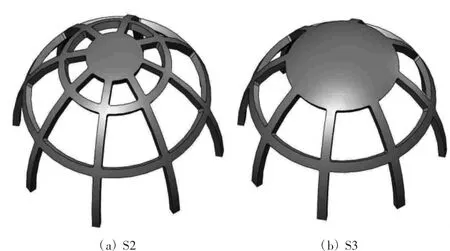
图4 穹顶设计结构

4.2 打印制作

利用太尔时代的UP2产品采用ABS材料打印制作，为了减少结构内部的空洞结构，参数设置中采用最0.2 mm的层片厚度与最精细填充方式，得到的四种穹顶结构实物如图5所示。

图5 穹顶结构3D打印实物

4.3 受力试验

对四种结构分别用电子天秤称量，获得各自打印制作出来后实际的质量。考虑到位移极小与刚度最大的等价性[8]，试验时，在穹顶最高点加载压力，以20 N为增量连续加载，测试其负载与位移的关系，最终得到图5四种结构的负载与位移关系如图6所示，其中图中每条数据线末端结点为结构发生断裂前的近似位移与受力关系。

图6 力学试验

根据零件荷载与位移的比值为刚度，刚度的倒数为柔度，对于图5四种穹顶结构，取各数值点力与位移比值的平均值为穹顶刚度为了便于比较并剔除结构屈服后的受力试验数据，取一定受力区间Fˆ内穹顶刚度作比较，假定刚度提高系数δ为拓扑结构和设计结构的差值与设计结构的比值，图5四种穹顶结构的结构刚度对比如表1所示。

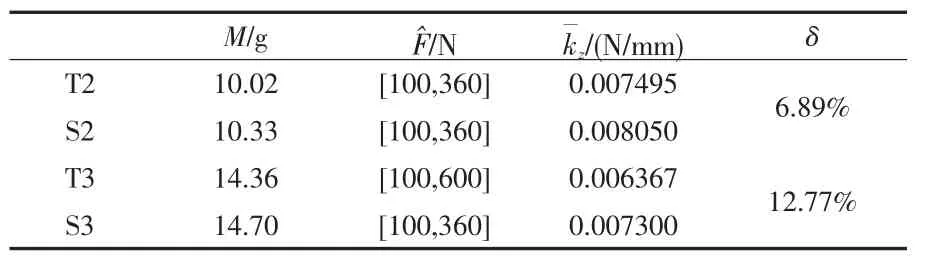
表1 四种穹顶结构受力试验数据对比表

从表1可知，拓扑优化布局的质量虽轻于设计布局的质量，在结构屈服前，经拓扑优化获得的穹顶结构的材料布局的刚度值明显小于设计布局，对于体积分数接近＝0.2的拓扑结构与设计结构因材料布局较为相似，得到的刚度提高较小，而对于＝3，刚度提高较为明显，达到了12.77%.对比结果，显示出拓扑优化获得的杆结构较设计结构的杆细，使得相比设计布局，总承载能力有所下降。

5 结论

本文针对建筑工程中的穹顶结构提出了应用拓扑优化方法进行优化设计的方法。主要结论如下：

（1）结合建筑工程中穹顶结构的力学性能要求，以简化的穹顶几何模型构建用于拓扑优化的物理模型，为获得对称且周期性的结果，采用自由网格与映射网格相结合的方式使得网格基本呈现对称、周期分布，这种网格划分方式有力地保证了在穹顶结构有限元分析时获得对称且周期性的结果；

（2）应用基于SIMP插值方法，建立以刚度极大或柔顺度极小的拓扑优化数学模型，推导目标函数对设计变量的伴随敏度，利用优化准则法进行拓扑优化，获得了在两种体积分数约束下的拓扑优化构型，针对拓扑优化构型的材料分布进行结构提取，构建对应的三维几何模型。最终的优化结果显现出材料分布规律明显，便于进一步的形状优化或制作。本文研究的只针对刚度极大化问题，结构受力单一，而穹顶结构实际性能要求复杂、工况繁多，但依然可以通过多目标函数处理方法进行拓扑优化设计，但此时模型的非线性增强，不利于获得材料分布有规律且整齐的结构。

（3）以与拓扑优化构型相近的用料量设计两种杆系等宽的穹顶结构，针对四种穹顶结构采用3D打印制作实物模型。采用对穹顶顶部加压，以验证拓扑优化结构与设计结构的力学性能差别。对比试验结果，实例展现经拓扑优化获得的穹顶结构刚度分别提升6.89%和12.77%.所以，应用拓扑优化设计穹顶结构的构型，可以有效的弥补基于经验设计的不足，也为穹顶结构的形状设计提供有力借鉴。