基于主成分分析和熵值法的智慧城市发展现状研究

张 宁，盛 武



基于主成分分析和熵值法的智慧城市发展现状研究

张 宁，盛 武

（安徽理工大学 经济与管理学院，安徽 淮南 232001）

为提高国内智慧城市建设水平，结合现有的智慧城市评价指标与各智慧城市发展的实际情况，选用经济水平、环境治理、基础设施等5个一级评价指标，运用主成分分析法和熵值法对北京、上海等10个样本城市进行综合分析，找出影响智慧城市建设的关键因素以及各城市的智慧城市建设水平。结果表明：影响智慧城市建设的因素众多，其中，经济实力、人才支撑、科技创新能力是重要影响因素；我国智慧城市建设存在发展水平不均衡，不同城市之间发展差异较大的现象；北京、上海、广州、深圳在智慧城市建设中已取得显著成效。

智慧城市；熵值法；主成分分析法；评价指标

智慧城市是指将云计算、物联网等信息技术与城市建设管理相结合，通过深度挖掘、整合数据获取与城市建设有关的信息，根据所获得的信息对包括民生、基础设施、环境等在内的各种活动作出响应。[1]“智慧城市”一词首次出现在1990年美国旧金山举行的一次以“智慧城市、全球网络”为主题的国际议会上。[2]经过近30年的发展，“智慧城市”已成为城市规划建设中的重要战略目标。近年来，不断成熟的智能化技术给智慧城市建设提供了可靠的技术支撑，使国内智慧城市建设开展得如火如荼。截止2017年，我国开展智慧城市试点工作的城市已超过500个。[3]

影响智慧城市建设的相关因子是衡量智慧城市建设的重要维度，对激发智慧城市发展潜力、提高智慧城市建设水平起着至关重要的作用，因此，构建智慧城市评价指标，分析各指标在不同城市的发展水平已成为学术界研究的热点之一。作为全球首个提出“智慧城市”概念的企业，IBM主张从城市服务、市民生活、商业水平、交通环境、通信技术、供水情况、能源等7个层面构建智慧城市评价指标。[4]维也纳理工大学研究小组构建了智慧市民、智慧生活、智慧治理、智慧经济、智慧交通、智慧环境等6个一级智慧城市评价指标。[5]中国的李健等认为可以从发展水平、信息通信设施和实际应用效果等3个方面评价智慧城市建设水平。[6]王振源等利用AHP构建了智慧基础设施、公共管理情况、公共服务、公共支撑体系等4个一级评价指标体系。[7]以宁波市智慧城市规划标准发展研究院为主的研究团队拟定了宁波市智慧城市评价体系，指出从智慧基础设施、智慧治理、智慧民生、智慧产业、智慧民众、智慧环境等6个方面评价智慧城市发展水平。[8]

综合分析国内外现有研究成果可以发现，虽然国内针对智慧城市评价体系的研究颇多，但从主观和客观两个角度对各影响因素进行综合评价的研究文献甚少。因此，本文以我国智慧城市发展现状为客观依据，通过构建合理的评价体系，综合利用主成分分析法和熵值法对智慧城市建设中的主要影响因素进行对比分析，全面了解影响智慧城市建设的各种因素，并对各智慧城市的发展潜力进行综合评价，以期为我国智慧城市建设提供可靠的理论依据，避免智慧城市建设过程的盲目性和从众性。

一、 智慧城市发展评价体系构建

（一） 评价指标选取

智慧城市建设受多种因素的影响。本文在遵循可操作性、可靠性、可持续性、定性和定量相结合原则[9]的基础上，综合考虑国内外的评价指标，结合各城市发展现状和实际情况来确定评价体系。经过反复筛选和推敲，构建出合适的智慧城市建设评价指标体系，涵盖了经济水平、环境治理、基础设施、科技创新、人才支撑等5个一级评价指标，其中包含了18个二级指标（表1）。

表1　智慧城市建设评价指标

（二） 样本数据来源

依据我国城市的发展现状和实际规划情况，本文选取了北京、上海、广州、深圳等4个一线城市以及武汉、杭州等新一线和合肥等二线城市为样本进行实证分析。数据来源主要以各样本城市官方网站上公布的2016年统计年鉴为主，相关政府部门的工作报告以及互联网数据为辅。

（三） 研究方法

研究方法上，选取主成分分析和熵值法两种数据分析方法进行分析。主成分分析法可以消除各指标间的相关性，熵值法具有很强的数据客观性，用这两种模型进行分析可以兼顾主观和客观因素，[10]从而提高分析结果的可靠性和科学性。

二、 主成分分析评价过程

（一） 主成分分析法基本原理

主成分分析法是在保证信息受到最小损失的前提下，借助降维思想，将与客观问题相关的多个指标用少数几个综合指标来代替，将复杂的问题简单化。[11]本文借助主成分分析，通过特征值、方差贡献率找出影响智慧城市建设的关键指标，在此基础上，计算各样本城市在主成分上的综合得分，从而得出各城市的智慧城市建设水平。其基本原理如下：

（1）设有个评价对象，个评价指标，构成一个×阶原始矩阵

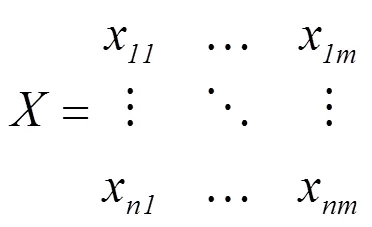
（2）矩阵数据标准化。对数据进行标准化，可消除单位及量纲不同而产生的不合理现象。本文采用的标准化方法为：

（3）计算标准化矩阵X*的相关系数矩阵：

（4）求矩阵R的特征值和特征向量：令

（5）确定主成分的个数：根据主成分选取原则，一般将累计贡献率大于85%的成分提取为主成分。

（二）主成分分析结果

在对原始数据进行标准化处理基础上（表2），运用SPSS 21.0对样本数据进行分析，得到主成分特征值、方差贡献率和累计方差贡献率（表3）。

表2 标准化数据矩阵

变量北京上海广州深圳天津武汉杭州重庆合肥西安 X11.240 81.577 80.418 70.411 30.195 5-0.606 6-0.687 10.176 1-1.363 8-1.362 7 X21.672 21.519 40.517 70.213 9-0.050 4-0.673 5-0.576 2-0.305 5-1.243 1-1.074 6 X31.278 20.787 60.928 50.542 8-0.650 3-1.030 00.658 7-1.334 7-1.362 70.182 1 X41.814 0-0.995 3-0.078 00.839 3-1.396 6-0.694 3-0.393 3-0.364 61.126 00.1428 X5-1.139 90.673 30.588 91.159 50.943 40.752 6-1.163 5-0.940 70.423 4-1.296 9 X6-1.629 7-0.527 4-0.136 20.752 81.464 01.001 70.183 80.752 8-0.918 5-0.943 4 X70.516 30.608 5-1.189 30.608 5-2.065 10.608 50.608 50.608 50.608 5-0.912 7 X80.034 4-0.236 3-0.041 9-0.819 30.202 90.136 6-0.514 12.637 4-0.771 8-0.627 9 X92.428 70.285 5-0.479 20.282 8-0.181 9-0.501 2-0.279 70.329 2-1.424 0-0.460 3 X101.586 21.805 30.301 20.146 8-0.401 0-0.380 6-0.866 7-0.211 8-1.150 1-0.829 5 X110.026 31.035 10.154 41.011 8-1.180 40.110 0-0.174 81.469 7-1.598 8-0.853 3 X120.564 80.564 80.547 70.285 50.564 8-1.810 70.564 80.199 0-1.950 30.469 7 X130.435 80.435 80.435 80.435 80.435 80.435 80.435 8-2.581 1-0.905 00.435 8 X142.222 00.974 6-0.633 80.762 7-0.358 7-0.862 8-0.366 8-0.467 3-0.855 7-0.414 2 X151.010 30.098 2-0.301 20.369 5-0.516 5-0.937 3-0.483 5-1.334 7-1.049 52.251 1 X16-0.080 0-0.380 91.551 5-1.886 7-0.384 11.165 1-0.690 1-0.364 6-0.435 10.745 5 X172.135 90.915 0-0.608 50.832 80.009 9-1.023 2-0.612 2-0.940 7-0.915 8-0.427 3 X182.249 80.781 30.216 9-0.024 0-0.323 3-0.187 6-1.336 1-1.048 5-0.482 30.154 0

表3 主成分特征值、贡献率及累计贡献率

从表3可以看出，前5个主成分的累计方差贡献率大于85%，说明前5个主成分保留了原始变量的主要信息，因此可以用这5个成分代替所有变量来反映我国智慧城市发展现状。在确定主成分之后，利用SPSS21.0得到主成分因子载荷矩阵（表4）。从表3、表4可以看出，主成分1的贡献率最大，是智慧城市建设最重要影响因子。它在X2（第三产业生产总值）、X9（民用机动车数量）、X10（轨道交通总长度）、X14（R&D经费支出）、X17（R&D人员）指标上均有较大载荷，占据的指标数量多、类型丰富，因此可以认为主成分1是影响智慧城市建设的综合性因子。主成分2的贡献率为16.378%，是影响智慧城市建设的次要因子，它在X6（城市污水集中处理率）、X8（高速公路长度）、X11（宽带用户数）指标上具有较大因子载荷，其中X8、X11为基础设施指标体系，因此可以认为主成分2是影响智慧城市建设的基础设施建设性因子。主成分3的贡献率为12.939 9%，在X5（一般工业固体废物综合利用率）、X13（用水普及率）指标中的因子载荷较大。主成分4在X5（一般工业固体废物综合利用率）、X7（生活垃圾无害化处理率）、X16（高等学生在校数）上载荷较大，且X5和X7均为环境治理指标，因此可以认为主成分4是智慧城市建设的环境治理性因子。主成分5的贡献率最低，主要体现在指标X12（全社会气化率）、X16（高等学生在校数）、X18（第三产业就业人员比例）上，其中X16和X18均为人才支撑性指标，故认为主成分5是建设智慧城市中重要的人才支撑因子。

最后，分析主成分得分系数矩阵，对各样本城市的主成分得分情况进行评价（表5），客观地反映出各智慧城市发展水平。表5显示智慧城市建设水平较高的城市有北京、上海、广州、天津、深圳。与国内其它城市相比，这5个城市在科技创新、人才素质、经济实力等方面均处于领先地位，这在某种程度上为智慧城市建设提供了坚实的物质和技术支撑，因此各城市在进行智慧城市建设过程中，应向这些城市学习，注重发展科技、人才和经济实力。此外，从主成分综合得分来看，除北京、上海、广州、天津、深圳等5个城市的综合得分为正值外，其它5个城市得分均为负值或0，这说明目前我国各智慧城市发展水平不均衡、不同城市之间尚存在较大差距。

表4 主成分因子载荷矩阵

表5　各主成分得分及排名情况

三、熵值法分析评价过程

采用主成分分析法可以总结出影响智慧城市建设的主要因子。但是，由于主成分分析忽略了自变量和因变量之间的关系，主观性较强，因此，分析结果缺乏一定的说服力。为此，利用熵值法确定各个成分的权重，从客观角度对智慧城市建设水平进行评价。

（一） 熵值法基本原理

作为判断指标离散程度的方法，熵值法通常借助系统无序化程度来度量不同因素对评价对象的影响程度。在熵值法中，指标的作用取决于该指标所占权重，权重越大，作用越大，反之相反。由于指标的权重完全由数据本身的关系决定，因此评价结果具有很强的客观性。[12]与主成分分析法不同，熵值法着重计算了各评价指标的权重，从而得出影响智慧城市建设关键指标因素，在此基础上，对各样本对智慧城市建设水平进行排序、分析。熵值法计算步骤为：

1. 定义原始矩阵

2. 数据标准化

3. 计算第j项指标在第i个评价对象上的指标权重

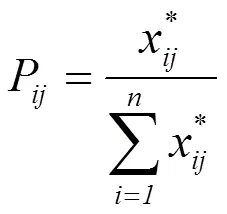
4. 计算第j个指标的熵值

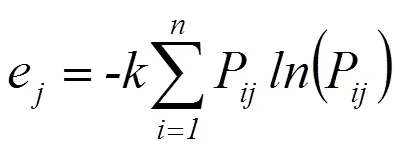
5. 计算第j个指标的差异系数

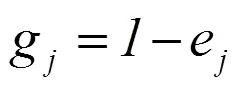
6. 计算第j项指标的权重

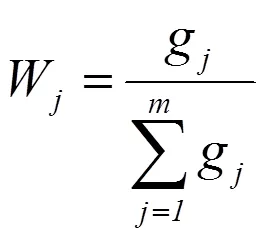
对第i个城市综合评价

（二） 熵值法分析结果

通过式（5）－（10），对样本城市数据进行计算，得出各评价指标权重。在此基础上，利用公式（11）计算出各城市在一级指标上的综合评价值和各城市综合得分及排名情况（表6）。从表6可以看出，各智慧城市的整体发展水平排名与经济发展、人才支撑两项指标的排名相近，这表明经济发展水平和人才储备是影响智慧城市建设的主要因素。此外，与其他城市相比，北京、上海、深圳、广州的智慧城市水平位居前列，说明这些城市在智慧城市建设中取得了较高成效。从横向指标来看，排名前两位的北京、上海在经济发展、基础设施、科技创新、人才支撑等各方面均处于优势地位，这从深层次上表明了在智慧城市建设过程中，不能只注重某一方面的影响作用，要充分发挥各影响因素之间的协调作用，兼顾其它因素在智慧城市建设中所起的作用。

表6　智慧城市指标评分及排名

四、结论

通过建立智慧城市评价指标体系，利用主成分分析和熵值法从主观和客观两个角度对各指标在智慧城市建设中所起的作用进行综合分析评价，得出以下结论：

1）在影响智慧城市发展水平的众多因素中，经济实力、人才支撑、科技创新能力是重要因素。因此，在智慧城市建设过程中，政府应注重经济发展，将物联网、大数据等信息技术与科技创新紧密结合，重视人才培养，大力引进优秀人才，积极采用产、学、研相结合的发展模式，为智慧城市建设奠定坚实的物质基础，从而不断提高智慧城市建设水平。

2）主成分分析结果显示，智慧城市建设水平排名前5的城市分别为北京、上海、广州、天津、深圳，通过熵值法得出的结果为北京、上海、深圳、广州、杭州5大城市。综合分析可以发现，北京、上海、广州、深圳的经济实力较强，城市基础设施完善，科学技术和科技创新能力位居全国前列，在智慧城市建设中处于领先地位。重庆、西安、合肥等城市由于经济发展水平、科技创新能力相对于北京等城市较为落后，在智慧城市建设过程中尚处于探索期。

3）目前，国内各智慧城市建设发展水平不均衡、不同城市之间存在较大的悬殊。为缩小各城市之间的智慧城市建设差距，各个城市应积极向国内发达城市学习，不断进行自我完善，逐渐形成各具特色的智慧城市发展模式。此外，在智慧城市建设过程中，除了关注影响智慧城市建设的关键因素外，还要兼顾其它因素在智慧城市建设中所起的作用，充分发挥各因素之间的协调作用。各城市要不断提高城市环境治理水平，注重城市的可持续发展，为打造安全、绿色的智慧城市打下坚实基础。

[1] 刘笑音, 郑淑蓉. 基于主成分方法的我国智慧城市发展潜力评价[J]. 科技管理研究, 2013(22): 75-79.

[2] 智慧城市网. 浅析近些年中国智慧城市发展趋势[EB/OL]. [2017-10-20]. https://www.zhihuichengshi.cn/XinWenZiXun/ 36704.html.

[3] 智慧城市网. 中国智慧城市试点已超过五百个[EB/OL]. [2017-11-20].https://www.zhihuichengshi.cn/Planning/ZhiHuiYingYong/37324.html.

[4] IBM商业价值研究院. 您的城市有多智慧？——帮助城市衡量进步[OR/OL]. [2012-12-18].http://wenku.it168.com/d_ 000560879. shtml.

[5] Rudolf Giffinger. Smart Cities Ranking of European Medium-sized Cities[R]．, 2007,10.

[6] 李健, 张春梅, 李海花．智慧城市及其评价指标和评估方法研究[J]. 电信网技术, 2012(1): 1-5.

[10] 孙斌, 严波, 尚雅楠. 基于系统动力学的包头市智慧城市评价体系研究[J]. 城市发展研究, 2016,23(8): 6-11.

[11] 龚炳铮．智慧城市评价指标和评估方法的探讨[J]. 办公自动化, 2015(02): 38-42.

[12] 赵丽, 付梅臣, 张建军. 乡镇土地集约利用评价及驱动因素分析[J]. 农业工程学报, 2008,4(2): 89-94.

[13] 韩晓明, 王金国, 石照耀. 基于主成分分析法和熵值法的高校科技创新能力评价[J]. 河海大学学报, 2015,17(2): 83-88.

[14] 汪冬华. 多元统计分析与SPSS应用[M]. 上海: 华东理工大学出版社, 2010.

[15] 王富喜, 毛爱华, 李赫龙, 等. 基于熵值法的山东省城镇化质量测度及空间差异分析[J]. 地理科学, 2013,33(11): 1323-1329.

Research on the Situation of Smart City Based on Principal Component Analysis and Entropy Method

ZHANG Ning, SHENG Wu

（School of Economics and Management, Anhui University of Science and Technology, Huainan, Anhui 232001, China）

It is to improve the level of the domestic wisdom of urban construction, combination with the existing evaluation index of smart city and the actual situation of the development of smart cities, building economic level, environmental governance, infrastructure and other five first-class evaluation indicators. Using the principal component analysis and entropy value method, a comprehensive analysis is made on 10 sample cities such as Beijing and Shanghai to find out the key factors influencing a smart city construction and the level of smart city construction in each city. The results show that: there are many factors affecting the construction of a smart city, among which, the economic strength, talent support and technological innovation ability are important influencing factors. The development of smart city in China is unevenly developed and there are large differences in development among different cities. Currently，Beijing, Shanghai, Guangzhou and Shenzhen have achieved remarkable results in the construction of smart cities.

smart city; entropy value method; principal component analysis; evaluation index

2018-05-02

国家自然科学基金项目（71371014）；安徽高校省级自然科学研究重点项目（KJ2016A205）；安徽省哲学社科规划项目（AHSKY2016D20）

张宁（1992-），女，河南漯河人，硕士研究生，主要从事区域发展与信息管理研究；盛武（1969-），男，安徽淮南人，副教授，博士，主要从事区域发展与信息管理、大数据分析与应用研究

F 291.1

A

10.3969/j. issn. 2096-059X.2018.03.006

2096-059X(2018)03–0030–06

（责任编校：贺常颖）