3D打印机运动学仿真分析①

(安徽机电职业技术学院,安徽 芜湖 241000)

0 引 言

3D打印技术(3D print technology)，是近几年来制造领域迅速展开和推广的一个重大技术成果，是快速成型技术(Rapid prototyping manufacturing, RPM)的一种。它是一种以数字模型文件为基础，运用粉末状金属或塑料、树脂等可粘合材料，通过逐层打印的方式来构造物体的技术。目前，3D打印技术可广泛用于医疗、航空航天、工业制造、汽车、消费品等领域。

并联臂式3D打印机结构简单、传动效率高，速度快，打印过程平稳，精度高，易于实现实时控制以及打印空间大等优点。

1 并联臂式3D打印机系统描述

图1为某品牌三角形并联臂[1]式3D打印机结构在典型工作位置的三维造型，其打印喷嘴处于机构中心位置。该3D打印机结构主要由铝合金横梁、并联臂、导轨、滑块、工作台面、底座横梁、送料步进电机、冷却风扇以及打印喷头组成。其中三组并联臂的一端通过球面副连接到对应滑块上，滑块通过电机驱动的同步带在导轨上进行上下运动。三组并联臂的另一端通过球面副连接到打印喷头上，并联臂是以三组平行四边形机构与移动副相联。该3D打印机工作空间大，移动速度快，通过三个步进电动机驱动三个同步带，再由同步带带动导轨组件三个滑块上下位置竖直移动，三个滑块协调配合让打印喷头实现3D实体的逐层打印。

该种并联臂式3D打印机使用了虎克铰作为传动运动副连接着并联臂与滑块和打印喷头，其优点是自由度高，传动效率高，但存在着易磨损和难修理的缺点。因此该种并联臂式3D打印机要求虎克铰具有一定的耐磨损能力。从该并联臂系统的结构及运动学计算着手，使用ProE中的运动学仿真以及ANSYS Workbench中的动力学仿真，分析计算了该系统打印喷头工作状态下的位置、速度以及加速度数值结果，同时计算了该工作状态下虎克铰上最大受力载荷。根据阿查得线磨损率计算公式，分析推算了该系统中虎克铰的线磨损率。

根据打印机各结构的功能要求，把送料步进电动机、冷却风扇和工作台面等简化，建立该并联臂式3D打印机的结构模型简图如图2所示：

2 机构自由度的计算

在空间机构中，每个完全不受约束的物体都有6个自由度，每个运动副都有其约束。本结构中，有1个机架，3个滑块，6根连杆，1个打印喷头，共有11个构件。3个滑块有3个移动副，3个自由度；连杆与滑块、连杆与打印喷头间共有12个球面副，36个自由度，故该3D打印机共有15个运动副，39个自由度。根据并联机床Kutzbach-Grubler[2]公式进行自由度计算

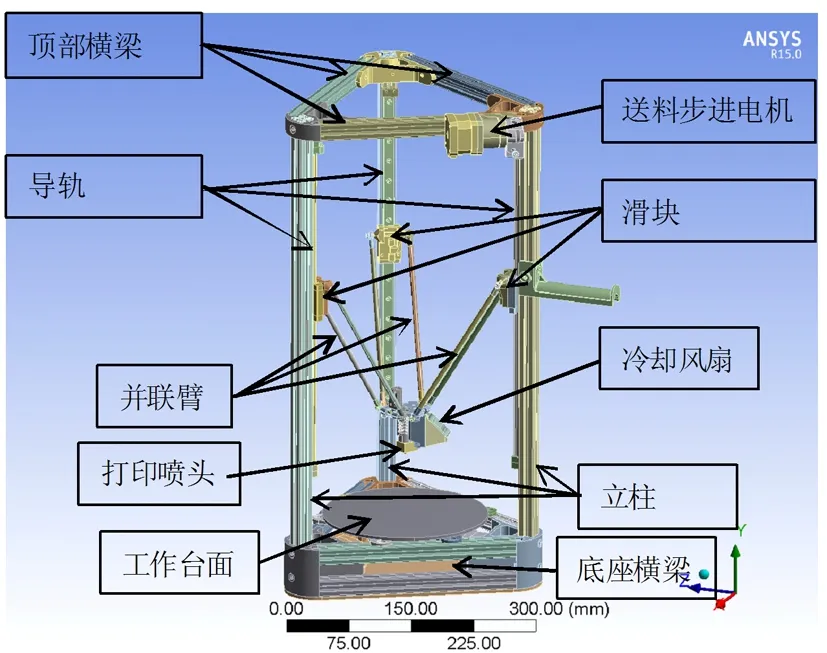
图1 某并联臂型3D打印机结构

图2 某并联臂型3D打印机简化结构

(1)

式中:n为构件总数；g为运动副总数；fi为各运动副的自由度数

其中，由于连杆两端的球面副均绕自身轴线运动，故此处有6个局部自由度。故由公式1推导出此结构的自由度计算公式如下所示：

(2)

式中fp为局部自由度。

把各个数值代入公式(2)后知，自由度F′ =3，即本3D打印机的自由度数为3，正好与本3D打印机的三个步进电机驱动相符合。

3 运动学正反解分析

该3D打印机的底座和顶部横梁结构均为等边三角形，导轨均平行且垂直布置，打印喷头随着滑块的移动而运动，打印喷头在空间位置上可以达到任意位姿，打印喷头在连杆作用下始终处于竖直位置，故可把打印喷头看成一个可以在空间任意位置移动的动平台。根据打印机的结构，建立该并联臂式3D打印机的坐标系如图3所示。

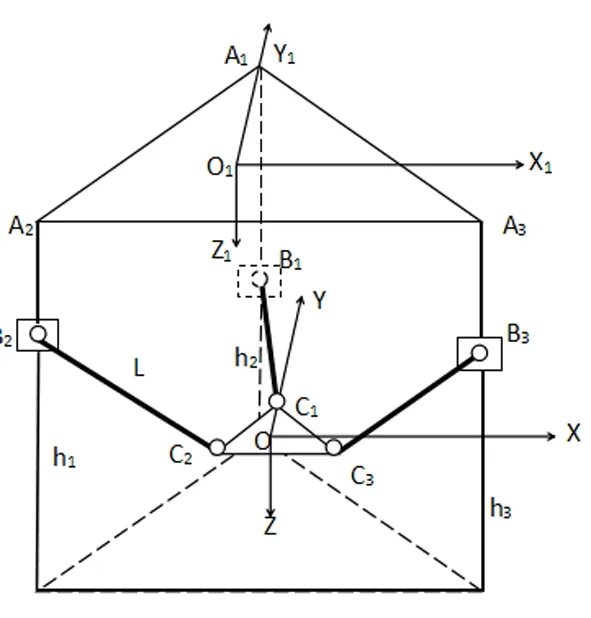
图3 某并联臂型3D打印机的空间坐标系

假设某型3D打印机的顶座横梁正三边形的内接圆半径为R，动平台的内接圆半径为r，并联臂连杆的长度为L，以打印机顶座横梁正三边形的内接圆中心点为坐标原点O1，建立坐标系O1-X1Y1Z1，假设各导轨运动到图3所示位置，A1B1、A2B2、A3B3的高度分别为h1、h2、h3，打印机喷头的坐标为O-XYZ，打印机喷头的位置随着各导轨运动而发生改变。假设滑块运动的位移AiBi=[0,0,li]T(i=1,2,3),建立的支链简图如图4所示：

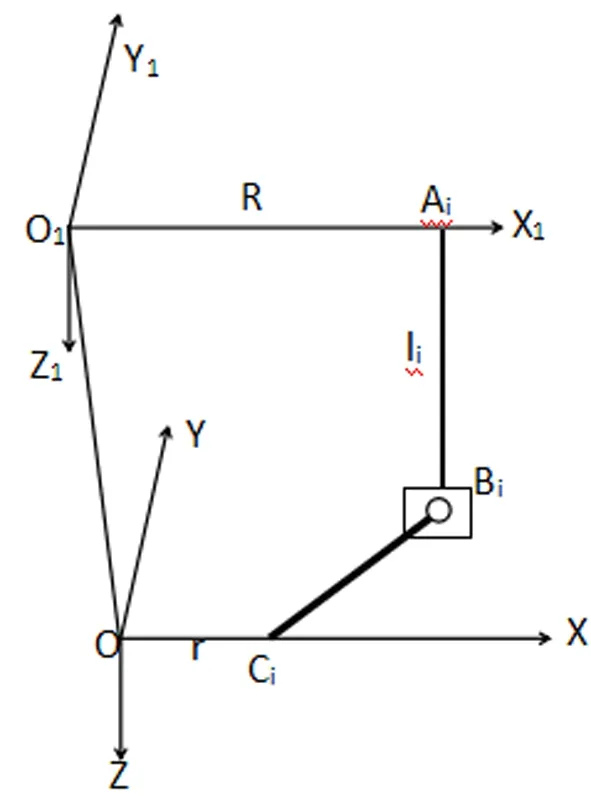
图4 某并联臂型3D打印机的支链简图

(4)

(5)

根据空间向量的运算知，向量O1Bi=O1Ai+AiBi(i=1,2,3),则

(6)

动平台相对于顶座横梁移动的坐标为(x,y,z)，即O1O=[x,y,z]T,向量O1Ci=O1O+OCi，则

(7)

由于三组并联臂的臂长固定，则BiCi2=l2，代入坐标后得，

(8)

设R-r=c，由于静平台在上，动平台在下，故li>z，解方程(8)得导轨运动方程的反解方程如下所示：

(9)

结构中运动学反解是在打印机顶座横梁中心点为定坐标系的坐标，求解三组导轨滑块的位置。并联机构的正解是用解析法或数值法解多元方程组，从而得到打印机喷头动平台的位姿参数。通过消元法解方程组，最后求得动平台打印喷头的位姿参数。

(10)

其中，S1=N12+N42+1,S2=N1N2+N3N4-CN4-2l1，S3=N22+N32-2cN3-M1;

M1=l2-l12-c2，M2=l2-l22-c2

M3=l2-l32-c2

图5 3D打印机简化模型

图6 添加三组滑块驱动函数

4 运动学仿真分析

机构仿真模块是PRO/E软件的功能模块之一，可用于装配体的运动学仿真与分析，可记录运动件的轨迹。先将3D打印机模型简化，加入适当约束条件，在PRO/E中进行模拟仿真。在三组滑块与导轨间添加移动副约束，连杆与滑块、打印喷头间添加球面副进行约束。简化后的模型如图5，图6所示：

选定一个平面，即z坐标确定，z=-50mm，则x=50sin(t1),y=50cos(t1),由于PRO/E中数据是相对于起点时间某时某刻的各关节的角度值，故取x=50sin(180t/π),y=50cos(180t/π),其中t为时间，单位为s。在分析中，设定l=213mm,R-r=80mm,把所有数值代入公式(9)，则

(11)

PRO/E软件中应用程序可实现机构仿真功能，打印喷头的运动由三组滑块的上下运动决定。在PRO/E软件中，在三组滑块上添加三个伺服电动机，滑块运动方向为伺服电机的运动轴方向，通过对三个伺服电动机定义位置添加公式(11)中三组驱动函数。添加函数如下图7所示。

图7 滑块L1、L2、L3的驱动函数

打开机构分析，分别设置分析类型为位置和运动学，设置开始时间为0s，终止时间为10s，帧频为10。通过分析，得到动平台在三个方向上的位置、速度和加速度运动轨迹如图8所示。

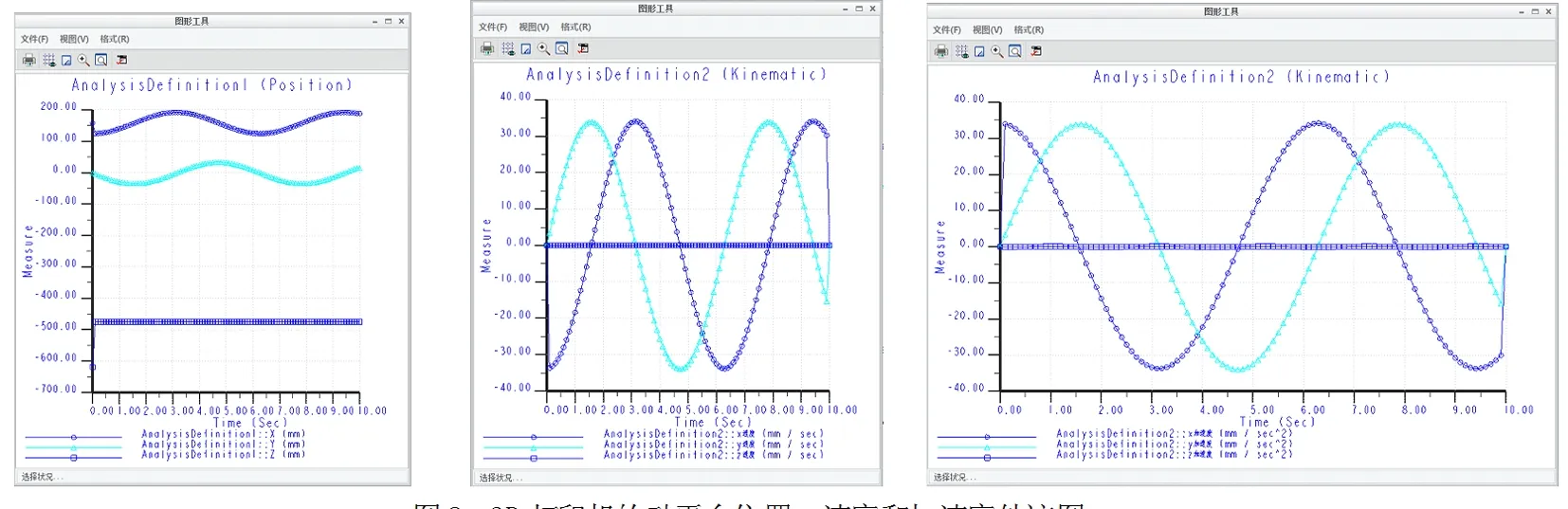
图8 3D打印机的动平台位置、速度和加速度轨迹图

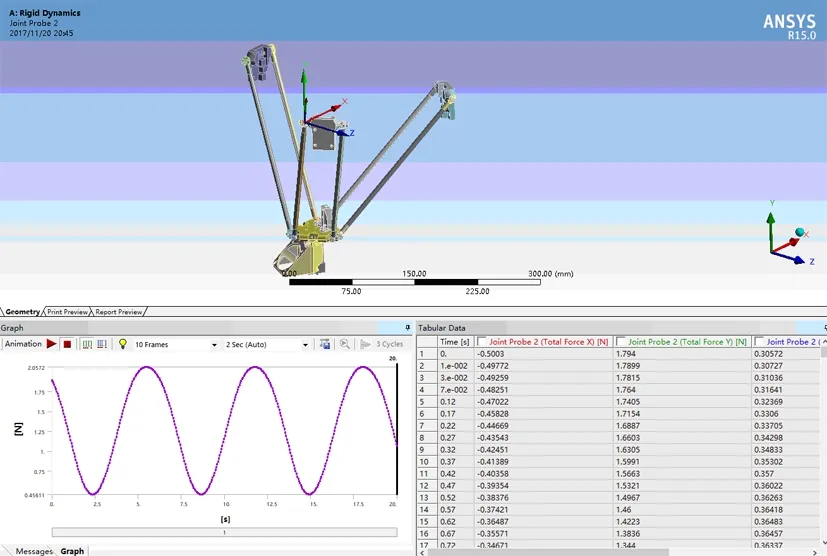
图9 虎克铰最大支反力

5 动态学仿真及虎克铰磨损分析

将3D模型导入有限元软件ANEYS Workbench的Rigid Dynamic分析模块中，对构件定义其密度属性并添加重力加速度。在三组滑块加上三组位置驱动函数，对打印机进行动态学仿真模拟，计算得到12个虎克铰处最大的支反力为2.057N。

该打印机中虎克铰自由转动，属于较高精度的间隙配合，其球径为Φ6(-0.01/-0.018)，球孔直径为Φ6(+0.012/0)。虎克铰在工作过程中自由转动，两球面接触面间在力的载荷作用下存在接触压力，球与凹球面间的接触应力计算公式如下：

上式中，F为虎克铰支反力；E为弹性模量；R1为球面半径；R2为凹球面半径

根据上式可以计算出该虎克铰应力圆上最大接触压力P。由公式可知，当R2最大，R1最小时，其接触压力最大。此时R2=3.006mm，R1=2.991mm.根据动态学仿真结果可知F=2.057N。该虎克铰使用了304不锈钢材料，其材料弹性模量E=2.1×105N/mm2=2.1×105MPa，代入公式(12)计算得到接触压力P=21.36 MPa。

打印机在工作过程中虎克铰的转动频繁，转动过程中接触面间面积较小，易磨损，可近似用线接触磨损模拟。根据文献[3]可得线磨损度表达公式如下：

(13)

其中，dh/ds表示线磨损度，即相对滑行ds的距离，在其垂直方向上磨损的厚度dh；K为磨损系数，与磨料和被磨材料的硬度、表面情况等相关；P为表面应力；H为材料的硬度。根据计算所得的P=21.36MPa，硬度查询材料标准可得H=210MPa，该虎克铰是钢-钢配合，根据文献[4]可知磨损系数K≈10-5,代入计算得到线磨损度dh/ds=1.017×10-6。

6 结 语

针对并联臂式3D打印机，对其结构和自由度进行了分析计算，得到该3D打印机是需要三个驱动的三自由度系统。并建立了打印机的空间坐标系，采用空间向量的有向性，运用数值分析法推导出了并联机床的正反解运动方程，为并联机构速度、加速度、误差分析等后续的研究提供了一定的理论依据。机构直接使用PRO/E软件中的机构分析模块，即可完成对三组并联臂和动平台打印喷头的位置和运动仿真分析，验证了运动学方程正反解的正确性，并说明了该机构具有良好的运动特性和运动平稳性。最后使用有限元分析软件对打印机进行dynalymic动态仿真模拟，求得虎克铰的最大支反力，并通过计算知虎克铰工作时的线磨损度很小，为预估该3D打印机的寿命提供了一定的理论依据。