箍筋下料长度计算方法对比分析①

,

(安徽建筑大学土木工程学院，安徽 合肥 230601)

0 引 言

目前，社会上存在多种箍筋下料长度的计算方法，但是各方法却不尽相同。其中，一些箍筋下料长度的计算方法是来自于日常的施工经验。虽然这类计算方法能够满足工程要求，但计算结果不够精确。认真分析各种箍筋下料长度计算方法，提出一种较为精确的计算方法。该方法有利于相关工程人员更为深刻地理解箍筋下料长度计算原理，同时亦更满足规范要求。

1 常见箍筋下料长度计算方法及分析

工程中对箍筋下料长度计算方法有多种，一般常见的有传统中心线长度计算法、以外包尺寸计算法和箍筋调整值法[1]。

1.1 传统中心线长度计算法

钢筋在弯曲加工过程中，钢筋外边线的长度会因拉伸作用而伸长，内边线长度因压缩作用而缩短，但中心线长度不会发生改变[1]。因此，利用该性质得出传统中心线为基准的箍筋下料长度计算方法[2]。按照图1所示，双肢箍筋下料长度计算公式如下：

不考虑抗震时:

L中=[(b-2c-d)+(h-2c-d)]×

2+2(l增+2d)

(1)

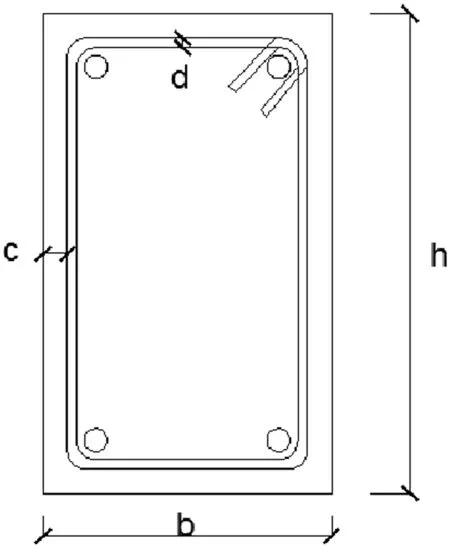
图1 双肢箍筋结构图

考虑抗震时:

L中=[(b-2c-d)+(h-2c-d)]×

2+2[l增+max(75-3d，7d)]

(2)

L中为箍筋传统中心线的下料长度；b为构件截面宽度；c为箍筋保护层厚度；d为箍筋直径；h为构件截面高度；l增为平直段长度为钢筋直径3d时的弯钩增加长度，一般90°弯钩取3.5d,135°弯钩取4.9d,180°弯钩取6.25d[2]。

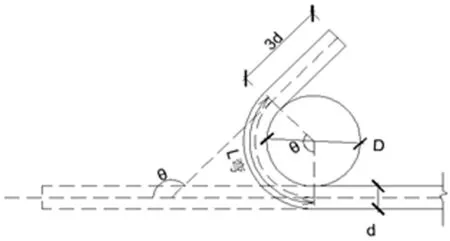
图2 非箍筋钢筋弯折结构示意图

根据现有规范要求，光圆钢筋弯弧内直径不应小于钢筋直径的2.5倍[3]，弯钩的弯折后平直段长度不应小于钢筋直径的3倍(见图2)；箍筋弯钩的弯弧内直径不仅要满足不应小于箍筋直径的2.5倍外，且不小于受力钢筋的直径[4]。对一般结构，箍筋的弯钩弯折角度不应小于90°，弯折后平直段长度不应小于箍筋直径的5倍；对有抗震要求的，箍筋的弯钩弯折角度应为135°，弯折后平直段长度不应小于max(75mm，10d)[5]。

1.2 外包尺寸计算法

如1.1中所述，钢筋弯曲加工过程中外边线伸长，因此在计算时需要通过减去相应的量度差值来调整。按图1所示，以钢筋外包尺寸为基准双肢箍筋下料长度计算公式如下[6][7]：

不考虑抗震时：

L外=[(b-2c)+(h-2c)]×2-3l量+

2(l增+2d)

(3)

考虑抗震时：

L外=[(b-2c)+(h-2c)]×2-3l量+

2[l增+max(75-3d，7d)]

(4)

L外—以外边线为基准箍筋的下料长度；

l量—钢筋弯曲量度差，即钢筋弯折后，弯弧部分外边线长度与中心线长度的差值，取值见表1；

表1 钢筋弯曲量度差取值(mm)

其他符号同上。

为了方便计算，钢筋量度差值弯弧部分外边线长度按切线长度和计算，因此也是近似计算。量度差值计算及取值如下[1][8]：

l量=(D+2d)tan(α/2)-(D+d)πα/360°

(0≤α≤90°)

(5)

l量=[(D+2d)tan(90°/2)-(D+d)π×90°/360°]+

[(D+2d)tan(β/2)-(D+d)πβ/360°]

(90°<α，β=α-90°)

(6)

D为钢筋弯折内径，取值按规范要求，光圆钢筋一般取2.5d[3]；α为钢筋弯曲角度。

1.3 箍筋调整值法

箍筋调整值是弯钩增加值和弯曲调整值两项代数和，因此，箍筋调整值法是一种简化的箍筋计算方法。这种计算方法一般通过计算箍筋的周长与箍筋调整值的和来确定箍筋的长度。根据上述方法并结合图1，双肢箍筋下料长度计算公式如下[2]：

量外包尺寸时：

(7)

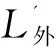
量内包尺寸时：

(8)

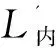
其他符号同前。

表2 箍筋调整值(mm)

2 中心线精确计算法

2.1 算法的提出

如前文所述，不难得出所有公式的基本原理都围绕着钢筋加工时外边线伸长，内边线缩短这个中心展开。但从公式推导看，显然都进行了近似计算。通过对上述方法的比较与分析，提出了一种新的算法—中心线精确计算法。该方法的基本思想是紧扣钢筋加工时中心线长度不变这个中心，通过几何分析准确找出箍筋的直段中心线长度和弯曲中心线长度，然后进行求和计算。这种算法下，箍筋下料长度计算公式表述如下:

L=L直+L弯+L端

(9)

L直为箍筋直线段中心线长度；L弯为箍筋弯曲段中心线长度；L端为箍筋弯钩端部平直段长度，取值按相关规定[5]。

按图3L直示意图并结合图1双肢箍筋结构图，箍筋的直段长度计算公式如下：

L直=[(b-2c-2d-D)+(h-2c-2d-D)]×2

(10)

式中符号同前。

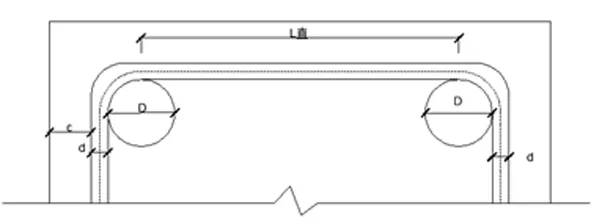
图3 钢筋直段长度示意图

按图3所示，并根据平面几何弧长公式可得箍筋中心线弯弧长度计算公式如下：

(11)

θ为表示钢筋中心线弯折角度对应的弧度；

其他符号同前。

综上可得，中心线精确计算法下双肢箍筋下料计算长度计算公式如下：

L=[(b-2c-2d-D)+(h-2c-2d-D)]×

(12)

θ1、θ2为分别表示箍筋中心线不同弯折角度对应的弧度；

其他符号同前。

2.2 比较分析

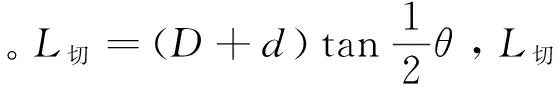
3 算法实例分析

前文从理论上分析并论证了传统中心线法、外包尺寸计算法、箍筋调整值法和中心线精确计算法，现就具体实例作对比分析。某混凝土梁，截面尺寸300mm×600mm，箍筋保护层取20mm，箍筋Φ10，考虑抗震，其截面如图5所示。

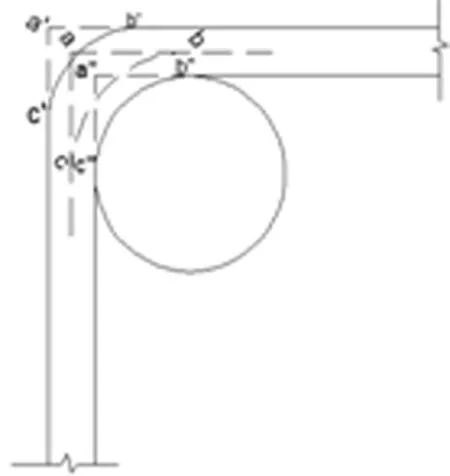
图4 (a)钢筋弯曲近似计算简图

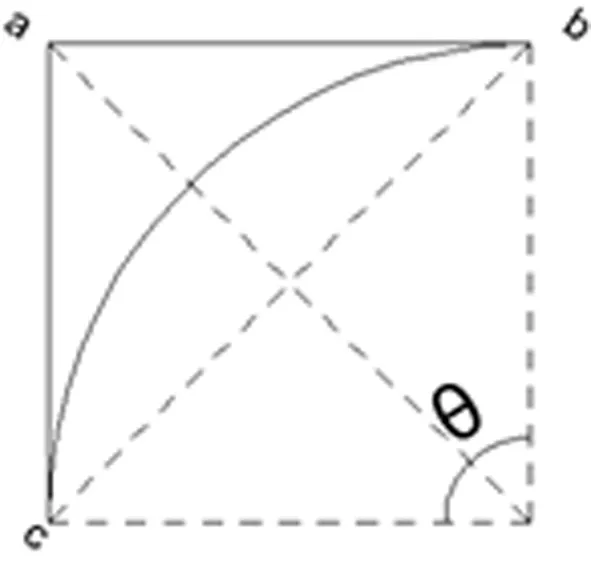
图4(b) 钢筋弯曲近似计算大样图

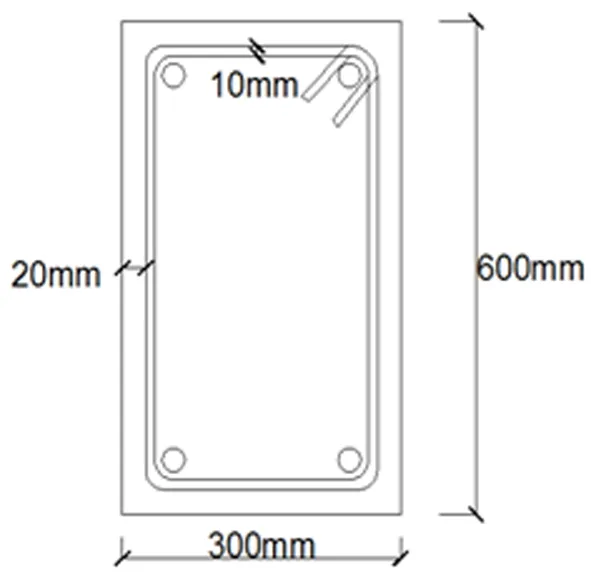
图5 双肢箍筋计算简图

传统中心线法：

L中=[(b-2c-d)+(h-2c-d)]×

2+2[l增+max(75-3d，7d)]=

[(300-2×20-10)+(600-2×20-10)]×

2+2×(4.9×10+7×10)=1838(mm)

外包尺寸法：

L外=[(b-2c)+(h-2c)]×2-3l量+

2[l增+max(75-3d，7d)]

=[(300-2×20)+(600-2×20)]×2-

3×1.75×10+2×(4.9×10+7×10) =1826(mm)

箍筋调整值法：

量外包尺寸时：

=[(300-2×20)+(600-2×20)]×

2+70=1710(mm)

量内包尺寸时：

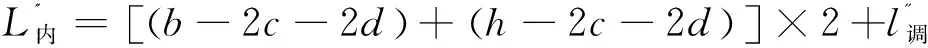
[(300-2×20-2×10)+(600-2×20-2×10)]× 2+150=1710(mm)

中心线精确计算法：

L=[(b-2c-2d-D)+(h-2c-2d-D)]×

2+2L端=[(300-2×20-2×10-2.5×10)+

(600-2×20-2×10-2.5×10)]×2+

(2.5×10+10)×2+2×10×10=1825(mm)

通过上面数据可以看出：双肢箍筋下料计算长度的中心线精确计算法要比传统中心线计算法和以外包尺寸计算法的数据要小。事实上，对于箍筋下料长度的精确计算的结果不一定就比其他计算方法的结果小，也有可能比其他计算结果大，但却是最能满足规范要求和符合钢筋下料实际。尽管箍筋调整值法所计算的箍筋下料长度比较小，但是表2中没有考虑抗震对平直段长度的要求。因此，箍筋调整值法是箍筋下料长度计算法中最不精确的算法，且与工程实际差距较大，一般不使用此计算方法。

4 结 论

通过从理论和实例两方面对传统中心线计算法、外包尺寸计算法、箍筋调整值法和中心线精确计算法四种箍筋下料长度计算方法进行对比分析，得出如下结论：

(1)中心线精确计算法有效可行，并且更符合规范和施工精度要求；

(2)虽然文中是以双肢箍筋为例对几种算法展开论证和分析并提出中心线精确计算法，但是这种算法的思想对单肢箍、多肢箍、多边形箍筋下料以及其他钢筋下料计算中都适用，其方法可供工程施工中借鉴应用。