利用数据融合改进超短基线系统定位精度

黄 健，严胜刚

(西北工业大学航海学院，陕西 西安 710072)

超短基线(ultra-short baseline，USBL)定位系统是一种常用的水下声学定位设备[1-4]。常规的USBL系统通过测量各通道间的相位差或时延差估算目标方位，再利用应答或同步方式测量目标的斜距，进而确定目标的位置。

USBL系统的设计是水下声学定位技术中的一项关键技术，平面阵可以对整个空间或以阵列所在平面为界的半空间中的目标进行定位，在许多情况下都可以达到系统的设计要求。文献[5—6]研究了平面阵的定位原理，并进行了详细的误差分析。文献[7—10]提出了平面八元阵定位原理，通过增加阵元个数有效地解决了USBL系统中存在的相位差模糊问题。文献[11—12]介绍了一种三维立体USBL系统接收阵列的设计。文献[13]在六元对称阵的基础上，给出了若干种USBL系统定位算法。由于基阵孔径小，且复杂的水下环境容易导致信号的相位产生起伏，常规USBL系统定位精度不高。为了满足远距离定位要求，必须对常规USBL系统进行改进。

本文在常用的平面阵定位原理及定位方程的基础上提出一种提高USBL系统定位精度的方法。以平面五元十字阵为例，系统仅需要测量一次时延差值，即可通过基本的平面阵独立地对目标进行定位，随后将这些独立的定位结果进行有效的数据融合，进而得到最终的定位结果。仿真试验表明,该方法可以有效地提高低信噪比情况下USBL系统的定位精度和可靠性。

1 USBL系统的基本原理

平面五元十字阵的定位原理如图1所示。在图1 中，平面五元十字阵由两条正交的线阵S1-S0-S3和S2-S0-S4构成。阵元间距为D，以基阵中心S0为坐标原点O建立直角坐标系，5个阵元的坐标分别为S0(0,0,0)、S1(D,0,0)、S2(0,D,0)、S3(-D,0,0)、S4(0,-D,0)。假设目标位于T处，T′为T在xoy平面上的投影。T的直角坐标为(x,y,z)，球坐标为(R,φ,θ)，R、φ、θ分别为目标到基阵中心的斜距、方位角和俯仰角。其中，斜距R=Δt·c，Δt为信号从目标到阵元S0的传播时间，c为声速。

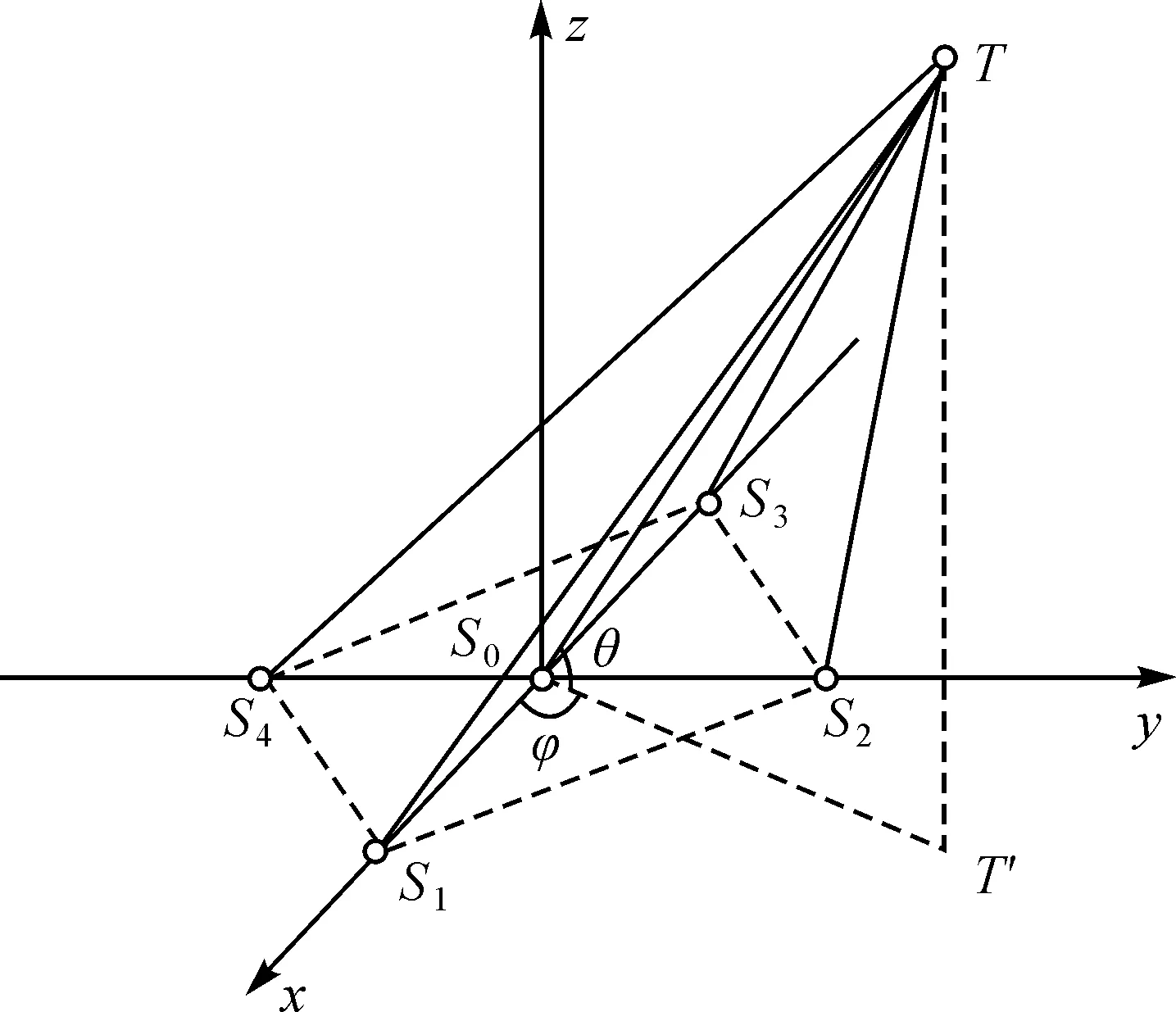
图1 平面五元十字阵定位原理

为了确定目标方位，USBL系统至少需要由3个基元构成[14]，令声信号由目标传播到阵元Si的时延为τi，且τij=τj-τi，则三元阵可以通过以下公式计算目标的方位[15]

(1)

十字正交阵与三元阵定位原理相同。图1所示的五元十字阵中包括8个正交的三元阵：USBL012、USBL023、USBL034、USBL041、USBL123、USBL234、USBL341、USBL412(下标的数字为所包含阵元的标识)，以及1个十字正交阵USBL1234。

在图1中，S1、S2、S3、S4这4个阵元构成平面四元十字阵，本文中标识为USBL4。平面四元十字阵的定位方程为[5]

(2)

平面五元十字阵(本文中标识为USBL5)是在平面四元十字阵的基础上在基阵中心增加了1个阵元S0，其定位方程为[6]

(3)

2 本文方法

在利用到达时延差(time difference of arrival，TDOA)测量值对目标进行定向的USBL系统中，系统定位精度与传感器和目标之间的相对几何位置关系有关[16]，不同的阵型对目标进行定位的精度也存在差别。为此，本文通过下面步骤来对各基本阵型的初始定位坐标进行数据融合，以达到提高USBL系统定位精度的目的。

(1) 计算每个定位坐标到其余坐标的欧氏距离之和为

(4)

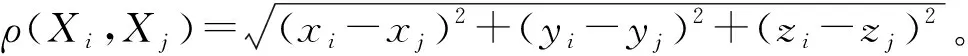
(2) 选择到其余点距离和最小的那个坐标点作为初始定位点的中心

(5)

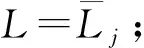
Lj>η·L

(6)

式中，η为经验参数。其值的大小决定着参与数据融合的有效点的个数。

(4) 对有效点的坐标运用LS(Least Square)方法，得到最终的定位结果。

3 仿真试验

(7)

通过式(8)来计算定位距离误差的平均值和标准差，并对比各系统的定位精度

(8)

式中，N=360，为测试的次数。

改变接收信号的信噪比，测试USBL系统在不同信噪比条件下的距离定位精度。接收信号信噪比范围设置为[-10 dB，20 dB]，目标与USBL系统之间的俯仰角取为θ=40°。测试结果如图2所示。

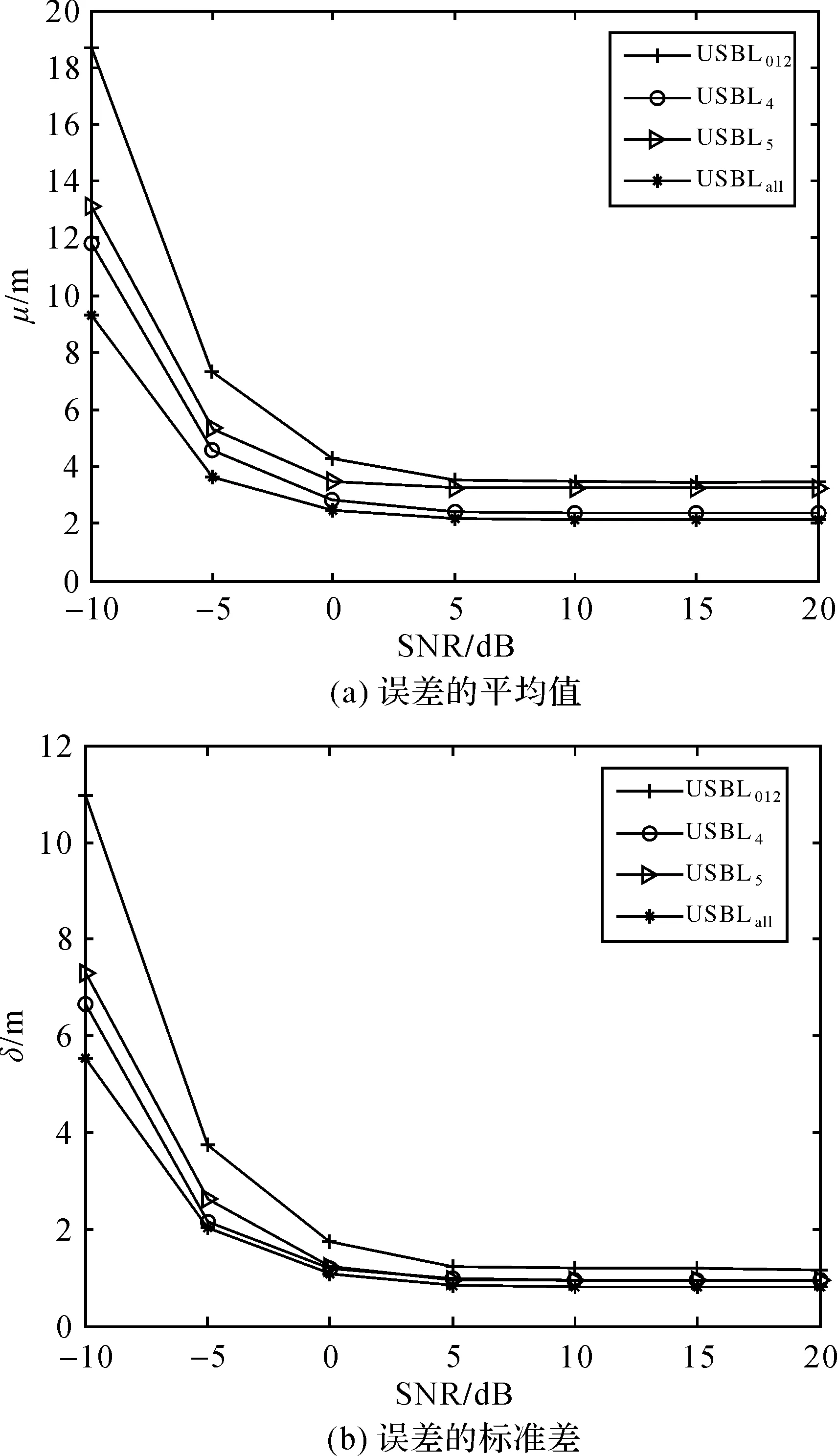
图2 各阵型USBL系统定位精度与信噪比的关系

从图2可以看出，在信噪比较高的情况下，各种基本阵型都具备较好的定位性能，但是在信噪比较低的情况下，各种基本阵型均容易出现较大的定位误差。本文方法综合了各基本阵型的定位结果，选择了其中较可靠的定位结果进行融合，使得系统总体的定位性能随着信噪比的降低而下降得更为缓慢。试验结果说明,本文方法可以有效地提高低信噪比情况下USBL系统定位的精度和可靠性。

通过测量USBL系统在给定俯仰角情况下的定位精度来测试各阵型定位方法与俯仰角之间的关系，信噪比固定为-5 dB。试验结果如图3所示。

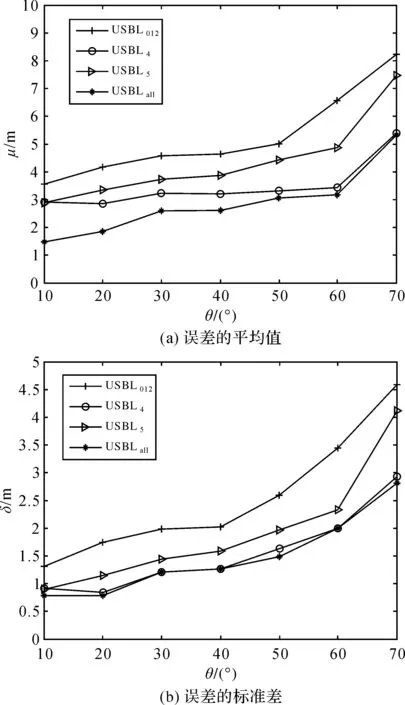
图3 各阵型USBL系统定位精度与俯仰角的关系

由图3可以看出，与另外3个阵型的USBL系统相比，USBLall系统在目标位于不同俯仰角的情况中，距离定位误差的平均值和标准差都相对较低，说明本文方法可以提高目标位于不同俯仰角情况下USBL系统的可靠性和精度。

使用本文方法对目标进行定位，通过改变经验参数η的取值来测试其对USBL系统定位精度的影响。试验中信噪比固定为-5 dB，目标与USBL系统之间的俯仰角θ=40°。通过以1°为步长改变目标方位角来改变目标的真实坐标，令第i次定位过程中有εi个初始定位点被判断为异常点。通过式(9)计算异常点的平均数

(9)

式中，N=360为测试的次数。同时，试验还通过式(7)和式(8)计算了不同经验参数情况下定位距离误差的平均值和标准差。试验结果如图4所示。

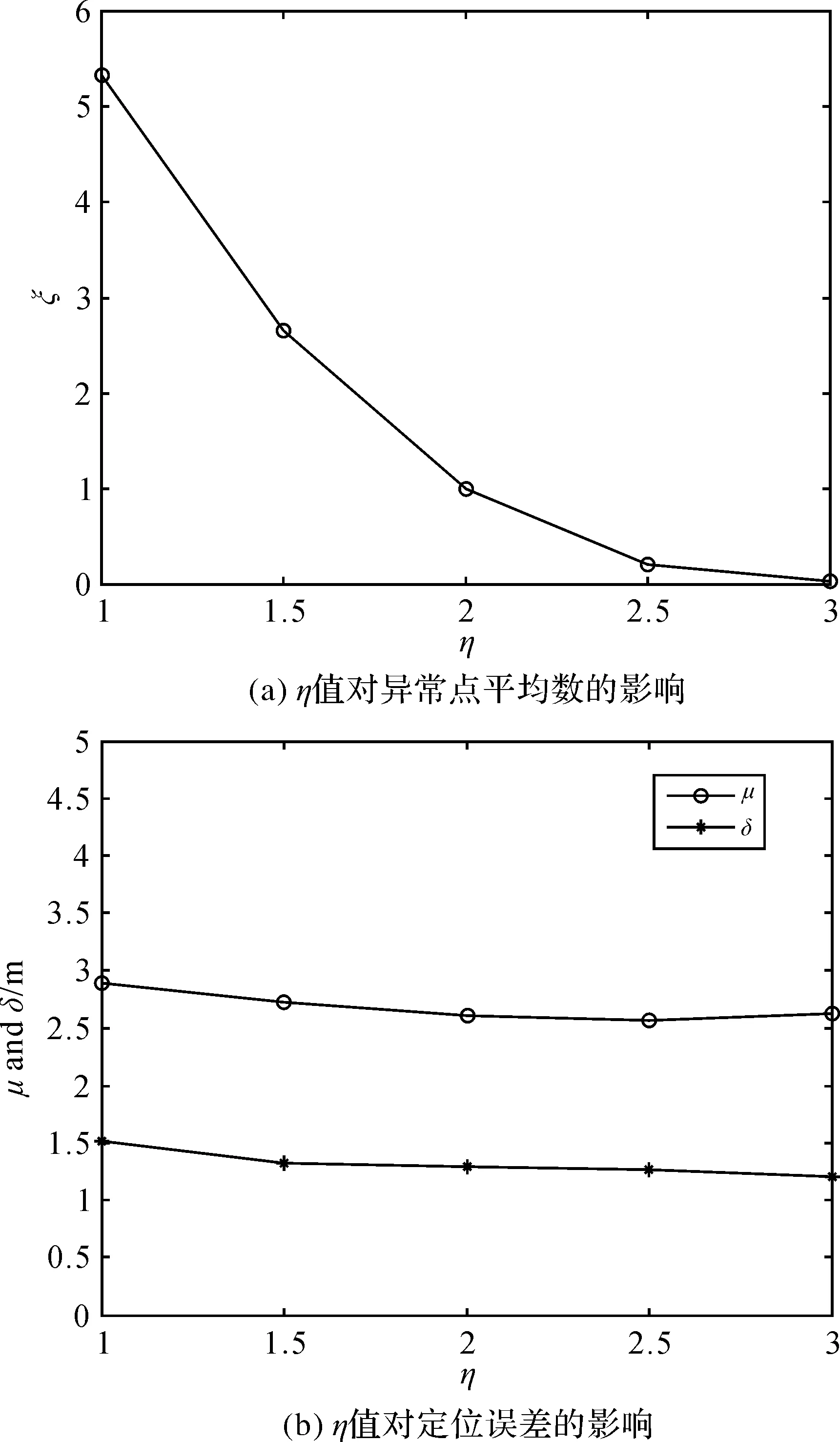
图4 η值对距离定位误差的影响

由图4可以看出，η的不同取值对基本阵型定位结果中被视为异常点的个数有较大影响，但是其对最终数据融合后的USBL系统定位结果影响不大。不同的η值所得到的距离定位误差，其平均值和标准差都保持相对稳定。

4 结 语

本文提出了一种利用数据融合改进USBL系统定位精度的方法。系统仅需要测量一次信号到达各阵元的时延，通过综合各种阵型定位结果，即可达到提高USBL系统可靠性和定位精度的目的。通过仿真试验证明了本文提出的方法在不同信噪比和目标处于不同俯仰角的情况下均能提高USBL系统的定位精度。