基于管理熵的景区游客时空分布优化仿真研究

胡明明 赵 容 戈 鹏 任佩瑜

(1.广西大学商学院,广西南宁 530004; 2.四川大学商学院,四川成都 610065)

0 引言

旅游业作为我国国民经济的战略性产业,具有资源消耗低,带动系数大,就业机会多,综合效益好等优势*中国网.国务院关于加快发展旅游业的意见 国发〔2009〕41号[EB/OL].(2009-12-04).http://www.china.com.cn/policy/txt/2009-12/04/content_19005236.htm.。但是,旅游业的快速发展在有效推动地区经济发展的同时,也给其生态环境、社会文化带来较大的负面影响(章小平 等,2009;黄萍,2007)。旅游资源的过度开发、景区的粗放式经营、环境质量的急剧恶化等严重威胁旅游业的可持续发展(戈鹏 等,2013)。

随着旅游业的迅猛发展,景区管理引起了国内外研究者的广泛关注(郑天翔 等,2015)。游客时空分布作为景区运营秩序的主要体现,已经成为一个研究热点。景区游客时空分布管理是消除安全隐患、提高游客满意度和扩大景区承载能力的重要手段,也是缓解旅游发展与保护生态环境之间矛盾的关键。20世纪90年代之前,游客运动通常被看做一个黑箱来解释旅游现象和游客行为,而不是作为一个被解释和探索的现象(Haldrup,2004)。在此之后研究者们意识到游客运动模式研究具有重要的理论和实践意义,因此开始进行一系列的实证研究。例如:Kemperma(2000)侧重于从时间维度来研究游客在主题公园的时空运动模式,通过对比初次游览游客和再次游览游客在主题公园内运动模式的差异,指出两种类型游客在选择活动的顺序上存在较大差异。Connelld等(2008)以苏格兰国家公园和罗蒙湖为例,基于社会网络模型分析了自驾车旅游的空间旅游流结构。Xia等(2011)研究了游客在菲利普岛自然公园(Phillip Island Nature Park)的时空运动模式。Orellana 等(2012)运用 GPS 技术收集了游客分布信息,探索游客在自然休闲区的运动模式。Smallwood 等(2012)研究了澳大利亚西北部大型海洋公园游客运动模式,他们收集了 1208 名游客的运动轨迹进行分析,结果表明游客的运动主要取决于道路网。Wolf 等(2013)利用GPS定位技术研究了采用不同导游媒体的游客轨迹,结果表明GPS导览系统显著优于传统媒体。Versichele等(2014)采用蓝牙追踪技术,对游客游览路径进行模式挖掘。Zoltan等(2014)通过分析当地管理机构出售的“目的地卡”的使用模式,调查了瑞士提契诺州的游客行为,结果表明游客运动表现出空间高度集中趋势,进一步明确了游客活动偏好。

国内景区游客时空分布相关研究起步较晚,且与国外景区及其游客游憩行为存在很大差异,研究的侧重点不同(黎巎,2013)。李君轶(2013)指出,利用旅游数字足迹研究游客行为是旅游业发展的应用方向,且主要集中在游客时空行为的数字足迹模型、游客旅游行为的时空规律、高效的旅游行为智慧化支持机制和旅游目的地空间结构优化研究等几个方面。黄潇婷(2009)通过时间、空间、活动和路径等指标将游客按时空行为模式划分为6种类型。李春明等(2013)提出了借助带有地理参考信息的照片研究游客时空行为的方法,并分析了游客在鼓浪屿景区的时间变化(日变化、周变化和月变化)、停留时间、日均游客量、游客流向图和旅游热点区域。黎巎(2013)针对景区旅游高峰期游客游憩质量下降、游憩安全和景区环境资源可持续利用等问题,建立了可动态模拟景区游客时空分布的游客游憩行为仿真模型。戈鹏等(2013)通过对九寨沟进行仿真,分析了旅游旺季景区内客流的时空变化特征,并提出了静态分流与基于区域时空负荷率的均衡动态分流相结合的策略。黄潇婷等(2014)进一步利用GPS技术与日志调查方法收集游客的时空运动信息,并分析游客时空行为。杨敏等(2015)利用入境游客在游中和游后发布的旅游信息挖掘游客时空信息,发现并总结了入境游客行为的时空规律,为旅游目的地管理和营销提供科学参考。Li等(2016)以鼓浪屿为例,利用空间句法分析发现游客偏好与路网结构高度相关,在此基础上,通过对旅游网站、旅游线路、历史街区的网络整合,提出了评价和引导旅游空间组织和历史遗产保护的相关建议。

通过梳理国内外文献发现,从研究的空间尺度来看,游客时空分布研究对象包含宏观尺度的目的地间(Inter-Destination)的游客时空分布和微观尺度的目的地内(Intra-Destination)的游客时空分布。游客行为特征在研究的尺度、精细度、重点等方面都有显著性差异。从研究方法来看,主要采用数理统计和计算机仿真,且采用数理统计方法的居多。由于涉及游客游憩行为的游客时空分布系统是一种复杂的动态系统(黎峻 等,2011),难以用传统的数量方程或回归统计进行线性分析。因此,数理分析的方法难以解决景区游客时空分布系统中普遍存在的非结构化问题和不确定性问题。鉴于计算机仿真方法能够在模拟实验和仿真阶段通过决策方案和分流效果对游客进行模拟和预测,已有研究者利用仿真建模方法对景区游客管理进行了初步研究(戈鹏 等,2013;黎巎,2013)。但是已有仿真研究过于抽象和理想化,忽略了众多现实因素(比如,各个景点重要度差异,不同交通方式差异,等等),没有真实地描述景区游客时空分布情况。这类仿真模型会导致对景区游客时空分布研究的效果不佳,难以指导景区游客管理。

本文基于管理熵理论,构建景区游客时空分布动态优化模型。通过对游客时空分布系统的可控参数进行控制,充分认识旅游客流在景区内的分布特征和移动规律,以实现有效的流量控制和分流调节,优化景区游客时空分布系统的管理熵值。本研究将有助于提升游客体验,实现自然风景区可持续发展。

1 相关理论和概念

1.1 管理熵理论

1997年,任佩瑜提出管理熵(Management Entropy,ME)与管理耗散结构(Management Dissipative Structure,MDS)理论。之后,任佩瑜等(2013)又系统地阐述了管理熵和管理效率递减规律、管理耗散结构和管理效率递增的规律。冯刚等(2010a)提出了采用时空分流导航技术、RFID和3S等技术为景区系统引入负熵,从而降低系统的管理熵值,提高景区游客管理效率。此外,冯刚等(2010b)还将管理熵函数应用于景区管理绩效评价。骆毓燕等(2011)在管理熵视角下,构建低碳化景区多维综合集成评价体系,从宏观和微观角度系统地揭示景区低碳化建设的状态及发展趋势。

(1) 管理熵

管理熵理论认为任何一种管理的组织、制度、政策、方法在相对封闭的组织运动过程中,都会呈现出有效能量逐渐减少、无效能量不断增加的一个不可逆的过程,从而导致组织结构中的管理熵增、管理效率递减(任佩瑜,1997)。管理熵的数学模型表达如下:

(1)

式(1)中,S表示管理熵,n表示影响管理熵变化的因素个数,i表示影响管理熵变化的各种因素的序数,ki表示系统在特定阶段第i种影响因素的权重,Si表示第i种影响因素所产生的熵值。

第i种影响因素所产生的熵值Si可以表示为:

(2)

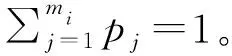
(2) 管理耗散结构

本文将景区游客时空分布系统看作一个相对封闭的系统,基于管理熵函数对景区游客时空分布进行定量分析,构建景区游客时空分布动态优化模型。

1.2 景区游客时空分布系统

《旅游景区质量等级的划分与评定》(GB/T 1775-2003)定义:景区系统是指以旅游及其相关活动为主要功能或主要功能之一的空间或地域所构成的系统,该系统具有参观游览、休闲度假、康乐健身等功能,具备相应旅游服务设施并提供相应旅游服务的独立管理区。本文所研究的景区游客时空分布系统是景区系统的一个子系统,是景区内旅游景点、游览线路、交通工具、游客等要素构成的相互作用、相互联系、为游客提供游览服务的整体。

2 景区游客时空分布动态优化模型构建

2.1 参数设置

假设景区游客时空分布系统由n个景点、n个景点之间的游览线路、交通工具、信息技术和游客所构成。根据n个景点的空间位置及游览线路,则可构建景区游客时空分布系统网络结构模型(见图1)。

图1 景区游客时空分布系统网络结构 注:v1,v2,…,vn代表景点;实线代表景点之间的游览线路。

为了构建景区游客时空分布系统动态优化的数学模型,景区游客时空分布系统参数涉及:

n为景点的个数;

V={v1,v2,…,vn}为景点的集合;

E={e12,e23,…,e(n-1)n}为任意两个景点之间连接的集合;

C={c1,c2,…,cn}为各景点的环境容量的集合;

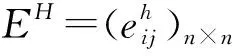
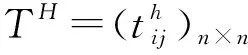
T={t1,t2,…,tn} 为各景点平均观光时间的集合;

W={w1,w2,…,wn}为景区内各景点重要性的集合;

A(t)={a1(t),a2(t),…,an(t)}为t时刻到达各景点的游客人数的集合;

D(t)={d1(t),d2(t),…,dn(t)}为t时刻离开各景点的游客人数的集合;

X(t)={x1(t),x2(t),…,xn(t)}为各景点t时刻的游客人数集合,即景区游客时空分布。

2.2 模型构建

游客时空分布是景区运营秩序的主要体现。景区游客时空分布系统内的可控参数主要是分流比率。分流比率指景区内游客的分流方案,决定了某时刻游客在景区内的流向,对景区游客时空分布具有关键作用。

系统分流比率动态优化是指在系统运行过程中的t0时刻,对系统的分流比率进行调整来达到对系统游客时空分布的最大熵进行控制的目的。假设景区开放时间为上午6∶00至下午6∶00,转换成分钟数,将游客游览时间区间设为t∈[0,720]。因此,分流比率优化模型的目标函数是:

(3)

游客时空分布系统管理熵的公式如下:

ME[x1(t),x2(t),…,xn(t)]=

(4)

式(3)和式(4)中,各景点t时刻的游客人数xi(t)可通过各景点t时刻到达的游客人数ai(t)来计算,即:

(5)

(6)

各景点分别通过栈道、公路、索道去往其他各景点的分流比率之和为1,即:

(7)

基于以上分析,本文构建游客时空分布系统t0时刻分流比率优化模型如下:

3 基于Simulink仿真的案例分析

3.1 景区游客时空分布系统Simulink仿真

基于计算机仿真建模的旅游模拟,有助于了解旅游者在景区的时空动态特点,探寻景区环境承载力,也有助于认识不同游客管理方案所产生的效果。以一个包含入口、出口和4个景点的景区为例,构建景区游客时空分布系统(见图2),并对其进行Simulink仿真。

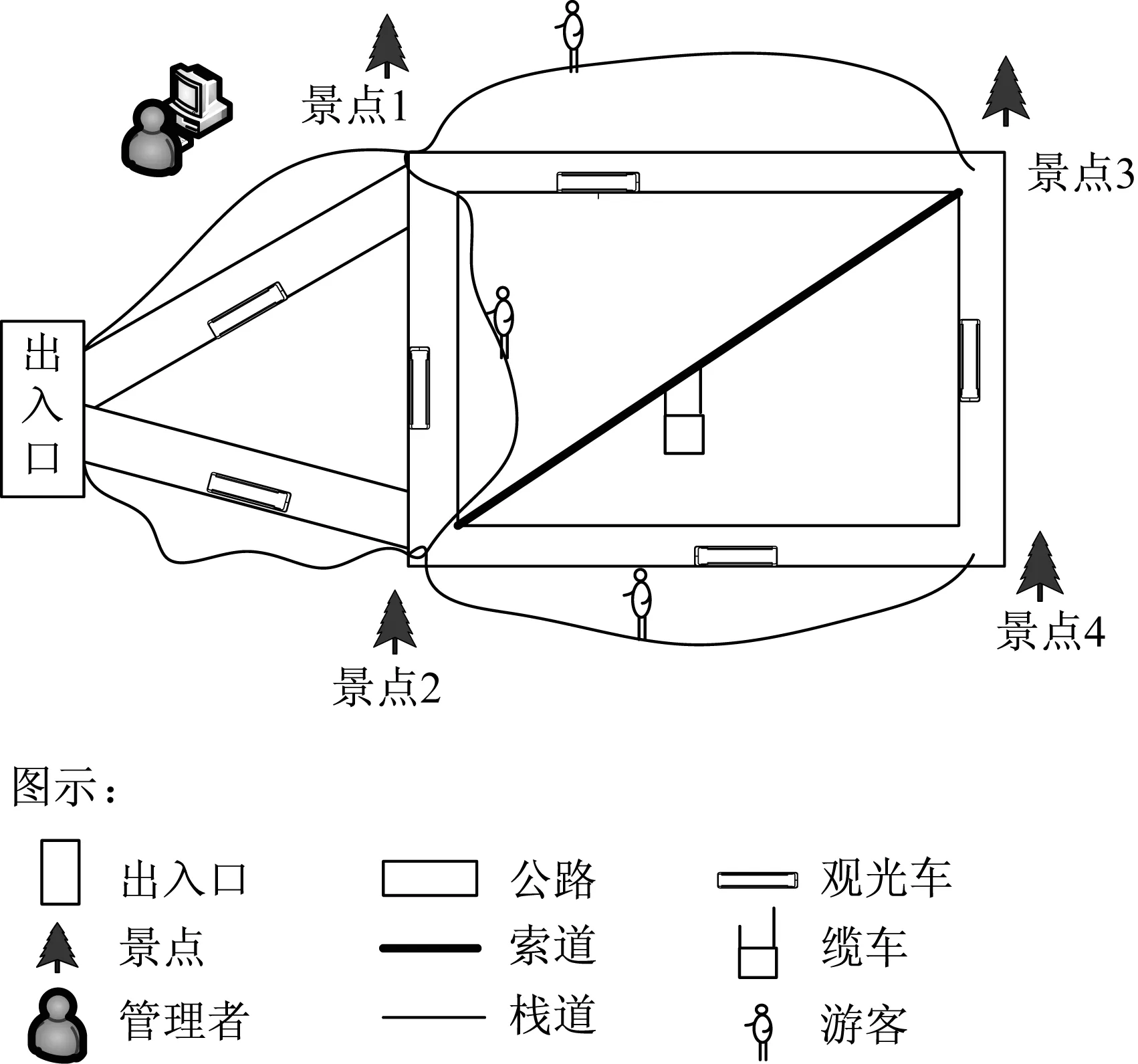
图2 景区游客时空分布系统示例

系统的输入参数如下:(1) 各时刻进入系统的游客人数;(2) 各景点之间以及景点与出入口之间的游客分流比率;(3) 游客在各景点花费的平均观光时间;(4) 游客分别通过栈道、公路、索道从一个景点到达另一个景点所花费的时间。

系统的输出参数如下:(1) 各时刻到达出口的游客人数;(2) 各时刻各景点的游客人数。

对系统输入参数进行模拟与设定:(1) 第t0分钟景区游客为1000人;(2) 游客分别通过栈道、公路、索道从一个景点到达另一个景点所花费的时间如表1所示;(3) 优化前,景点1、景点2、景点3、景点4、出口、入口之间分别进入栈道、公路和索道的游客分流比率如表2所示;(4) 游客时空分布系统内景点1、景点2、景点3和景点4的平均观光时间分别为15分钟、25分钟、30分钟、40分钟。

表1 景点之间栈道、公路、索道的时间距离(单位:分钟)

表2 进入栈道、公路、索道游客优化前分流比率

3.2 景区游客时空分布优化对比分析

以图2中的游客时空分布系统为例,Simulink仿真系统输出的各景点各时刻的游客人数如图3所示,时空分布系统内各景点游客负荷率随时间的变化如图4所示,游客时空分布系统管理熵随时间的变化如图5所示。

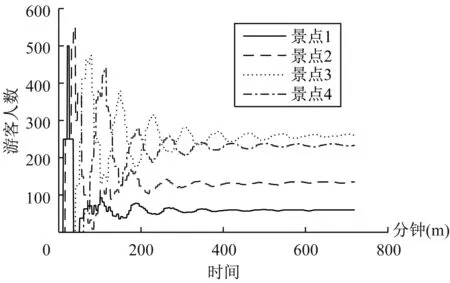
图3 参数优化前各景点游客人数随时间变化图

图4 参数优化前景点游客负荷率随时间变化图

图5 参数优化前游客时空分布系统管理熵随时间变化图

若采用表1中的游客时空分布系统t0时刻的分流比率为初始分流比率,在系统运行至t=t0+20分钟时对系统分流比率进行优化。将系统前t0+20分钟到达各景点的游客数据以及第二部分设定的其他参数输入模型,见公式(8),并采用Matlab优化工具箱内的遗传算法求解,可得到优化后的游客时空分布系统分流参数如表3所示。将优化后的分流比率参数与第二部分设定的其他参数一同输入Simulink仿真模型中,Simulink仿真系统输出的各景点各时刻的游客人数如图6所示,时空分布系统内各景点游客负荷率随时间的变化如图7所示,游客时空分布系统管理熵随时间的变化如图8所示。

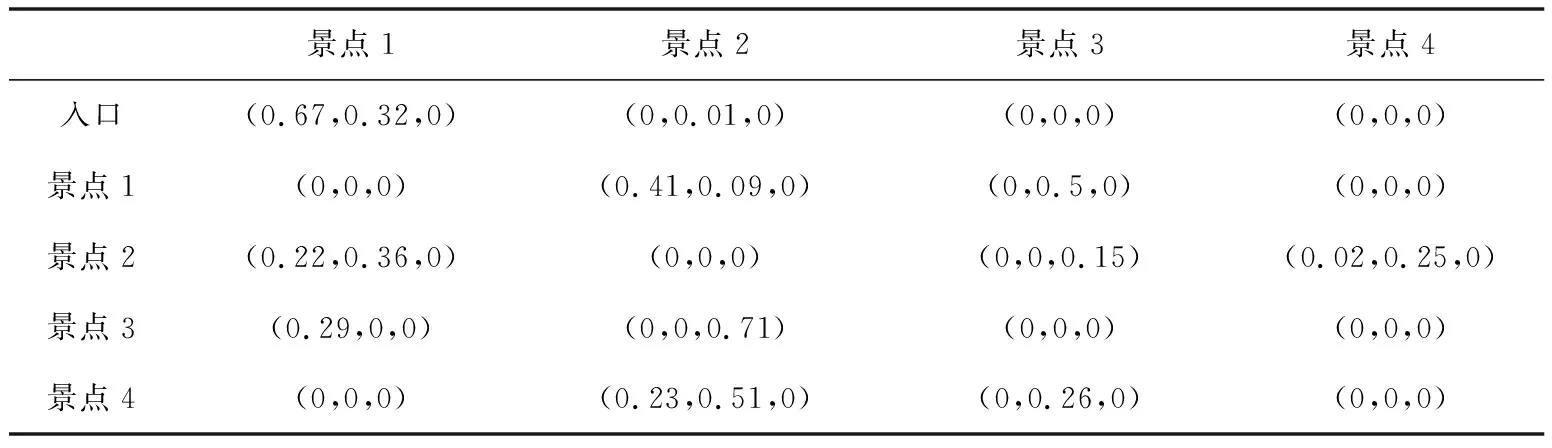
表3 进入栈道、公路、索道游客优化后分流比率参数

图6 动态优化参数后各景点游客人数随时间变化图

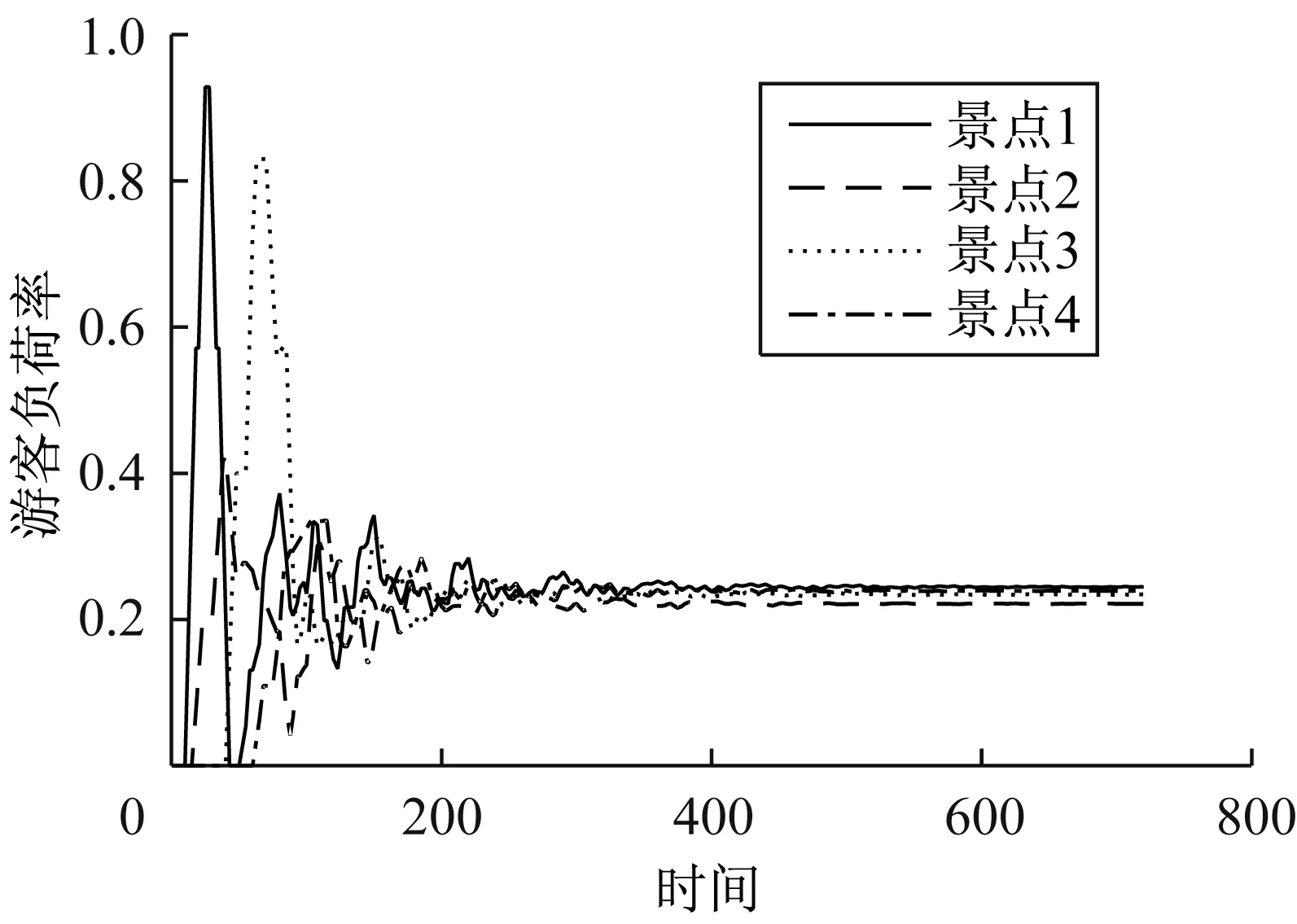
图7 动态优化参数后景点游客负荷率随时间变化图

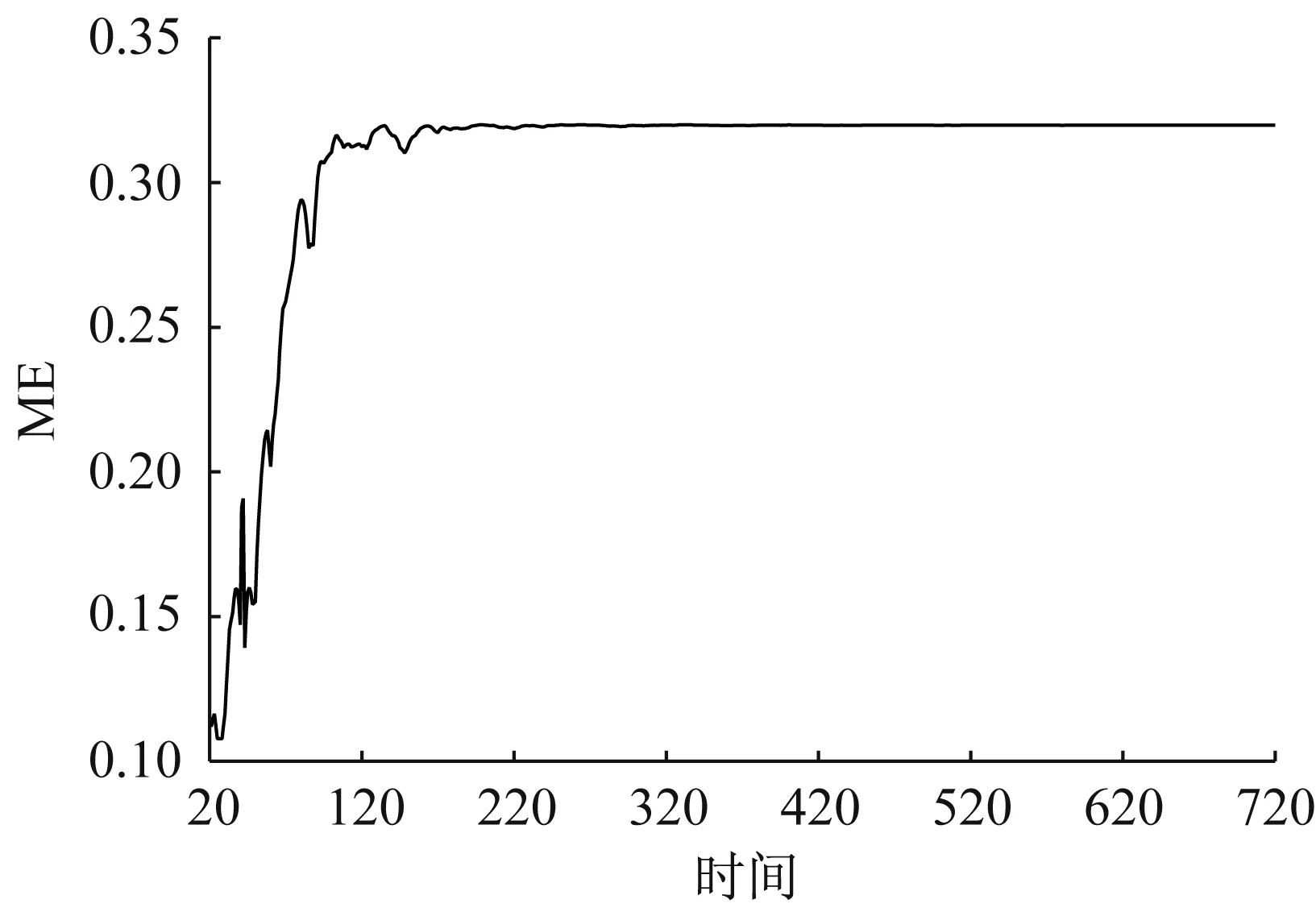
图8 动态优化参数后游客时空分布系统管理熵随时间变化图

通过参数优化前游客时空分布系统管理熵随时间的变化(图5)与动态参数优化后游客时空分布系统管理熵随时间的变化(图8)对比可以看出,参数优化前,游客时空分布系统管理熵的波动较大,最后稳定于0.16,处于不均衡状态。然而,参数优化后,游客时空分布系统管理熵稳定后几乎趋于0.32,达到游客时空分布系统管理熵的最大值,并且波动较小,收敛速度快。

同时,通过参数优化前的景点游客负荷率随时间的变化(图4)与参数优化后的景点游客负荷率随时间的变化(图7)对比可以看出,参数优化前,游客时空分布系统稳定后各景点的游客负荷率差别很大,景点3的游客负荷率高达0.8,而景点2的游客负荷率最小,不足0.1,系统处于极度不均衡状态。然而,参数优化后,在全系统的运行过程中,各景点游客迅速达到稳定状态。系统稳定后,游客时空分布系统各景点的负荷率几乎趋于一致,系统处于动态均衡状态。

通过以上对比分析,可以看出,景区游客时空分布优化模型对游客时空分布系统动态分流比率的优化效果明显,可以有效、实时地保持系统处于均衡状态,有效缓解景区游客局部拥堵,均衡游客时空分布,是同步实现景区环境保护和提升游客满意度的有效途径。

4 结论与管理建议

4.1 结论

游客规模过大造成的景区负荷过载可分为结构性过载和功能性过载。其中,结构性过载是景区全时空范围内负荷总量超过景区资源承载能力,源自景区承载能力的结构性不足,在不扩大景区规模的情况下,结构性过载必须通过限制旅游规模、倡导理性旅游才能彻底解决。功能性过载则源自景区的结构性矛盾,是游客人数未达到景区真实容量,但由于缺乏对游客过分集中现象进行科学管控,导致某些景点区域瞬时负荷过大,造成局部拥堵,对这些区域的生态环境造成不可恢复的破坏,同时极大地降低游客满意度。本文基于管理熵理论构建景区游客时空分布动态优化模型,通过Simulink仿真对景区游客时空分布系统进行案例分析,并采用遗传算法求解模型,主要解决景区负荷功能性过载的问题。对比仿真优化前后各景点游客人数时空分布、各景点负荷率以及景区时空分布系统管理熵值随时间变化的结果发现,该优化模型通过对游客时空分布系统的分流比率参数进行控制,能有效缓解景区游客局部拥堵,均衡游客时空分布,有助于同步实现景区环境保护、游客满意度提升。

进一步,研究结果表明,时空分流是解决景区拥堵和时空分布不均衡的关键。概括而言,采用景区游客时空分布优化模型或算法可以实现的效果包括:第一,景点的空间均衡,即在同一时刻整个景区内各个景点的负荷率均衡;第二,景点的时间均衡,即在不同时刻同一景点的利用率趋于稳定。本文以建模仿真的视角,综合考虑游客规模、多种交通模式(公路、栈道、索道等)、景点重要性、景点环境容量和景点平均观光时间等因素,建模仿真过程相较于前人的研究更进一步还原景区游客时空分布真实场景,能更好地指导景区游客分流调度,促进游客在景区内时空分布均衡。

4.2 管理建议

景区管理者在时空分流思想的指导下,需要结合上述诸多因素,针对不同游客规模以及不同景区游客分布情况,利用景区游客时空分布优化模型,制定科学合理的分流方案,并且根据游客时空分布变化,实时调整分流方案具体建议如下:

首先,理性控制游客规模。引导游客分时段进入景区,避免游客在景区入口过度集中;游客分时段进入景区可有效避免游客在景区入口排队等候,同时有效预防景区客流量发生瞬时井喷现象。

其次,多种旅游交通模式具有不同的特征(见表4),各种旅游交通模式相互交错,使景区时空网络呈现出多层性、多级性、多维性、多准则性、拥塞性、全局优化和个体优化协调性等特征。并且,在不同时段和不同游客规模下,游客的游览行为使得景区游线结构涌现出随时间演化的复合网络拓扑结构。在景区游客时空分布系统中表现为不同旅游交通方式的分流比率差异。景区管理者需要充分考虑景区不同交通模式的优缺点,通过栈道、公路、索道等多种交通方式控制关联景点客流传播速率,调整客流波形相位在时间上的延滞,避免游客负荷峰值在目标景点的同步叠加,实现游客负荷“削峰填谷”的效果。然后,根据景区时空分布优化模型给出的实时最佳分流方案,引导具有不同偏好的游客选择最适合自己的交通方式,同时分散客流,满足景区游客均衡分布需求。

表4 不同旅游交通方式特征

再次,国内很多景区在旅游高峰期都存在热门景点客流量大、拥挤度高、负荷率高,而部分冷门景点客流量小、负荷率低的不均衡现象,在动态优化模型中表现为景点的权重不同。一方面,景区管理者在设计空间分流方案时,一定要结合各个景点的重要程度合理进行区域分流,把游客分流到景区内各个景点,必要时可进行局部容量控制。另一方面,加大冷门景点宣传力度,进一步开发冷门景点,并且改善冷门景点的服务质量,在一定程度上提升冷门景点的吸引力,微调景区游客时空分布系统景点权重,潜移默化地引导游客在景区系统的分布状态。

此外,合理诱导游客调整景点观光时间。景点游客观光时间作为景区游客时空分布仿真模型的一个重要因素,间接影响游客在景区时空网络中的流通速度。当游客在一个景点的观光时间缩短,会加速客流向下游景点转移,增加下游景点的游客量。一方面,能够加速游客在整个网络的流通速度;另一方面,也存在将拥堵态势传递到下游景点的风险。当游客在一个景点的观光时间延长,会抑制游客在景区路网上的转移,甚至发生该景点游客量瞬时井喷现象。但是,当该景点游客量小,同时其下游景点游客过多时,诱导游客延长在该景点的观光时间,可以有效预防下游景点的游客拥挤现象。因此,合理调整景区游客时空分布仿真模型中的景点游客平均逗留时间,促进游客负荷波形在目标景点处出现“峰谷相合,峰峰相错”,有效避免游客在目标景点上的过分集聚。

总之,景区内景点游客负荷的累积受到关联景点上客流的分流概率、 游客波的传播速率、相位等因素的综合影响,景区管理者需要立足于空间的相对静态性和时间的动态性,对景区客流进行全时空范围内的动态优化,降低游客时空分布系统管理熵值,减小系统管理熵值的波动幅度,提升景区全时空范围内的序度,促进景区可持续发展。

5 研究不足与展望

本文基于管理熵理论,构建景区游客时空分布动态优化模型,进行景区游客时空分布动态均衡研究,对景区游客管理具有一定的指导意义,但还存在一定的局限性:首先,本文将景区游客时空分布系统抽象为仿真模型,将景区现实情境进行了简化抽象,在一定程度上对景区游客分布描述存在失真现象;其次,本文对景区游客时空分布系统的管理熵测度是在景点数目较少的情况下进行的,对景点数目众多的复杂系统的适应性还有待研究;最后,本文还未实现分流比率参数与景区观光车调度的融合,提出的景区时空分流方案指导景区观光车调度的效果有待进一步验证。

进一步探索景区时空分布优化潜能和效用,后续研究将重点突破以下方面:

(1) 在建模仿真过程中考虑更多现实因素,如季节、天气、节假日等,使仿真模型更真实地描述景区游客时空分布情况,并且更有效地指导景区游客管理。

(2) 将景区游客时空分布系统管理熵测度模型推广到景点数目众多的大型景区,加强该模型的适用性。

(3) 在景区观光车调度过程中,以景区时空分流方案作为观光车调度决策依据,依据时空分流比率优化结果提出景区观光车调度措施。