Gravity and Spin Forces in Gravitational Quantum Field Theory∗

Yue-Liang Wu(吴岳良)and Rui Zhang(张睿)

1Key Laboratory of Theoretical Physics,Institute of Theoretical Physics,Chinese Academy of Sciences,Beijing 100190,China

2School of Physical Sciences,University of Chinese Academy of Sciences,No.19A Yuquan Road,Beijing 100049,China

3International Center for Theoretical Physics Asia-Pacific(ICTP-AP),University of Chinese Academy of Sciences,Beijing 100049,China

AbstractIn the new framework of gravitational quantum field theory(GQFT)with spin and scaling gauge invariance developed in Phys.Rev.D 93(2016)024012-1,we make a perturbative expansion for the full action in a background field which accounts for the early inflationary universe.We decompose the bicovariant vector fields of gravifield and spin gauge field with Lorentz and spin symmetries SO(1,3)and SP(1,3)in biframe spacetime into SO(3)representations for deriving the propagators of the basic quantum fields and extract their interaction terms.The leading order Feynman rules are presented.A tree-level 2 to 2 scattering amplitude of the Dirac fermions,through a gravifield and a spin gauge if eld,is calculated and compared to the Born approximation of the potential.It is shown that the Newton’s gravitational law in the early universe is modified due to the background field.The spin dependence of the gravitational potential is demonstrated.

Key words:gravifield,spin gauge field,background field,quantum gravity,tensor projection operators,scattering amplitudes,modified Newton’s law

1 Introduction

The gravitational quantum field theory(GQFT)with spin and scaling gauge invariance was developed in Refs.[1–2]to overcome the long term obstacle between the general theory of relativity(GR)and quantum mechanics.In fact,there has been enormous efforts on the theory beyond Einstein’s theory since the GR was established by Einstein in 1915.[3]The metric describing the geometry of the spacetime are commonly factorized linearly to explore the quantum structure of gravity and its interaction with matter fields,[4−5]and the Ricci scalar has been shown to be the key of the dynamics of gravity.The property of GR with spin and torsion was investigated in Refs.[6–8]where the totally antisymmetric coupling of the torsion to spin was presented.The general quadratic terms of the 2-rank tensor fields that satisfy the ghost-free and locality conditions were discussed in Ref.[9].With the tool named tensor projection operators developed in Ref.[10],which projects the SO(1,3)tensor representation to the components of different SO(3)representations,the general propagators and gauge freedoms were investigated and extrapolated to a more general case including propagating torsion.[11]The totally antisymmetric part and its renormalizability was anayzed in Ref.[12].

Recently,a new framework of gravitational quantum field theory(GQFT)was proposed to treat the gravitational interaction on the same footing as electroweak and strong interactions,[1−2]where a biframe spacetime is initiated,namely,the locally flat non-coordinate spacetime and the globally flat Minkowski spacetime,a basic gravifield is defined on the biframe spacetime as a bicovariant vector field which is in general a 16-component field.The spin gauge field and scaling gauge field are introduced to keep the action invariant under a local SP(1,3)×SG(1)gauge transformation.A non-constant background solution has been obtained,which may account for the inflationary behaviour of the early universe.In a proceeding work,a more general action for a hyperunified field theory(HUFT)under the hyper-spin gauge and scaling gauge symmetries was proposed[13]to merge all elementary particles into a single hyper-spinor field and unify all basic forces into a fundamental interaction governed by a hyperspin gauge symmetry.A background solution remains to exist.In such an HUFT,it enables us to demonstrate the gravitational origin of gauge symmetry as the hypergravifield plays an essential role as a Goldstone-like field.The gauge-gravity and gravity-geometry correspondences lead to the gravitational gauge-geometry duality.It has been shown that a general conformal scaling gauge symmetry in HUFT results in a general condition of coupling constants,which eliminates the higher derivative terms due to the quadratic Riemann and Ricci tensors,so that the HUFT will get rid of the so-called unitarity problem caused by the higher order gravitational interactions.To demonstrate explicitly,in the present paper,we consider the gravitational interactions of gravifield and spin gauge field only in four dimensional case with a background field solution.Expanding the full action under such a background field,it is natural to extract the dynamics and interactions of the quantum fields.The interactions among these fields will reflect the gravitational behavior in the early universe.

2 Action Expansion in a Non-Constant Background Field

Let us start from a basic action by simply taking four dimentional spacetime,i.e.,D=4,from the hyperunified field theory(HUFT)[13]in hyper-spacetime,

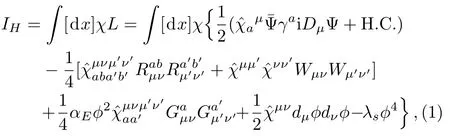
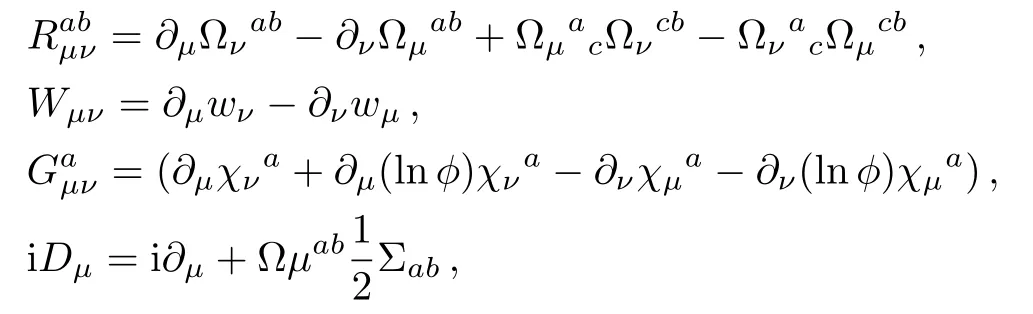
The tensors are taken the general forms presented in Ref.[13]

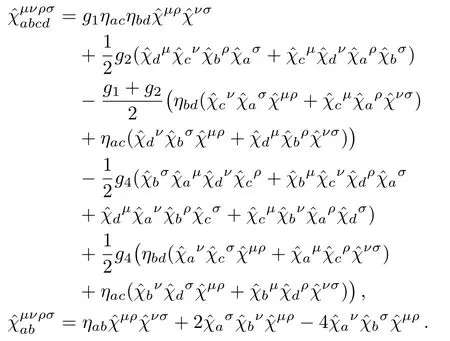
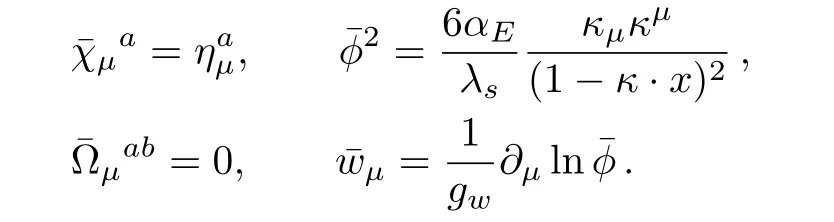
The quantized field are expressed as:

We can expand the action(1)and collect the leading order interactions and quadratic terms.As the quadratic term of the quantum gravifield includes a non-constant coefficientit is useful to absorb it into the field via a field-rede finition

The final quadratic terms are given by:

There are other terms,which involves two quantum fields,but with higher orders of the background field,we present them in the Appendix A.In the early universe,the background field ϕ(x)is sufficiently small,so that we can ignore the effect of those terms and only consider the quadratic terms in Eq.(2).

Though the propagators can hardly be read from the action,we can utilize the tensor projection operators to decompose the spin components of the tensor fields,and then derive their propagators.The scaling gauge field decouples from the Dirac spinors,so we would not include it in our present considerations.We shall discuss the details in Sec.3.We can also get the leading-order interaction terms,which are given in the appendix B.Notice that we have absorbed the gauge coupling constant gh,which depends on the normalization of coefficients g1,g2and g4.We shall do a field rede finition after some normalization of the propagator in Sec.5 and turn the interactions to a usual form of gauge interactions.

3 Tensor Projection Operators and Propagators of Gravifield and Spin Gauge Field as Well as Scalar Field

The SO(1,3)tensor-like fields hµaand Ωµabcan be decomposed into different SO(3)spin-parity components:Following Ref.[9],we shall de fine the tensor projection operatorswhere the subscripts f1and f2denoting the field type,the superscripts J and P label the spin and parity.The tensor projection operators satisfy the following relations:

with the de finition

To be specific,we write down the explicit forms for the tensor projection operator of the 2+component of the gravifield

with the de finition

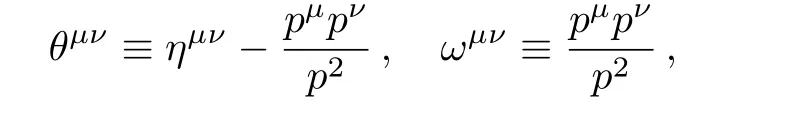
and the tensor projection operator of the totally antisymmetric part of the spin gauge field Ωµab,

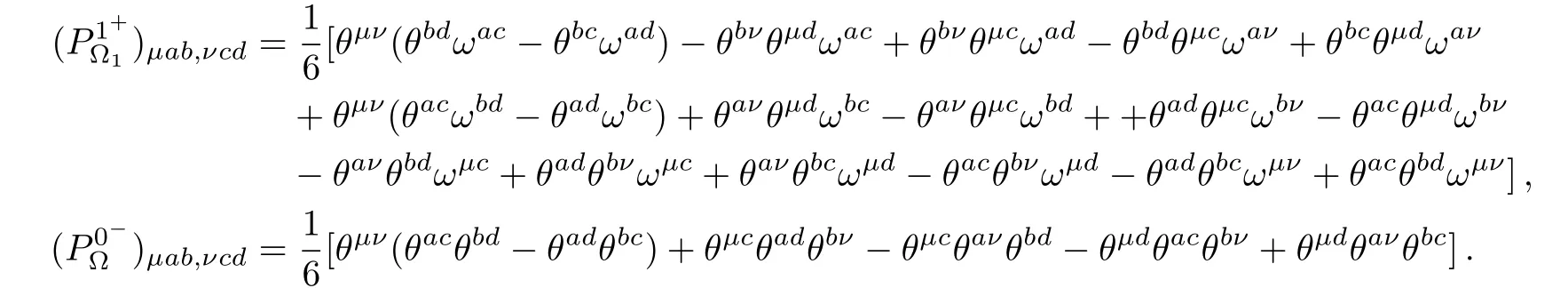
The explicit forms of other tensor projection operators are presented in the appendix C.

In general,the tensor projection operators have the following properties,

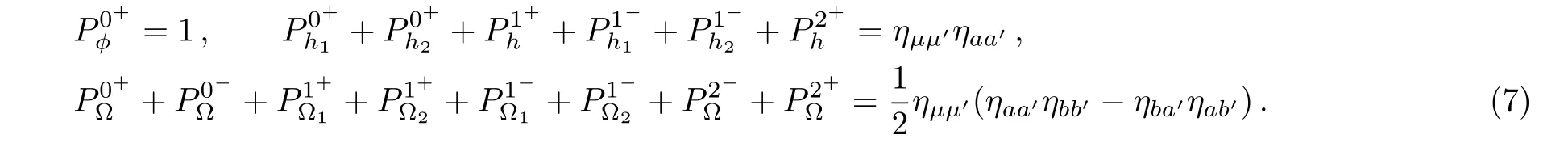
Thus we can write the quadratic terms of the action in terms of the tensor projection operators as follows,

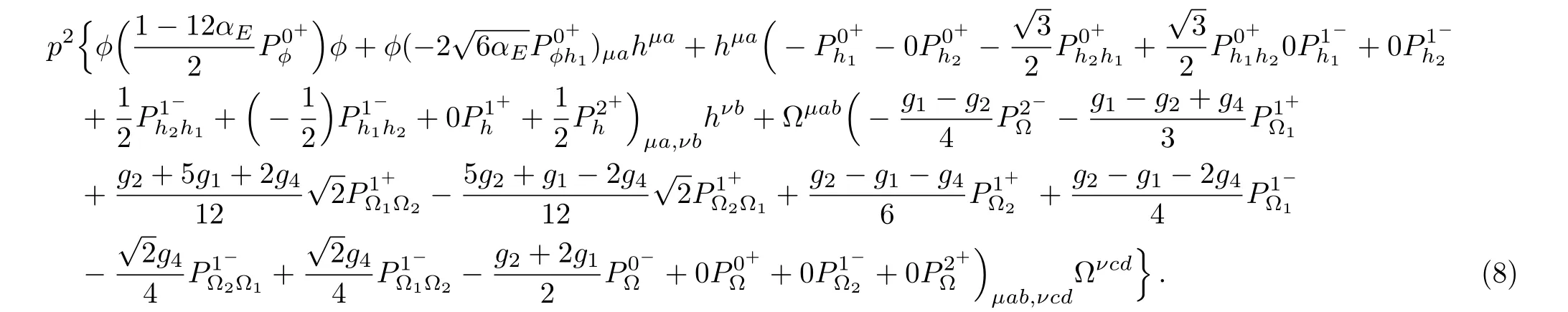
The field equations of the field typecan be expressed by tensor projection operators as:

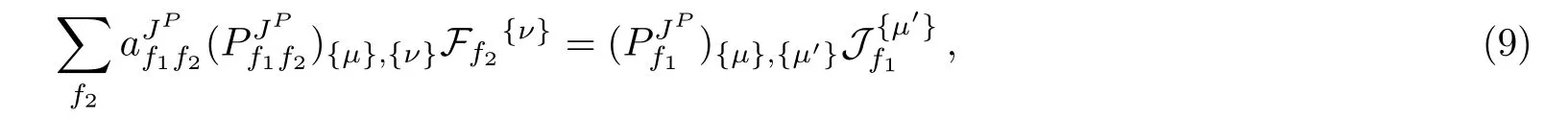
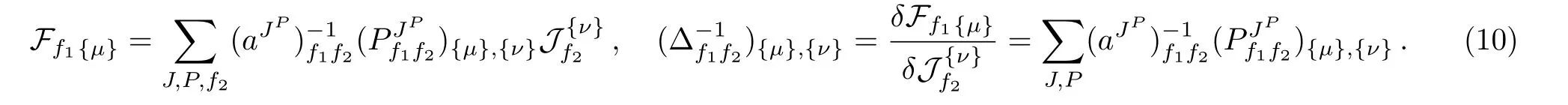
The explicit forms of the coefficient matrices are given by

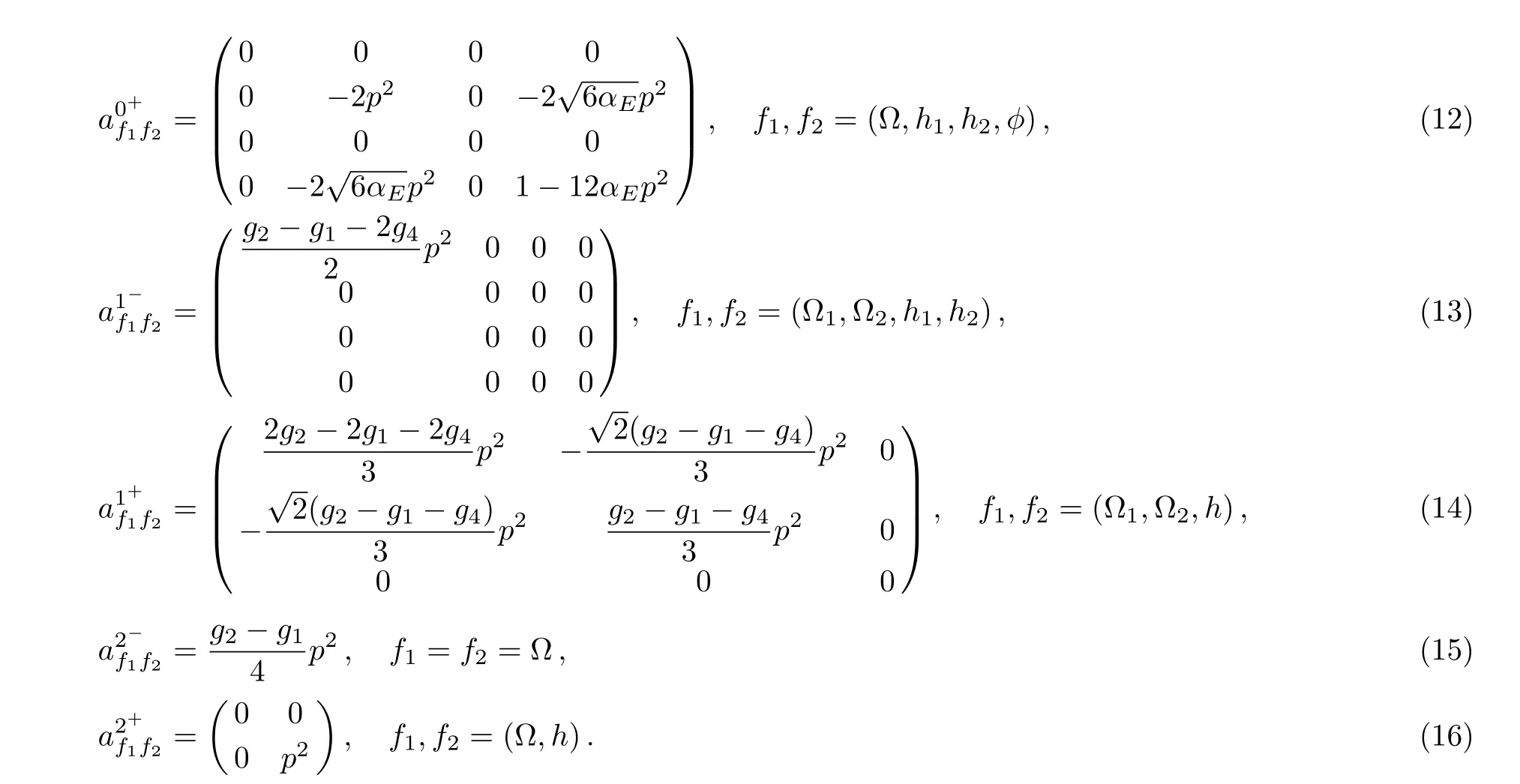
It is obvious that most of the matrices are degenerate,and these degeneracies indicate certain symmetries of the quadratic terms[11]relevant to unphysical degrees of freedom.When considering only the tree-level calculations,we do not need to know the exact gauge- fixing terms and gauge transformations by introducing the Faddeev-Popov ghosts.Instead,we can just apply the specific gauge- fixing conditions by setting the constraints

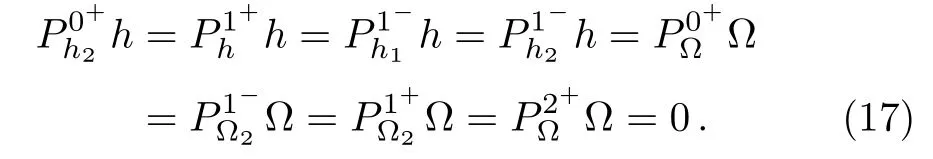
without breaking the field equations,and neglect the corresponding lines in the coefficient matrices.Thus we only need to invert the“reduced” matrices and get the propagators.

The resulting propagators are given as follows in the specific gauge:

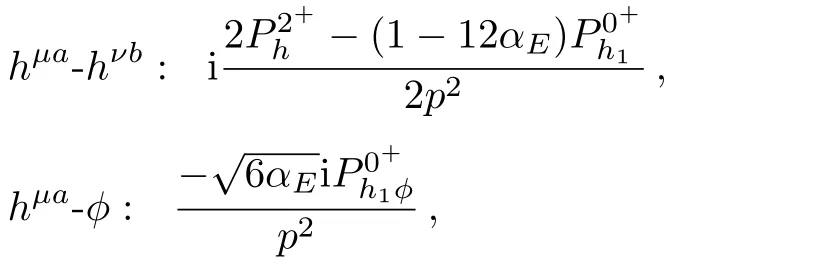
In general,when treating the fields χµaand Ωµabas Yang-Mills gauge fields in GQFT,we can simply add the usual gauge- fixing terms for the gauge-type gravifield χµaand the spin gauge field Ωµab.For simplicity,we take the following explicit forms for their gauge fixing conditions

In such a case,the coefficient matrices of the field equations are given by

Except for the 1+component of the gravifield,all other coefficient matrices are non-degenerate.Thus we are able to inverse the matrices by requiring

and get the propagators:

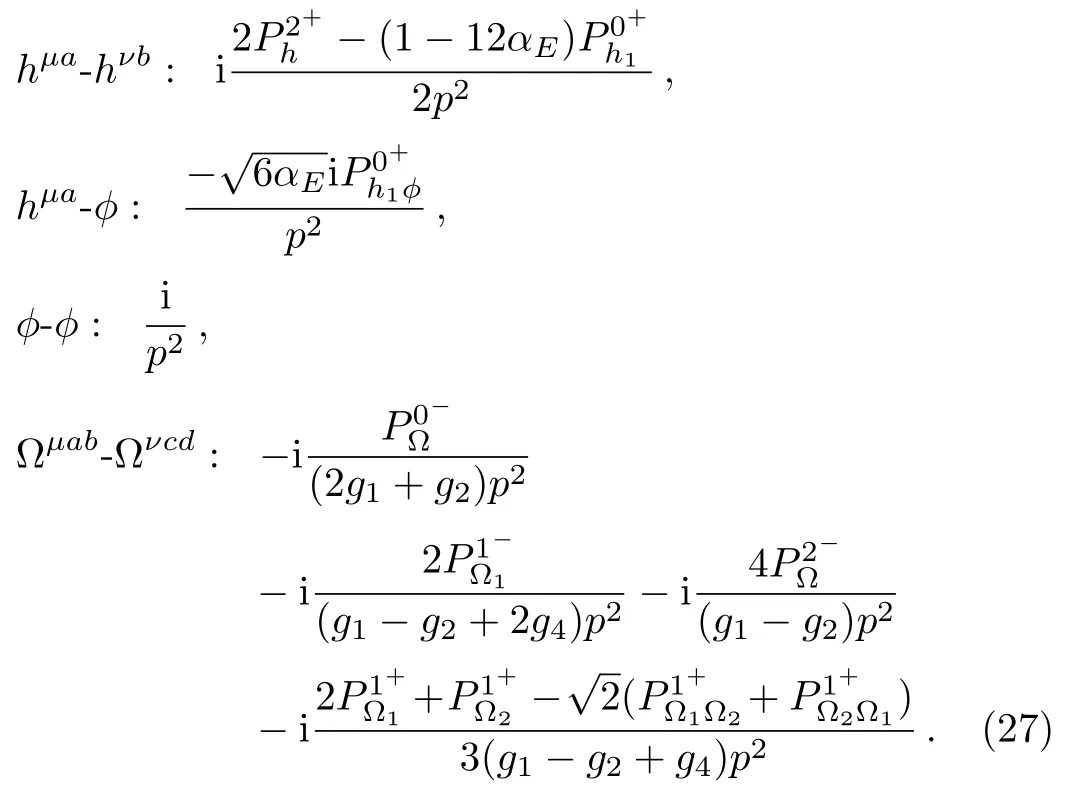
It is seen that in this case the propagator of the gravifield recovers the same one as the case without adding gauge fixing condition,while the propagator of the spin gauge field is modified for the spin 1 component with even parity,which is relevant to the total antisymmetric part of spin gauge field.

It is noticed that there is an intersection term ϕ−h,which is caused as the choice of h and ϕ is not orthogonal.To avoid such a complication,it is useful to rede fine the quantum field

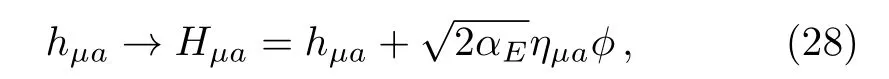
so that the propagator of the field Hµabecomes

which is compatible with the propagator in the usual linear gravity approach[5]up to a gauge term pµpν/p2.If we take the gauge coefficients λ,to be 3/2,the explicit form of the H-H propagator is

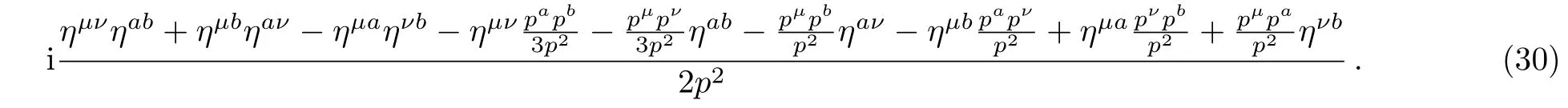
When taking the gauge fixing parameters as follows

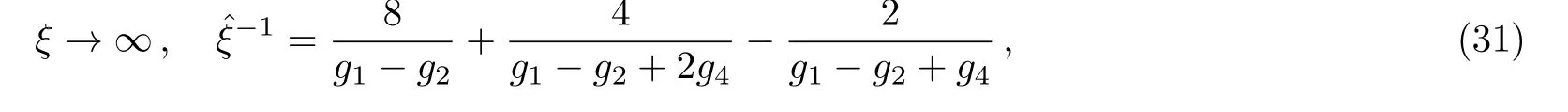
the explicit form of the Ω-Ω propagator is

so that the highest order pole in the propagator isterm,which behaves like a Yang-Mills gauge field propagator.In the following section,we will use the rede fined symmetric quantum gravifield to calculate the physical observable.

4 Gravitational Scattering Amplitude of Dirac Spinor and Modified Newton’s Law with Background Field

Let us now focus on the gravitational interaction between the Dirac spinor field Ψ in the early universe.The leading order vertex of the fermion involves the background field.

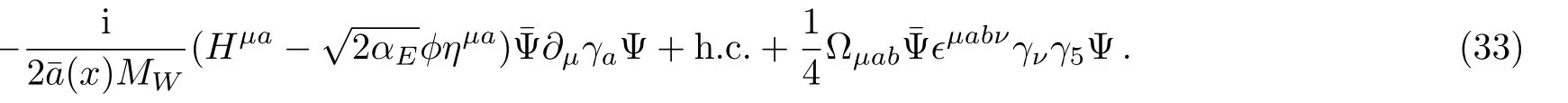
In the momentum space,the background scaling factor is given by

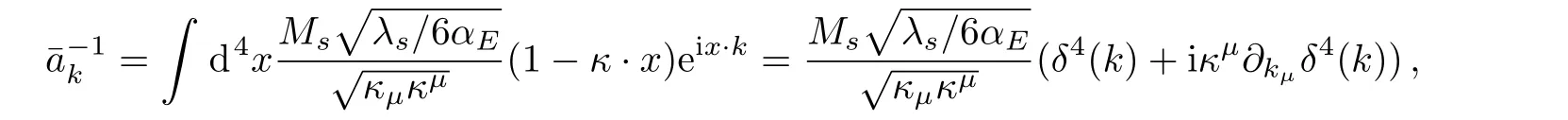
where ∂kµ≡ ∂/∂kµ.Corresponding to Feynman rules shown in Figs.1 and 2.

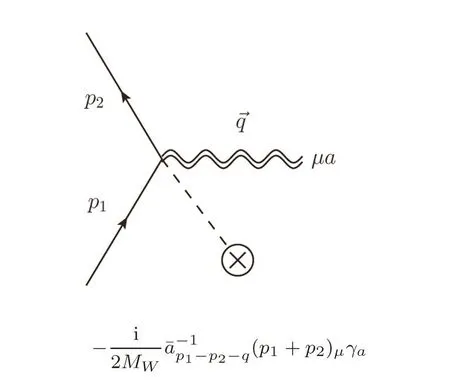
Fig.1 3-vertex for f-f-h.The dashed line connected to the cross is the background.

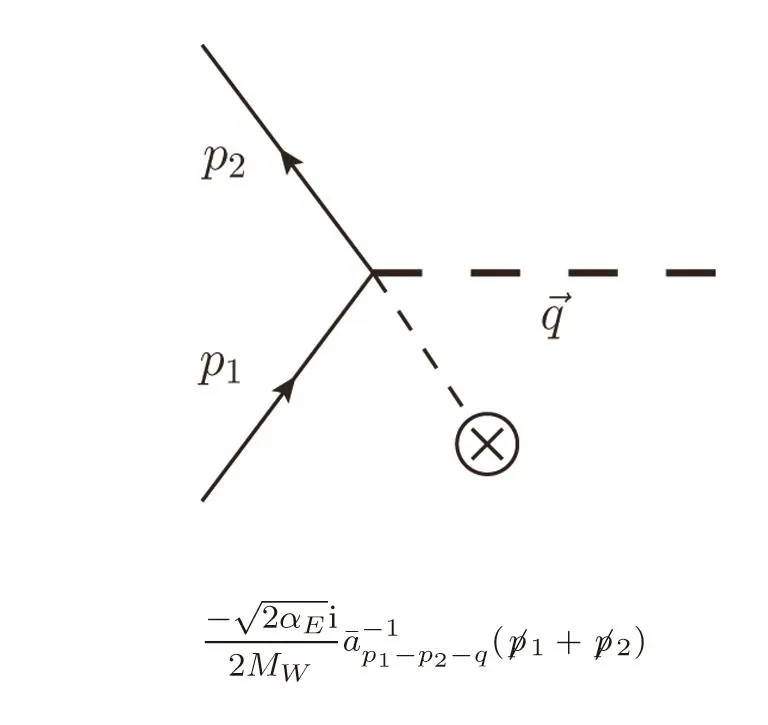
Fig.2 3-vertex for ϕ-ϕ-h.The dashed line connected to the cross is the background.

Note that in calculating the fermion-fermion scatter-ing,the gamma matrix in the vertex is contracted with the two external spinors,which satisfies the equationSo that the couplings to ϕ do not contribute to the tree-level diagrams.For the same reason,the third term from the H propagator does not contribute to the result,either.

The tree level amplitude of the two-fermion scattering,with in-state momenta p1and p2,and out-state momenta p3and p4,is shown in Fig.3

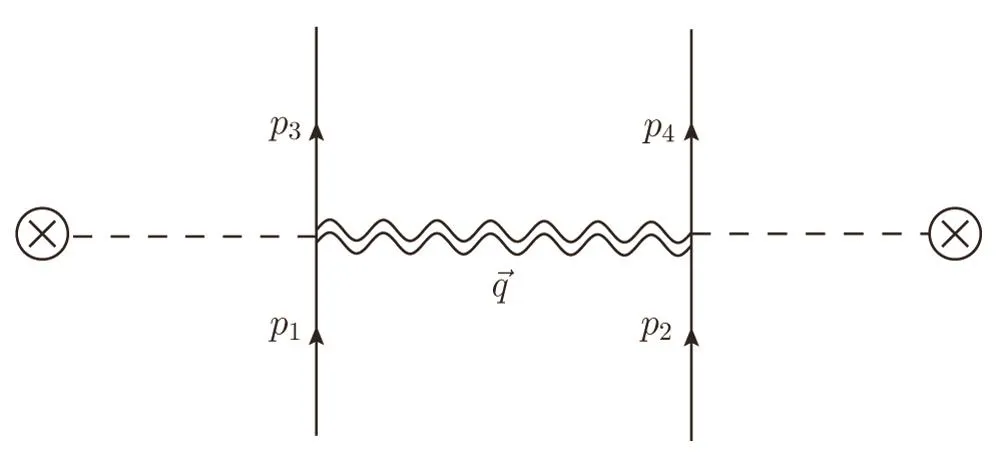
Fig.3 Tree diagram for 2-fermion scattering via gravifield.

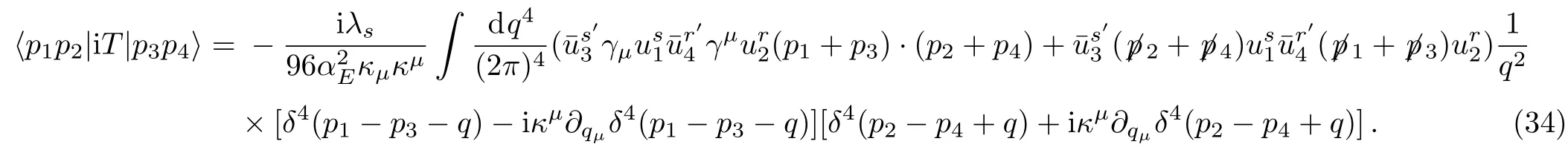
The main purpose is to check the newtonian potential in the early universe with the existence of background field.For the case that all fields are massless,we cannot take a non-relativistic limit to simplify the amplitude.Let us first check the cross section of this scattering process to contract all the spinors.After integrating the momenta of the propagator,the amplitude in Eq.(34)becomes:

The derivatives of δ(p)can be expressed as some functions multiplied by δ(p),thus we can write the second line in Eq.(35)to the following general form

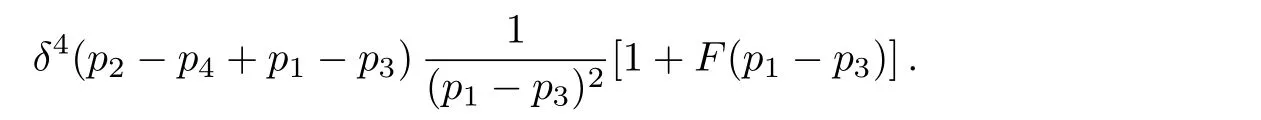
Then our result of the scattering amplitude,except for the overall coefficient and F(p1−p3)term that are related to the background field,is consistent with the leading order result shown in Ref.[14].If we were working in another gauge if xing condition,the difference would be terms proportional to qµqν/q2,contracted with the vertex will gives the termboth of which are vanishing because of the on-shell condition of the external fermions.So our result is indeed gauge independent.

The squared matrix element,after throwing all the spin information,is:

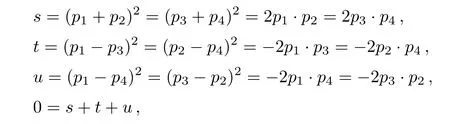
we can simplify Eq.(36)into the follow form

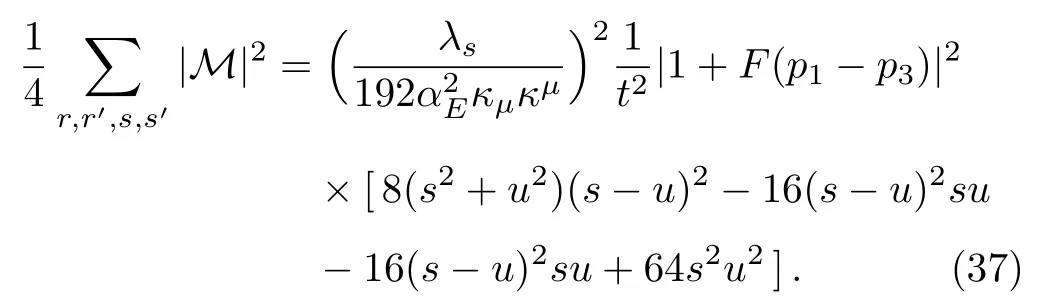
As long as the two massless fermions are not in the same direction,we can always make a Lorentz boost to a centerof-energy frame,so thatWhen taking the weak interaction limit that θ→ 0,we have

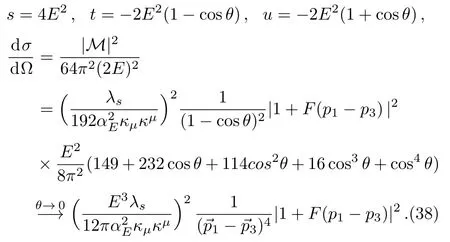
In comparison with the Born approximation of the cross section[16]

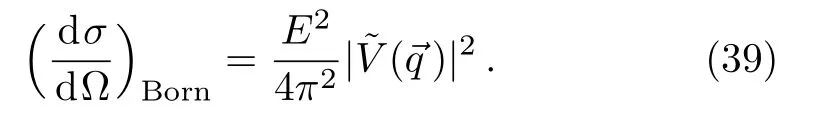
To compare our result with those from the usual Newtonian potential,we identify the factorwith the coefficient of the Einstein equation 8πG.So the relation between αEand Newtonian gravitational constant GNis

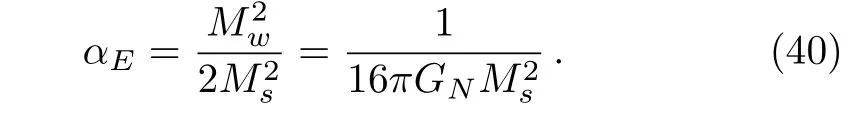
Then we obtain the potential in the momentum space as:

The leading term will contribute to a 1/r potential in the coordinate space.Such a term coincides with the Newton’s law,but it is modified by a factorwhich depends on the size of the inverse of scaling factorIn the early universe,the scaling factor is much smaller,thus the gravitational potential can become much stronger.The modified termcontains the structure of the derivatives of delta functions,we shall investigate its effect elsewhere.

Note that the coefficient 16πGNis four times than the gravitational potential for the massive Dirac fermions.This is because we are working on the massless Dirac fermions.When considering the Dirac fermion getting a mass from spontaneous symmetry breaking,a mass term will be generated.In a unitary scaling gauge condition detχ=1,we need to consider the change of the spinor structure,and an additional

from the third term(30)of the graviton propagator.The massive Dirac fermion allows us to take a non-relativistic approximation

The leading order and next-to-leading-order contributions fromis found to be

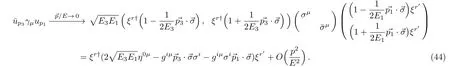
The leading term for µ =0 requires r=r′,which together with Eq.(42)enables us to get a factor 1/4 for the potential(50).The next-to-leading-order term forµ=0 comes from the expansion of E

The next-to-leading order fromµ=i can be simplified to

the spinor formalism can be re-expressed as a four-vector

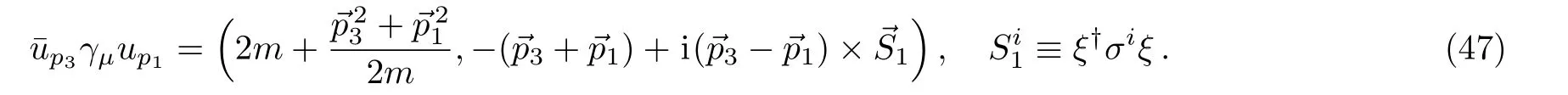
Substituting it into the expression of the amplitude Eq.(34)

we can obtain the total contribution up to next-to-leading order,

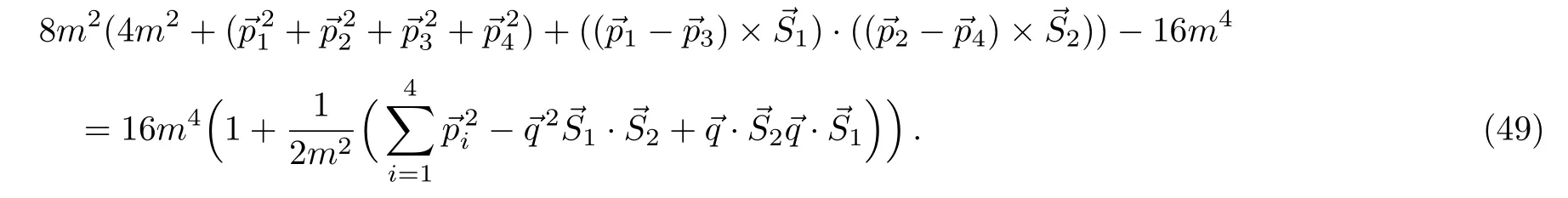
So the potential for massive fermions is

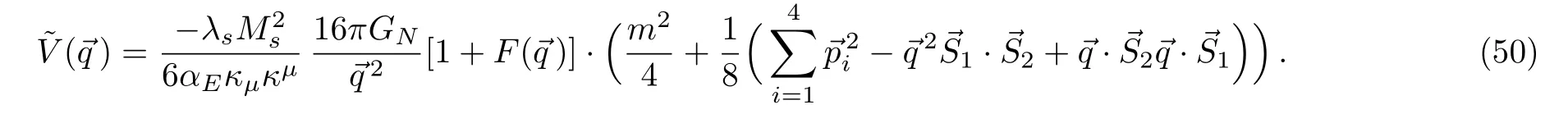
Ignoring the kinematic energies,the next-to-leading order effect is proportional to the inner product of two particles,

If we consider the anti-fermion,its spinor structure is

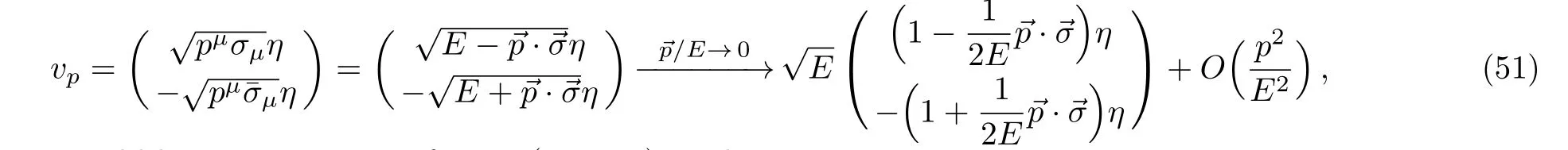
and the vertex would have a minus sign from −(p2+p4)µ.The vertex spinor contraction is

So the there was only an overall minus sign from the momentum,and will be compensated by the commutation of the fermion operator in the Wick contraction,thus the amplitude does not flip sign.The only possible difference lies in spin of the anti-fermion η†σiη.Thus we may use a separate spin notation to distinguish particle and antiparticle

So the next-to-leading order effect between fermion and anti-fermion is

Let us now consider the special case that the two massless ingoing particles are in the same direction.Suppose that their momenta are chosen as follows

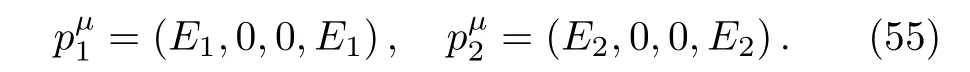
As the overall δ4(p1−p3+p2−p4)guarantees the momentum conservation,the outgoing momenta must be in the same direction.In this case,all the momenta are in the same direction,they are null vectors.So that their product gives zero,namely s=t=u=0.As a consequence,the cross-section becomes vanishing.

5 Scattering Amplitude of the Dirac Spinor via the Spin Gauge Field

It is interesting to consider the scattering amplitude of Dirac spinor via the spin gauge field.The leading order spin gauge interaction of Dirac spinor is given by the totally antisymmetric coupling of the spin gauge field.The vertex Feynman rule in Fig.4 can be derived from the last term in Eq.(33).

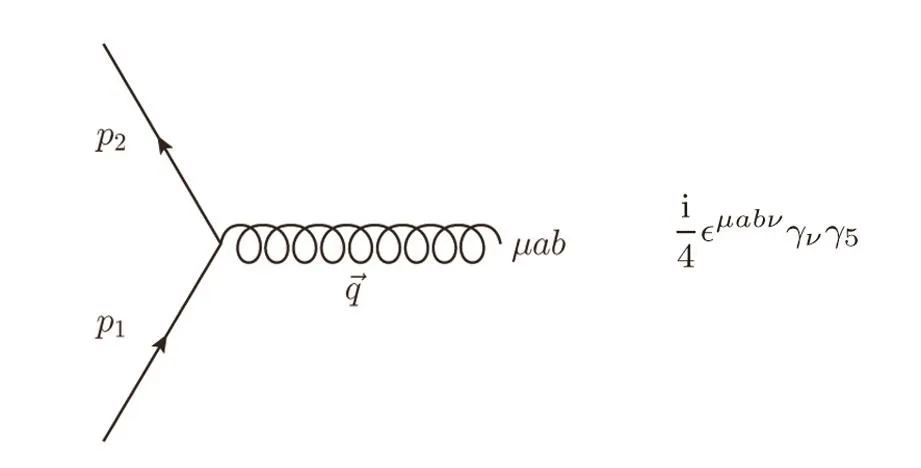
Fig.4 3-vertex for f-f-Ω.

The propagator of the totally antisymmetric part of the spin gauge field is taken the following form

We may rede fine the coupling constants[13]

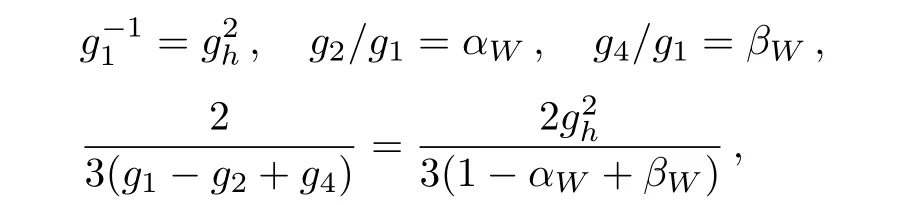
and rede fine the spin gauge field and replace the vertex

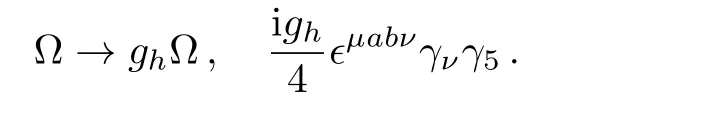
The Dirac spinor scattering amplitude via the spin gauge field is shown in Fig.5.

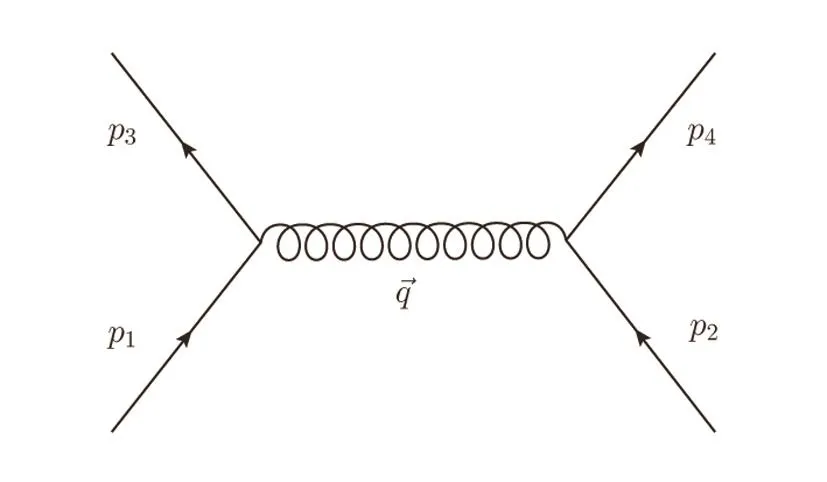
Fig.5 Tree diagram for 2-fermion scattering via spin gauge field.

If the Dirac spinor acquires a mass from some symmetry breaking,we may take the non-relativistic limit of this amplitude.Different from the Coulomb potential where the leading contribution comes fromthe γ5in Eq.(57)will lead to

It is shown that the potential for 2-fermion scattering without spin change can be attractive(repulsive)for aligned spins and repulsive(attractive)for opposed spins,which relies on the sign of the coefficient(1−αW+βW)whether it is positive 1 − αW+ βW> 0(negative 1−αW+βW<0).The potential of the totally antisymmetric field was studied in a different way in Ref.[6],which arrived at the case of negative coefficient 1−αW+βW<0.Such an interaction is independent of the background field.In the early universe,the scaling factor is so small that the gravitational effect becomes dominant to the cross sections.The spin gauge coupling is no longer significant,its cross section is found to be:

When taking the weak interaction limit that θ → 0,we have

which leads to a 1/r potential in the coordinate space.

6 Conclusion

We have investigated the gravitational interactions with the background field in the framework of GQFT.The full action of the GQFT with spin gauge and scaling gauge transformations has been expanded in a nonconstant background field.To the leading order gravitational interactions in GQFT,we have derived the Feynman rules for the propagators and interacting vertices of the quantum fields by using the tensor projection operators.The quantum gravifield has been rede fined to be normalized and diagonal,which leads to an interaction between the Dirac spinor and scalar fields.In the leading order,the scalar interaction with the Dirac spinor vanishes when the massless Dirac spinor are on-mass shell as the external fields.We have calculated the tree-level two Dirac spinors scattering through the gravitational interaction and analyzed its amplitude and cross section.Besides the modified term from the derivative of delta function,the overall amplitude is proportional to the inverse of the scaling factors,which implies that the gravitational potential is much stronger in the early universe.The spin dependence of the gravitational potential in the nonrelativistic case has been analyzed.We have also calculated the interaction between the Dirac spinor and the totally antisymmetric part of the spin gauge field at the leading order,which is similar to the result of the scattering through a vector field,but with a flip sign in the amplitude due to the property of axial vector,resulting in a spin gauge force,which depends on the sign of the coefficient in its quadratic terms.

Appendix A Next-to-Leading Order Quadratic Terms

We have presented the leading order quadratic terms in the context,the following are the higher order terms of the background field.We de fine

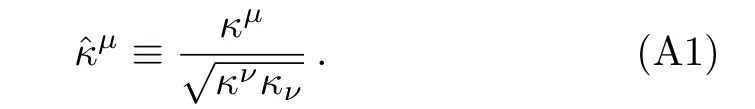
The next-to-leading order quadratic terms for hµa-ϕ are:

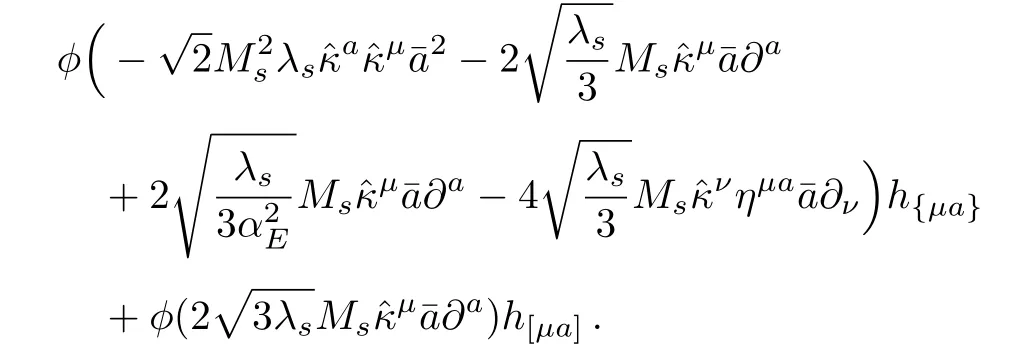
The terms for hµa-wνare:

The terms for ϕ-wµare:

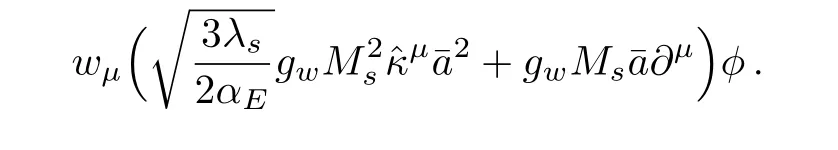
The terms for wµ-wνare:

The terms for ϕ-ϕ are:

The terms for hµa-hνbare:

Appendix B Leading Order Vertices

We have presented the leading order vertices of the fermions in the context,the following are the 3-vertices for the spin gauge field Ωµabwith the rede fined field Ω by a coupling constant:

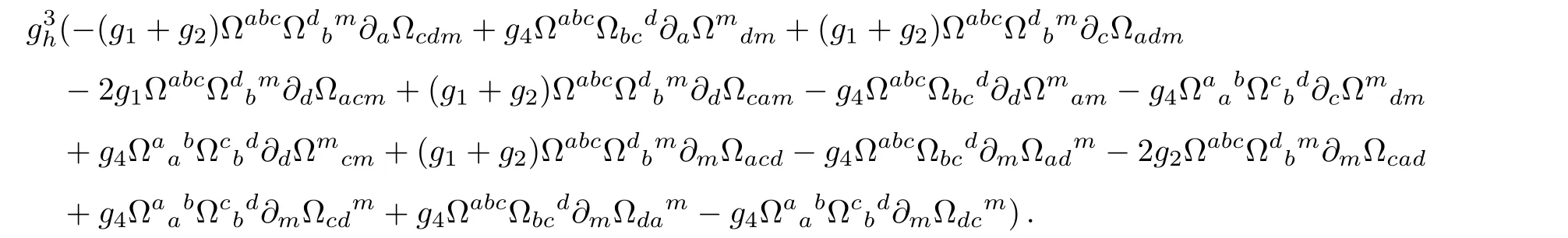
For the gravifield hµainteractions,we have

For the scalar field ϕ,except the pure scalar interaction term 4λsϕ3ϕ,and the scalar and gravifield interactions are found to be,

for h-ϕ-h,and

for h-ϕ-ϕ,as well as

or h-w-ϕ,and

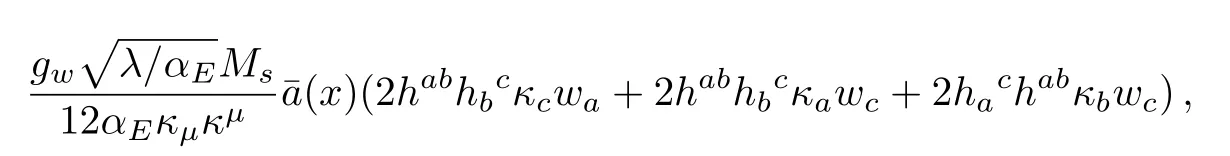
for h-h-w.With coupling to the spin gauge field,we obtain

for h-Ω-Ω.More interactions include

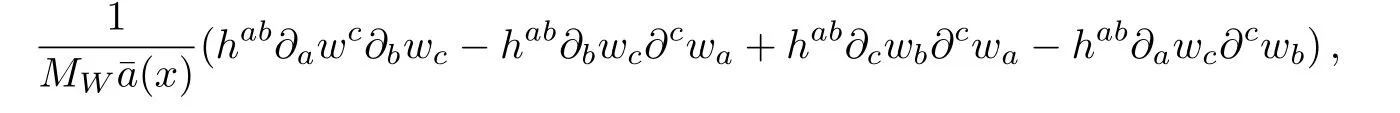
Appendix C Tensor Projection Operators

Here we show the exact expression of projection operatorsfor the spin gauge field,gravifield and scalar,in which we have used the de finitionsfor short.