Jeans Instability of Self Gravitating Dust Cloud in Presence of Effective Electrostatic Pressure
2018-08-02PratikshyaBezbaruahPritamDasPrathanaBorahandNilakshiDas
Pratikshya Bezbaruah,Pritam Das,Prathana Borah,and Nilakshi Das
Department of Physics,Tezpur University,Assam 784028,India
AbstractThe role of viscosity coefficient(η′),coulomb coupling parameter(Γ)and dust mass on the growth of jeans mode is investigated in strongly coupled dusty plasma using equations of Generalized Hydrodynamics(GH)Model.The novel aspect of this work is that the force arising due to electrostatic pressure caused by grain grain interaction has been included in the dynamics of dust particles.This force is found to play a significant role in counter balancing the self gravity effect,thereby reducing the growth rate of jeans instability.The present work may provide more physical insight in understanding the mechanisms behind formation of planetesimals,stars etc.
Key words:generalized hydrodynamics model,interstellar medium,planetesimal
1 Introduction
Plasma and dust comprise a major fraction of the universe.The interesting features manifested by dusty plasma is commonly observed in many astrophysical environments such as in molecular clouds,interstellar and interplanetary regions,solar comets etc.[1]The process of astrophysical object formation is controlled by the interplay of self gravitational and electrostatic forces that operate among the dust grains in molecular clouds or in self gravitating dust clouds.For micron and sub micron sized grains the two forces turn out to be comparable for the range of parameters that are consistent in astrophysical regimes.[2−3]Gravitational instability is a mechanism responsible for the collapse of dust and gas particles present in the dense molecular cloud that eventually leads to planet formation.[4−6]Krishan et al.have mentioned the importance of gravitational instability in large scale structure formation in the universe.[7]It is also true that in many cases gravitational force dominates over electromagnetic force in astrophysical plasmas contrary to the case in laboratory plasma.[8]It is established that for grains with radius rd>1 micrometer,the effect due to self gravity plays a significant role thereby initiating process for gravitational collapse.[1]In astrophysical plasma environment,dust grains may be charged via different mechanisms such as electron-ion collection,secondary electron emission from the grain surface triggered by the highly energetic plasma particles being incident on the grain surface,photo detachment induced by ionizing radiations in space,radioactive charging etc.Several factors like material composition,size and shape of the grain may also determine the nature and extent of charging that a grain undergoes.[9]The charge on dust grains may fluctuate with charging frequency being of the order of mega-Hertz.In our work,dust charge has been taken to be constant as gravitational instability takes place in much lower frequency scale(∼Hz)as compared to the frequency of charge fluctuation.[10]
In the current study,it is assumed that grains are negatively charged due to interaction with background plasmas.Since the analytical model is focused on dealing with a system where gravity and electrostatic forces operate at the same scale,the dust mass and charge of grains are chosen in such a way that the ratiois of the order unity i.e.the forces due to self-gravity and that due to electrostatic force become comparable.At this scale the typical charge of the dust grains in astrophysical environments is around∼102e.[3]
Strongly coupled plasma may be common in various astrophysical objects like white dwarf,neutron star etc.The density in white dwarf stars may be very high.They do not burn fuel in the core and as a result,the star slowly cools down such that the coulomb coupling parameter Γ may exceed 172.[11]It is therefore,important to study various astrophysical phenomena in the strongly coupled regime.Strongly coupled dusty plasmas are of relevance to several Astrophysical situations like H II region of Interstellar Medium(ISM),Interstellar Cloud etc.The coulomb coupling parameter(Γ)de fining the ratio of dust potential to thermal energy can exceed unity in the compact dust configurations that is achieved during the collapse of dust cloud.[12]Two important but counteracting forces that act on the dust particles in Molecular cloud are due to self-gravity and electrostatic potential.The density fluctuation that may arise due to turbulence may lead to an instability when the dust cloud contract under self gravity.When the density of such dust cloud increases,a negative potential develops in the cloud that prohibits the ions to escape from the cloud.The competition between this effective pressure arising due to this potential and the gravitational force ultimately controls the collapse of the cloud that leads to the formation of planetesimal.In such compact dust cloud,the dust density may be very large and form a strongly coupled dusty plasma.Avinash et al.have numerically calculated the density profile of dust in self gravitating astrophysical dust cloud[13]where they have shown that at the center of the dust cloud,the dust density is very large.Thus,the strong correlation effect may be quite relevant during the process of gravitational collapse in Interstellar Medium(ISM).For such region the central density of the dusty cloud is estimated to be∼ 102m−3and for typical dust temperature Td∼ 80 K,the coulomb coupling parameter(Γ)takes a value∼ 1.24.In the strongly coupled regime,the self gravitational effect may be counterbalanced by the force due to the electrostatic repulsion of similarly charged dust particles.It has been shown by several authors that this electrostatic interaction leads to the dust pressure in dusty plasma.[14−15]In strongly coupled dusty plasma,this effective pressure term may play a key role in the formation of large scale structures caused by self gravitational collapse.
Ali et al.have studied the role of jeans frequency and dust temperature on the growth rate of electrostatic mode considering collisional effects in the system of positive,negative and neutral dust and have also discussed the stability of cometary dusty plasma.[8]The role of polarization force and magnetic field on jeans instability has been discussed in detail by Sharma.[16]The author also clarified that in hydrodynamic regime the modified jeans instability condition is unaffected by strong coupling effects.The combined effect of gravity and electrostatic force is better explained in terms of a ratiowhere G is the universal gravitational constant,mdis the dust mass and qdis the dust charge.Pandey et al.have explained the condition for condensation,levitation and dispersion in a system of dust grains considering that the two forces operate at the same scale such that the ratiois of the order unity.[3]Chhajlani et al.have studied the stabilizing effect of magnetic field and time relaxation parameter on the growth of the electrostatic mode in a self gravitating,strongly coupled dusty plasma.[17]Prajapati et al.have reported the stabilizing effect of visco elastic coefficient and dust thermal velocity and destabilizing impact of polarization force on the growth rate of the jeans mode.[18]
In the present paper an analytical expression for growth rate of Jeans mode is derived using equations of Generalized Hydrodynamics model.The effective dust pressure is invoked in the model to take into account the electrostatic repulsion among the dust grains.[11]
2 Theoretical Model
We consider a self gravitating dusty plasma consisting of inertia less electrons,ions and negatively charged massive dust particles,which are in strongly coupled regime(Γ>1).Electrons and ions are assumed to follow Boltzmannian distribution while the dynamics of dust particles is described by momentum equation and continuity equation.In the system,dust particles of constant mass mdwith charge qd=−Zde for negatively charged grains is considered.The equilibrium quasi-neutrality condition ni0=ne0+Zdnd0is satisfied in the system with ni0,ne0,and nd0representing the densities due to ions,electrons and dust respectively.
The motive of the present paper is to investigate the instability of Jeans mode for a viscous,strongly coupled dusty fluid.The system is modeled using the Generalized Hydrodynamics equations in Linear Response formalism.
We assumed electron and ions to be inertia less as their thermal speed is very high in comparison to the phase speed of the perturbations,hence they are in thermal equilibrium and follow Boltzmannian distribution.Thus,the densities for electrons and ions are given as

where ni(e)0being equilibrium ion and electron densities and ϕ is the plasma potential.
The large scale structure formation in the universe may be attributed to the gravitational collapse of dust and gas.The spectra of mass and charge of dust grains may be very wide in astrophysical environment and it is very common to have situation where electrostatic forces compete with gravitational forces such thatIn the regime 1 ≤ Γ ≤ Γc(Γcis the critical coulomb coupling parameter beyond,which the dusty plasma transits to crystalline regime.)dusty plasma behaves as a visco elastic medium.The momentum equation describing such a system for negatively charged dust grains is given as

where,nd,vdare the perturbed dust density and dust velocity respectively.ψ is the gravitational potential being experienced by the grains due to self gravity.η is the coefficient of viscosity.The momentum equation describes the forces experienced by the grains due to electrostatic interaction,self gravitational effect and the pressure gradient force arising due to strong coupling of grains.The last term in right hand side of Eq.(3)describes the dissipative force arising due to intrinsic viscosity of dust fluid.[19]
The strong correlation among the particles interacting via Debye Hückel potentialhas been incorporated in our model by including a force term in the equation of motion for dust particles,which is derived from gradient of the effective electrostatic dust pressure,given aswhere Γ is the coulomb coupling parameter,Nnnis the number of nearest neighbors,Tdis the dust kinetic temperature ndis the dust density,κ is the screening constant.Corresponding to this,an effective temperature term may be de fined as T∗=(Nnn/3)ΓTd(1+ κ)exp(−κ).Earlier the effective pressure term has been considered in several studies related to Dust Acoustic wave(DAW).[13,20]
The continuity equation describing mass transport in the system is given as
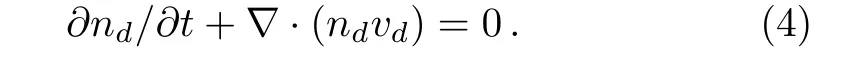
The above set of equations are closed by electrostatic Poisson’s equation

The self gravitational effect appearing in the momentum equation can be dealt in using the gravitational Poisson’s equation

Equations(3),(4),(5),and(6)are linearized such that the perturbed quantities vary aswhere ω is the frequency of the harmonic disturbance andis the wave number.The dispersion relation is derived using the above set of equations in the form

In deriving the above dispersion relation the zero order gravitational field is taken to be zero and a homogeneous equilibrium is thus assumed in the system.However,the neglect of zero order field is difficult to justify in regimes where it is necessary to consider the interplay of electric and gravitational force.[3]In order to overcome this inconsistency,it is necessary to consider that equilibrium is homogeneous asymptotically.In this approach zero order fields are retained and a new field is modeled by combining electric and gravitational fields and the resultant effect is expressed through a new potential ψ0− (qd/md)ϕ0.The Poisson’s equation for the new field is expressed as


At equilibrium when electrostatic force balances gravity,the expression for equilibrium dust density(de fined in Eq.(9))used in our calculation is consistent with the quasi neutrality condition.The parametercorrelates the electrostatic repulsion and the gravitational attraction of the dust particles.
Substituting nd0in Eq.(7)and simplifying we get a quadratic equation for ω

Equation(10)is the final dispersion relation for a self gravitating strongly coupled viscous dusty plasma system.The above dispersion relation is normalized in frequency,mass,charge,density and wave vector by parameters ωpd,md,qd,nd0,and 1/λDrespectively.The normalized form of the dispersion relation is obtained as
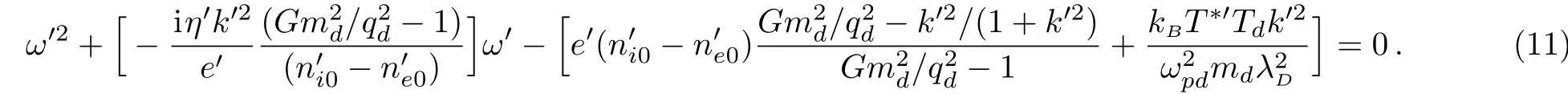

Simplifying the expression of ω′for the condition

the normalized growth rate is obtained as
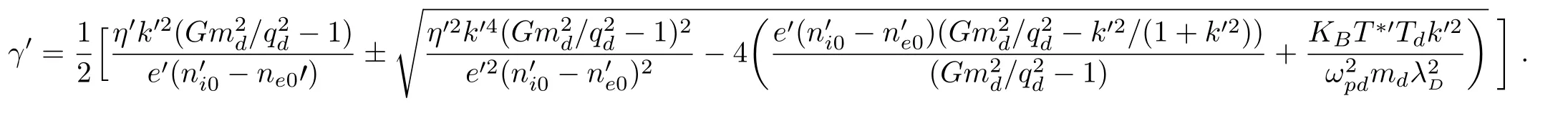
It is observed that the modified growth rate of Jeans instability in the strongly coupled regime is governed by number of physical parameters like mass and charge of dust,intrinsic viscosity and the strength of inter particle interaction,which is a function of coulomb coupling parameter Γ and screening parameter κ.
3 Results and Discussions
The strongly coupled dust grains being affected by the self gravitational pull in the considered parameter regime,results in a continuous increment in the amplitude of the perturbation generated in the system.The unstable equilibrium supports the collapse of the ensemble of dust grains in the systems like dust clouds of H II region,Giant Molecular Clouds(GMC)etc.The outcome of the present work yields an analytical expression on growth rate of Jeans mode as a function of viscosity coefficient,effective temperature through strong coupling parameter Γ and dust mass.
In Fig.1(a)normalized growth rate is plotted against wave vector for different values of normalized viscosity coefficient.The values for η′are taken from the Molecular Dynamics(MD)simulation work of Saigo et al.[21]and the chosen values are compatible with the range of parameters used in the present work.It is observed that the viscosity coefficient is responsible for destabilizing the Jeans mode for the parameter range studied here.
It is mentioned in the Introduction that during the collapse,the density of dust at the center of the dense dusty cloud of H II region may achieve very large value.For our analysis the density,temperature of the dust particles are assumed to be of the order of102m−3and 80 K respectively.The plasma density is approximated for dense dust cloud of H II region with value ni=4.85×1014m−3.[22]The charge on dust grain with radius 1.5 × 10−6m,1.7×10−6m and 1.8×10−6m are 1.1×103e,1.2×103e and 1.3×103e respectively.The values of Coulomb coupling parameterfor the assumed dust density and dust charge are 1.243,1.480,and 1.737 respectively.In the considered parameter regime,Γ is greater then unity that signifies that the system of particles is in strongly coupled phase.For dust cloud of size≤109m[12]in the H II region that has been considered in this paper,the typical value of screening parameterwhere λDis the dusty plasma debye length)may vary in orderforwith the temperature of background plasmaThe electron density is calculated from quasi neutrality conditionFor the given values of nd0,ni0,and Qd,the equilibrium electron density is almost equal to that of ion density.Therefore in the present analysis
Figure 1(b)depicts the variation in growth rate for different values of Coulomb coupling parameter Γ.When the coupling is strong i.e.at high effective temperature the grains are electrostatically bound to each other and can withstand the self gravity to a considerable extent.As a result the growth of the electrostatic mode is suppressed thereby hindering the collapse of the dusty cloud.
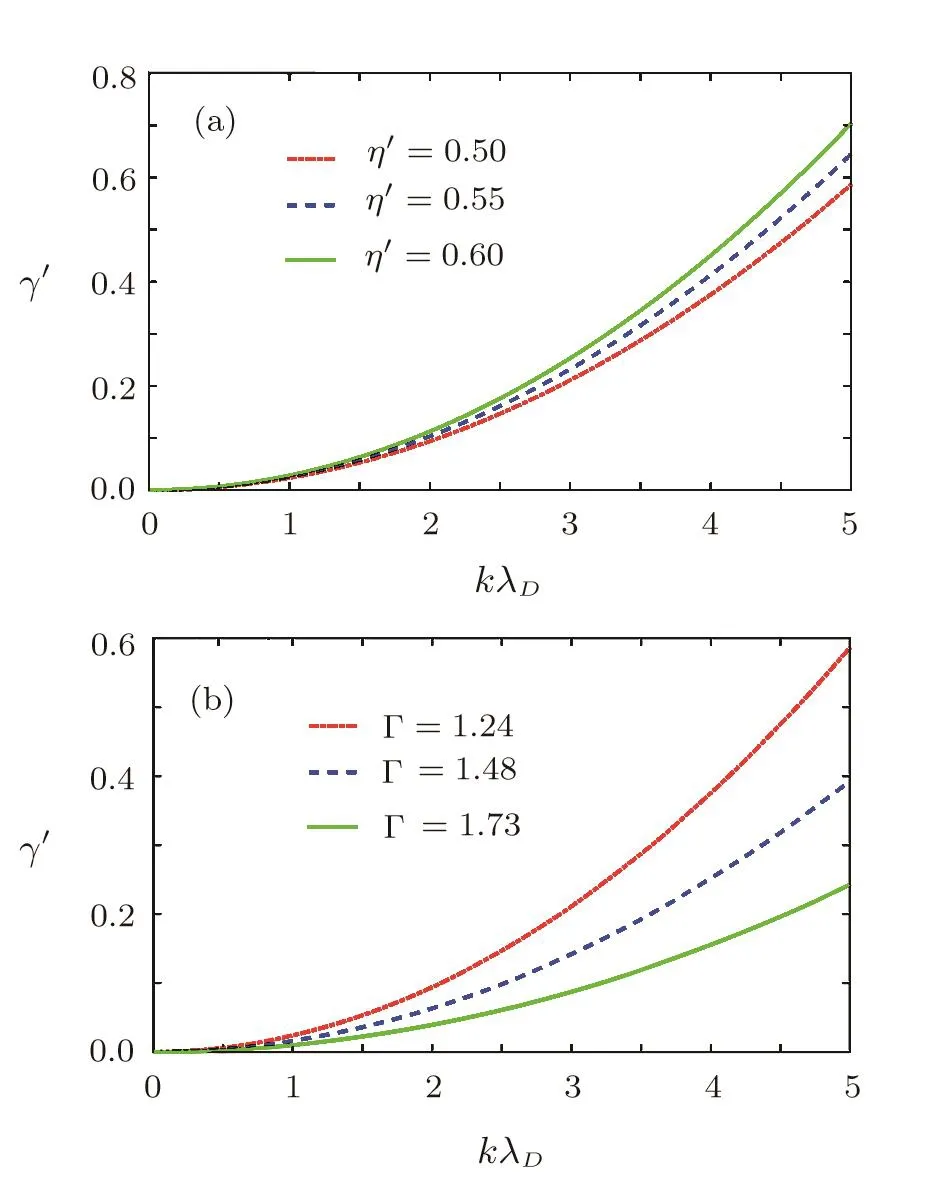
Fig.1 (Color online)(a)Depicts the effect of viscosity coefficient on the growth rate of jeans mode forkg,and Zd0=1100e,ni0=4.85× 1014m−3,Γ =1.243,TD=80 K.(b)Shows the effect of strong coupling parameter on the growth rate of jeans mode formd=3×10−11kg,ni0=4.85×1014m−3,TD=80 K.
Figure 2(a)shows the variation in the growth rate of the electrostatic mode for different values of dust mass.When dust grains are massive,the self gravitational pull exerted by the grains increases.In that case the electrostatic mode turns more unstable leading to an efficient mechanism for collapsing of the system. The effect is predominant in high frequency regime of the electrostatic mode.
A comparison on the unstable nature of the electrostatic mode in presence and in absence of effective dust temperature is presented in Fig.2(b).In presence of effective temperature,system is strongly coupled and the growth is small in comparison to the case in absence of the effective temperature term.Thus,it can be inferred that the strongly coupled dust grains can stabilize the system resulting in a reduced growth of the electrostatic mode.The variation is pronounced only in large frequency regime.

Fig.2 (Color online)(a)Depicts the role of dust mass on the growth rate of jeans mode for η′=0.05,and Zd0=1100e,ni0=4.85×1014m−3,TD=80 K.(b)Presents a comparison on the growth rate of jeans mode in presence and in absence of effective temperature term for dust densityplasma density ni0=4.85×1014m−3.
Pandey et al.[4]have discussed the criterions for Jeans Instability in terms of the parameter de fined by the ratioThey have extensively discussed the conditions for levitation,condensation and dispersion of dust grains.In the present case,it is worth noting that the ratiois of the order unity for the considered parameter regime.The range for dust mass or dust charge chosen in the current analysis for growth rate do not affect the order of the ratio.The dust particles levitate by the balance of electrostatic and self-gravitational fields.In Ref.[4]the authors have mentioned that the frequency of the jeans mode is zero for marginally stable cloudsIn our case also we observe that the real frequency associated with the electrostatic mode to be zero signifying that the counteracting forces balance each other.However,the if nite growth of the electrostatic mode establishes the fact that the equilibrium is unstable.The present instability analysis differs from the work of Pandey et al.in two significant aspects;viz.the inclusion of effective electrostatic pressure that is controlled by coupling parameter and the viscous effect considered in the system.The viscosity coefficient can significantly control the growth rate.The viscous term is mainly responsible for driving the instability in the system.As a result in contrast to Pandey et al.work,where the condition for stable levitation is obtained whenwith no signature for instability,in our case the system is driven unstable in the same limit.The increase in provides a scope to resist the collapse that may be caused due to the effect of self-gravity.In this situationion density in the background has to exceed electron density for maintaining equilibrium.Pandey et al.have elaborated that the increase in ion density as compared to electron density supports a stable levitation with no evidence for instability in the system.In the present analysis of jeans instability,the increase in coupling parameter helps in minimizing the free energy content of the system for a given value of dust mass and viscosity coefficient.However,for the range of Γ considered in Fig.1(b),the growth rate is non zero and finite.This may correspond to an unstable nature of electrostatic levitation of the particles in the dust cloud.
4 Conclusion
The present work is focused on understanding the mechanism of Jeans Instability in a strongly coupled self gravitating,viscous dusty fluid.For understanding the role of strongly correlated dust in the process of collapse,we have calculated the growth rate for the self gravitating mode in Linear Response Formalism for strongly coupled dust grains.The approach undertaken involves the utility of asymptotic homogeneity in the equilibrium to understand the interplay of gravity and electrostatic forces.[3]
The present work has addressed the role of dust charge and hence the coulomb coupling parameter(Γ)in controlling the effective pressure that tries to withstand the collapse caused by self gravity.Thus it becomes possible to analyze the role of strong coupling on stabilizing the self gravitating dusty cloud at a given density when the dust grains are compactly packed.
The present work is an initial effort to visualize how dust mass,viscosity and effective electrostatic pressure control the growth of perturbation in self gravitating dusty cloud when the grains are strongly coupled.To our knowledge,the role of coulomb coupling parameter on Jeans Instability has not been extensively studied,whereas this parameter may play a significant role during the collapse of gravitating dusty cloud.The contribution of various parameters in driving the mode unstable is analyzed.The growth in the perturbation generated in the system is the signature of the unstable equilibrium,which tries to stabilize itself by undergoing a self gravitational collapse.
In the present work we have observed that viscosity coefficient gets coupled with the gravitational term responsible for Jeans instability and contribute towards the enhancement of the growth rate as depicted in Fig.1(b)in contrast to its usual role of stabilizing or damping the modes.Increasing dust mass can also destabilize the jeans mode.Massive grains in a dusty cloud can effectively promote the physical process responsible for the formation of astrophysical objects.The strongly coupled dust grains can retard the growth rate of the system and thus the system is stabilized when Γ is large.
It is observed that the growth of the Jeans mode experiences a hump at a particular value of wave vector,which again depends on viscosity coefficient,coulomb coupling parameter Γ and dust mass.The growth rate progresses smoothly when the system is not strongly coupled i.e.in absence of effective temperature term.The present study may be important to understand the role of strong coupling and intrinsic viscosity of dust fluid in the evolution of massive structures in astrophysical environments.
杂志排行
Communications in Theoretical Physics的其它文章
- A Numerical Investigation of Nanocomposite of Copper and Titanium Dioxide in Water Based Fluid Influenced by Instigated Magnetic Region
- Effects of Thermal Radiation on a 3D Sisko Fluid over a Porous Medium Using Cattaneo-Christov Heat Flux Model∗
- Energy Transfer in the Light-Harvesting Complexes of Purple Bacteria∗
- Effect of Critical Beam Radius on Self-focusing of cosh-Gaussian Laser Beams in Collisionless Magnetized Plasma
- Phase Sensitive Photonic Flash∗
- Self-Similar Solution of Spherical Shock Wave Propagation in a Mixture of a Gas and Small Solid Particles with Increasing Energy under the Influence of Gravitational Field and Monochromatic Radiation
