A Numerical Investigation of Nanocomposite of Copper and Titanium Dioxide in Water Based Fluid Influenced by Instigated Magnetic Region

Z.Iqbal,Ehtsham Azhar,E.N.Maraj,and Zaffar Mehmood

Department of Mathematics,Faculty of Sciences,HITEC University,Taxila 44700,Pakistan

AbstractPresence of external electrical field plays a vital role in heat transfer and fluid flow phenomena.Keeping this in view present article is a numerical investigation of stagnation point flow of water based nanoparticles suspended fluid under the influence of induced magnetic field.A detailed comparative analysis has been performed by considering Copper and Titanium dioxide nanoparticles.Utilization of similarity analysis leads to a simplified system of coupled nonlinear differential equations,which has been tackled numerically by means of shooting technique followed by Runge-Kutta of order 5.The solutions are computed correct up to 6 decimal places.Influence of pertinent parameters is examined for fluid flow,induced magnetic field,and temperature profile.One of the key findings includes that magnetic parameter plays a vital role in directing fluid flow and lowering temperature profile.Moreover,it is concluded that Cu-water based nanofluid high thermal conductivity contributes in enhancing heat transfer efficiently.

Key words:water based fluid,instigated magnetic region,nanoscale particles,Copper and titanium dioxide,stagnation point flow,numerical solutions

1 Introduction

In nature poor heat conductivity of typical fluids e.g.water,ethylene glycol,kerosene oil concoction has turned out to vital restriction in improvement heat exchange forms including traditional fluids.On contrast to fluids some metals such as silver,copper and gold ordinarily have higher heat conductivity.Exploiting high heat conductivity of metals to improve heat conductivity of customary fluids prompted possibility of nanofluids.Suspensions of nanometer measured metal particles in the base fluid concoct such fluids.As a result,the efficient thermal conductivity of nanofluids improves drastically as com-pared to the traditional base fluid.The term nanofluid was at first presented by Choi.[1]Most regularly utilized nanoparticles are prepared from metal oxides like CuO,Al2O3,and TiO2,metals such as Cu,Ag,and Au along with nitride/carbide earthenware production for example AlN,SiN,SiC,and TiC.Base fluids are normally common fluids like water,ethylene glycol,and oil.Nanofluids have ended up being extremely valuable in various mechanical and engineering appliances.Nanofluids are generally utilized as a part of various mechanical and manufacturing apparatuses such as coolants in atomic reactors,mechanical cooling,extraction of geothermal force,advanced medication conveyance frameworks,heat exchangers,indicative tests,disease treatment,and micro scale fluidic applications.[2]Depending on such wide convenience a few exploratory and hypothetical examinations were done to break down various parts of nanofluids.[3−10]

Stagnation points exist at the surface of entity in the stream field where the fluid is conveyed to rest by the object.Stagnation stream depicts the smooth movement close to the stagnation locale where it experiences the most elevated pressure and most noteworthy rate of heat exchange and mass decay.This flow emerges in numerous applications and it has an unmistakable part particularly in transportation commercial enterprises on planning the rockets,air ships,submarines,and oil ships.The stagnation point flows over an extending surface is a traditional issue in fluid mechanics.Hiemenz[11]was the first to examine relentless flow in the vicinity of a stagnation point.From that point forward,countless and numerical studies clarifying different parts of boundary layer stagnation point flow over an extending/contracting surface have been done.[12−17]

For flows where magnetic Reynolds number is not petite,instigated magnetic fields must be considered.[18]It is seen that there are a few astrophysical and geophysical problems in which prompted magnetic field assumes an imperative part in deciding flow features of the problem,specifically, fluid flow in earth’s inside,star arrangement,sunspots,and sunlight based flares in the Sun,turning attractive stars and planetary and sun based dynamo problems.Notwithstanding it,impelled magnetic fields assume a critical part in combination applications with plasma controls.[19]Also actuated magnetic fields could be utilized as a confirmation to anticipate the presence of salty fluid water subsurface seas in Europa and Callisto.[20]The traditional issue of Glauert[21]displayed an original examination for hydro magnetic boundary layer flow past a polarized level plate with uniform magnetic field in the flow heading at the plate.He got arrangement of development arrangements considering both huge what is more,little estimations of the electrical conductivity parameter for the speed and impelled magnetic fields.Impact of induced magnetic field on extensive scale throbbed MHD generator was analyzed by Koshiba et al.[22]Raptis and Soundalgekar[23]researched flow of an electrically directing fluid past a consistently moving unending vertical permeable plate in nearness of consistent heat flux and steady suction considering actuated magnetic field.In another study,Raptis and Masalas[24]considered impacts of impelled magnetic field on flimsy hydro magnetic stream of a thick,incompressible,electrically leading and optically thick emanating fluid past an unending vertical permeable plate.Influence of engendered magnetic field on hydro magnetic free convection flow was exposed by Ghosh et al.[25]Bég et al.[26]got environs non-likeness numerical arrangements for velocity,temperature and actuated magnetic field appropriations in constrained convection fluid metal limit layer stream past a non-leading plate for an extensive variety of attractive Prandtl numbers.Some recent attempts by means of numerical stimulations include Refs.[27–28].

Aggravated by forward specified intriguing tries,present article is an endeavor to look at effect of actuated magnetic field on stagnation point flow of water based Copper and Titanium dioxide nanofluid.Prevailing problem is changed over to arrangement of four coupled differential equations by utilizing nonlinear similarity transformation.The very non straight arrangement of ODEs is handled by shooting technique alongside Runge-Kutta of order 5.The obtained solutions precision is up to 10−6.The impact of noteworthy parameters on velocity,induced magnetic field,nanoparticles temperature and concentration are inspected and uncovered through diagrams and tables.The fundamental accentuation is on investigating the effect of actuated magnetic field with fuse of extending proportion parameter.Moreover,a comparative analysis is carried out for the two types of particles suspended in water based nanofluids.Novel results of present investigation may be useful and beneficial in academic research and nanofluidic problems.

2 Experimental Values and Properties of Nanocomposite Cu-TiO2/H2O

In this investigation,we considering Copper and titanium dioxide nanoscale particles suspended in water base fluid.Moreover,thermal properties of base fluid and nanoparticles are expressed in Tables 1 and 2.

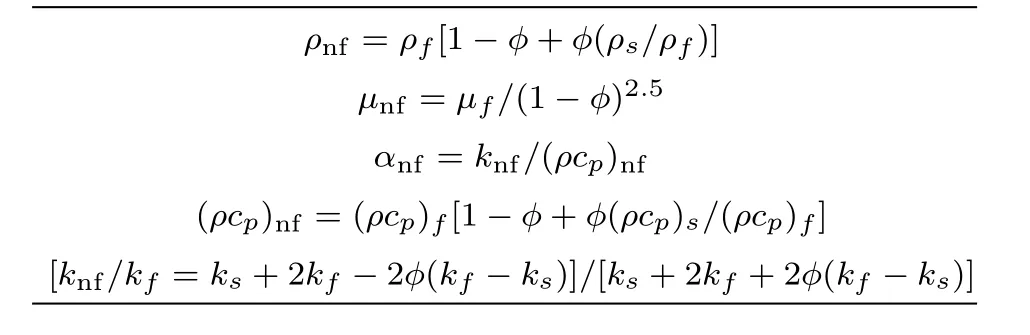
Table 1 According to Ghadikolaei et al.[4]and Iqbal et al.,[7]expression for thermophysical characteristics for nanofluid are:

where(ρcp)sis the volumetric heat capacity of solid nanoparticles,(ρcp)f,(ρcp)nfare volumetric heat capacity of base fluid and nanofluid,respectively.ϕ is the particle volume fraction parameter of nanoparticles,ρfand µfare density and dynamic viscosity of base fluid,respectively.

Table 2 Experimental values of density,specific heat and thermal conductivity for base fluids and nanoparticles(see Ref.[4]Ghadikolaei et al.and Ref.[7]Iqbal et al.)

3 Description of Physical Proble m

We consider steady two-dimensional stagnation point flow towards a linear stretching sheet at y=0.The fluid occupies the region y>0.The free stream velocity is assumed to be Ue(x)=ax and velocity of the stretching sheet is Uw(x)=cx,where a and c are the positive constants.Furthermore we assumed that H is induced magnetic field vector with magnetic field at free stream He(x)=H0x where H0is uniform magnetic field at infinity upstream.Present flow phenomenon is described in following physical flow diagram Fig.1.

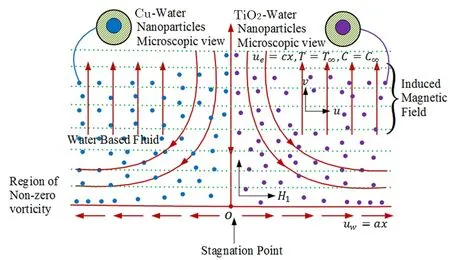
Fig.1(Color online)Physical flow structure.

Governing boundary layer equations for electrically conducting viscous fluid(see Refs.[7]and[15])can be expressed as subject to boundary conditions

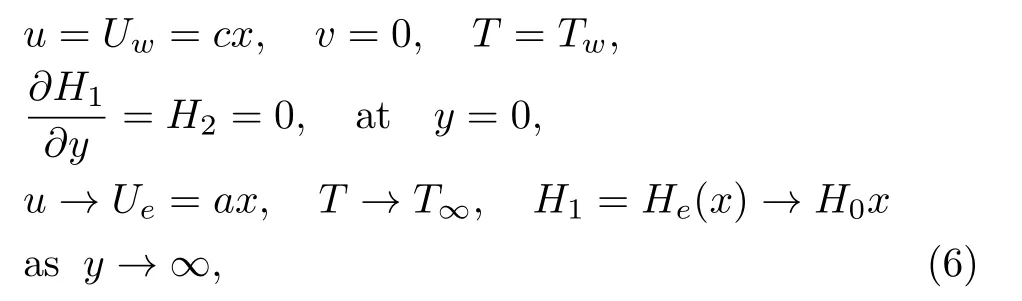
where u,v,H1,and H2are velocity and magnetic components along the x-and y-directions respectively,ρnfis density of the nanofluid,µnfis dynamic viscosity of nanofluid,αnfis thermal diffusivity of nanofluid,T is the temperature of the fluid,knfis thermal conductivity of nanofluid,kfand ksare thermal conductivity of base fluid and solid nanoparticles,respectively.

To further facilitate the present analysis,we introduce the subsequent conventional transformation and dimensionless variable η and f(η)in the following form

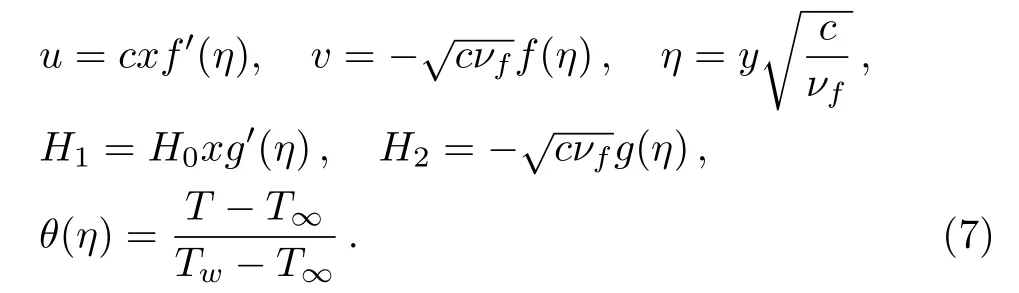
Equations(1)and(2)are identically satisfied and other Eqs.(3)–(5)yield

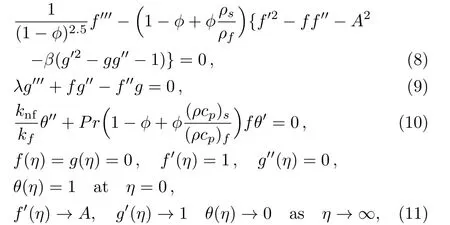
where prime indicates the differentiation with respect to η.Moreover Prandtl number Pr,stretching rate ratio parameter A,reciprocal magnetic Prandtl number λ and magnetic parameter β are de fined as

Physical quantities such as skin friction and Nusselt number are given by

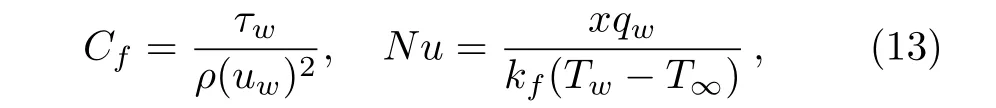
where τwis wall shear stress,qwwall heat flux.Dimensionless form is

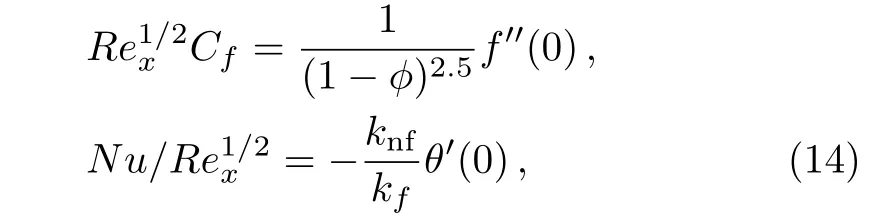
where Rex=uwx/νfis local Reynolds number.

4 Computational Procedure

This segment is dedicated to tackle the solutions of system of nonlinear differential equations numerically.Thus,solution of coupled nonlinear governing boundary layer equations(9),(10),and(11)organized with boundary conditions(12)are computed by means of shooting method along Runge Kutta fifth order method.Firstly higher order nonlinear differential equations(9),(10),and(11)are transformed into a system of first order differential equations and further distorted into initial value problem by labeling the variables as

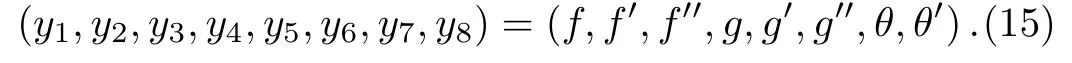
According to the numerical procedure the above system of equations are formulated as:

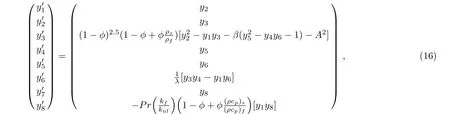
Above mentioned initial value problems have been solved numerically by RK5 method.Suitable values of the unknown and initial conditions are iteratively estimated by Newton method such that the solutions satisfy the boundary conditions at infinity with error less than 10−6.Furthermore,the existing numerical procedure is exemplified in Fig.2.

Fig.2 (Color online)Algorithm flow chart.

5 Theoretical Results Assessment

The effects of several meaningful parameters on fluid flow,induced magnetic field and temperature for Cu-water and TiO2-water nanofluids are displayed and examined in this section.

5.1 Physical Description of Velocity Field

In this regard Figs.3–9 are portrayed to demonstrate the effect of stretching/shrinking parameter A,nanoparticles volume fraction ϕ,reciprocal of magnetic Prandtl number λ and magnetic parameter β for Cu-water and TiO2-water nanofluids,respectively.The analysis of Fig.3 reveals that velocity profile is concave down for A>1 and concave up for A<1 for both types of fluid.A>1 represents the scenario when stagnation velocity is greater than stretching rate whereas the alternate relation between these velocities holds for A>1.

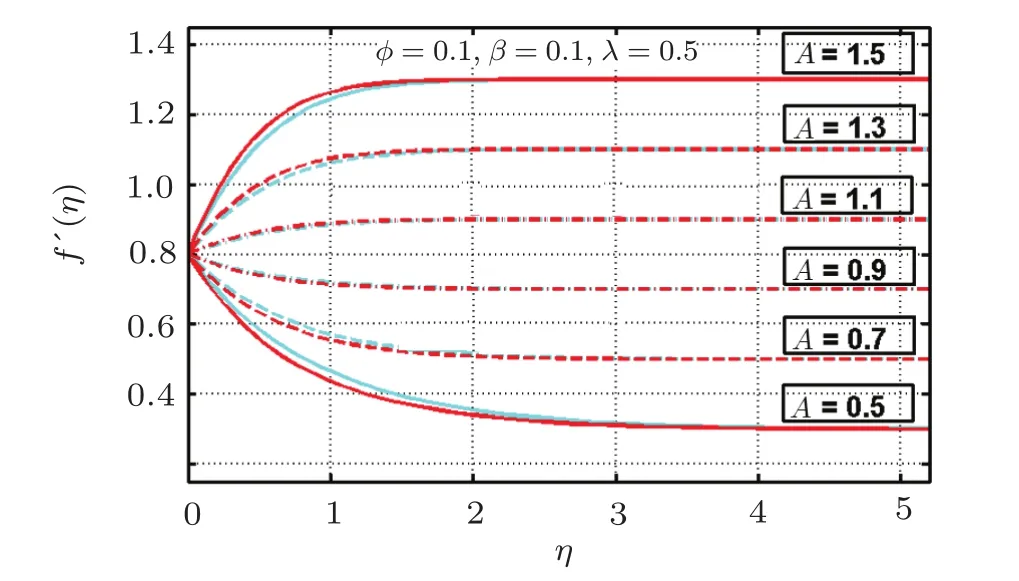
Fig.3 (Color online)Variation of A on f′(η);Red:f′(η):Cu-Water;Cyan:f′(η):TiO2-Water.

Furthermore,boundary layer thickness is more for Cu-water based nanofluid as compared to TiO2-water nanofluid.Variation of nanoparticles volume fraction for two types of metals are displayed in Figs.4 and 5 respectively.It is depicted from these figures that for Cu-water based nanofluid flow reduce for increasing ϕ when A<1 while raising values of ϕ upsurges velocity for case of A>1 see Fig.4.However in case of TiO2-water nanofluid as shown in Fig.5 the rise in ϕ initially lessen fluid flow but latterly contributes in rising it when A<1.An opposite trend is witness for A>1 i.e.,for ϕ=0.05 fluid flow upsurges but for ϕ=0.20 it reduces.

Figure 6 is devoted to examine the effect of λ for two classes for metal nanoparticles suspended fluids.It is observed that velocity appears to be a decreasing function of λ for A<1 and a rising function of it for A>1 for Cu as well as TiO2water based nanofluids.This happens mainly because increase in λ being the ratio of magnetic diffusivity to kinematic viscosity represents the rise in magnetic diffusivity which as a consequence results in lowering momentum boundary layer thickness and velocity for A<1.

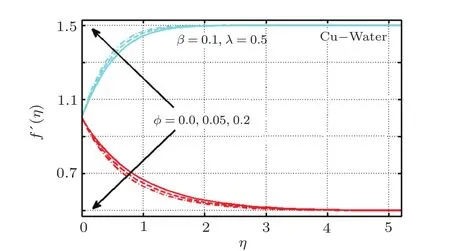
Fig.4 (Color online)Variation of ϕ on f′(η)for Cu-H2O;Red:A=0.5;Cyan:A=1.5.

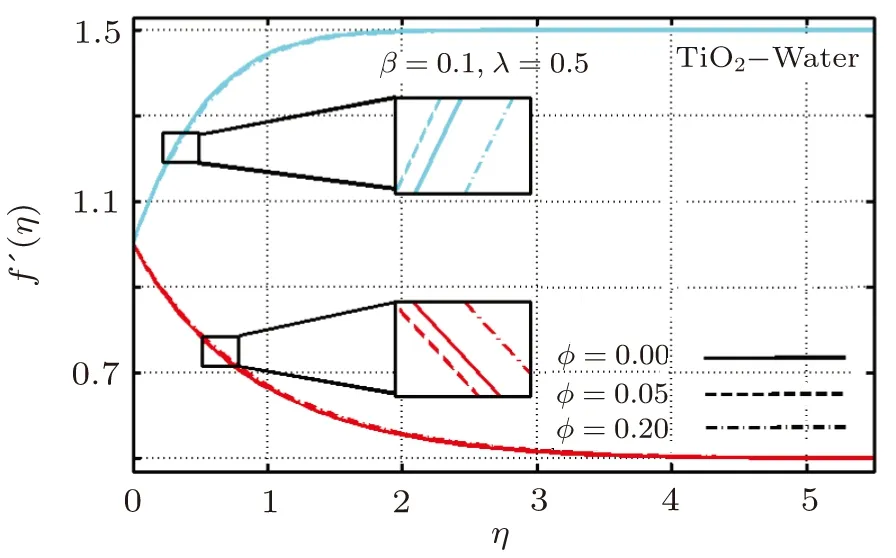
Fig.5 (Color online)Variation of ϕ on f′(η)for TiO2-H2O;Red:A=0.5;Cyan:A=1.5.

Fig.6 (Color online)Variation of λ on f′(η)for Cu-H2O;Red:A=0.5;Cyan:A=1.5.

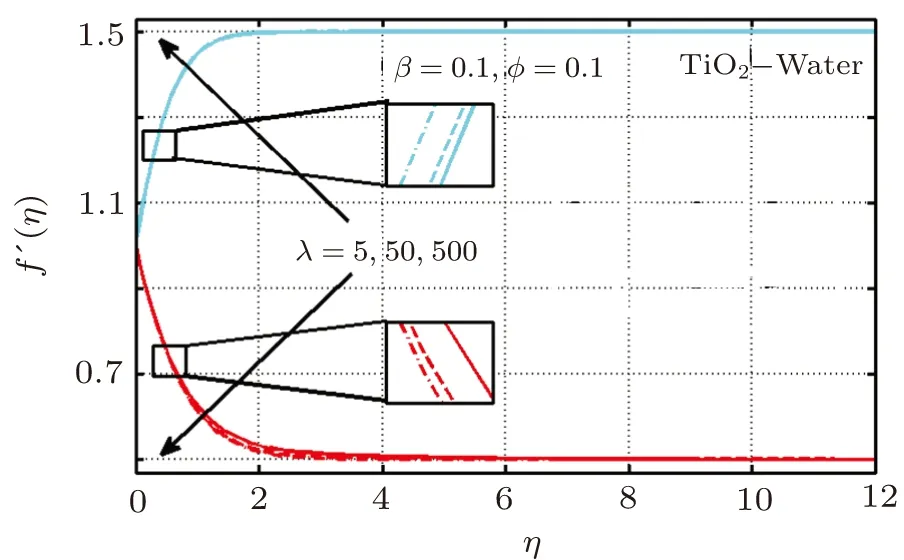
Fig.7 (Color online)Variation of λ on f′(η)for TiO2-H2O;Red:A=0.5;Cyan:A=1.5.

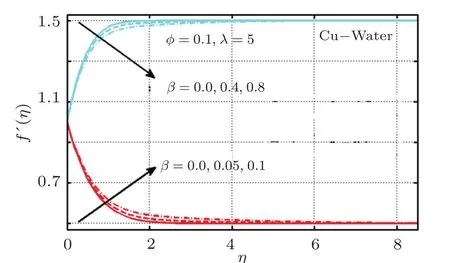
Fig.8 (Color online)Variation of β on f′(η)for Cu-H2O;Red:A=0.5;Cyan:A=1.5.

Similar trend is witnesses for TiO2with a slight variation in magnitude see Fig.7.Influences of magnetic parameter on both types of nanofluids flow are portrayed in Figs.8 and 9.Study of these figures reveals that fluid velocity appears to be a rising relation with β.It shows that magnetic field strength contributes in rising momentum boundary layer thickness and fluid flow.

Fig.9 (Color online)Variation of λ on f′(η)for TiO2-H2O;Red:A=0.5;Cyan:A=1.5.

5.2 Physical Description of Induced Magnetic Field

Induced magnetic field behavior examinations for various significant parameters in case of Cu and TiO2metallic particles are shown through Figs.10–16.It is observed that stretching parameter contributes in lowering induced magnetic field for both types of metal particles.However,this decrease is more evident for Cu-water based nanofluid as compare to TiO2-water based nanofluid see Fig.10.

Effect of nanometal particles volume fractions are demonstrated in Figs.11 and 12 for copper and titanium dioxide nanoparticles,respectively.These graphical results reveal that the rise in ϕ for Cu contributes in rising induce magnetic field when A<1 and a reduction is observed for case of A>1 as displayed in Fig.11.However from Fig.12 it is concluded that TiO2nanoparticles volume fraction initially shows the similar trend as of Cu but for ϕ=0.20 the behavior alters for both studies i.e.,A<1 and A>1.

Fig.10(Color online)Impact of A on g′(η);Blue:g′(η):Cu-Water;Magenta:g′(η):TiO2-water.

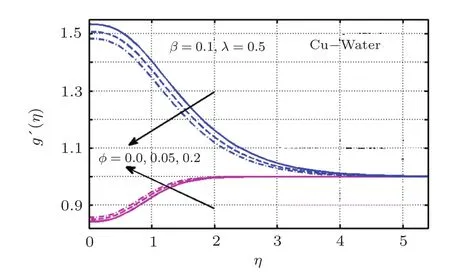
Fig.11 (Color online)Variation of ϕ on g′(η)for Cu-H2O;Blue:A=0.5;Magenta:A=1.5.

Fig.12(Color online)Variation of ϕ on g′(η)for TiO2-H2O;Blue:A=0.5;Magenta:A=1.5.

Figure 13 illustrates the impact of reciprocal magnetic prandtl number on induced magnetic field for Cu and TiO2nano metals.It is revealed that λ contributes in rising induced magnetic field initially or both types of metals nanoparticles and afterwards a decrease in witness keeping A<1.A reverse trend is reported for the case of A>1.Furthermore,a slight change in magnitude is noticed for two types of nanoparticles in Fig.14.

Fig.13 (Color online)Variation of λ on g′(η)for Cu-H2O;Blue:A=0.5;Magenta:A=1.5.

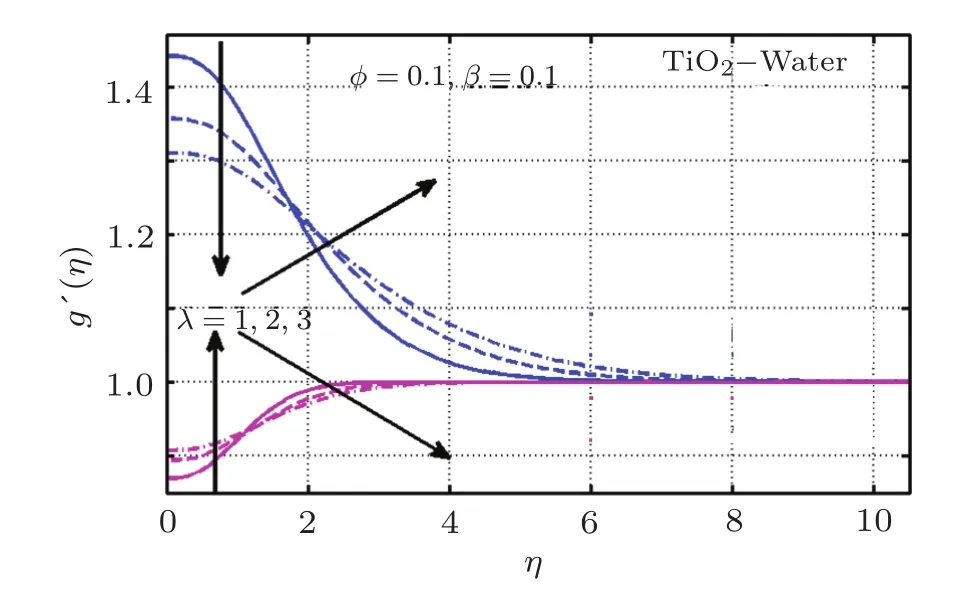
Fig.14(Color online)Variation of λ on g′(η)for TiO2-H2O;Blue:A=0.5;Magenta:A=1.5.

It happens mainly because the increase in λ indicates an increase in magnetic diffusivity as compare to viscous diffusivity,which leads to rise magnitude of induced magnetic field.Figures 15 and 16 are plotted to visualize the effect of magnetic parameter.It is seen that for both types of nanoparticle suspended fluids induced magnetic field lowers with a rise in β for A<1.This decrease is more in TiO2as compared to Cu.Moreover,it upsurges for increasing values of magnetic parameter for A>1.Notably,this increase is more significant in sense of magnitude for case of TiO2as compared to Cu.This happens due to the fact that magnetic parameter is the ratio of magnetic field magnitude to stretching velocity,thus an increase in β showed altered results for A<1 and A>1.Physically it indicates that induced magnetic field is effected by the stretching ratio.

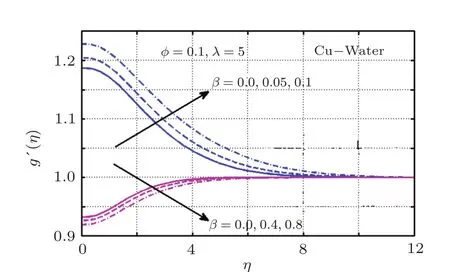
Fig.15 (Color online)Variation of β on g′(η)for Cu-H2O;Blue:A=0.5;Magenta:A=1.5.

Fig.16 (Color online)Variation of β on g′(η)for TiO2-H2O;Blue:A=0.5;Magenta:A=1.5.

5.3 Stream Pattern for Velocity and Induced Magnetic Field

The fluid flow and induced magnetic field patterns are displayed in contour plots for Cu-water and TiO2-water nanofluids from Figs.17 and 18.It is evident that symmetry about vertical axis exists for fluid flow as well as induced magnetic field,respectively.

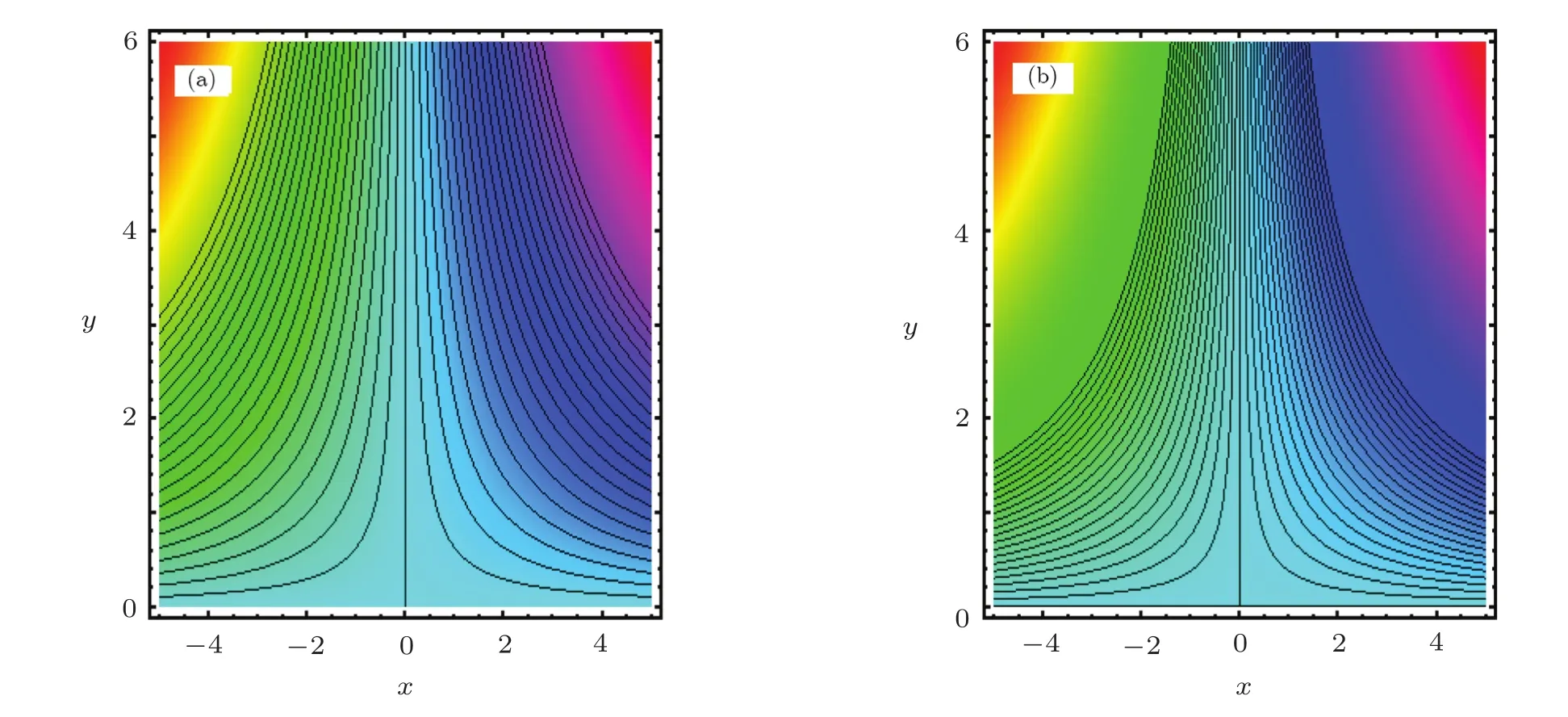
Fig.17 Stream pattern for(a)velocity;(b)induced magnetic field for Cu-H2O when ϕ=20%.

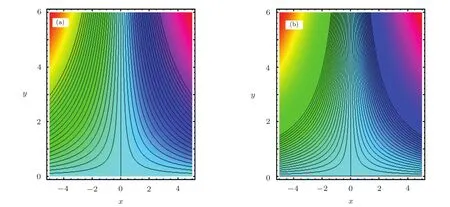
Fig.18 Stream pattern for(a)velocity;(b)induced magnetic field for TiO2-H2O when ϕ=20%.

5.4 Physical Description of Temperature Profile

Figures 19–21 are devoted for comparative study of temperature profiles of Copper and titanium dioxide water based nanofluids.Figure 19 exposed that temperature and thermal boundary layer thickness enhances with the usage of both types of nanofluids.Moreover,it shows that this increase in temperature is more in Cu as compared to TiO2water based nanofluid.Influence of magnetic parameter is portrayed in Fig.20,which demonstrates a temperature reduction for rising values of β.The reason behind it is the fact that β contributes in rising velocity as well as momentum boundary layer and as a consequence thermal boundary layer and temperature decreases.It is noted that temperature decreases more for titanium dioxide than copper nanoparticles.Figure 21 illustrates the effect of λ on temperature profile.Here temperature appears to be an increasing function of λ and this increase is more significant for Cu nanoparticles.Here it is worth mentioning that reciprocal of magnetic parameter acts like a resistive force,which decelerates fluid flow and upsurges fluid temperature.

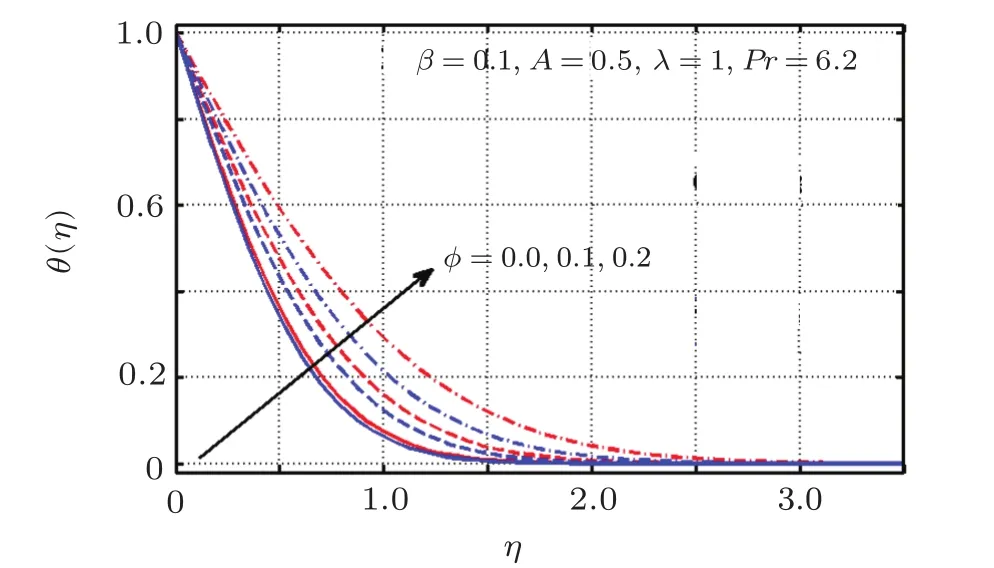
Fig.19 (Color online)Variation of ϕ on θ(η);Blue:TiO2-Water;Red:Cu-Water.

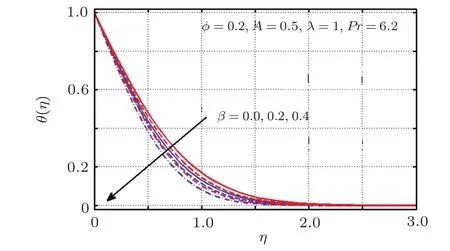
Fig.20 (Color online)Variation of β on θ(η);Blue:TiO2-Water;Red:Cu-Water.

Table 3 Influence of physical parameters on skinfriction and Nusselt number for Cu-Water.

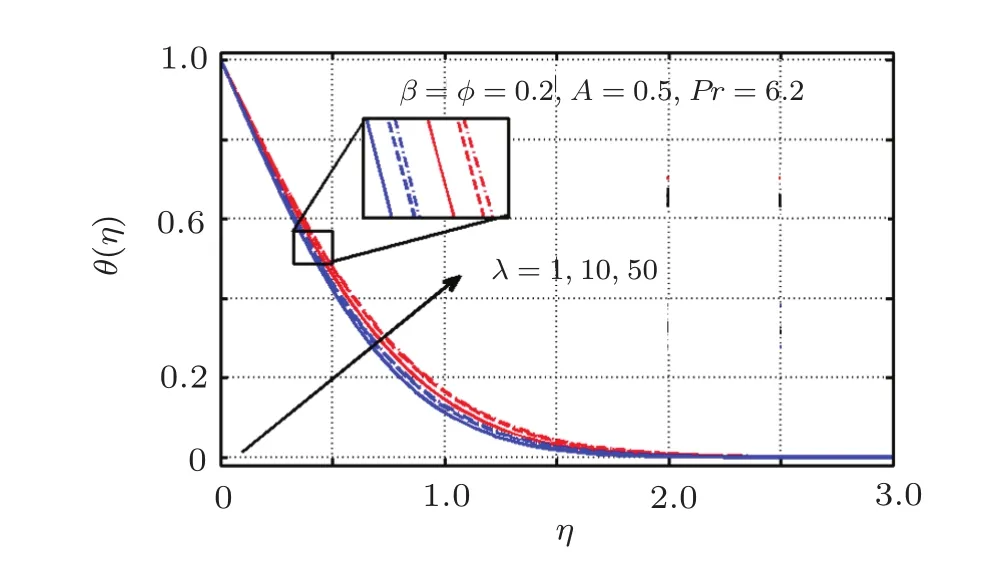
Fig.21(Color online)Variation of λ on θ(η);Blue:TiO2-Water;Red:Cu-Water.

Table 4 Influence of physical parameters on skinfriction and Nusselt number for TiO2-Water.

Tables 3 and 4 are presented to examine the effect of magnetic parameter β and reciprocal of magnetic prandtl number λ in absence and presence of Copper and titanium dioxide nanoparticles for rising values of volumetric fraction.From these tables it is evident that skin friction decreases as magnetic parameter rises while it reduces for rising values of λ.In presence of Cu and TiO2nanoparticles same trend is witness with the rise in magnitude.This rise in magnitude is increased for rising nanoparticles volumetric fraction.Moreover,magnitude of skin friction and Nusselt number is more for Cu than TiO2nanoparticles.

Skin friction coefficient and Nusselt number are plotted for distinct values of important parameters in Figs.22–25.Figures 22 and 23 are skin friction graphs for Cu and TiO2plotted against volumetric fraction for rising values of magnetic parameter.These plots reveal that skin friction rises with the rise in ϕ while it lessens for rising magnetic parameter.Same trend is witness for TiO2with the only difference in raised magnitude scale.Furthermore,Nusselt number represents the heat flux at the surface.It is plotted against ϕ for rising values of β for the case of Cu and TiO2nanoparticles as shown in Figs.24 and 25,respectively.It is observed that Nu rises for increasing values of ϕ as well as magnetic parameter.Moreover this rise is more in magnitude for Cu-water based nanofluid(see Fig.25).

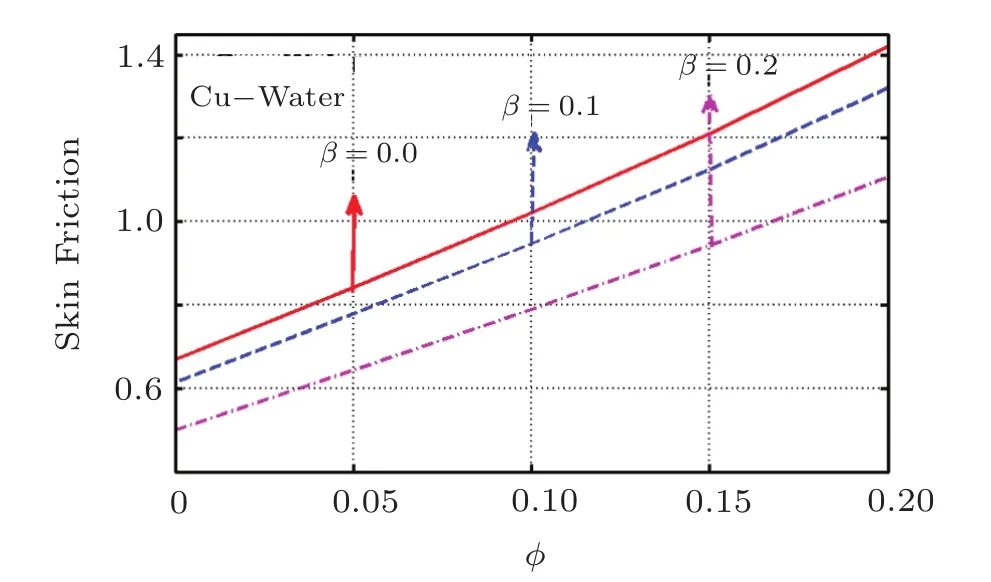
Fig.22 (Color online)Variation of β on Cfagainst ϕ for Cu-H2O.

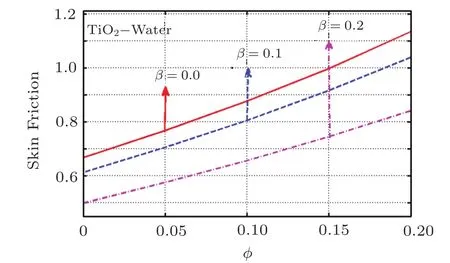
Fig.23 (Color online)Variation of β on Cfagainst ϕ for TiO2-H2O.

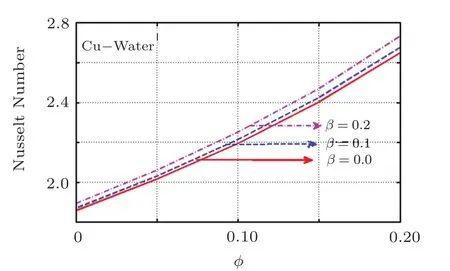
Fig.24 (Color online)Variation of β on Nuxagainst ϕ for Cu-H2O.

Fig.25 (Color online)Variation of β on Nuxagainst ϕ for TiO2-H2O.

6 Conclusion and Novelty of Article

In present article comparative study was performed for two distinct metal nanoparticles namely,Copper and Titanium dioxide.These particles were chosen due to their significance in industry and manufacturing processes.Numerical investigation was performed for stagnation point flow over a linearly stretching surface in presence of induced magnetic field.Governing flow equations were reduced to system of differential equations by utilizing of similarity analysis.The reduced nonlinear coupled system was tackled numerically by means of shooting technique.Numerical analysis was performed in computational software MATLAB.From the above mentioned numerical investigation it was concluded that the usage of metallic nanoparticles in water based fluid was effective in improving thermal conductivity of the water.Cu nanoparticles were more efficient that TiO2nanoparticles.Nanoparticles volumetric fractions effected fluid flow and induced magnetic field significantly.Magnetic parameter and reciprocal of magnetic Prandtl number effected the temperature profile in an opposite manner to each other.Skin friction was an increasing function of ϕ and a decreasing function of magnetic parameter.Nusselt number seemed to be an increasing function of magnetic parameter and ϕ.Novel results of present investigation may be useful and beneficial in academic research and nanofluidic problems.