Quantifying Discriminating Strength for Gaussian States∗
2018-08-02RuiFenMa马瑞芬XiaoFeiQi齐霄霏andJinChuanHou侯晋川
Rui-Fen Ma(马瑞芬), Xiao-Fei Qi(齐霄霏), and Jin-Chuan Hou(侯晋川)
1Department of Mathematics,Shanxi University,Taiyuan 030006,China
2Department of Mathematics,Taiyuan University of Science and Technology,Taiyuan 030024,China
3Institute of Big Data Science and Industry,Shanxi University,Taiyuan 030006,China
4Department of Mathematics,Taiyuan University of Technology,Taiyuan 030024,China
AbstractThe discriminating strength DS(ρAB)induced by local Gaussian unitary operators for any(n+m)-mode Gaussian state ρABis introduced in[Phys.Rev.A 83(2011)042325].In this paper,we further discuss the quantity by restricting to Hilbert-Schmidt norm.The analytic formulas of DSfor two-mode squeezed thermal states and mixed thermal states are given.Then,the relationship between DS(ρAB)and DS((I ⊗ Φ)(ρAB))for some special Gaussian channels Φ is discussed.In addition,DSis compared with Gaussian entanglement for symmetric squeezed thermal states.
Key words:Gaussian states,discriminating strength,Gaussian unitary operators,quantum correlations
1 Introduction
One of the main tasks of quantum information theory is to quantify the entanglement and the quantum correlation(QC)of quantum states.Entanglement lies at the heart of this field,[1−2]but it does not account for all possible quantum correlations contained in a bipartite system.QC had begun to attract increasing interest after the suggestion that they might constitute key resources for quantum information and computing tasks.There are quantum correlations beyond entanglement,such as quantum discord(QD),[3−6]measurement-induced nonlocality(MIN),[7−9]and measurement-induced disturbance(MID)[10−11]for discrete-variable systems.Note that,QD,MID,and MIN are established by the local or two-sided von Neumman measurements.For continuousvariable systems,Giorda,Paris,[12]and Adesso,Datta[13]independently gave the de finition of Gaussian QD for twomode Gaussian states and discussed its properties.For other related results,see Refs.[14–20]and the references therein.
On the other hand,in Ref.[21]the authors de fined a family of entanglement monotones by means of suitable local unitary operations.After then,QCs based on local unitary operations in finite dimensional systems were discussed in Ref.[22–24].In Ref.[25],the authors gave a discriminating strength measure of Gaussian states by local Gaussian unitary operations for continuous variable systems and discussed its properties.
In this paper,we will further discuss discriminating strength proposed in Ref.[25].The paper is organized as follows.In Sec.2,we recall the concepts of Gaussian states and Gaussian unitary operators.In Sec.3,by restricting the metric to Hilbert-Schmidt norm,we further discuss the properties of the discriminating strength DS(ρAB)proposed in Ref.[25]for any(n+m)-mode Gaussian state ρAB,and concrete formulas for two-mode squeezed thermal states and mixed thermal states are obtained.Section 4 is devoted to comparing DSwith Gaussian entanglement for symmetric squeezed thermal states.
2 Gaussian States and Gaussian Unitary Transformations
For any α =(α1,...,αn)t∈ Cn,denote by
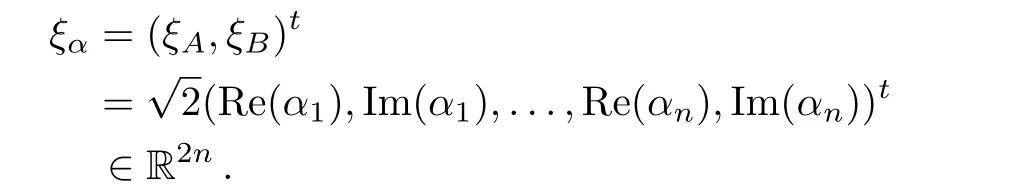
Gaussian StatesAn n-mode Gaussian state ρ can be described by its characteristic function
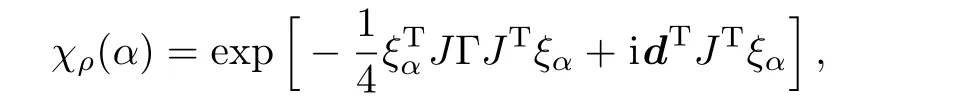
Now assume that ρABis any(n+m)-mode Gaussian state.Then the CM Γ can be written as
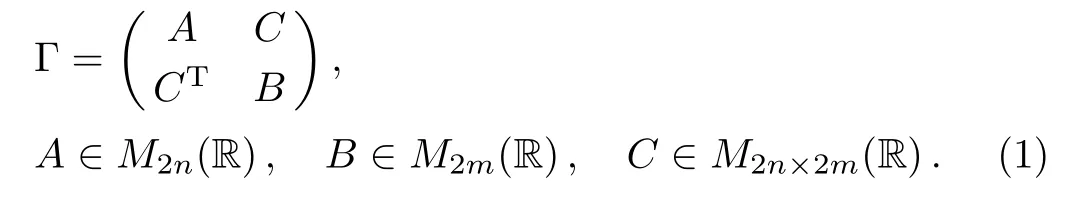
Particularly,if n=m=1,by means of local Gaussian unitary(symplectic at the CM level)operations,Γ has a standard form

Gaussian Unitary TransformationLet Gndenote the set of all n-mode Gaussian unitary operators U,which maps Gaussian states into Gaussian states.By Ref.[27],for any U∈Gn,there exists a symplectic matrixsuch thatwhere mUis a vector of R2n.The above equation induces the transformation of displacement d and CM Γ:Particularly,if U has the formthen it corresponds to a real symplectic matrix,where
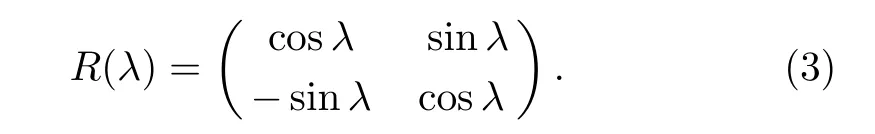
3 Quantum Correlation by Local Gaussian Unitary Operations for Gaussian States
Based on the de finition of D(ρAB,UA),the authors[25]de fined the minimum change induced by local unitary operators as follows:
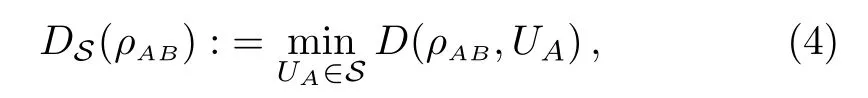
where S is a suitably chosen set of unitary operations.Furthermore,by choosing

where E∈B(HA)is any fixed Gaussian unitary operator withand mE=0,some properties of DS(ρAB)are obtained.
Proposition 1(Ref.[25])DSis locally Gaussian unitary invariant(symplectic invariant at the CM level).
Proposition 2(Ref.[25])For any(n+m)-mode Gaussian state ρAB,the following statements are equivalent.
(i) ρABis a product state if and only if DS(ρAB)=0.
(ii)The operator E in Eq.(5)can be identified with a nontrivial phase transformation∑i.e.,the set S can be written as
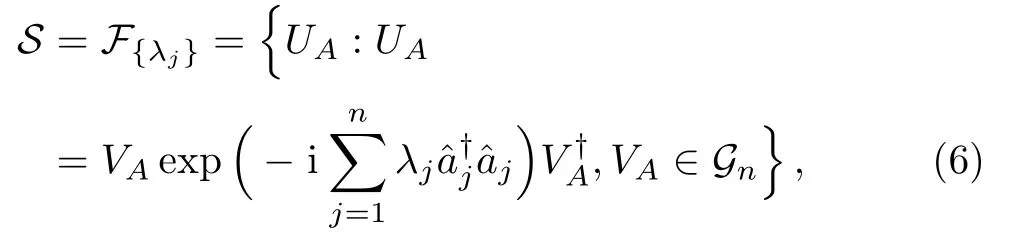
where λjis not integer multiple of 2π,j=1,2,...,n.
Note that Hilbert-Schmidt norm satisfies the three conditions of D(ρAB,UA).In this paper,we will use the Hilbert-Schmidt norm to discuss DS,that is,we de fine

where the minimum is taken over all Gaussian unitary operators UAin S de fined by Eq.(6).
Firstly,we give a formula of DSfor any(n+m)-mode Gaussian states.
Theorem 3For any(n+m)-mode Gaussian state ρABwith CM Γ as in Eq.(1),we have

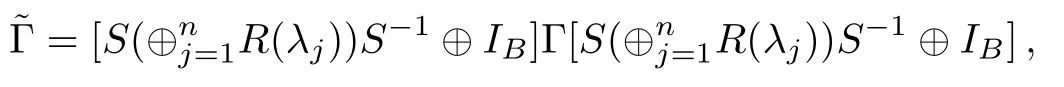
ProofAssume that ρABis any(n+m)-mode Gaussian state with CM Γ.Letwhere UA∈S as in Eq.(6).It is easy to check that the displacement ofis mUAand the CMis
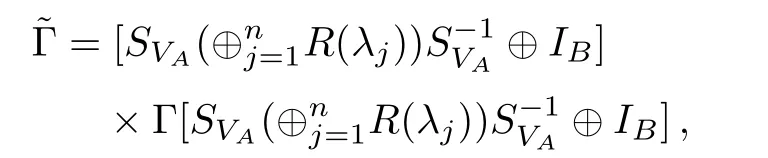
where R(λj)is de fined by Eq.(3),and λjis not integer multiple of 2π(j=1,2,...,n).
Note that,for any two Gaussian states ρ1,ρ2with CMs Γ1,Γ2and displacementsµ1,µ2,respectively,by Ref.[28],we have

where δµ= µ2− µ1.So

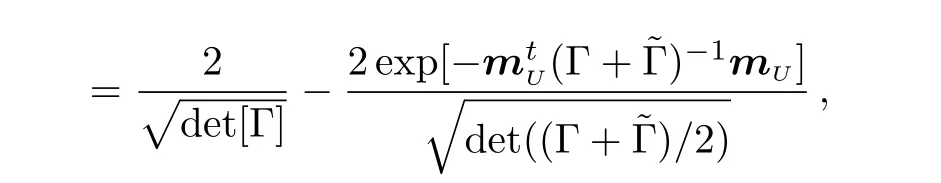

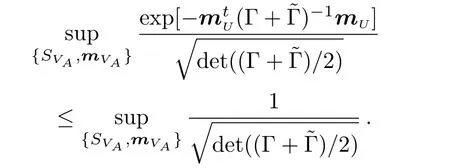
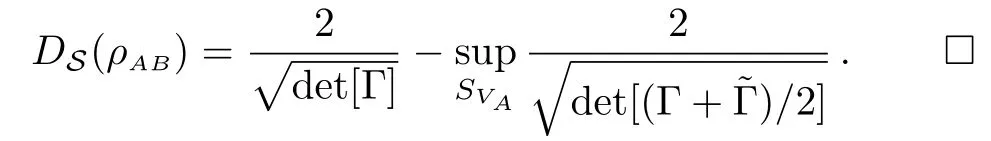
By Theorem 3,for some special class of two-mode Gaussian states,we can get more concrete formulas.
Theorem 4For any(1+1)-mode Gaussian state ρABwith standard CM
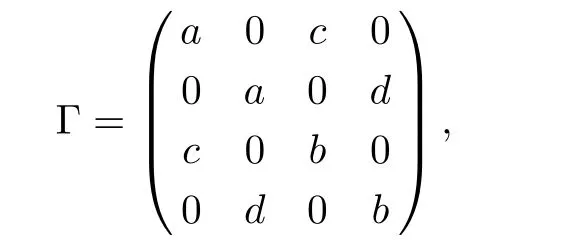
where a,b≥1,c≥0,d=±c and ab−1≥c2,we have
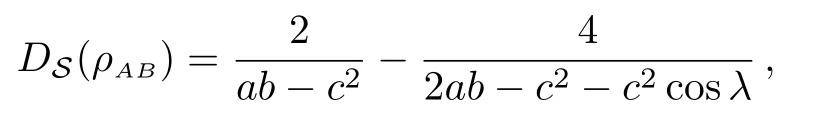
where λ ∈ R not integer multiple of 2π.
ProofBy Ref.[29],any symplectic matrix S∈SP(2,R)has the form S=R(θ)S(x),where

θ∈ [0,2π), x∈ (−∞,+∞).
By Theorem 3,we have
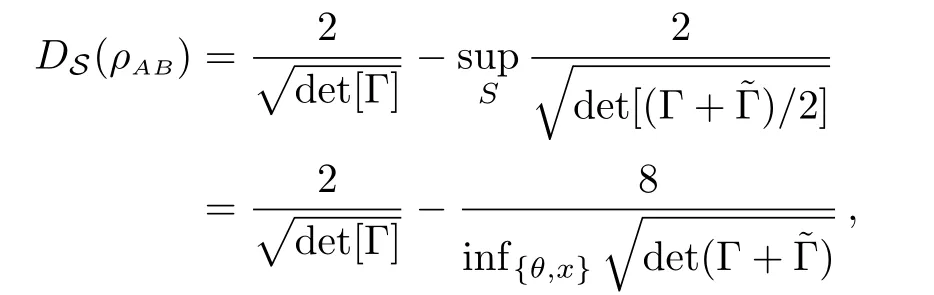
where the supremum is taken over all symplectic matrices
A direct calculation gives
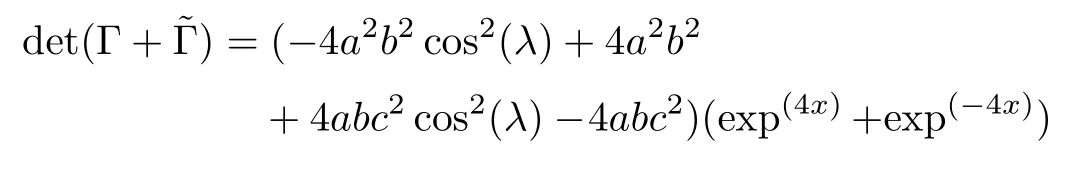

It is easily checked that
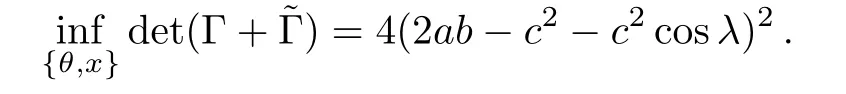
Hence

completing the proof.
4 The Change ofDS(ρAB)after Local Gaussian Channels
Recall that a Gaussian quantum channel is a quantum channel that transforms Gaussian states into Gaussian states.Assume that Φ is a Gaussian channel on nmode Gaussian systems.By Ref.[30],for any n-mode Gaussian state ρ with CM Γ and displacement d, Φ(ρ)has the CM XΓXT+Y and displacement Xd+m,where X and Y are two real 2n×2n matrices with Y symmetric and det(Y)≥(1−det(X))2,and m∈R2nis a vector.Thus Φ can be represented as Φ(X,Y,m).
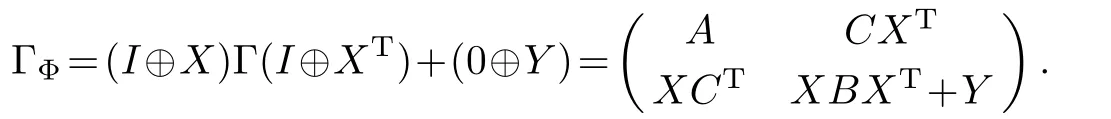
By Theorem 3,one has


By Eqs.(7)–(8),it is difficult to compare DS(ρAB)and DS((I ⊗ Φ)(ρAB))for any Gaussian channel Φ and any Gaussian state ρAB.So we only discuss several special one-mode channels for two-mode squeezed thermal states(STSs)and mixed thermal states(MTSs)here.
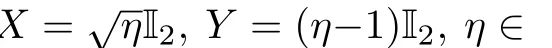
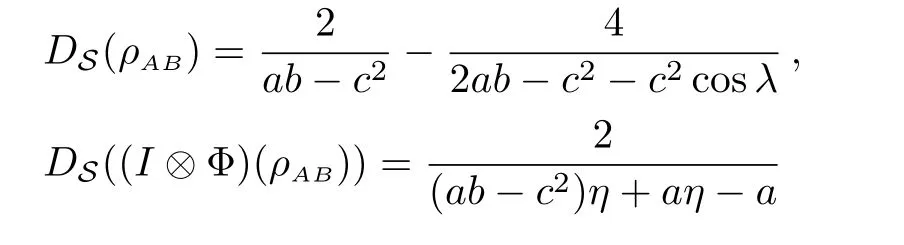

Now,for every λ ∈ (0,2π),de fine a function f(η)with variable η ∈ (1,∞)by

Then the differential function
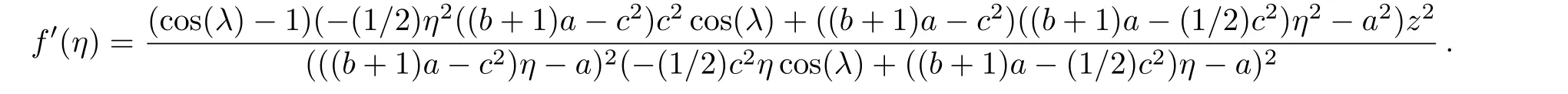
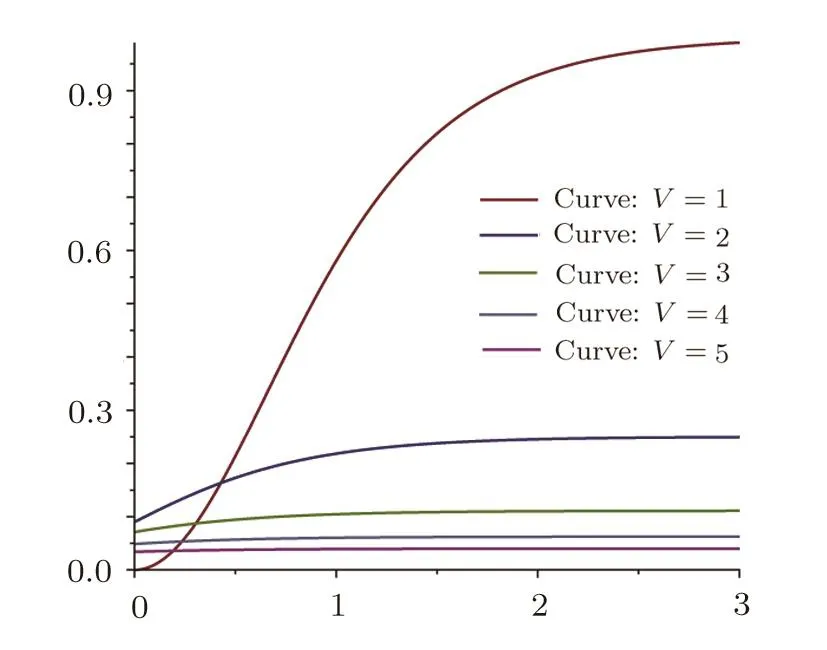
Since ab− c2≥ 1,it is easily checked that f′(η)<0 for all η ≥ 1,which implies that f(η) Fig.1 ρ is any squeezed thermal state and Φ is any local amplification channel.Choose a=b=2k,c=k,k ∈ (0,10),and λ = π. Still,by a similar discussion to that for amplification channels,we find thatif ab−c2≤a≤ab−(1/2)c2−(1/2)c2cosλ. In this section,we will compare DSwith entanglement for symmetric squeezed thermal states(SSTSs). Recall that SSTSs are those Gaussian states whose CMs Γ are parameterized by their symplectic eigenvalues v=v1=v2and r such that where r is the squeezed parameter(Ref.[25]). For any two-mode Gaussian state ρAB,logarithmic negativity in Ref.[32]is de fined by On the other hand,by Theorem 4,we have Fig.2(Color online)x-coordinate denotes the quantity E(ρAB)and y-coordinate denotes the quantity DS(ρAB)for any two-mode SSTS ρAB. The curves stand for DS(ρAB)as functions of E. Figure 2 gives the relation between maxDS(ρAB)and the entanglement measure E.We see from Fig.2 that,for any fixed value E(ρAB)∈ [x0,∞)with 0 In summary,in this paper,we discuss the nonlocality DSinduced by local Gaussian unitary operators with Hilbert-Schmidt norm for any(n+m)-mode Gaussian state.The analytic formulas for two-mode squeezed thermal states and mixed thermal states are obtained.We also compare DS(ρAB)andfor some special Gaussian channels Φ.Finally,the quantity is compared with entanglement in terms of logarithmic negativity. Acknowledgments The authors thank all referees for their many helpful comments.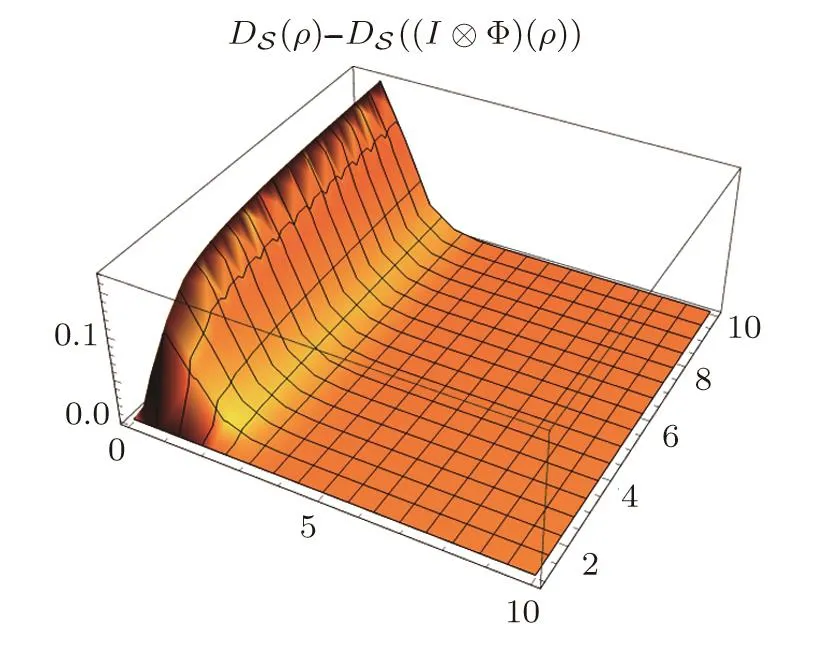

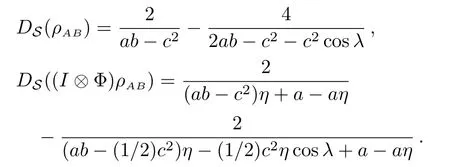
5 Relation BetweenDS(ρAB)and Entanglement

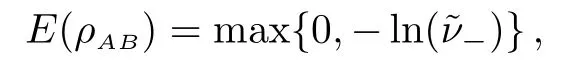
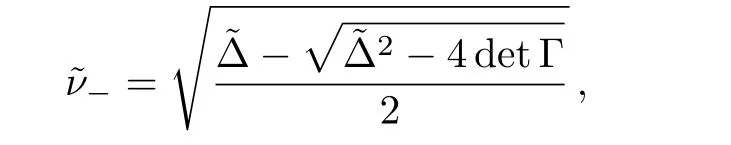
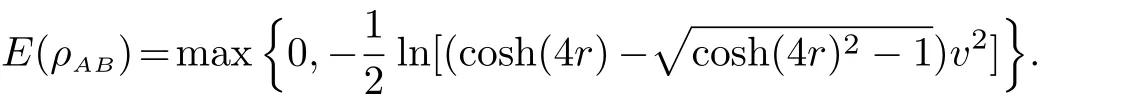
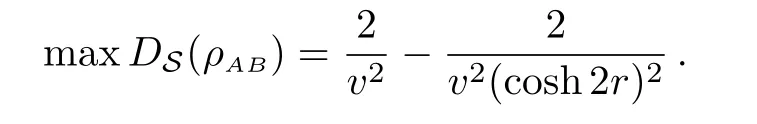
杂志排行
Communications in Theoretical Physics的其它文章
- A Numerical Investigation of Nanocomposite of Copper and Titanium Dioxide in Water Based Fluid Influenced by Instigated Magnetic Region
- Effects of Thermal Radiation on a 3D Sisko Fluid over a Porous Medium Using Cattaneo-Christov Heat Flux Model∗
- Energy Transfer in the Light-Harvesting Complexes of Purple Bacteria∗
- Effect of Critical Beam Radius on Self-focusing of cosh-Gaussian Laser Beams in Collisionless Magnetized Plasma
- Phase Sensitive Photonic Flash∗
- Jeans Instability of Self Gravitating Dust Cloud in Presence of Effective Electrostatic Pressure
