单调测度空间上一般实值可测函数的泛积分
2018-08-02徐鹤萍张承坤李军
徐鹤萍,张承坤,李军
(中国传媒大学理学院,北京 100024)
1 引言
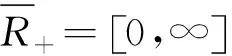
文献[1]中给出了基于普通加法和乘法的一般可测函数的泛积分的定义,在次可加的假定下,讨论了一般可测函数泛积分的线型性。本文将进一步讨论一般实值可测函数泛积分的基本性质,并给出相应的泛积分收敛定理。
2 预备知识
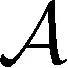
下面我们回顾单调测度和非负可测函数的泛积分的定义。
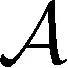
(1)μ(φ)=0且μ(X)>0;
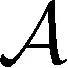
当μ是单调测度时,(X,A,μ)称为单调测度空间。

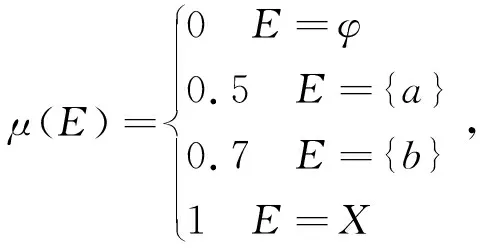

取A={a},B={b},则
μ(A)+μ(B)=1.2≠1=μ(A∪B)=μ(X)。
显然,单调测度μ不具有可加性。
一个集函数μ称为
μ(A∪B)≤μ(A)+μ(B)。
下面我们回顾非负可测函数的泛积分的定义。
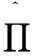
例2.2 在例2.1定义的单调测度空间中,我们设
可得



由此可知

所以泛积分不具有线性性。

非负可测函数泛积分有以下基本性质(可参见文献[10])。



一般地,基于单调测度的泛积分不具有线型。然而当单调测度是次可加的,则对应的泛积分具有线型性,即文献[1]中证明了以下结论:

3 一般实值可测函数的泛积分
本节中我们讨论一般实值可测函数的泛积分。

f=f+-f-,
其中,f+和f-分别表示f的正部和负部,即

文献[1]中引入了一般实值可测函数的泛积分的定义,我们陈述如下:




当f是非负可测函数时,定义3.1中泛积分的定义与定义2.1一致.因此,一般可测函数泛积分的定义是非负可测函数泛积分定义的推广。





5)若f是可积的,则f是可积的。
证明:由文献[10]中非负可测函数的泛积分性质,1),2)显然成立。
3)对非负函数的泛积分有

当c≥0时,

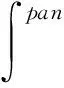
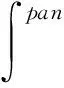
当c<0时,

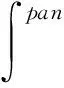
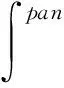
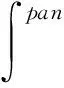
4)由f≤g可知,f+(x)≤g+(x),f-(x)≥g-(x),由性质2.1中的3)可得,

即

5)由于f+≤f且f-≤f,根据性质2.1(3)和f的可积性可知,
f+可积且f-也可积,因此可得f是可积的(在定义3.1的意义下)。
性质证毕。
注1:在经典Lebesgue积分理论中,f的可积性与f的可积性是等价的。
一般地,以上性质(5)的逆命题是不成立的,即由f的泛可积性推不出f的泛可积性。

由此可知f是泛可积的,而f却不是泛可积的:

性质3.2 设μ是次可加的。若f是泛可积的,则f是可积的。
证明:由于f是可积的,且μ是次可加的,由定理2.1[1]可得:

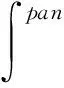
我们知道,一般地,基于单调测度的泛积分不具有线性性,当考虑的单调测度是次可加时,那么相应的泛积分具有线性性。文献[1]中得到了以下结果:
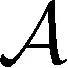

证明:由于μ是次可加的,f和g均可积,故f和g均可积;
由于f+g≤f+g,故f+g可积;

从而,

由非负可测函数的泛积分可得,
由此得


证明:由f=f++f-及非负可测函数的泛积分具有线性可知,

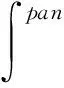
且
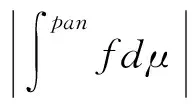
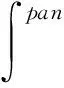
从而
以下我们陈述泛积分的Levi单调收敛定理和Fatou引理,证明与Lebesgue积分的证明一致(参见文献[13])。

定理3.4(Fatou引理)设fn:A→0,∞是非负可测函数列,则
以下我们给出泛积分的一类控制收敛定理:

2)存在A上的泛可积函数g,使得对每一n≥1,在A上几乎处处有fn(x)≤g(x),
则f和fn都在A上泛可积,并且
证明:由fn(x)≤g(x),分以下两种情况讨论:
1)fn(x)≤g(x);
2)-fn(x)≤g(x)。
对第一种情况可得:g(x)-fn(x)≥0,
由Fatou引理得
由μ的次可加性可知,泛积分具有线性性,因此,
由Levi单调收敛定理,
即
对第二种情况可得:g(x)+fn(x)≥0,
由Fatou引理得
由μ的次可加性可知,泛积分具有线性,因此,
由Levi单调收敛定理,
综合一二两种情况即得
定理证毕。

根据外侧度的性质,本文中的性质2.1、定理2.1、性质3.1、性质3.2、定理3.1、定理3.2、定理3.3、定理3.4、定理3.5对基于外侧度的泛积分仍然成立。特别地,我们强调基于外侧度的泛积分具有线性性。
