理想间隙波导结构的理论分析
2018-08-02肖怀宝方超逯贵祯
肖怀宝,方超,逯贵祯
(中国传媒大学,信息工程学院,北京 100024)
1 引言
间隙波导是当前国际学术界在毫米波和亚毫米波领域中提出的一种新的传输线结构,该结构可以低损耗传输TEM波。从公开发表的文献来看,关于间隙波导技术的研究主要还是以数值仿真分析为主,由于其结构的复杂性,数值计算对计算机性能要求也较高。从2009年开始,该领域研究受到了广泛的关注,P S Kildal及其团队研究了该结构的应用领域,如在毫米波和亚毫米波的低损耗传输特性[1-3]、在微带电路中的封装和隔离技术[4] [5]、高Q值的微带线滤波技术[6]等;间隙波导结构的实现技术[7-9]、间隙波导的分析方法[10][11]及其特性参数等[12]。此外,其他国家的研究人员也开始关注间隙波导的相关研究领域[13][14]。其中,P S Kildal在论文[10]中对间隙波导技术进行了阶段性的论述,并对其间电磁波的波矢量进行了比较详细的理论分析,但遗憾的是,对于间隙波导中场的解析表示式,用了假定表达式。国内对间隙波导的研究相对比较晚,2014年,逯贵祯等对基于金属条带缝隙的波导结构进行了仿真研究[15],2016年,朱明等[16]通过仿真优化间隙波导结构参数,根据仿真参数加工出了实际的间隙波导,把实物测量结果与仿真结果进行了对比,验证了该结构在波的传输方面的特殊性,同时通过色散图法对间隙波导结构的传输特性进行了分析[17]。方超将间隙波导结构运用在缝隙微带天线的馈电上,改善了天线的性能,减小了天线的背向辐射[18]。本文将对理想磁导体边界的间隙波导结构进行理论分析,导出其解析表达式,并用数值解与解析解的对比来验证理论分析的正确性。
2 均匀导波系统分析的理论基础
假设均匀导波系统中场沿+z方向传播,频率为ω,则场的表达式为:
(1)
必须满足麦克斯韦方程组:

(2)
上式在直角坐标中展开,得:
(3)
求解方程(3)式,可以用纵向场(Ez,Hz)来表示横向场(Ex,Ey,Hx,Hy)并令:
k2=ω2με
(4)
则有:
(5)
由上式可以看出,对于均匀导波系统,为了求解方便,可以先求出纵向场的解,然后利用式(5)求得横向场,从而减少计算量。对于正弦电磁波,场应满足亥姆霍兹波动方程:
(6)
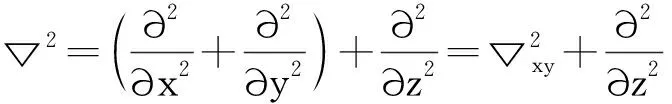
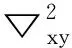
(7)
因此,式(6)可改写为:
(8)
此即导波系统中电场和磁场应满足的微分方程。对于确定的导波装置,可由给定的边界条件,通过求解上式,得到纵向场分量(Ez,Hz),再通过式(5)求得其余横向分量(Ex,Ey,Hx,Hy)。
3 基于PMC结构的间隙波导系统场特性分析
图1是间隙波导的一种实现结构示意图,高度为λ/4的pins组成了高阻区,使得电磁波只能在2a×b区域中传播,为了求解该区域的场的解析解,对高阻区用理想磁导体(Perfectly Magnetic Conducting,PMC)边界条件来替代。其简化的基于PMC边界的间隙波导截面示意图如图2所示。为了说明方便,把分析区域分为三部分,分别为标为I区、II区和III区,其中I区为2a×b区域、II区和III区为d×b区域。边界如图所标注。由于在这种导波系统结构中,理论上只能传输TEM波(严格地讲是准TEM波),因此,设波的传播方向为+z方向,电场为y方向,磁场为x方向。
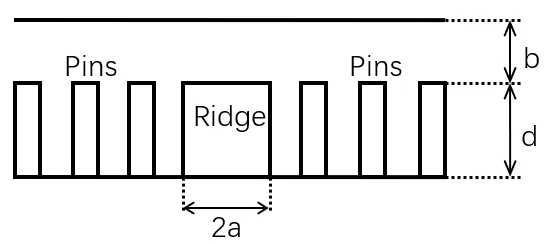
图1 间隙波导结构
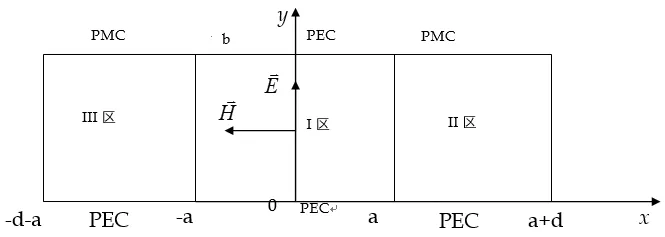
图2 基于PMC的间隙波导结构示意图
由于该导波系统传输的是TEM波,在传播方向上不存在场分量,即Ez=0,Hz=0因此,由式(5)易知,要使场的横向分量不为0,则有:
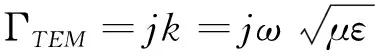
(9)
把k2+Γ2=0代入公式(8)得TEM波的场方程:
(10)
同理可得:
(11)
由式(10)和式(11)可知,间隙波导中的场与无源区静态场所满足的场方程相同,因此可以通过求解电势φ来间接求解电场。
3.1 电势满足的方程及其解
由前面分析可知,间隙波导中的场与无源区静态场所满足的场方程相同,因此其电势φ满足的方程为拉普拉斯方程,即:
(12)
根据分离变量法,设φ=X(x)Y(y),则式(12)可变换为:
(13)
其中λ为本征值。
根据对称性,II区和III区场应具有相同的形式,因此,下面的讨论中我们只关注I区和II区场的求解。
3.1.1 区场分析
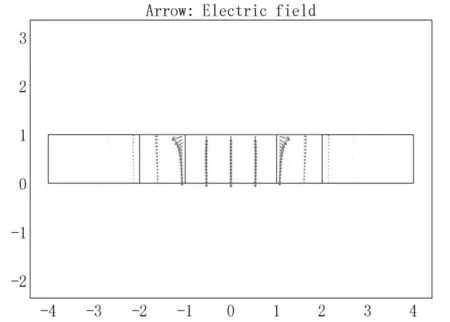
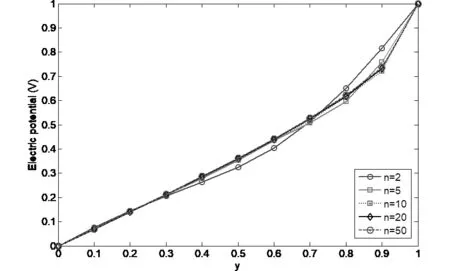
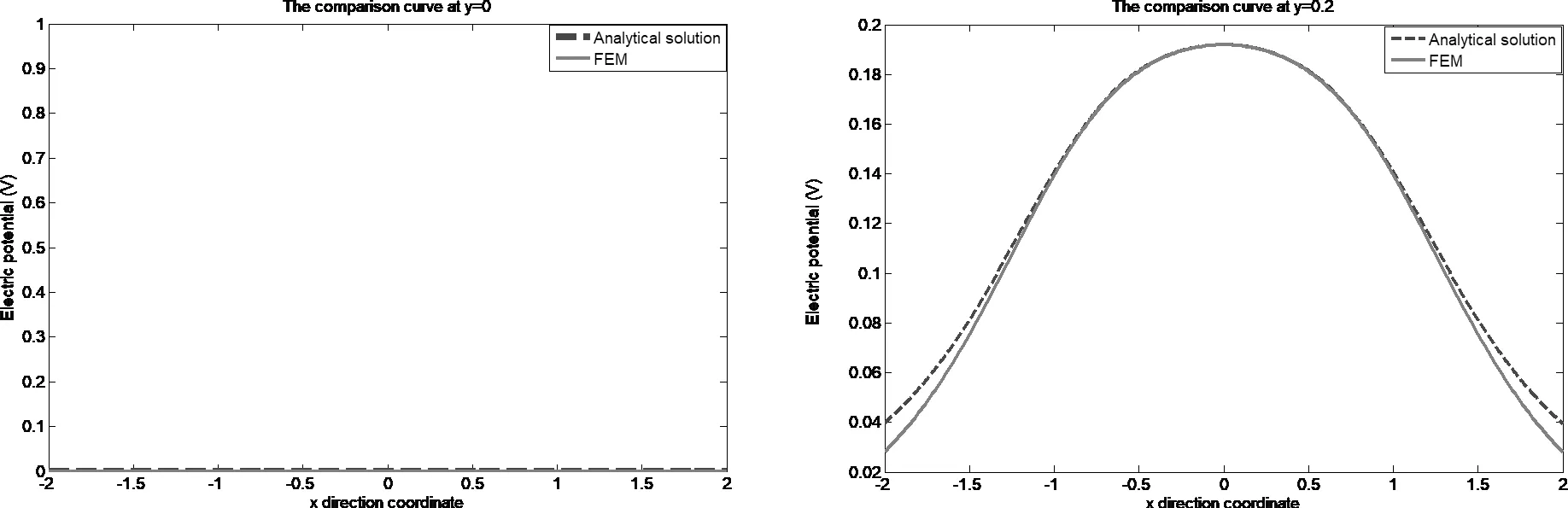
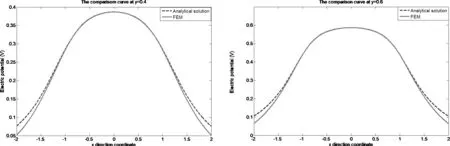
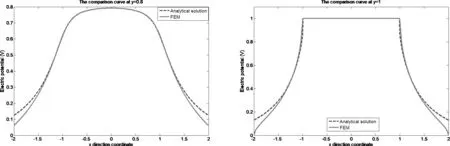
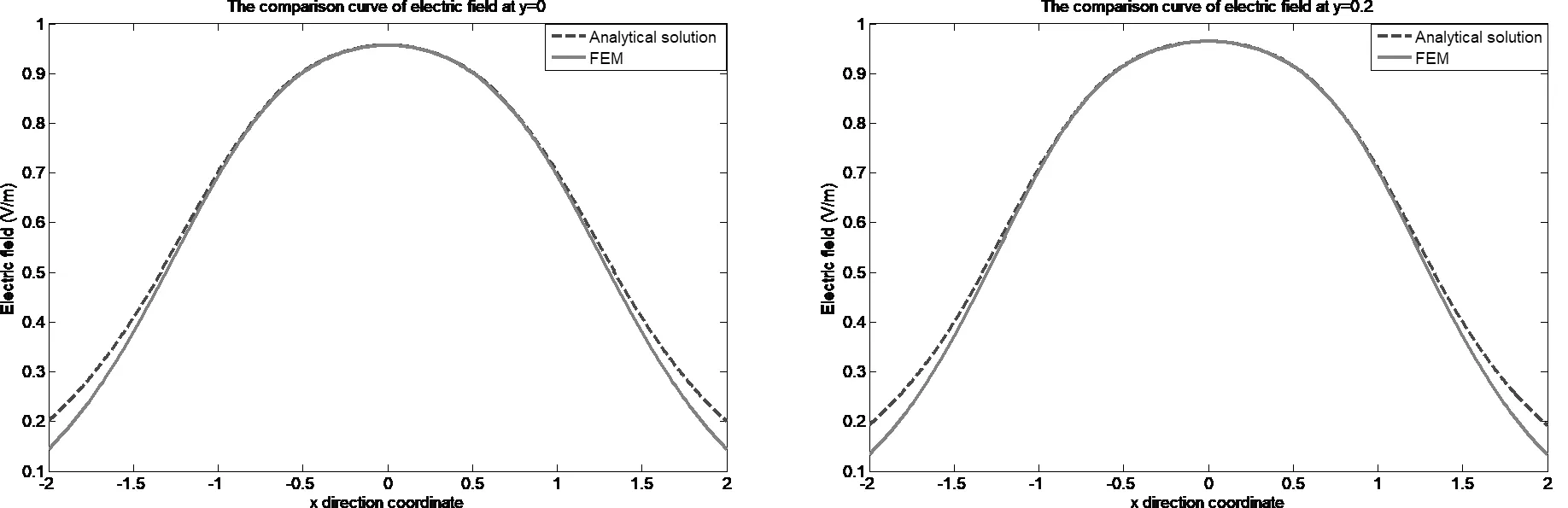
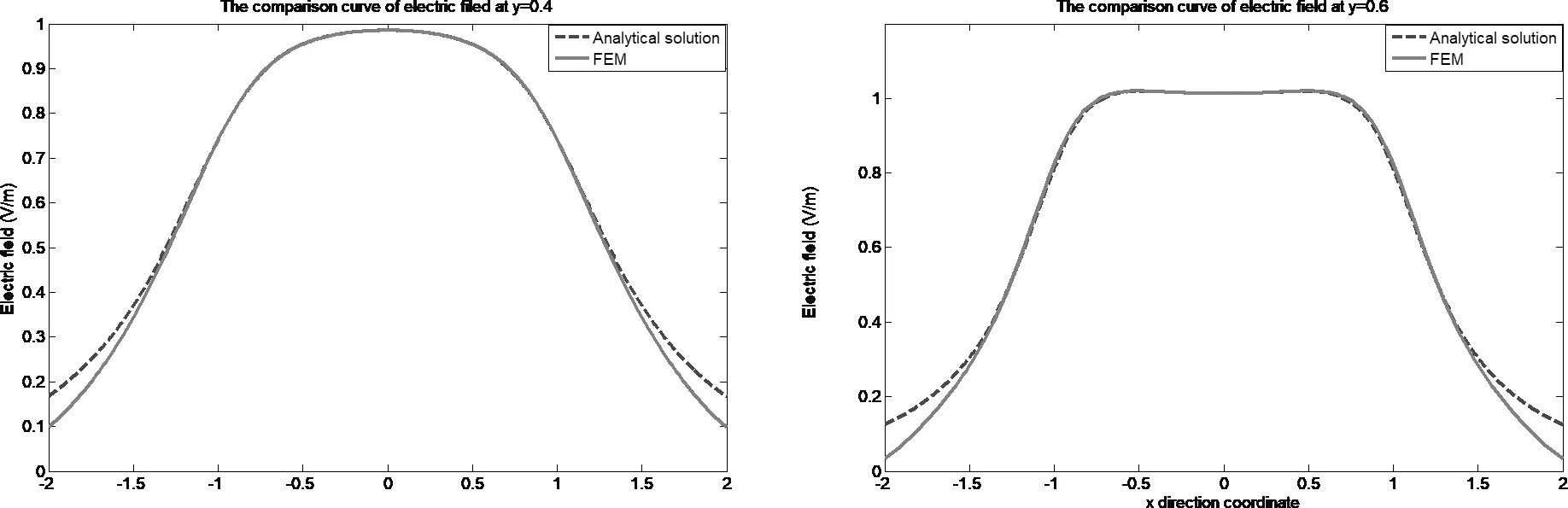
根据间隙波导的结构特点可知,I区场(-a 由式(13)易知,λ=0满足方程,此时的解可写成: (14) 其中,dx,dy是待定常数,则: φ10=CxCyY=Cy (15) 是电势φ1的一个解(主模)。不失一般性,设边界条件为: (16a) 在考虑边界条件后,式(15)可写为: (17) 则在λ≠0时,边界条件为: (16b) 再考虑到对称性,解的形式可表示如下: (18) (19) 为了跟Ⅱ区场一致,求和从n=0开始,并不影响电势值。 3.1.2 Ⅱ区场分析 Ⅱ区场(a (20) Ⅱ区的边界条件为: (21) (22) 3.1.3 Ⅰ区和Ⅱ区场的连续性分析 公式(19)和式都分别含有未知系数,为了确定这些系数,我们根据I区和II区场的连续性条件来进行分析。在两求解区的分界面(x=a)上,场应满足连续性条件,即φ1(a,y)=φ2(a,y),得: (23) 同时,电势还满足法向导数连续,即: (24) 由式(23)和式(24)组成2n个方程可以确定cn和dn的值。 为了验证理论的正确性,我们利用COMSOL仿真软件对基于PMC结构的间隙波导进行了数值仿真分析,建模时取a=b=1(归一化长度),图3是有限元计算结果的电势分布图,图4是有限元数值计算的电场示意图,由这两张图可以看出,电磁波基本上被局限于I区进行传播,在Ⅱ区和Ⅲ,场急剧衰减。在理论计算时,由于场的表达式是无穷级数形式,因此在实际画图时,我们只取了前10项,事实上,所得的结论对n>2的项数不是很敏感,图5所示是取不同项数(n不同)时,理论计算的电势曲线,由图可知,n>2时,电势的理论计算曲线几乎是重合的。图6所示为电势理论值随高度y的变化曲线,理想情况下,传播的是TEM波,因此电势理论值随y的变化应该是一条直线,但在实际情况下,由式(19)可知,电势表达式是线性函数y/b与无穷级数的代数和,因而电势与y的关系不再是条直线,而是略有弯曲。 图3 有限元计算的电势分布图 图4 有限元计算的电场示意图 图5 电势理论值随n的变化曲线(y=0.9b) 图6 取不同项数时电势理论值随y的变化曲线(x=a) 电势的有限元计算结果与解析解的结果对比如图7所示,由这些对比图可以看出,在I区(-a y=0时 y=0.2b时 y=0.4b时 y=0.6b时 y=0.8b时 y=b时图7 电势理论结果与仿真结果对比曲线 与静态场相同,由电势φ得到I区的电场表达式为: (25) 由上式可以看出,I区电场具有x分量,但由于sinh(x)是关于x的奇函数,根据对称性,在I区中矢量和为零,所以总场只有y分量,与开始的TEM波假设是一致的。但在x=±a的边界附近处,总场将是I区电场和II区电场的迭加。 同理可得II区场的表达式为: (26) 理论计算值与仿真值y分量绝对值的对比如图8所示,实际上我们更关心的是I区电场。 y=0时 y=0.2b时 y=0.4时 y=0.6b时 y=0.8b时 y=b时图8 电场理论结果与仿真结果对比曲线 (27) 其中Z0是真空中的波阻抗。则: (28) (29) 故: (30) 因为dn很小,因此: (31) 所以有: (32) 该结论与文献的结论相同。 本文对均匀导波系统的一般理论进行了阐述,得到分析导波系统的一般方程,然后对基于PMC边界的间隙波导进行了理论分析,发现其场方程与静态场方程具有相同的形式,因此可以在给定的PMC边界条件下,通过求解电势所满足的方程来间接求解场。利用分离变量法得到了电势解析解,通过电场与电势的梯度关系得到电场的解析解。为了验证解析解,利用有限元仿真软件对基于PMC结构的间隙波导模型进行数值分析,然后把数值解与解析解进行对比,对比的结果表明解析解很好的反映了间隙波导的场结构。运用得到的解析解推导出间隙波导的特性阻抗,特性阻抗的结论与文献的结论相同,进一步证明了解析解的正确性。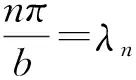
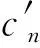
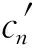


3.2 电场的解及其仿真分析
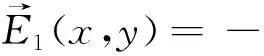

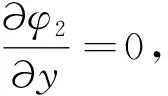

3.3 特性阻抗
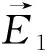
4 结论
