被施了魔法的娃娃 （四）——奇妙的密铺

○张丽琴

由于玛丽娜创作的每个娃娃背后都有故事，给人们带来艺术创作上的启发和思考，所以说这是一项跨越层次，跨越多个艺术领域的灵感激荡，是一项非常多元化、令人迷醉的触觉体验以及油然而生的关于生命的创造。在这个过程中，有绘画、雕刻、工业设计、模具制作、金工、时装和珠宝设计，一切的一切，她能想象的，她需要的，都在这个孕育的过程中得到丰盛的满足。

上图中这个戴王冠的精致人偶，皮肤白皙光滑，娇小脆弱，似乎风不可吹。她表情抑郁，像是含泪哀诉。

玛丽娜精心设计的娃娃衣着上的图案美轮美奂，夺人眼目。其中许多图案是密铺的。密铺是什么？所谓“密铺”，就是指任何一种图形，如果能既无空隙又不重叠地铺在平面上，这种铺法就叫做“密铺”。可以进行密铺的图形叫做密铺图形。用形状、大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙、不重叠地铺成一片，这就是平面图形的密铺，又称做平面图形的镶嵌。

哪些平面图形可以密铺呢？由密铺的定义不难看出：密铺时，几个图形会拼在一个共同的点上，这个点叫作公共顶点。只要图形的角在公共顶点上角度之和是360°，这个图形就能密铺。所有三角形与四边形均可以单独密铺，正六边形也可以单独密铺。

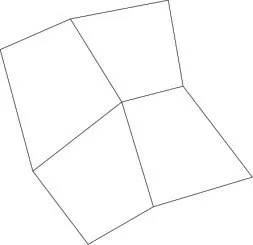
而正五边形却不可以。原因何在？由下图不难看出：因为正五边形的每个内角都是108°，而360不是108的整数倍,在每个拼接点处的内角不能保证没空隙或重叠现象。同样，圆形也不能密铺。

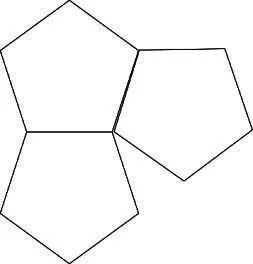
下图是设计师密铺出的美丽图案：

自然界也存在着大量密铺呢！

看来，密铺为我们的生活和艺术创造呈现了色彩斑斓的美！就连蜜蜂都会选择正六边形作为蜂巢的形状，科学家们经过很多年的计算证明，用等量的原料，蜂房做成正六边形能使蜂巢具有最大的容积，因此能容纳最大数目的蜜蜂。

密铺的历史源远流长！1619年，数学家奇柏第一个利用正多边形铺嵌平面。1891年，苏联物理学家费德洛夫发现了十七种不同的铺嵌平面图案。1924年，数学家波利亚和尼格利重新发现这个事实。最有趣的是1936年荷兰艺术家埃舍尔偶然到西班牙的格兰拿大旅行，在参观建于十四世纪的阿罕伯拉宫时，发现宫内的地板、天花板和墙壁满是密铺图案的装饰。他因而得到启发，创造了无数的艺术作品，给人留下深刻印象，更让人对数学有了新的认识。

看来，做生活的有心人，将数学、艺术有效结合，将创造出更多精彩！