基于静力试验的连续小箱梁损伤识别方法

渠广镇

(山东省交通科学研究院，山东 济南 250014)

0 引 言

预应力混凝土装配式小箱梁具有较高的抗弯刚度、抗扭刚度、施工便捷性和适用性，故在国内得到广泛应用。然而，由于施工原因或者养护不合理，导致结构刚度不足，后期运营时可能致使混凝土箱梁产生较大面积开裂。因此，对于运营中预应力混凝土小箱梁，如何准确地识别出损伤的梁板或者定量判断梁板刚度的降低程度，对后期加固较为重要。

相关学者对此也进行了大量研究，如向天宇等通过静力试验，应用有限元模型修正技术进行结构损伤识别[1]；徐向锋等对箱梁进行破坏性试验，建立了裂缝指标CD参数与损伤因子的关系，提出了开裂后箱梁刚度分布计算方法[2]；赵煜等通过建立基于主要裂缝统计特征参数的开裂预应力混凝土箱梁损伤计算模型，进行损伤识别方法研究[3]。

基于模型修正的损伤识别一般是将结构的损伤表示为单元刚度的损伤，它需要2个模型修正过程：修正模型的不确定因素， 包括模型结构误差、模型阶次误差和模型参数误差， 建立完好结构的基准有限元模型；利用损伤状态的测量响应，修正参考模型，并通过修正后模型与基准模型的比较进行损伤识别[4-5]。本文通过对1座运营3年后存在大量裂缝的连续小箱梁进行静力试验，来定量判断其刚度损伤状况。

1 工程概况

某装配式预应力混凝土连续小箱梁结构型式为20 m×30 m，四跨一联，单幅横向布设4片梁，如图1所示。桥面铺装为10 cm厚C50混凝土桥面现浇层和10 cm厚沥青混凝土。该桥于2014年建成通车，在近2年的桥梁普查中发现，该桥上部结构主要存在箱梁底板沿波纹管纵向断续裂缝、底板跨中横向裂缝、腹板水平断续裂缝、腹板斜裂缝等病害。检测裂缝宽度范围为0.05～0.30 mm，部分裂缝超出规范限值0.2 mm。在检测的80片小箱梁中，33片箱梁底板存在53条断续纵向裂缝；13片箱梁腹板存在16条断续水平裂缝；41片箱梁翼板存在52条纵向裂缝；4片箱梁底板存在7条横向裂缝；6片箱梁腹板存在10条斜裂缝。主要裂缝分布见图2。

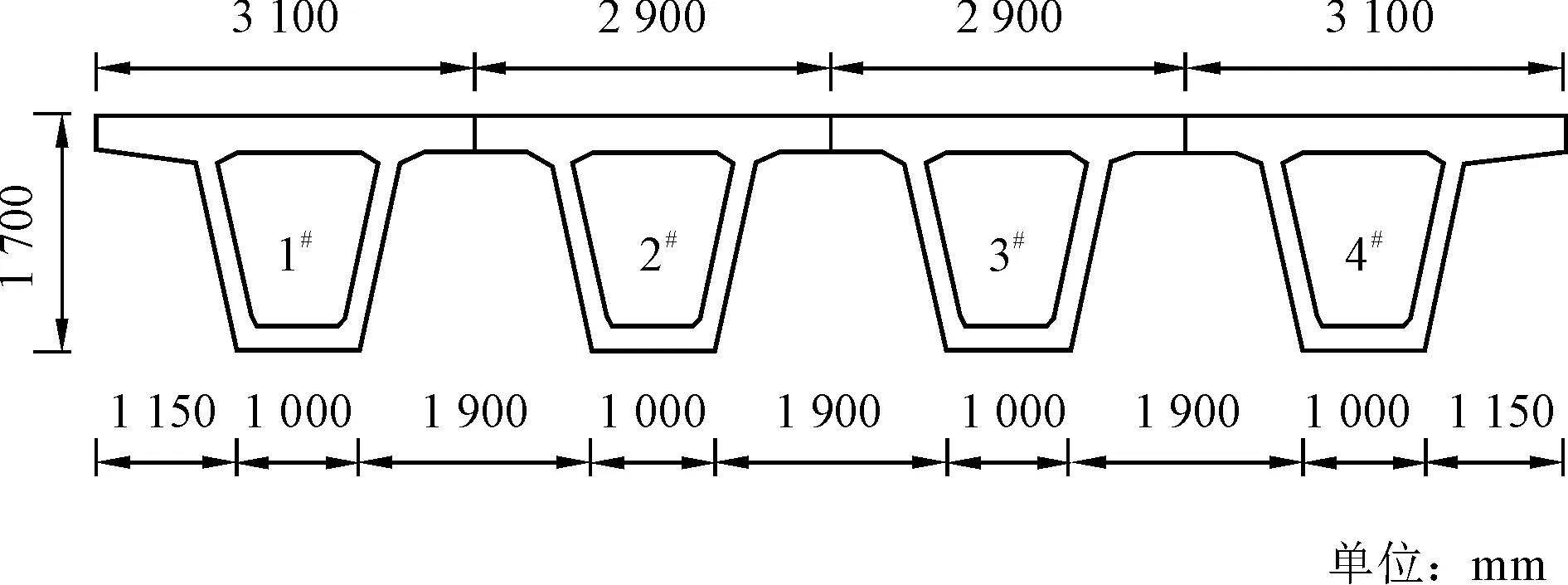
图1 小箱梁横截面

图2 预应力小箱梁主要裂缝分布

对本桥交通量进行实测归类统计发现：在不考虑小车影响时，本桥通行六轴车比重为28%，五轴车比重为10%，四轴车比重为15%，三轴车比重为13%，两轴客货车比重为34%。其中大型及以上车型(三轴及以上货车)约占66%。各轴车型均存在不同程度的超载现象，其中两轴车超载率为5%，三轴车超载率为6%，四轴车超载率为12%，五轴车超载率为50%，六轴以上车超载率为71%，超载大型货车的最大实载约为限载值的1.3倍。

2 静力试验

2.1 数值模拟

为使测试断面荷载效率系数η达到0.95以上，通过Midas/Civil软件用梁格法建立初始状态模型进行计算，初始状态参数见表1。梁格法的基本原理是将桥梁上部结构用一个等效梁格来模拟，用多条纵向单元来模拟多片主梁，把分散在主梁每一区段内的弯曲刚度和抗扭刚度集中在最近的等效梁格内，梁板的纵向刚度集中于纵向梁内，横向刚度集中于横向梁内[6-8]。基于上述原则，建模时小箱梁纵向1 m一个单元，每个节点横向用虚拟横梁连接，解除梁端约束。虚拟横梁只有刚度没有质量。计算时考虑6 cm的铺装层参与受力[9]，分析模型见图3。

表1 设计参数初始值

图3 梁格模型

2.2 试验工况

本桥主要的测试断面为第1跨14 m处断面(A断面)、第2跨跨中截面(B断面)及1#墩顶边跨侧1 m处断面(C断面)，如图4所示。在A、B断面底部分别设置位移计和应变片，在C断面底面设置应变片[10]。本桥静力测试共设置以下5个工况试验。

(1)工况1、工况2：第1跨A断面满载下最大正弯矩效应的对称、偏载试验。

图4 测试断面

图5 车辆纵向布置

(2)工况3、工况4：第2跨B断面满载下最大正弯矩效应的对称、偏载试验。

(3)工况5：1#墩顶处C断面满载下最大负弯矩的对称试验。

本桥采用6辆三轴320 kN自卸汽车“尾对尾”加载方式，该车前轴与中轴间距3.8 m，中轴和后轴间距1.4 m，前轴轴重60 kN，中轴和后轴轴重260 kN。车辆布置见图5。

2.3 试验结果

本文对挠度测试数据进行分析，工况1～4测试断面各梁的挠度校验系数见表2和图6。其中，第1跨的各梁挠度校验系数均小于1，而第2跨的部分梁板挠度校验系数出现大于1的情况，同一片梁板的校验系数在对称加载和偏载情况下基本一致。

表2 各工况满载下挠度校验系数

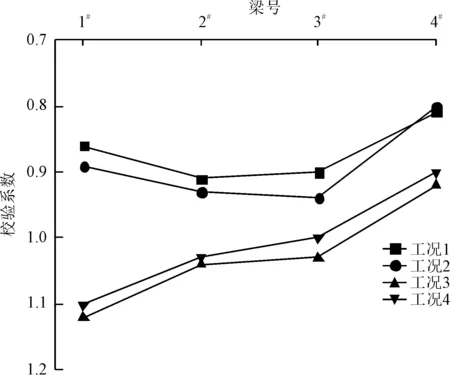
图6 各工况下各片小箱梁挠度校验系数

3 修正参数的选择及设计参数灵敏度分析

在修正过程中，设计变量的选择至关重要。在大跨度桥梁模型参数修正过程中，特征值灵敏度分析是一个选择待修正结构参数的关键环节。在对后期带缺陷的桥梁模型进行修正时，因为出现损伤的未知性，需要对每个单元结构都确定识别参数，如单元刚度衰减系数、单元抗弯刚度以及裂缝的深度、宽度等，这样会导致要修正的参数向量阶数非常大，因此合理选择待修正参数非常关键。

一般有2种方法来解决这个问题。一种是最优子空间方法：先建立参数化的有限元模型，并使得可能的损伤模式都可用这些参数值的组合来表示，然后在有限数量的参数中寻找对测量数据的最优拟合。另一种是统计方法：穷举结构可能的损伤机理和位置，预测损伤导致结构响应的变化，并与测量响应比较，最后选择最可能的损伤模式[11-13]。

本桥钢筋和钢绞线的材料参数已比较明确，而混凝土的材料参数受施工因素的影响，与设计值存在偏差，故仅取混凝土弹性模量、密度、泊松比等参数进行灵敏度分析[14-16]。

目标函数对设计变量的灵敏度可用以下方法确定。

(1)

通过对设计参数进行灵敏度分析，得到小箱梁模型中设计参数变化为±1%，目标函数对于设计参数的绝对灵敏度见图7。

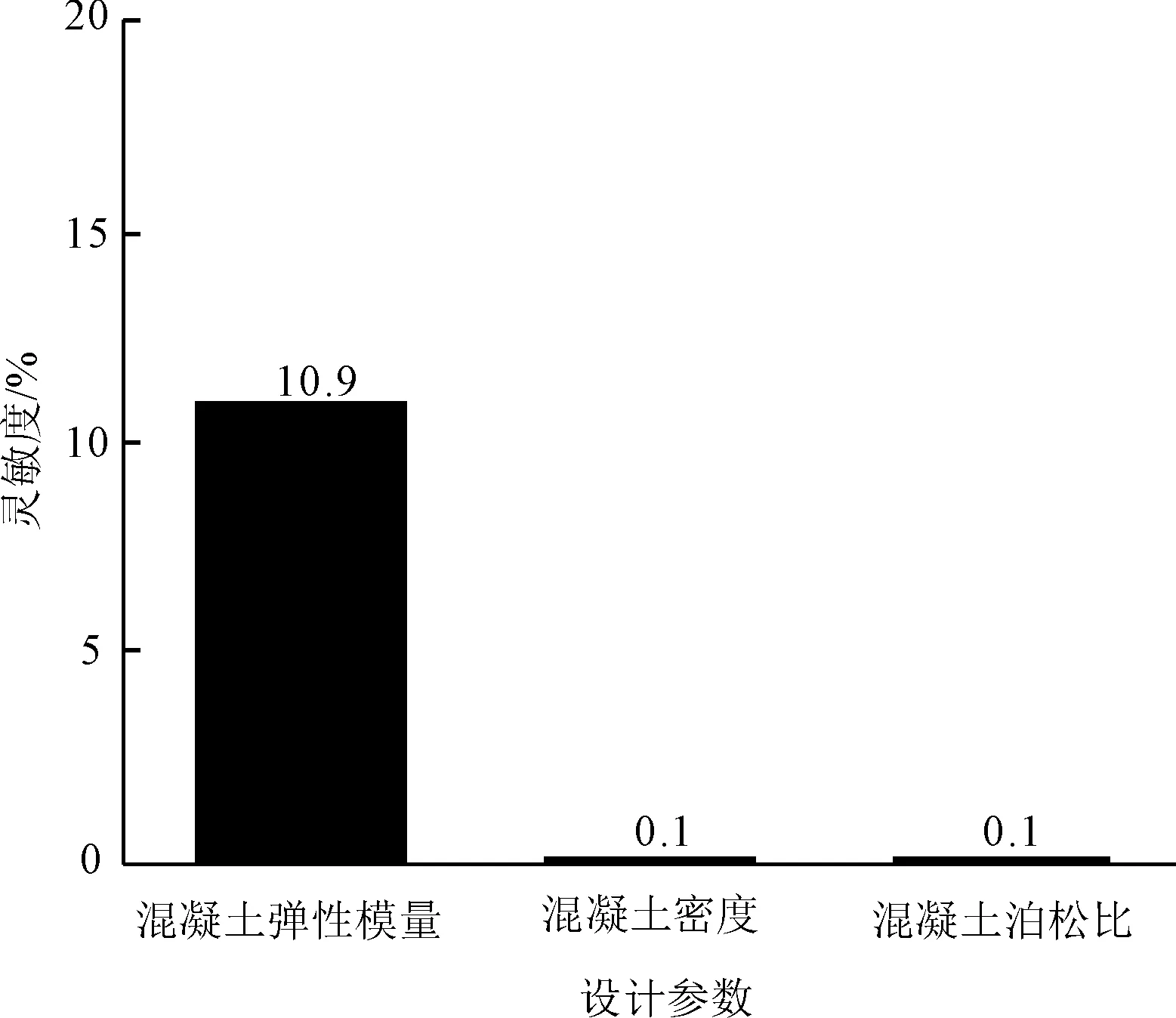
图7 小箱梁目标函数对设计参数的灵敏度

由图7可见：静载挠度计算结果对混凝土弹性模量的变化比较敏感，混凝土的密度、泊松比对挠度的计算结果基本没有影响。故将混凝土的弹性模量选择为修正参数。

4 有限元模型修正

首先分析单片箱梁刚度损伤对结构的影响，进而分析多片箱梁刚度变化的影响，最终定量识别全桥刚度状态。结构损伤后待修正的结构模型特性为主梁的抗弯刚度，通过修正主梁的弹性模量来模拟结构损伤。

E=E0(1-αE)

(2)

式中:E和E0分别为修正后有限元模型弹性模量和初始有限元模型弹性模量，E0=3.45×104MPa；αE为弹性模量的修正系数。

4.1 单片梁弹性模量变化

通过1#、2#梁弹性模量的修正系数αE的改变，可得到αE=0、αE=20%、αE=40%三种模型，3种加载工况下的主梁跨中挠度理论值变化见图8、9。由图8、9可知，单片梁的弹性模量修正对本片梁影响最大，每一模型之间本片梁的挠度变化在10%左右，而其他梁的变化在5%以内。

图8 1#梁弹性模量变化引起的全桥挠度变化

图9 2#梁弹性模量变化引起的全桥挠度变化

4.2 多片梁弹性模量变化

根据工况3跨中实测挠度数据与初始状态理论计算数据比较发现，1#梁和4#梁的挠度相差较大，因此1#梁弹性模量的修正系数αE分别取20%和40%，而4#梁挠度值较初始状态小，因此αE取-20%和-40%，2#、3#梁取初始状态模量，依据水平正交表得出4种模型，见表3。4种模型在试验荷载作用下的跨中竖向挠度计算值和实测值的对比见图10。

从图10可以看出，实测挠度值位于模型1和模型4计算值之间，因此使1#梁弹性模量折减30%、4#梁弹性模量增加30%后，其余梁取初始状态模量，并进行修正后，跨中挠度计算值和实测值吻合，见表4。

表3 正交法计算模型

图10 初次修正后挠度计算值与实测值比较

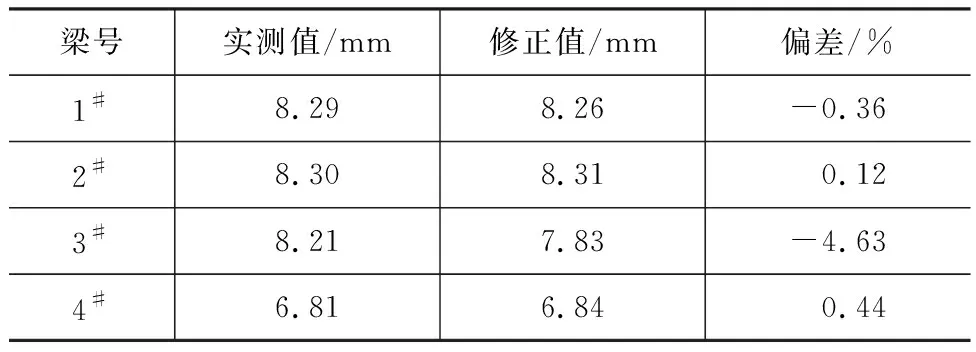
表4 二次修正后挠度计算值与实测值比较

通过静载试验进行全桥刚度损伤识别，识别后的主梁刚度修正系数如图11所示，可知识别后的挠度曲线与实测值比较吻合。

图11 各片梁较原始状态识别修正值

5 结 语

(1)用梁格法建立本桥的有限元模型，各片小箱梁满载作用下的对称和偏载挠度校验系数基本相当。选取其中挠度校验系数较大的一跨进行分析，经过2次模型参数修正，可以对带损伤桥梁结构进行定量识别，经过损伤修正后的计算挠度值和实测值相差5%以内。

(2)结构损伤识别结果显示，最内侧一片小箱梁刚度损伤30%左右，因此可以解释梁板结构出现开裂且裂缝逐年扩展的原因。

(3)本文是基于静力试验结果进行结构损伤识别，必要时可以与动测自振频率结合继续优化评估，为结构的加固维修提供参考。