钢管混凝土系杆拱吊索力的测试与调控

崔玉明，韩有龙，周新平

(1.中交隧道局第二工程有限公司，陕西 西安 710100；2.中建一局西北公司，陕西 西安 710067；3.中交第一公路勘察设计研究院有限公司，陕西 西安 710065)

0 引 言

对于系杆拱来说，吊索测试与控制是最关键、最复杂的工序，也是有别于其他型式拱桥的施工控制难点，究其原因，系杆拱吊索的张拉、拱肋和主梁的变形是耦合效应，主梁的变形影响着拱肋的内力和变形。吊索张拉的次序直接决定吊索的张拉次数和吊索索力的合理性，吊索索力的合理性又决定着系杆拱桥成桥后的内力分布状态以及桥梁的安全运营和使用寿命。所以，在设计系杆拱桥的过程中，需要通过大量的计算，分析系杆拱桥中各个构件的应力和变形，才能够得到一组合理的吊索力，使得在恒载作用下系杆拱桥的受力状态到达最优，实现吊索力优化全过程。

凌知民等假设了通过频率法测试吊索力的4种计算模型，并结合工程实例对实测数据进行了分析，提出了影响短索索力的关键参数[1]；陈强等针对短索索力的测试缺陷，考虑抗弯刚度对索力的影响，给出了计算长度的取值方法，提出索力计算修正系数[2]；王新定等通过静载试验测试了钢管混凝土系杆拱的索力性能[3]；张克波等研究了钢管混凝土轴心受压构件的承载力计算方法[4]；冯东明和刘灵勇等分别研究了基于频率法的吊索力测试分析技术[5-6]；盛兴旺等提出了确定系杆拱桥吊索力的刚性连续梁法的算法及系杆拱桥吊索千斤顶张拉力的确定方法[7-8]；李传习等提出了体外预应力索索力计算的新方法[9]；任伟新等提出了由基频计算拉索拉力的实用公式[10]。综上所述，学者们均从不同角度给出了不同桥型的索力测试及计算方法，由于多种原因造成成桥索力实际值与设计值之间存在差异，所以应该在施工过程中根据实际情况对索力进行优化控制分析[11-14]。

本文考虑吊杆索力的调控条件，通过建立单目标和组合目标的调控阈值，分析基于单目标和双目标控制的钢管混凝土系杆拱成桥吊杆索力值，并与设计值、实测值进行比较，确定该吊杆索力张拉过程的合理性及调控控制方法的可行性，并为后续的设计与控制提供指导。

1 工程背景

某异型钢管混凝土系杆拱桥如图1所示，其桥梁跨径长为60 m，拱轴线呈二次抛物线，拱矢高为12 m，拱肋选用等截面钢管混凝土结构，全桥由2片拱肋组成，拱顶设置1道H形横撑，拱肋下弦杆采用矩形截面，截面尺寸为1 500 mm×1 000 mm，拱肋钢管桁架高3.2 m。下弦杆拱肋钢管内部灌注微膨胀C50混凝土。主梁采用两箱三室的预应力混凝土箱梁，混凝土强度为C50级。截面高度为1.8 m，桥面宽度为37.5 m，每隔5 m设一道横隔梁，横隔梁通过吊杆与拱肋连接，全桥共11对吊索，吊索的设计强度为1 670 MPa。吊索的编号从拱脚到拱顶依次为1、2、3、4、5、6，调索顺序为2、4、6、5、3、1。主拱肋和主梁的最大变形设计值为20 mm，吊索力的设计值为1 800 kN。

图1 桥梁布置

2 调控计算

建立调控目标函数，即

(1)

式中:Δ为调控目标阈值，Fi为i节点控制变量。

取拱肋与主梁线形及主梁应力为调控变量，则有

(2)

式中:R为拱肋节点变形向量；Ri为拱肋第i节点的变形；G为主梁节点变形向量；Gi为主梁第i节点的变形；σ为主梁节点应力向量；σi为主梁第i节点的应力。

将式(2)代入式(1)，建立受索力影响的控制目标矩阵。

式中:S为拱肋节点变形向量；Si为第i根索的索力。

3 调控阈值

表1为系杆拱吊杆索力调控目标阈值的设定。由表1可知，假定3组优化调控计算序列分别为Δ1、Δ2和Δ3，第1组工况序列含有6组单目标工况，第2组工况序列含有4组单目标工况，第3组工况序列含有4组单目标工况。根据拱肋和主梁的最大设计变形值，设定拱肋和主梁的变形调控分级阈值，R-10、R-15、R-20分别表示拱肋的最大变形差为10、15、20 mm，G-10、G-15、G-20分别表示拱肋最大变形差为10、15、20 mm，max表示由拱肋和主梁变形分别控制得到的主梁最大应力值。

表1 目标阈值

4 吊索力调控

4.1 单目标控制

图2(a)为以拱肋变形作为调控目标的系杆拱桥成桥索力值。由图2(a)可知，当拱肋变形差为10 mm时，无法得到满足要求的索力值，所以选择拱肋变形差为15 mm和20 mm进行分析。当拱肋最大变形差控制在15 mm时，边吊索S1和S11的索力计算值与设计值的偏差为-11.5%，与实测值的偏差分别为-11.69%和-10.67%，其余吊索力计算值与设计值和实测值的偏差均在5%以内；当拱肋最大变形差控制在20 mm时，边吊索S1和S11的索力计算值与设计值的偏差为-15.0%，与实测值的偏差分别为-15.18%和-14.20%，其余吊索力值与设计值和实测值的偏差均在5%以内。

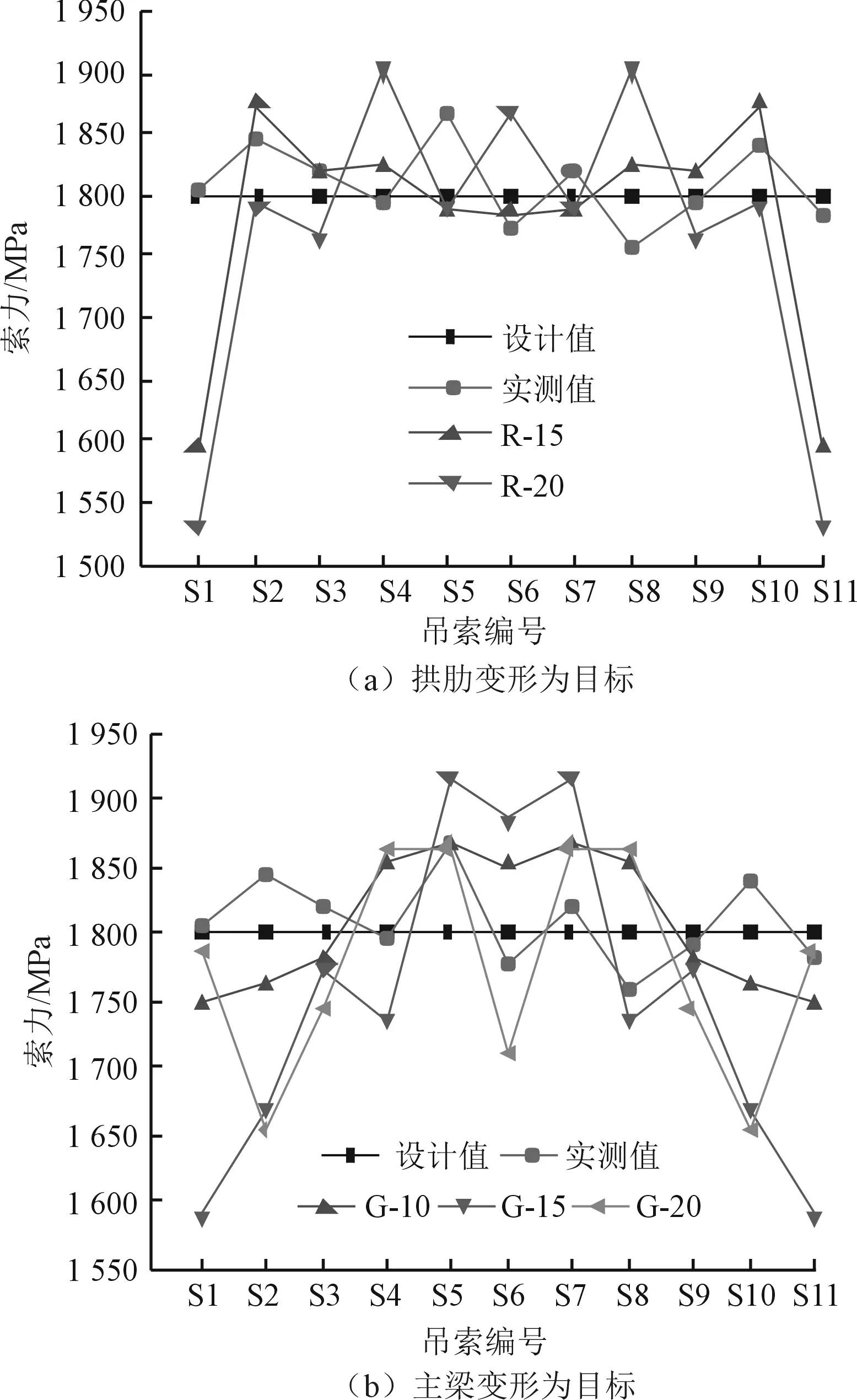
图2 单目标控制下的索力值

图2(b)为以主梁变形作为调控目标的系杆拱桥成桥索力值。由图2(b)可知：当主梁最大变形差控制在10 mm时，除吊索S8与实测值的偏差大于5%以外，其余吊索索力值与设计值和实测值的偏差均在5%以内；当主梁最大变形差控制在15 mm时，边吊索S1和S11的索力计算值与设计值的偏差为-11.72%，与实测值的偏差分别为-11.91%和-10.89%，吊索S2和S10的索力计算值与设计值的偏差为-7.28%，与实测值的偏差分别为-9.52%和-9.31%，吊索S5和S7的索力计算值与设计值的偏差为6.39%，与实测值的最大偏差为5.19%，大部分吊索力计算值与设计值和实测值的偏差均大于5%；当主梁的最大变形差控制在20 mm时，吊索S2和S10的索力计算值与设计值的偏差为-8.17%，与实测值的偏差分别为-10.40%和-10.18%，其余吊索力计算值与设计值和实测值的偏差均在5%以内。

图3为以拱肋变形和主梁变形作为调控目标的钢管混凝土系杆拱桥主梁的最大应力值。由图3可知，各控制目标下主梁的关键截面应力分布趋势保持一致，至梁端5 m和55 m的截面压应力较大，接近11 MPa，向跨中方向压应力逐渐减小，跨中20～40 m区域应力值基本一致，维持在5 MPa以内，因此后面的组合目标可设定主梁的压应力值为11 MPa。

图3 各控制目标的主梁最大应力值

总之，将拱肋变形15 mm和主梁变形10 mm作为控制目标时，成桥索力分布与设计值和实测值接近，且主梁应力未超过11 MPa，所以将此主梁应力值作为组合目标的控制阈值进行分析。

4.2 多目标控制

图4为组合调控目标下的钢管混凝土系杆拱桥成桥索力值分布。由图4可知：当以拱肋变形15 mm和主梁变形10 mm作为控制目标时，钢管混凝土系杆拱桥成桥索力值与设计值的最大偏差为3.33%，与实测值的最大偏差为4.31%，严格控制在5%以内；当以主梁变形10 mm和主梁桥跨方向全截面应力(S-11)同时作为控制目标时，吊索力的计算值与设计值和实测值偏差较大；当以拱肋变形15 mm和主梁桥跨方向全截面应力同时作为控制目标时，吊索力的计算值与设计值和实测值偏差较大，且分布不均匀。所以，应选取拱肋变形或主梁变形与主梁控制断面最大应力为目标，缩小其收敛范围，进一步调整索力值。

图4 多目标调控的索力值

5 结 语

(1)建立了调控目标函数，设定了调控目标阈值，通过拱肋和主梁变形及主梁应力提出了受索力影响的调控目标矩阵，分别对单目标和组合目标调控下的钢管混凝土系杆拱桥成桥索力进行了计算分析。

(2)对拱肋变形和主梁变形设定分级控制阈值，继而对钢管混凝土系杆拱桥成桥索力和主梁应力进行了计算，分析了不同级调控阈值的钢管混凝土系杆拱成桥索力分布状态，并将设计值和实测值进行了比较，选取合理的拱肋变形值作为调控目标得到的多组索力值分布均匀，选取合理的主梁变形值作为调控目标可得到一组均匀的索力值，可降其作为索力快速优化的调控目标值。

(3)基于单目标分级调控分析，优选了单目标控制的合理阈值，设定了拱肋和主梁变形及主梁应力的组合调控目标，对钢管混凝土系杆拱桥成桥索力进行了计算，结果与设计值和实测值接近，并分布均匀。本文结构可为类似桥梁的索力优化和控制提供参考。