多项式拟合法在旋盖机凸轮曲线设计中的研究与应用
2018-08-01佳何雪明何楷张
吴 佳何雪明何 楷张 荣
(1. 江苏省食品先进制造装备技术重点实验室,江苏 无锡 214122;2. 江南大学理学院,江苏 无锡 214122)
凸轮曲线从最早只能用于低速凸轮机构的等速曲线,到目前能够用于中、高速凸轮机构的标准多项式曲线、简谐凸轮曲线等已形成了一些系统论述[1-2]。王波波等[3]选取适当的设计变量,根据工程实际设计要求的凸轮机构参数,建立相应的优化模型,求出了符合实际情况的凸轮曲线。相较于简谐梯形组合凸轮曲线,多项式曲线只要取足够高的幂次数,高阶导数便总是连续的,因此可用于高速凸轮机构[4]。刘昌祺等[5]总结了数种多项式凸轮曲线的表达式,葛正浩等[6]给出了多项式凸轮曲线的通用表达式以及与各种边界条件相对应的解决办法。对于中低速凸轮机构,设计时进行运动学分析即可,但随着生产效率加快,凸轮机构的转速不断提高,仅仅分析运动学特性的方法渐渐失效,因此对于高速凸轮机构,在分析运动学特性的同时还需要关注其动力学特性。张策[7]对凸轮机构动力学方面的研究进行了分析与总结。田亚平等[8]建立了单自由度动力学模型来分析阻尼对凸轮动力学特性的影响,发现残余振幅会因阻尼的变大而慢慢衰减。高江红[9]建立了考虑输入轴速度波动的等效单自由度高速凸轮机构的动力学模型,对力封闭凸轮和形封闭凸轮的动力学特性进行了分析比较,为高速凸轮机构的合理设计提供了依据。
虽然凸轮曲线设计及动力学模拟在学术领域已有较为成熟的理论,但在实际生产过程中却缺乏科学的应用。目前中国多数从事液体食品包装的公司在设计旋盖机凸轮曲线时采用的方法是:将旋盖机完成相关动作时的各个关键点用直线相连,并在关键点连接处倒圆。这种方法将直接导致凸轮曲线仅满足速度连续,当凸轮高速运转时,由于存在柔性冲击,构件的动载荷比较大,旋盖机在现场工作时噪声大、易磨损,运行效率很低。因此,本研究拟采用多项式拟合法分别对凸轮曲线进行设计,以提高凸轮曲线的光顺性和连续性,然后对凸轮机构进行动力学仿真,最终达到降低旋盖机凸轮机构运行时的振动与噪声,提高机构运行精度。
1 多项式凸轮曲线表达方法
在利用多项式设计凸轮曲线时,经常会遇到局部位移控制条件过多的情况,运用多项式插值法会导致多项式幂次过高,不利于加工,此时运用多项式拟合法可以有效控制多项式幂次。
当凸轮处于升程期(或回程期)时,其控制条件为:在无因次时间Ti(i=0,1,……,m)处达到对应的从动件无因次位移Si(i=0,1,……,m)。此时可将问题转化为:存在m对数据(Ti,Si)(i=1,2,……,m),需用n次多项式来拟合这些点,多项式表达式为:
S=C0+C1T1+……+CnTn,
(1)
式中:
n≤m,选取合适的C0,C1,……,Cn,使得:

(2)
那么式(2)为最小二乘拟合多项式凸轮曲线。令
(3)
把式(3)对Ck求偏导数,得m+1个方程:
(4)
即
(5)
式(5)是关于C0,C1,……,Cn的线性方程,用矩阵表示为:

(6)
解出Ck(k=0,1,……,n),从而可得S表达式,即所设计凸轮曲线的多项式拟合表达。多项式拟合法能够有效解决局部位移控制条件过多的问题,但是拟合出来的凸轮曲线也会与位移控制点之间存在误差,因此在对n进行选取时要保证误差被控制在允许误差范围内。
2 多项式拟合法设计旋盖机凸轮曲线
2.1 凸轮曲线设计要求描述
现有一台旋盖机,单个旋盖头每小时旋盖1 800个,设计要求在提高转速的情况下,单个旋盖头每小时旋盖个数能够达到2 400个,且凸轮机构不会出现剧烈振动。凸轮从动件在相应角度到达对应的位移点,将这些位移点称为关键点,规定在关键点的设计允许误差为1 mm,其中出瓶位置点至 P1点(30°)和P2点(230°)至旋盖结束点为已定的两段水平位移,旋盖开始点至P2点也为既定的一段运动规律。由于现有的凸轮主要工作段在回程期,旋盖机需要在回程期完成主要的抓盖、进瓶和旋盖等动作,该段曲线设计的好坏直接影响了旋盖机的旋盖速度和旋盖质量,因此本文主要对回程期凸轮曲线进行设计,即主要对从P1点至旋盖开始点这段进行重新设计。旋盖机凸轮机构与凸轮模型见图1。
图1 旋盖机凸轮机构与凸轮模型
2.2 多项式拟合法设计凸轮曲线
从P1点至旋盖开始点共计6个关键点,依次为P1点、抓盖开始点、抓盖中心点、抓盖最低点、进瓶位置点、旋盖开始点,将时间T无因次化后得到各关键点的无因次位移。因为多项式拟合法缺少对边界导数条件的控制,所以不设定边界导数约束条件。多项式拟合法在应用时需要给定多项式的最后一项幂次数,为保证凸轮曲线的速度、加速度、跃度、跳度在回程期均连续,因此多项式的最高次幂最低必须为5次,本文取高速凸轮机构上常用的5次、6次和7次多项式进行拟合。
2.2.1 5次多项式拟合凸轮曲线 根据式(1),5次多项式拟合凸轮曲线位移函数可表示为:
S=C0+C1T+……+C5T5。
(7)
为更方便地控制凸轮曲线形状,另外插入局部控制点,结合约束条件,利用最小二乘法,得到5次多项式拟合的凸轮曲线见式(8)。
(8)
根据式(8)得到利用5次多项式拟合法设计出来的 P1点至旋盖开始点整体多项式凸轮曲线图谱,见图2。
在关键点的设计允许误差为1 mm,计算出各关键点的拟合误差见表1。从表1中可以看出,在抓盖开始点有最大的实际位移拟合误差为0.959 64 mm,小于设计允许误差1 mm,符合设计要求。

图2 5次多项式拟合凸轮曲线图谱
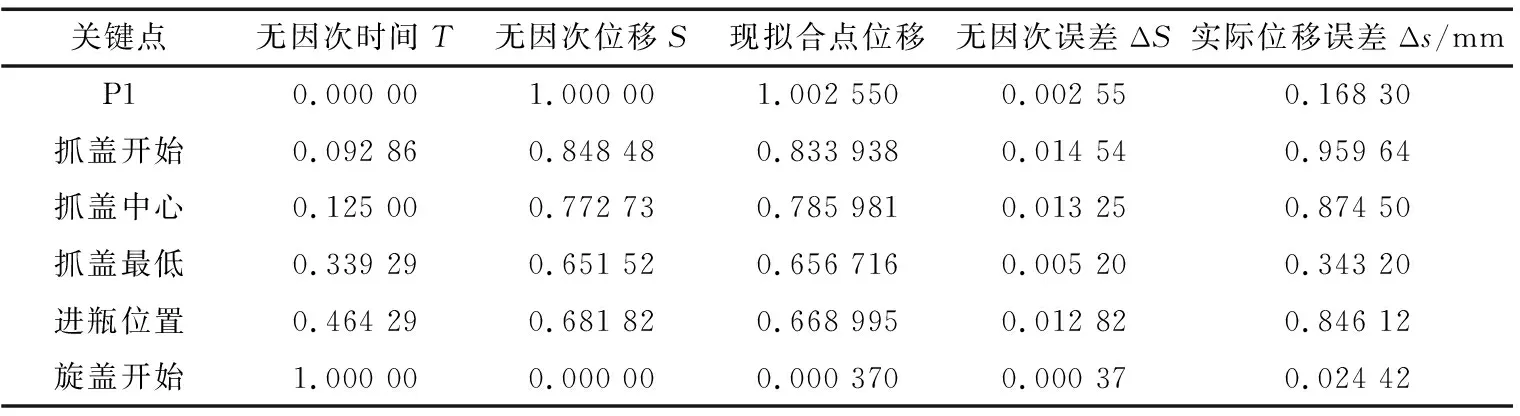
关键点无因次时间T无因次位移S现拟合点位移无因次误差ΔS实际位移误差Δs/mmP10.000 001.000 001.002 5500.002 550.168 30抓盖开始0.092 860.848 480.833 9380.014 540.959 64抓盖中心0.125 000.772 730.785 9810.013 250.874 50抓盖最低0.339 290.651 520.656 7160.005 200.343 20进瓶位置0.464 290.681 820.668 9950.012 820.846 12旋盖开始1.000 000.000 000.000 3700.000 370.024 42
2.2.2 6次多项式拟合凸轮曲线 仿照5次多项式拟合凸轮曲线的设计方法,调节控制点,可得到6次多项式拟合凸轮各特性曲线表达式,由表达式得到利用多项式拟合法设计出来的 P1 点至旋盖开始点6次多项式凸轮曲线位移图谱,见图3。
在关键点的设计允许误差为 1 mm,计算出各关键点的拟合误差见表2。
从表2中可以看出,在抓盖中心点最大的实际位移拟合误差为0.502 26 mm,小于设计允许误差1 mm,符合设计要求。
2.2.3 7次多项式拟合凸轮曲线 仿照5次多项式拟合凸轮曲线的设计方法,调节控制点,可得到7次多项式拟合凸轮各特性曲线表达式,由表达式得到利用多项式拟合法设计出来的P1点至旋盖开始点7次多项式凸轮曲线位移图谱,见图4。
在关键点的设计允许误差为 1 mm,计算出各关键点的拟合误差见表3。

表2 6次多项式关键点的拟合误差表
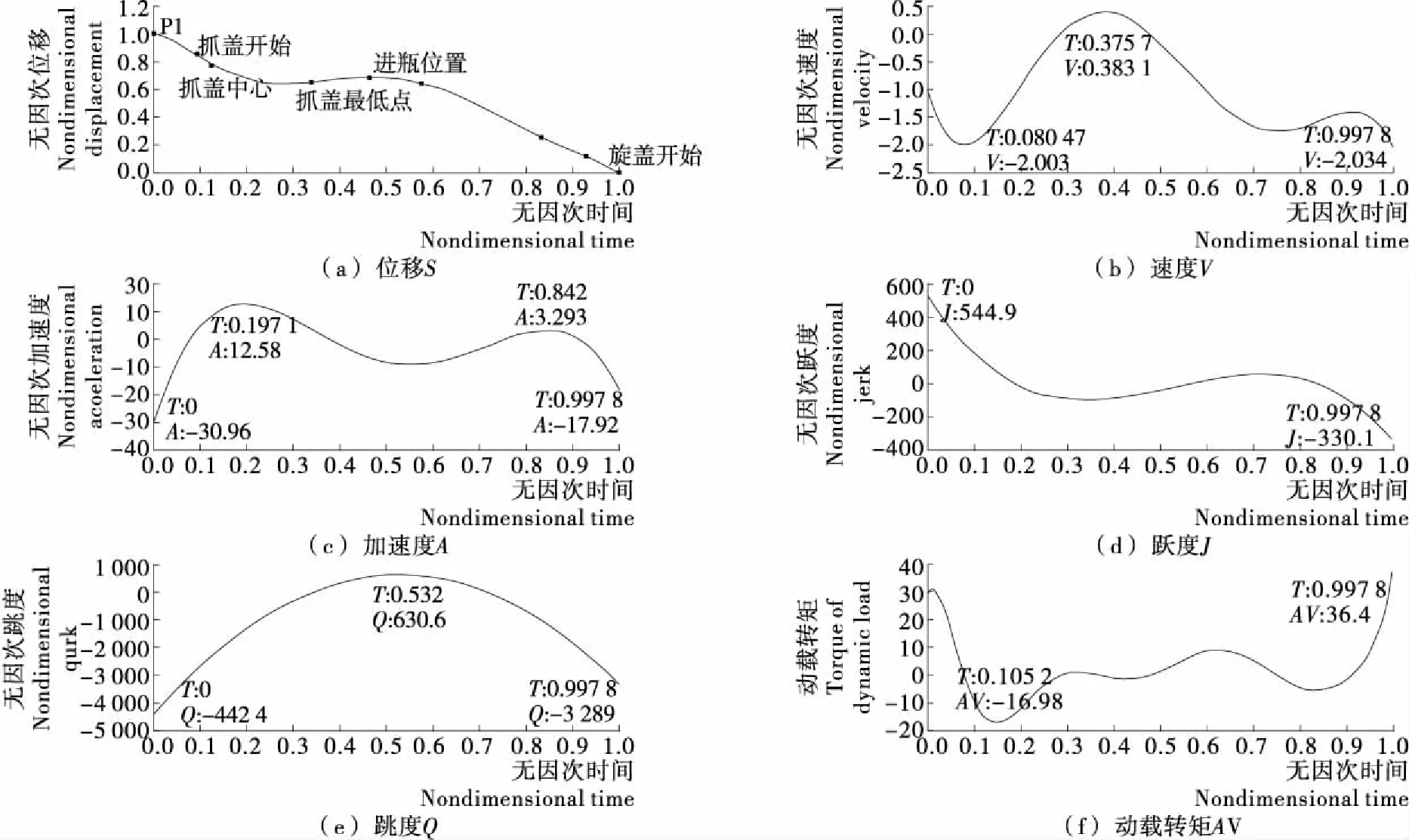
图3 6次多项式拟合凸轮曲线图谱
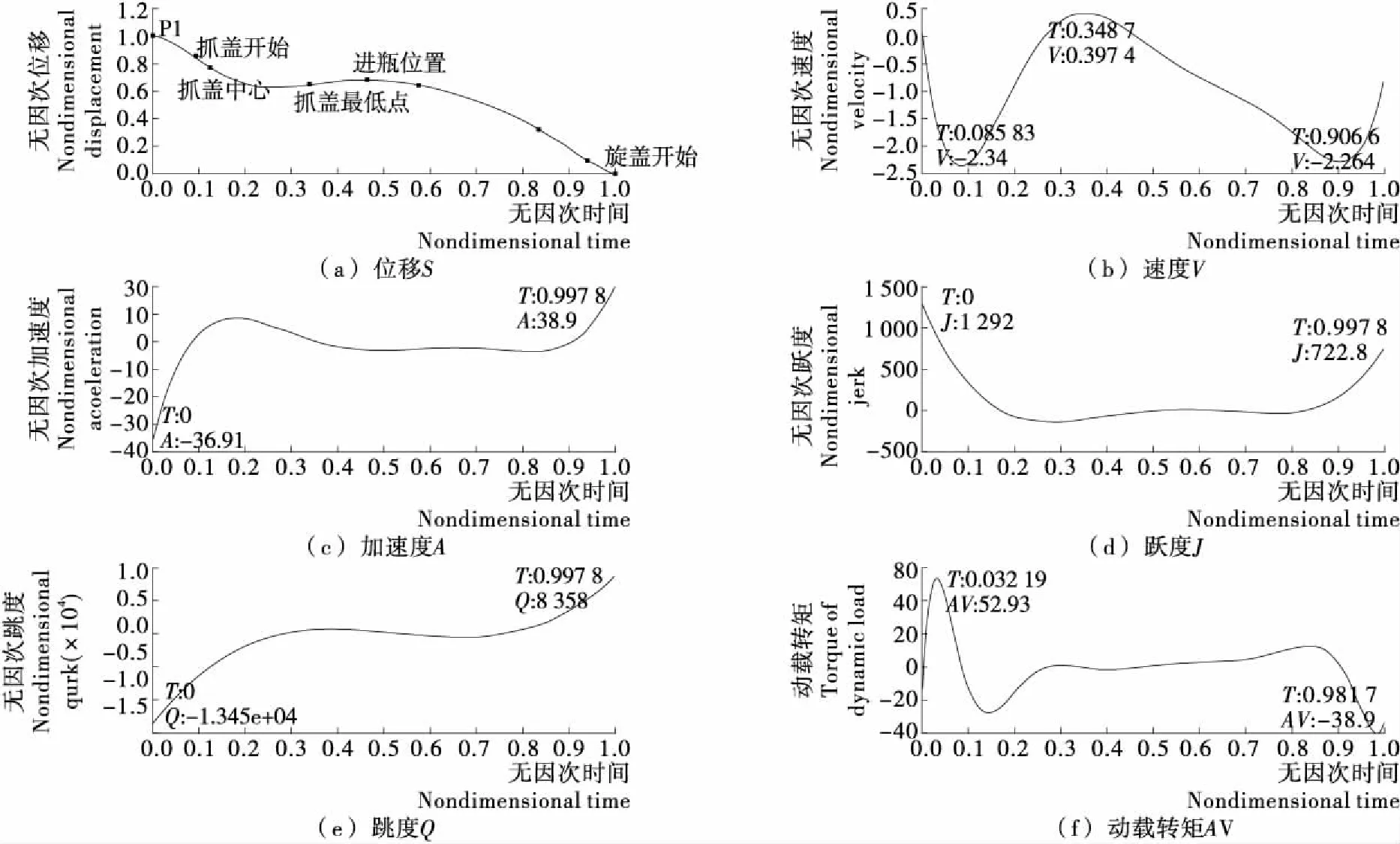
图4 7次多项式拟合凸轮曲线图谱

关键点无因次时间 T无因次位移 S现拟合点位移无因次误差ΔS实际位移误差Δs/mmP10.000 001.000 001.000 1800.000 180.011 88抓盖开始0.092 860.848 480.846 5060.001 970.130 02抓盖中心0.125 000.772 730.774 9600.002 230.147 18抓盖最低0.339 290.651 520.650 0890.001 430.094 38进瓶位置0.464 290.681 820.683 7960.001 980.130 68旋盖开始1.000 000.000 000.000 7010.000 700.046 20
从表3中可以看出,在抓盖中心点最大的实际位移拟合误差为0.147 18 mm,小于设计允许误差1 mm,符合设计要求。
由表1~3中可以看出,随着多项式的最后一项幂次数的增加,最大的实际位移拟合误差由5次多项式拟合的0.959 64 mm 减少到7次多项式的0.147 18 mm,其他关键点的实际位移拟合误差也相继减少,可以看出增加最后一项幂次数,多项式拟合精度更高。为了更直观地分析凸轮曲线特性参数的变化,将5次、6次、7次多项式拟合凸轮曲线特性参数集中加以比较,见表4。
表4 5次、6次、7次多项式拟合凸轮曲线特性参数对比表
Table 4 Five-power, six-power and seven-power polynomial fitting cam curve characteristic parameter comparison table
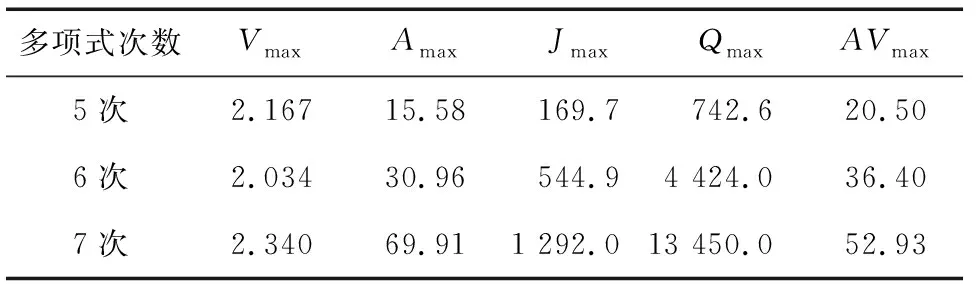
多项式次数VmaxAmaxJmaxQmaxAVmax5次2.16715.58169.7742.620.506次2.03430.96544.94 424.036.407次2.34069.911 292.013 450.052.93
从表4中可以看出,在各特性参数中,6次多项式的最大速度Vmax最小,为2.034,其他特性参数Amax、Jmax、Qmax和AVmax均是5次多项式最优。而7次多项式的各种特性值在3种多项式曲线中均是最高的,因此性能较差。而且5次多项式的最大速度为2.167,与6次多项式相差不大,并且在高速凸轮机构中,最大加速度Amax的重要性优于最大速度Vmax,而5次多项式的最大加速度为15.58,只有6次多项式的最大加速度(30.96)的50%左右,因此可以看出这3种多项式中,5次多项式拟合的凸轮曲线综合性能最优。同时,多项式拟合法可以有效解决整体多项式插值法不能控制位移局部形状的问题以及分段多项式插值法位移高阶导数会出现尖点及突变、曲线衔接不光滑的问题。
3 旋盖机凸轮机构动力学分析
3.1 原凸轮机构动力学分析
为了验证新设计的凸轮曲线性能,需要先将原旋盖机凸轮机构模型进行动力学仿真分析,如图5所示,将原凸轮机构模型分为5部分,即凸轮中心轴、凸轮、凸轮从动件、从动件上滚子、从动件下滚子,将凸轮机构模型导入ADAMS软件中,对各零部件添加约束与驱动。
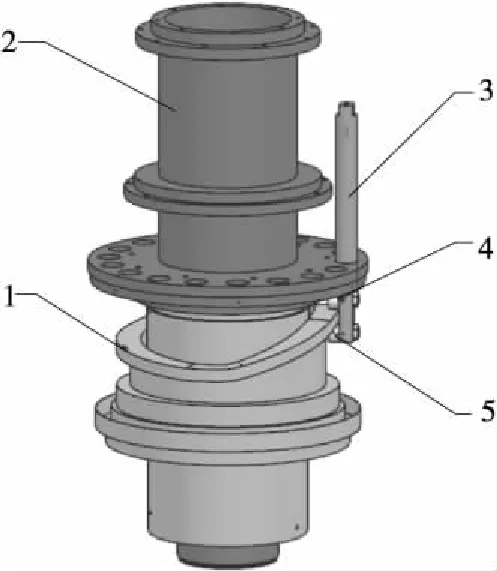
1. 凸轮 2. 凸轮中心轴 3. 凸轮从动件 4. 凸轮上滚子 5. 凸轮下滚子
图5 凸轮机构导入ADMAS的三维模型
Figure 5 3D model of cam mechanism imported into ADMAS
设置完仿真条件后开始进行动力学仿真分析,得到结果见图6。
由于原有的凸轮曲线是将各关键点以直线连接,并在关键点处倒圆,因此仅仅能保证凸轮曲线的速度连续,但加速度容易在关键点处发生突变。分析图6可知,加速度曲线在凸轮机构主要工作段即回程有几处明显的突变,这是比较符合实际情况的,因为该凸轮机构升程期不是主要工作段,对旋盖机影响比较小,因此主要对P1点至旋盖开始点段动力学仿真结果进行分析。为了消除量纲的影响,将P1点至旋盖开始点段位移、速度和加速度曲线无因次化,得到P1点至旋盖开始点段无因次动力学仿真曲线见图7。
分析图7可知,原凸轮机构的动力学仿真速度曲线基本连续,速度绝对值最大为5.777,而加速度在整个周期内均不连续,且多个地方存在冲击,最大加速度达到了4.393×104,高速状态下,很容易导致凸轮机构磨损、振动和疲劳破坏,随着振动的加剧,从动件的实际运动曲线必将偏离理论曲线,发生动态运动误差。
3.2 多项式拟合凸轮动力学分析
为了验证新设计的凸轮曲线性能,分别将5次、6次和7次多项式拟合凸轮曲线转换成凸轮轮廓线并建出凸轮机构模型,导入 ADAMS软件并仿照原凸轮机构动力学分析方法,分别得到3种多项式凸轮曲线对应凸轮机构在P1点至旋盖开始点段的无因次动力学仿真曲线,与原凸轮动力学仿真曲线进行比较,结果见图8。
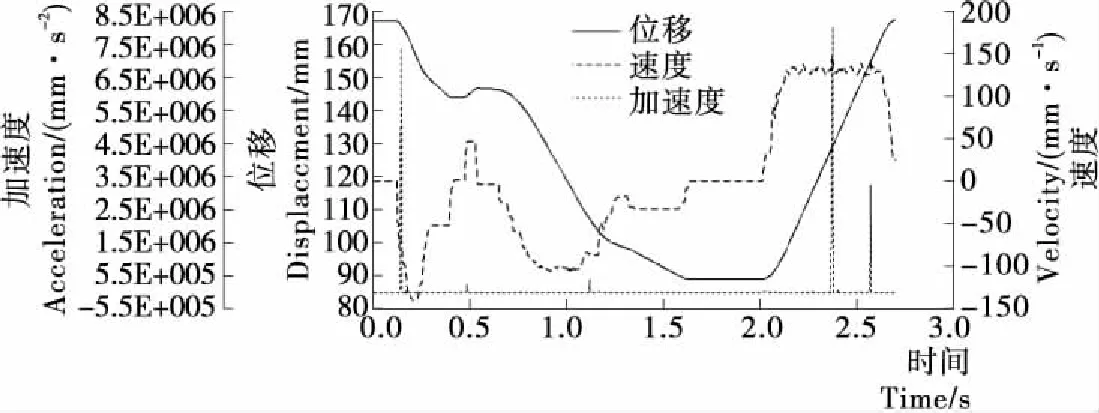
图6 原凸轮动力学仿真结果
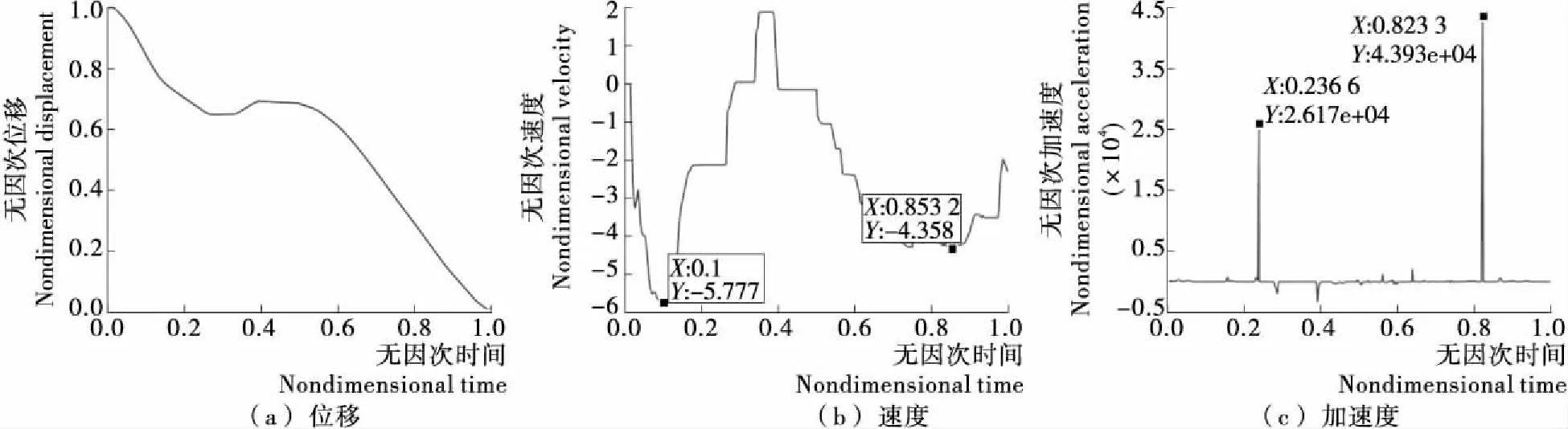
图7 P1点至旋盖开始点段无因次动力学仿真曲线图谱
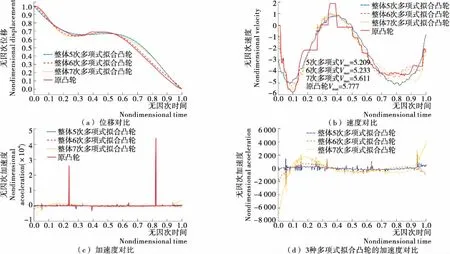
图8 多项式拟合凸轮和原凸轮动力学分析对比
分析图8可以发现,3种多项式拟合凸轮的位移曲线很明显比原凸轮的位移曲线更加光顺,在T=0.1附近,所有速度曲线方向为负,速度急剧增大,其中原凸轮速度曲线变化最大,仿真速度最大值达 5.77;对于仿真加速度曲线,原凸轮的加速度变化也远远大于其他曲线,因此可知多项式拟合法设计凸轮曲线是有效的。由图8(d)可知,在3种加速度曲线中,整体5次多项式拟合凸轮运行最平稳,波动最小,整体 7次多项式拟合凸轮运行时波动最大,与理论加速度曲线的分析是一致的。
由于阻尼和间隙等因素的影响,3条多项式的仿真速度最大值都远大于理论速度,见表5。6次多项式拟合凸轮的理论速度最大值大于5次多项式的,但是仿真值却是5次多项式拟合凸轮略优于6次多项式的,再因为5次多项式拟合凸轮加速度曲线更平稳,因此可以判断5次多项式拟合凸轮曲线的综合性能优于其他2种曲线。
表5 多项式拟合凸轮理论与仿真速度最大值对比
Figure 5 The comparison of the maximum speed of the polynomial fitting cam theory and simulation
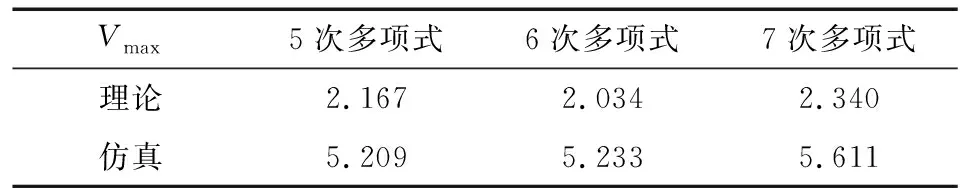
Vmax5次多项式6次多项式7次多项式理论2.1672.0342.340仿真5.2095.2335.611
4 结论
(1) 经过多项式拟合后的凸轮曲线各项特性参数与原凸轮相比均有所改善。首先,就凸轮运动学性能来说,6次多项式的最大速度Vmax最小(2.034),5次多项式次之(2.167),其他特性参数Amax、Jmax、Qmax和AVmax均是5次多项式最优,7次多项式的各种特性值在3种多项式曲线中均最高,因此运动学性能较差;虽然随着幂次的增加,最大的实际位移拟合误差由5次多项式的0.959 64 mm减小到了7次多项式的0.147 18 mm,但5次多项式拟合误差仍能满足误差小于1 mm的设计要求。其次,经过多项式拟合设计的凸轮曲线在动力学性能上也得到了提高,位移、速度曲线较原凸轮变得更加光顺,加速度未再出现明显的突变现象,对比3种多项式拟合而构造的凸轮,以5次多项式拟合的凸轮曲线动力学综合性能最优。因此,针对该种旋盖机凸轮机构,采用5次多项式拟合凸轮曲线的设计方法最合适。
(2) 本研究所采用的多项式拟合凸轮曲线设计方法,相比于企业用直线连接关键点并倒圆的设计方法,极大地提高了曲线的连续性,曲线由原本的G1连续升至G2、G3,甚至是G4,这将有效提高凸轮机构的动力学性能,减少机构振动,从而使旋盖机在提高转速的情况下也能平稳运行。
(3) 本研究为凸轮曲线设计提供了比较灵活的设计方法,研究了凸轮曲线对凸轮机构动力学特性的影响,所建立的动力学模型虽然精度已足够,但仍不够精细,后期可以将间隙的影响考虑其中,进一步深入研究凸轮曲线对凸轮机构动力学的影响。
