基于RI-ALE-MUSIC的舰船地震波时频检测

马剑飞， 颜 冰, 陈春行， 王兆仁

(海军工程大学 兵器工程系,武汉 430033)

舰船地震波是指舰船航行时所产生的船体振动噪声和舰船辐射噪声的低频部分，耦合到海底并以弹性介质波的形式在海底传播。舰船地震波场作为一种新型的舰船物理场，其应用研究的重要意义就在于利用舰船地震波独特的频率特性和传播特性来弥补常规水声换能器在水中目标探测中的不足，有力地提高水中兵器被动探测舰船目标的能力[1]。

舰船地震波的频率特性主要取决于舰船低频辐射声场，其中舰船辐射噪声主要是由舰船的机械噪声、螺旋桨噪声和水动力噪声组成。一般来说，目标船的辐射噪声，不仅会产生宽带的连续谱，也会产生具有窄带的线谱成分。其中线谱能量稳定，适合用来对舰船目标进行检测[2]。

1 算法原理

为了解决舰船地震波信号时频局部化的问题，可以给傅里叶变换加一个滑动的“时间窗”，对信号进行时频分析。时频分析法主要研究频谱时变的确定性信号和非平稳随机信号(统称为非平稳信号)，短时傅里叶变换(STFT)虽然在一定程度上克服了傅里叶变换不具有的局部分析能力的缺陷，但其实质上只是具有单一分辨率的时频分析方式。若要改变分辨率，就必须重新选择窗函数[3]。

为了改变STFT的不足，基于经典的MUSIC功率谱算法(C-MUSIC)，提出一种自适应线谱增强和MUSIC组合的算法(ALE-MUSIC)，并据此提出了一种相对强度时频检测算法(Relative Intensity ALE-MUSIC，RI-ALE-MUSIC)。首先采用滑动窗函数分段截取数据，然后进行ALE-MUSIC处理和相对强度处理，之后进行阈值判定，最终得到检测时频图，算法流程见图1。

1.1 自适应谱线增强

对于含有固定频率的信号，常采用自适应谱线增强器(Adaptive Line Enhancer，ALE)提取信号中的线谱成分，其核心是自适应滤波器，将信号经过相关延迟输入滤波器，作为参考信号和原始信号相比较得到误差信号输出，误差信号按照最优准则调整滤波器参数，使得输出信号达到最优[4-6]。图2是其原理示意图。

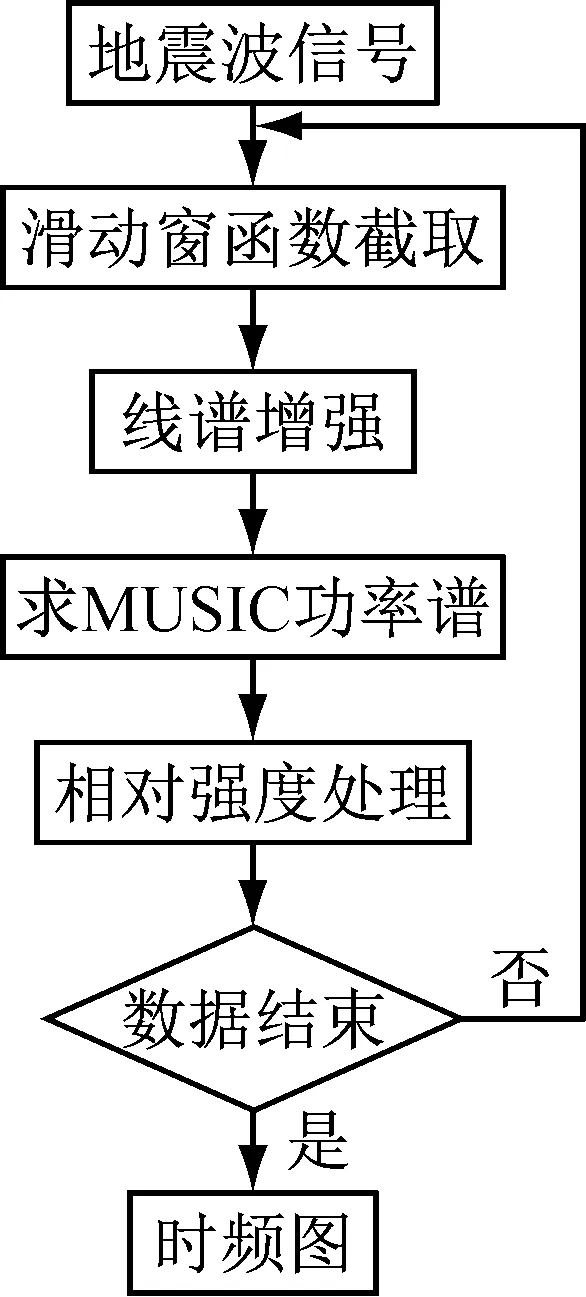
图1 算法流程图

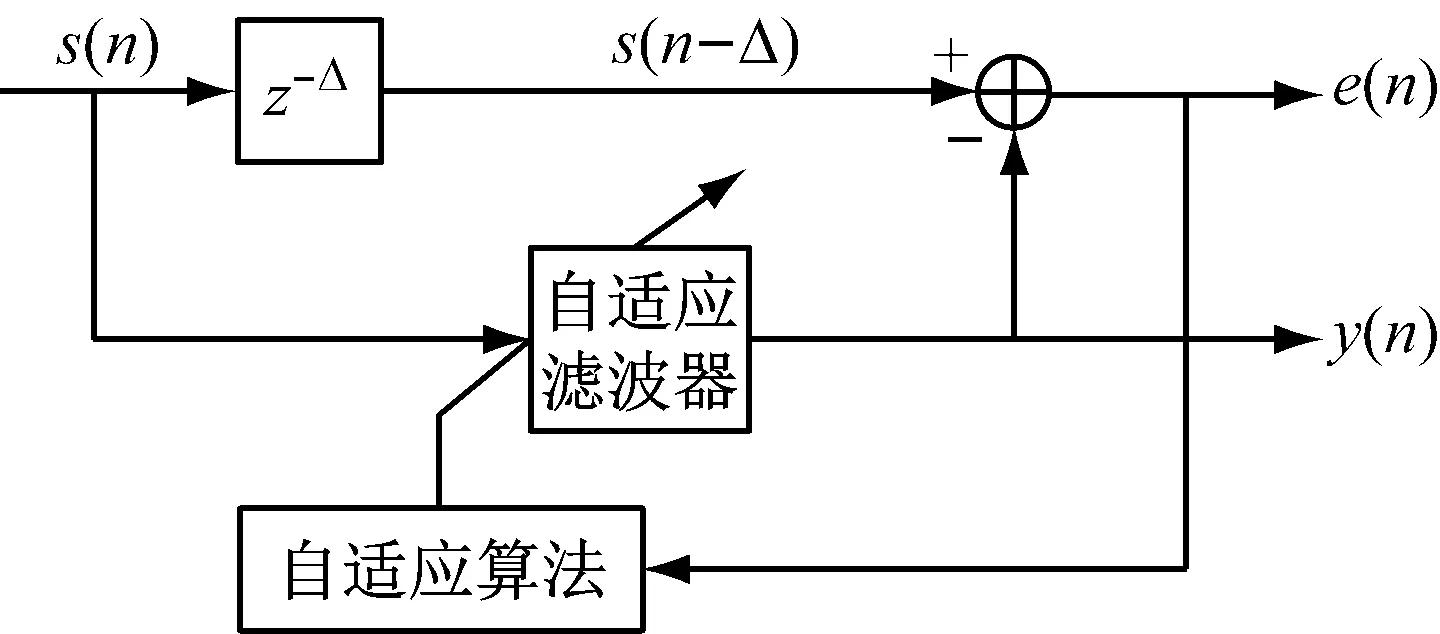
图2 自适应谱线增强器

选用LMS准则对系统参数进行估计，迭代公式为

d=[ones(1,Δ),s(1:N-Δ)]

(1)

x(n)=d(n:n+Δ)

(2)

y(n)=w(n)xT(n)

(3)

e(n)=s(n)-w(n)xT(n)

(4)

w(n+1)=w(n)+2μe(n)x(n)

(5)

w(0)=[1,1,1,1]

(6)

式中：s为采集到的舰船地震波信号；y是输出的线谱增强信号；e是输入输出信号的误差；μ是步长因子；w(n)是抽头权向量；x(n)是抽头输入向量。

1.2 MUSIC功率密度谱估计

一般来说，基于信号模型理论的谱估计方法只适应于具有连续谱的规则过程，而对于离散谱的可预测过程，若使用参数模型估计方法，则会导致谱峰的平滑。离散谱估计主要是频率点的估计，常采用特征分解技术[7]。

功率谱估计(Multiple Signal Classification，MUSIC)是基于矩阵特征分解的一种功率谱估计的非参数方法[8]，将自相关矩阵的信息空间分为信号子空间和噪声子空间,再利用信号向量和噪声子空间的正交性来完成频域功率谱估计。MUSIC法功率谱估计的公式为

(7)

e(f)=[1,exp(j2πf),…,exp(j2πf(m-1))]T

(8)

式中:f是复正弦波频率；N是特征向量的维数；Vk是输入信号的相关矩阵的k阶特征向量；M是信号子空间的维数即分解的复正弦信号的个数。

2 信号处理

利用设计的地震波探测系统(MEMS传感器)在汉江江堤进行测试。实验测量时，无明显工业干扰源，测量目标为江上的货运船只，其航速约为10节，航向保持不变。

2.1 时域和频域分析

如图3所示是系统采集到的Z轴加速度信号，采样时长500 s，系统的采样频率为460 Hz，信号的起始点距传感器-1 160 m(负号表示舰船未通过传感器)，信号的终点距传感器1 340 m。可以看出，在232 s时信号达到峰值，信号明显的波形起伏时间约为20 s，如果简单地利用地震波信号时域包络特征识别舰船目标，其探测距离非常短，所以考虑时频域线谱检测的方式来探测舰船目标。

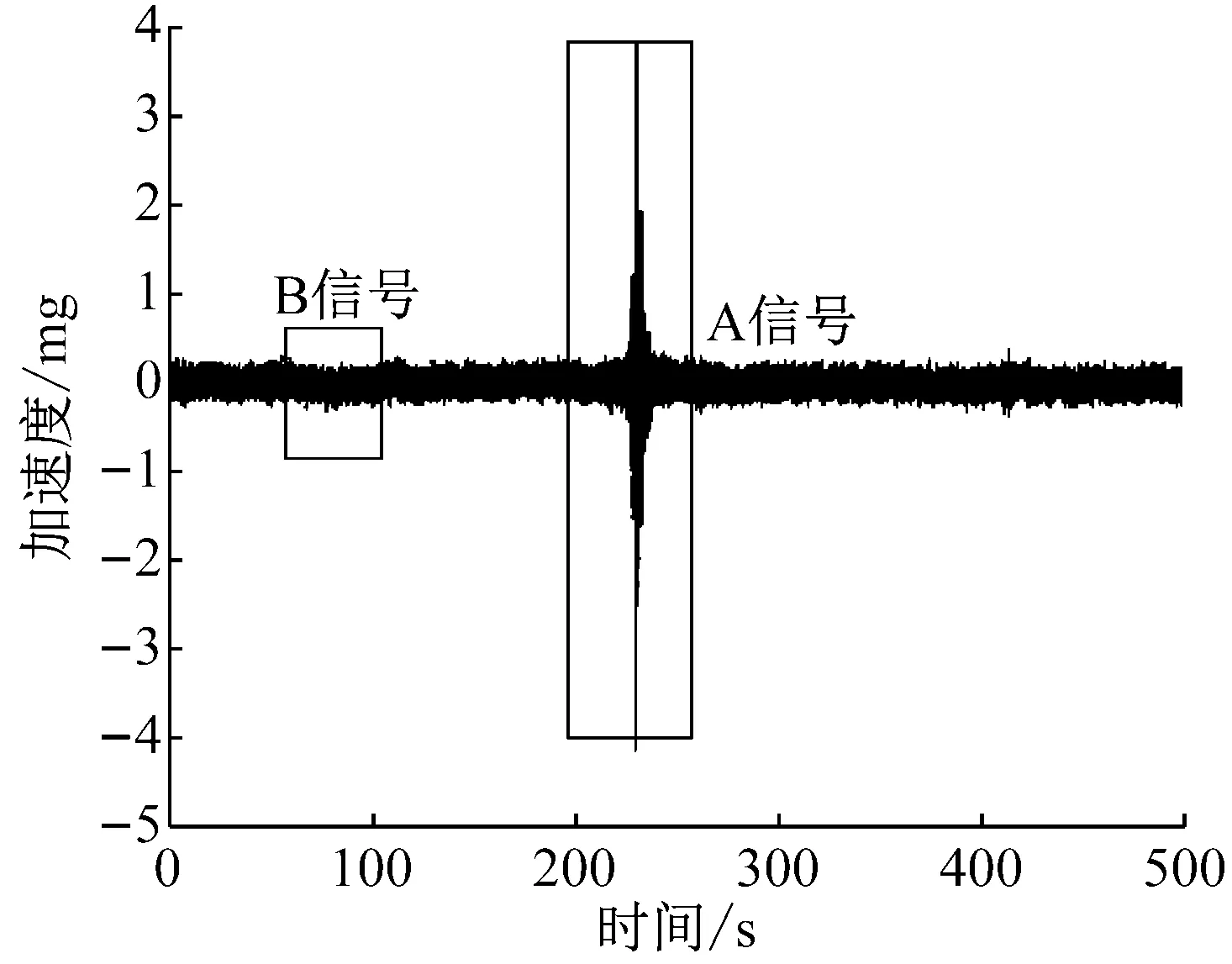
图3 舰船地震波时域信号

从图3中截取的一段舰船距离传感器约-48～63 m有明显起伏的波形，记为A信号(信噪比约为25.7 dB);截取的一段舰船距离传感器约-627～-534 m的无明显起伏的波形，记为B信号(信噪比约为-12.3 dB)。分别对A信号和B信号做FFT变换，得到所对应的频域波形如图4(a)和图4(b)所示。通过对比可以发现，A信号的频域幅值整体要大于B信号的频域幅值，且A信号在15 Hz的频点处有明显的线谱，而B信号无明显线谱。主要原因有两方面：①A信号是在舰船距传感器距离较远处测得的信号，其线谱分量信号较弱；②FFT变换对频谱分辨率不高。基于此，考虑采用MUSIC功率谱法对离散谱的频点进行估计。

图4(c)中的黑色实线是A信号C-MUSIC功率谱，图4(d)中的黑色实线是B信号C-MUSIC功率谱,可以看出C-MUSUC算法可以有效识别信号中的A信号和B信号的线谱分量，即可以识别FFT变换所不能识别的B信号15 Hz线谱分量。

对ALE中的Δ取值1～15进行分析，经运算检验Δ值为3时，对实测地震波的线谱增强后效果最好。由于失调系数正比于步长因子，而平均时间常数与步长因子成反比，综合之后取μ值为0.01。

在图4(c)、图4(d)中，灰色虚线代表ALE-MUSIC功率谱，与其中的黑色实线对比可以发现，自适应线谱增强算法明显地增强了功率谱图中的线谱分量。如图5所示，当舰船距离再增加时，C-MUSIC识别谱线的能力变得很差，而ALE-MUSIC依然可以有效识别谱线。

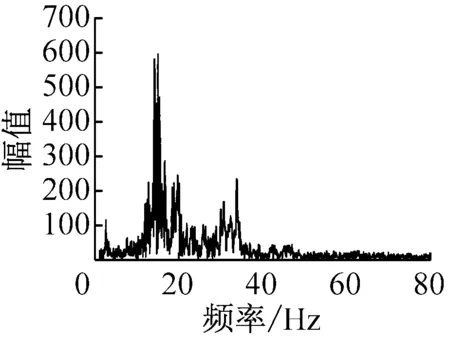
(a) A信号FFT频域波形

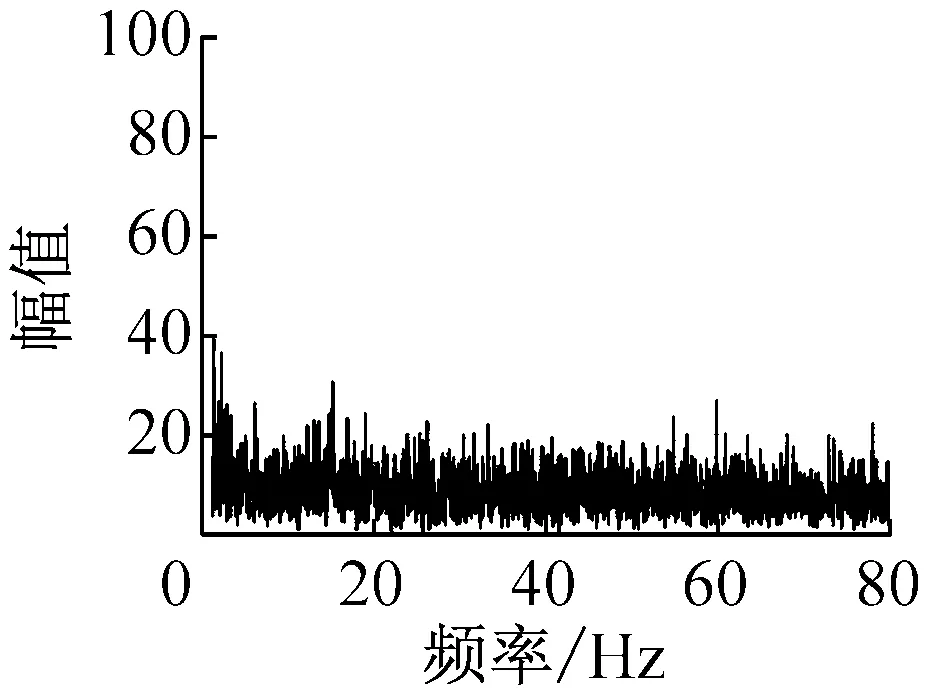
(b) B信号FFT频域波形

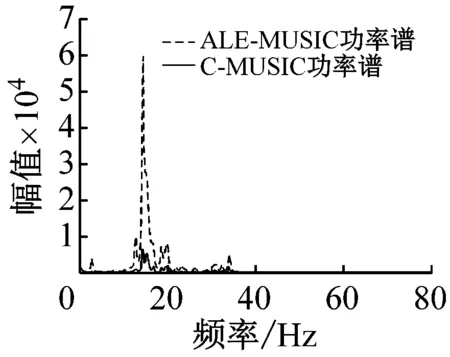
(c) A信号MUSIC功率谱对比

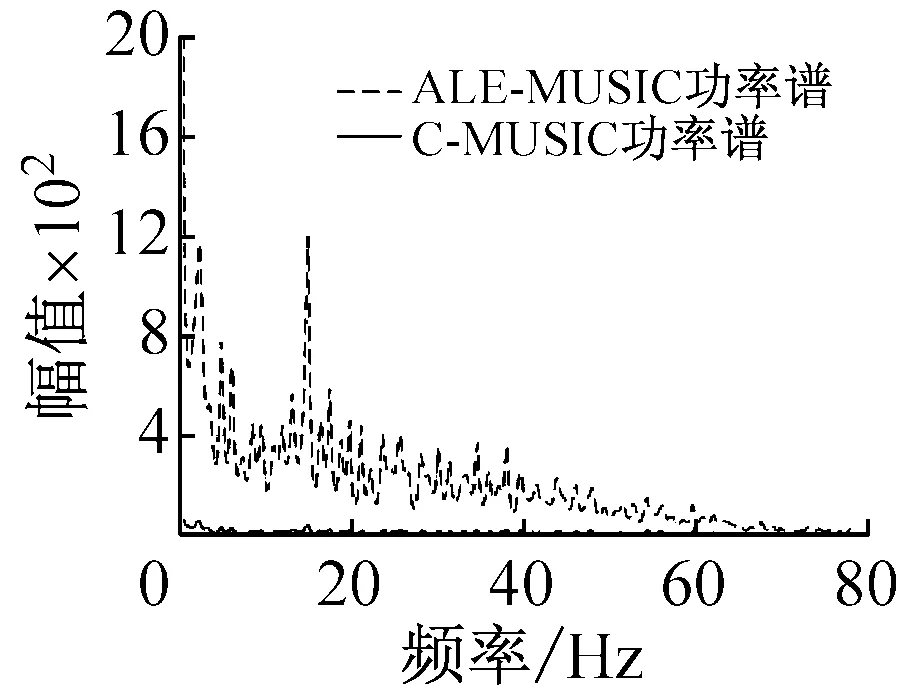
(d) B信号MUSIC功率谱对比

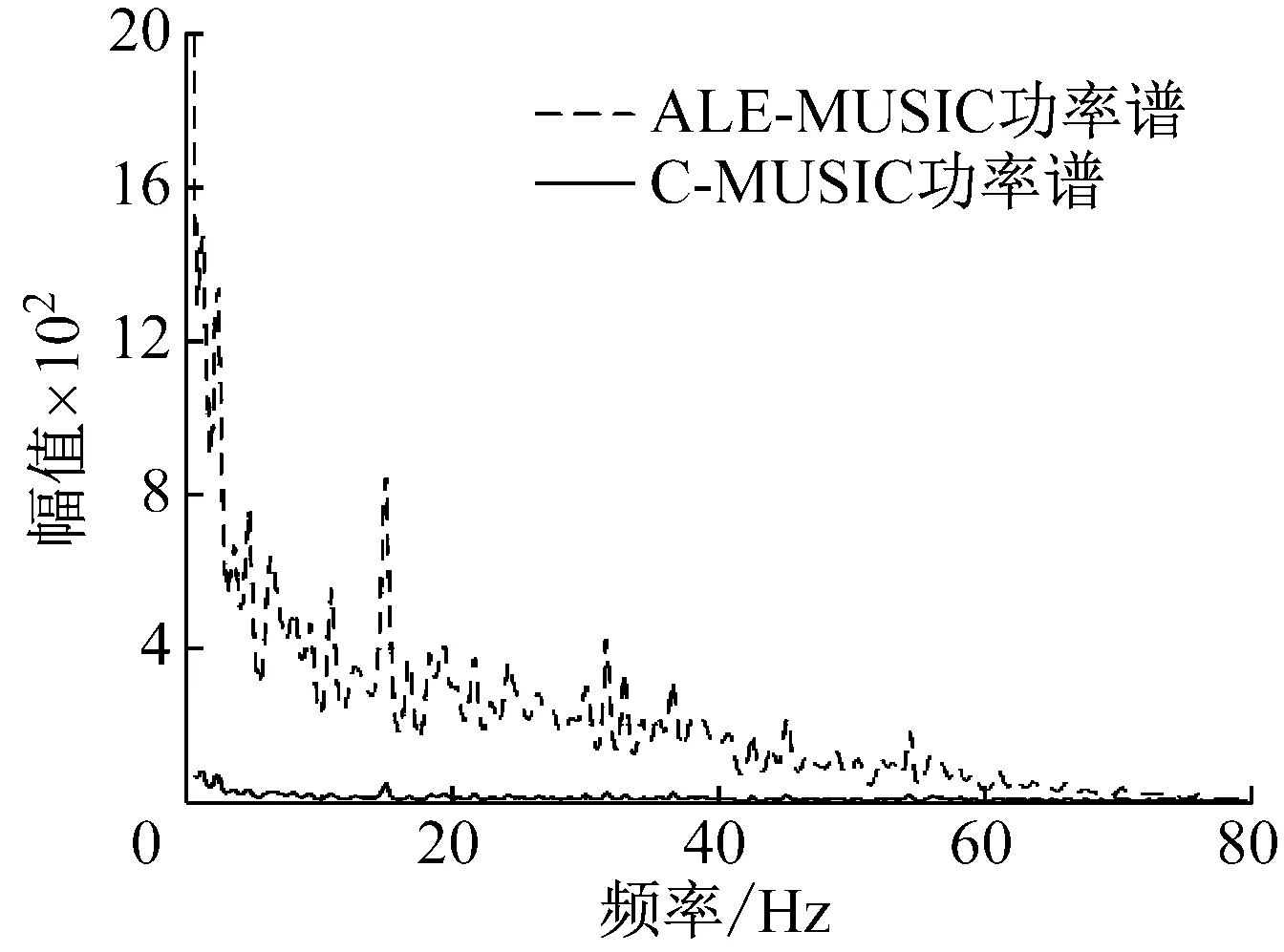
图5 远距离信号MUSIC功率谱对比

舰船的螺旋桨噪声由空化噪声和旋转声组成，其中旋转声是由在周向变化的尾流中工作的螺旋桨产生的推力的振荡分量所引起[9-10], 旋转声又分为轴频噪声和叶频噪声

(9)

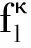
2.2 RI-ALE-MUSIC时频处理

频域处理不具有时间和频率的“定位”功能，因此无法用作对舰船目标的实时检测，为了解决舰船地震波信号实时检测的问题，给信号加一个滑动的“时间窗”函数进行时频处理[11]。

图6是使用MATLAB中的spectrum函数得到的时频图，即STFT的变换结果(运算时采用FFT变换处理Hamming截取的数据)，可以看出在232 s前后出现了一段持续时间约48 s(208～256 s)，频率为15 Hz谱线，且谱线能量有明显的弱—强—弱的变化，即代表了舰船的驶近和远离。与图1中的波形的强弱变换存在一致性，但其探测距离仍然很近，达不到探测的指标要求。

由于短时傅里叶变换不能很好地识别远距离舰船信号的线谱，所以采用RI-ALE-MUSIC算法进行时频处理。式(10)和式(11)是推导的表达式

(10)

式中：Pmusic(t,f)代表时频图中t时刻；f频点的能量；N0是数据总长度；N是特征向量的维数；Vk是输入信号的相关矩阵的k阶特征向量，M是分解的复正弦信号的个数。对Pmusic(t,f)做相对值值相对处理

(11)

式中：Rmusic(t,f)表示在t时刻，f频点的能量相对于t时刻整个频域能量的比值。

图6 短时傅里叶变换时频图

如图7所示，选取6 000点、重叠率为50%的矩形窗截取数据，自适应线谱增强后求取相对MUSIC功率谱(N=6 000，M=1 000)，以时间点为横轴坐标，以频率点为纵轴坐标，将各段功率谱结合起来得到地震波信号的时频图，即反映舰船的通过特性。

图7 RI-ALE-MUSIC时频图

在图7中15 Hz的谱线持续时间为290 s(115～432 s)。由于在232 s时传感器正好在舰船正横方向上，通过简单计算可知STFT的预警时间为24 s，RI-ALE-MUSIC时频算法的预警时间为117 s。所以采用RI-ALE-MUSIC时频算法相比于使用STFT算法，大大提高了对舰船目标的探测距离。

2.3 RI-ALE-MUSIC时频检测

设定阈值识别舰船目标是探测的一种常用方法，当MUSIC相对谱强度满足式(12)时

Rmusic(t,f)>λ

(12)

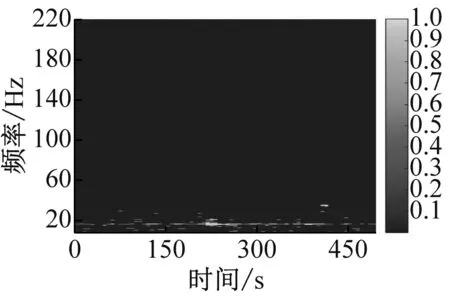
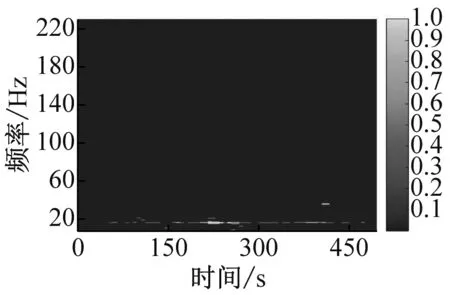
令Rmusic(t,f)=1，即对信号进行二值化处理，式中λ为判决阈值。由于M取值为1 000，所以某时刻各个频点相对频谱分量应为2/M，即为0.002。目标舰船位于系统的探测范围时，信号在特定的频点处的能量会增强为原来能量的k倍。当k取值10、20、30时，对应阈值λ分别取值0.02、0.03、0.04，采用相对强度ALE-MUSIC时频检测算法的处理结果如图8(a)、8(b)、8(c)所示。

(a) λ值为0.02的检测结果

(b) λ值为0.03的检测结果

(c) λ值为0.04的检测结果

图中在某时刻15 Hz频点处的亮点表示此时已检测到舰船目标信号，而15 Hz频点处的暗点代表此时未检测到舰船目标信号。可以看到在该频点亮点之间还存在一些暗点，这是由地震波信号(低频信号)不同路径传播产生干涉现象所致。

对比不同阈值的结果易知，随着阈值的增加，探测的距离会降低，但阈值过低，相应地其谱线结构就会变得杂乱，也就意味着虚警概率会升高。虚警率过高会导致探测系统的功耗增大，也容易导致系统误判，而探测距离太近又不能发挥地震波探测系统探测距离远的优势，所以设计系统时应综合考虑探测距离和虚警概率的关系。通过对比可以发现，对于本型测量船λ值取0.03效果最好。

3 结 论

研究了一种以C-MUSIC算法为基础的RI-ALE-MUSIC时频检测算法，并对实测舰船地震波信号进行分析，结果表明该算法即使在信噪比为-12.3 dB的情况下仍然可以有效检测到舰船目标，预警探测距离相比于采用时域包络的探测提高了10倍～20倍(通过预警时间估算得到)。

本文分析的数据是在汉江的江堤测得，传感器距离舰船最近时也有50 m的距离，所以地震波信号传播距离相对较远且在江底和江堤的耦合过程中衰减较大。此外，货船吨位小、航速低即信源强度较小，也是测量信号强度低的重要原因。实际应用过程中，将探测系统置于海底测量海面舰船，其探测距离会进一步加大。